Chapter 12

TWO CARD TRICKS

A mathematician is a conjurer who gives away his secrets.

John Conway

The bewilderment that accompanies a well-performed, good card trick relies greatly on the expertise of the conjurer—the ability to misdirect, to manipulate both cards and observer—and sometimes an underlying principle which is surprising in itself. We are interested in two such principles, both of which are the basis of numerous effects and both of which were discovered by academics.

The Kruskal Principle

The second chapter of Genesis continues the story of the creation of Heaven and Earth and begins (King James Version):

Thus the heavens and the earth were finished and all the host of them And on the seventh day God ended his work which he had made and he rested on the seventh day from all his work which he had made And God blessed the seventh day and sanctified it because that in it he had rested from all his work which God created and made These are the generations of the heavens and of the earth when they were created in the day that the LORD God made the earth and the heavens And every plant of the field before it was in the earth and every herb of the field before it grew for the LORD God had not caused it to rain upon the earth and there was not a man to till the ground But there went up a mist from the earth and watered the whole face of the ground And the LORD God formed man of the dust of the ground and breathed into his nostrils the breath of life and man became a living soul . . .

and we can use the text to engage in a little ‘Bible code’ numerology.

Start at the first word (Thus) and count along one word for each of its four letters (to reach the); then count along one word for each of its letters (to reach finished) and continue the process; eventually the bold and underlined word God will be reached. Coincidence perhaps? Now start at any word in (say) the first six lines of the text and the same will happen: the sequence will reach the same occurrence of the word God. In fact, if we start at any word up to and including the of the same thing will happen. That all paths lead to God is comforting, but is this more than coincidence? Actually, a nonmystical explanation is perfectly simple: the chains of words generated in the above manner all have an instance of the word earth as a first common link, and of course from that point on the chains are identical and since one of them has God as a link, all must do so. The passage is repeated below with that first common link and all subsequent links emboldened:

Thus the heavens and the earth were finished and all the host of them And on the seventh day God ended his work which he had made and he rested on the seventh day from all his work which he had made And God blessed the seventh day and sanctified it because that in it he had rested from all his work which God created and made These are the generations of the heavens and of the earth when they were created in the day that the LORD God made the earth and the heavens And every plant of the field before it was in the earth and every herb of the field before it grew for the LORD God had not caused it to rain upon the earth and there was not a man to till the ground But there went up a mist from the earth and watered the whole face of the ground And the LORD God formed man of the dust of the ground and breathed into his nostrils the breath of life and man became a living soul . . .

This matter was discussed in the August 1998 issue of Scientific American but the underlying principle dates back further—and was discussed in quite another context.

An article entitled ‘Sum total’ appeared in the December 1957 issue of the magic periodical Ibidem, written by the magician Alexander F. Kraus, and which brought to the world of card magic the ‘Kraus Principle’.

The magician M asks a member of the audience A to shuffle a standard pack of 52 playing cards, then secretly to pick an integer between 1 and 10. A is then asked to deal the cards, one by one and face up, to form a pile and while doing so to count them silently in the following way.

Suppose that the chosen number is 6. The sixth card dealt becomes a ‘key’ card, and its face value dictates how many more cards must be dealt to arrive at the next key card. For example, if the first key card happens to be 3, that many cards are dealt to arrive at the next key card. The procedure is repeated, generating a chain of key cards, until the pack is exhausted, and when this happens it is likely that the count dictated by the final key card will prove impossible to complete; this final key card is the secret chosen card.

Of course, the magician’s task is to identify that secret card chosen by this random process, which seems a very big ask.

In the 1970s the Kraus Principle became the ‘Kruskal Principle’, when the late Princeton physicist Martin Kruskal rediscovered the novelty that the magician has a very good chance of amazing the audience by announcing that secret card. The fact is that any two such chains will, in all likelihood, come together at some point, which means of course that they remain together from that point on—and inevitably end with the same card. The second chain is generated by the magician.

If we refer back to the ‘Bible code’ example, the passage may be thought of as a set of cards with each card numbered according to the number of letters in each word. Each starting word generates its own chain—and each chain meets at the ‘card’ named ‘earth’.

In order to make headway with an analysis we will generalize to a set of n cards which are numbered {c₁, c₂, c₃, . . . , c_n}, and this is, of course, the list of possible step sizes. Further, we will make the simplifying assumption that the two chains are equally likely to intersect at any of the n cards, with a constant probability which, for later convenience, we will write as p². If we write q = 1 − p² and I {1, 2, 3, . . . , n} as the random variable which is the card position at which they intersect, we have the standard geometric probability distribution

P(I = r) = q^{r − 1}p² for r = 1, 2, 3,. . . .

If we invoke a standard result of a geometric random variable (which is easy to prove), we have that

P(I > r) = q^r.

This means that the probability that the magician succeeds with the trick is

P = 1 − P(I > n) = 1 − qⁿ = 1 − (1 − p²)ⁿ.

Now we have to find a reasonable estimate for p² and to do this we find such for p. For each of the two chains, the average step size is which naturally generates a probability of and we will call p this probability. That is, we will estimate the probability that the two chains meet on any card using the assumption that they are ‘on average’ realizing their average step lengths and so ‘on average’ will meet in such a manner. Actually, the technical analysis belongs to the world of Markov chains and the interested reader might wish to consult the October 2001 paper of J. Lagarias, E. Rains and R. Vanderbei, The Kruskal count.¹

The Lagarias et al. argument is firmer and we produce a variant of part of it for later convenience.

Recall from chapter 6 the definition of conditional probability and the dissection of an event into its component parts to write

and

Then, for r > s, we have

With all of this in place we examine the event that the two sequences have not intersected before the nth card, that is, we will find an expression for P(I > n) (the event E above). To do this, define the random variables M₁ and A₁ to be the position of the first card chosen by the magician and the member of the audience respectively and divide all possibilities into the four categories (the events A, B, C and D) above:

This results in the decomposition

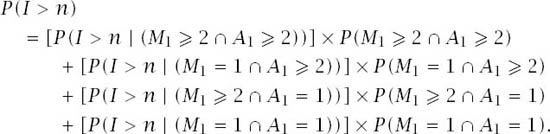
The event is precisely the event I 2 and so, using the above result,

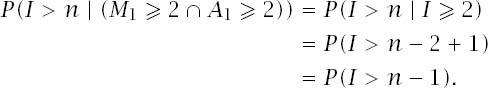
The same argument holds for each of the next two terms and the last term is 0 since

The expression therefore reduces to

and since the bracketed expression is simply P(I > 1) we are left with the recurrence relation

and chasing this down results in

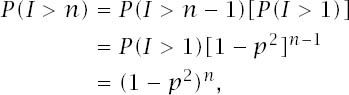
which means that the probability P of the magician performing the trick successfully is given by P = 1 − (1 − p²)ⁿ.

Now we can calculate these theoretical probabilities, making n = 52 and giving a value to p, which is, of course, entirely dependent on what values we ascribe to the cards. We will look at five reasonable alternatives.

• The spot cards are given their natural values and the jack, queen and king are given values 11, 12 and 13 respectively. The card values will be among {1, 2, 3, . . . , 13} and the average is 7. We take to get

which means that the chances of the chains meeting is about 66%.

• The spot cards are given their natural values and the court cards each count as 10. The card values will be among {1, 2, 3, . . . , 10, 10, 10, 10,} and the average is We take to get

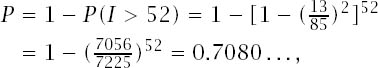
which means that the chances of the chains meeting is about 71%.

• The spot cards are given their natural values and the court cards each count as 5. The values will be among {1, 2, 3, . . . , 9, 10, 5, 5, 5} and the average is We take to get

which means that the chances of the chains meeting is now about 84%.

• The spot cards are given their natural values and the court cards each count as 1. The values will be among {1, 2, 3, . . . , 10, 1, 1, 1} and the average is We take to get

and the chances of the chains meeting becomes a very impressive 93%.

As the average value of the cards decreases, so (very reasonably) the chances of two chains meeting increases and with this in mind we can consider a particularly deceptive card assignment.

• Ignore the numbers on the cards and use the number of letters in the card names for the card numbers (ace = 3, two = 3, . . . , queen = 5, king = 4). Now the values will be among {3, 3, 5, 4, 4, 3, 5, 5, 4, 3, 4, 5, 4} and the average is We take in our estimate to get

and the chances of the chains meeting becomes an even more impressive 97%.

A little extra edge can be gained by the magician if he selects the top card of the pack, and we can use the Lagarias et al. argument to establish the details:

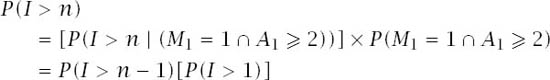
as before. Chasing this down results in

but now P(I > 1) = 1 − p since only one of the sequences has an arbitrary start and this means that and

Table 12.1. Theoretical probabilities.

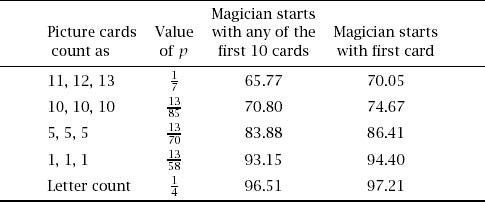
Table 12.2. Empirical probabilities.

The same calculations as above give rise to the final column of table 12.1, which gives the chances of the chains meeting under the various card enumerations, given as a percentage.

With this mixture of exactitude and heuristics it can only be right to test the model with a computer simulation and table 12.2 shows the results of such a simulation over 100 000 trials in each case.

As we have said, more sophisticated mathematical techniques can be utilized to make more firm the heuristic parts of the argument but they are rather specialized and, without considerable preparation, rather opaque. We have already mentioned the CBS series NUMB3RS in chapters 6 and 8; the 16 February 2007 episode ‘Contenders’ had Amita and Charlie use (a modified form of) the Kruskal count to help hunt down the killer of two boxers. Armed with this material, the reader might wish to revisit that DVD with renewed insight!

The Gilbreath Principle. The magician sits at a table opposite a spectator. He produces a pack of cards and casually spreads them face up to prove that they are properly mixed; he gathers them up, places them face down in a pack, cuts the pack and is just about to riffle shuffle the two parts together when he declares that the spectator should do this instead and then cut the pack and complete the cut a few times. However well or badly, the cards are riffle shuffled together, cut and returned to the magician. He conceals the pack behind his back and proceeds to bring cards four at a time to the front and place them in face-down piles on the table. When all thirteen piles of four cards have been formed each pile is turned over, and in each pile there is precisely one spade, one heart, one diamond and one club.

The spectator shuffled and cut the cards, so how could the magician tell which suit each is, even if he had arranged them in some order not obvious as they were spread? The answer is that the cards were indeed arranged and that the magician does not know the suit of each card, but he does know how to utilize Gilbreath’s Principle.

In February 1957 an American magician with the name John Russell Duck produced the first edition of his magic magazine The Cardiste in which he included the article entitled ‘The Rusduck stay-stack system’. It was the observation that, with any number of perfect riffle shuffles of the top and bottom halves of the pack (one in which cards from each of the two halves are alternately placed one upon the other) some of the original order is preserved. For example, if the cards were originally ordered as ace to king in spades, hearts, clubs and diamonds, the following would still be the case:

• each half of the pack will contain two cards of the same denomination;

• each half of the pack will contain thirteen red cards and thirteen black cards;

• each half of the pack will contain one red-suited and one black-suited card of all thirteen denominations;

• the top card will be the same denomination as the bottom card, the second from top card will be the same denomination as the second from bottom card and so on throughout the pack.

We can see that a sequence of perfect riffle shuffles does preserve a great deal of order, and magicians over the years have put this fact to bewildering use. In fact, if we distinguish between the perfect out-shuffle (in which the top card stays on top of the pack) and the perfect in-shuffle (in which the top card moves to the second position down), just 8 perfect out-shuffles or 52 perfect in-shuffles will return the pack to its original order.

What if the riffle shuffles are not perfect? Bayer and Diaconis (D. Bayer and P. Diaconis, 1992, Trailing the dovetail shuffle to its lair, Annals of Applied Probability 2:294–313) proved the surprising result that it takes about eight riffle shuffles to make every configuration of the cards (approximately) equally likely and so randomize the pack (compare this number with the approximately 2500 overhand shuffles that are needed to randomize to the same extent); if we think of the 52! = 8.07 × 10⁶⁷ possible orderings of the cards, these small numbers are themselves surprising. Riffle shuffling more than eight times does not significantly increase the randomness, and riffle shuffling less than eight times is insufficient to ensure randomness. This last point is elegantly demonstrated by the following argument that five riffle shuffles are insufficient to randomize a pack of cards:

• We take the definition of random to be that every configuration is (approximately) equally likely and show that a particular configuration is not reachable by the process.

• Number the original cards 1 to 52, starting at the top.

• At any stage of the shuffling, a rising sequence in the pack is defined to be a (possibly broken) increasing sequence of consecutive integers of maximal length, so the original pack has just one rising sequence 1, 2, 3, . . . , 51, 52.

• As the original pack is randomly cut into two parts, two rising sequences are created: the top pack and the bottom pack. Riffle shuffling the two packs together simply intersperses one rising sequence with the other; as a demonstration, consider a pack of just eight cards {1, 2, 3, 4, 5, 6, 7, 8} cut as {1, 2, 3, 4, 5} and {6, 7, 8} and riffle shuffle together to form the pack

• After the second riffle shuffle the number of rising sequences is as most 2 × 2 = 4, since each of the two rising sequences from the first shuffle has a chance of being cut into two. For example, {1, 6, 7, 2, 3, 4, 8, 5} might be cut as {1, 6, 7, 2} and {3, 4, 8, 5} and shuffled together as {1, 3, 4, 8, 6, 7, 5, 2} to result in the four rising sequences: {1, 2}, {3, 4, 5}, {8}, and {6, 7}.

• The same arguments holds for subsequent riffle shuffles and we conclude that a riffle shuffle at most doubles the number of rising sequences; after five riffle shuffles there will then be at most 32 rising sequences.

• Now consider the pack reversed, with card 52 at the top and card 1 at the bottom; this has 52 rising sequences, each of 1 card, and cannot possibly be reached in the five riffle shuffles.

It was the amateur magician Norman L. Gilbreath who deliberated on what structure remains after a single, imperfect riffle shuffle. In the June 1966 edition of another magicians’ publication, Linking Rings, there appeared descriptions by him of what have become known as ‘Gilbreath’s first and second principles’, which identify something which can be salvaged from the order of a pack of cards if the riffle shuffle is not perfect. In (nearly) his own words, his stated first principle was:

If a deck of cards, ordered in alternating colours, is cut into two parts with the bottom cards of the two parts having opposite colours, and the two parts are riffle shuffled together then each successive pair of cards is composed of one red card and one black card.

And then:

If two groups of similar cards, one in the reverse order of the other, are riffle shuffled together the two halves of the resulting group of cards are similar to the original group.

First, let us look at this second observation. By it he meant that, if we take a set of n different cards, ordered in some way, and then a second such pack but arranged in the opposite order, riffle shuffle the two of them together and separate the pack into the top and bottom equal piles, each pile will contain those n different cards in some order; there will be no omissions or repeats.

The reader might wish to experiment with this by, for example, taking the two packs of 13 cards ace to king of spades and then king to ace of hearts and riffling them together. Each half will then contain both hearts and spades, but also the full set of ace to king. Notice that the reversal of order can be accomplished subtly by having the two half packs arranged in the same order, one on top of the other, and then counting through the top half pack one card at a time, placing the cards face down on top of each other.

The analysis of this is not too hard. If we call the first pack of cards, from top to bottom, {X₁, X₂, . . . , X_n} and the second {X_n, X_{n − 1}, . . . , X₁}, they will combine to form a new pack of 2n cards which we then divide into the top half A and the bottom half B. Now suppose that X_k is the last element from the reversed pack {X_n, X_{n − 1}, . . . , X₁} to appear in A, then so must all of the set {X_n, X_{n − 1}, . . . , X_k}; this is n − k + 1 elements. It must be that {X₁, X₂, . . . , X_n} contributes n − (n − k + 1) = k − 1 elements to A, and these must be {X₁, X₂, . . . , X_{k − 1}}. This means that A must consist of the distinct elements {X₁, X₂, . . . , X_n} and, of course, so must B. It is clear that the whole matter depends on the fact that a riffle shuffle may well mix cards up but it does preserve relative order.

This analysis does not cope with the first principle, where there is a repeated pattern of red and black cards, not two blocks of identical cards in reverse order. In fact, Gilbreath’s Principle (and in reality there is only one) is precisely defined by the following statement.

Suppose that S = {X₁, X₂, X₃, . . . , X_n} is a set of n cards which are, in some agreed way, different from each other. Now take multiple copies of S and form a pack by stacking them one upon the other. Form a second pack by taking (not necessarily the same number of) multiple copies, but arranging each copy of S in reverse order. Now there are two face-down packs, not necessarily of the same size; one consisting of repeats of {X₁, X₂, X₃, . . . , X_n} and the other of {X_n, X_{n − 1}, X_{n − 2}, . . . , X₁}. Riffle shuffle the two packs together and divide the combined pack back into the sets of n cards, counting from the top. Within each set of these n cards, {X₁, X₂, X₃, . . . , X_n} will again appear in some order.

For example, if n = 2, {X₁, X₂} might be the pairing {red card, black card}, which accounts for Gilbreath’s first statement. With n = 4, {X₁, X₂, X₃, X₄} might be the set and the secret behind the magician’s trick described earlier is revealed.

In fact, in the August 1966 issue of Linking Rings, one Charles Hudson really said just that:

When a repeating series of cards is riffle shuffled into itself, with one of the packets to be shuffled being in reverse order to the other, the contents of each group in the series do not change—they are only disordered.

Again, the reader might wish to experiment with these black and red combinations or with the arrangement of the four suits; it does work, and again it is not too hard to see why. Whenever a last element X_k of a reversed pack is inserted into one of the non-reversed packs, then so is all of {X_n, X_{n − 1}, . . . , X_k} and exactly that set of cards forms the final n − k + 1 cards of the forward pack and these are forced to the top of the next forward pack of n cards—and so the cascade continues. All that remains is to explain why, in Gilbreath’s first statement about the red and black effect, the bottom pack is not reversed. In fact it is, by the statement ‘is cut into two parts with the bottom card of the two parts having opposite colours’. Of course, this means that all corresponding pairs have opposite colours and that is just a special case of a reversal! The cutting of the pack has no real effect.

Finally, if the pack is arranged in any suitable multiply structured manner, the magician can wreak even greater havoc with the spectator’s thoughts. For example, the repeated arrangement automatically allows for the magician to intersperse the production of red–black pairs with quartets of cards of each suit. Additionally, if a particular selection of denominations is chosen for the first thirteen cards and repeated three times, each consecutive set of thirteen cards will contain one card of each denomination: such an arrangement is shown below:

With the cards so arranged, top to bottom, a multiple effect would be:

• Have the spectator cut the cards and complete the cut at will.

• Ask for the cards to be dealt face down on top of each other until there is a decent pack on the table.

• Ask for the two packs to be riffle shuffled together.

• The magician produces pairs of red–black cards and quartets of different suits for the first twenty-six cards, after which the top remaining thirteen cards are dealt face up to reveal one card of each denomination, which is repeated with the final thirteen cards.

It’s all a matter of where the magician places the emphasis.

¹http://front.math.ucdavis.edu/search?a=lagarias&t=&q=&c=&n=40&s=Listings.