Chapter 17

GOODSTEIN SEQUENCES

Bigger than the biggest thing ever and then some. Much bigger than that in fact, really amazingly immense, a totally stunning size, real ‘wow, that’s big’, time . . . Gigantic multiplied by colossal multiplied by staggeringly huge is the sort of concept we’re trying to get across here.

Douglas Adams, The Restaurant at the End of the Universe

Exponential notation deals with very big numbers very efficiently. For example, 2²²² has about one million digits in it (and happens to be the biggest number which can be manufactured from four 2s using the standard arithmetic operations). In Adams’s original book of the Hitchhiker series, The Hitchhiker’s Guide to the Galaxy, appears what might be the biggest number ever used in a work of fiction: 2^{260 199}, the quoted odds against Arthur Dent and Ford Prefect being rescued by a passing spaceship, having been thrown out of an airlock. (In fact, they were rescued by a spaceship—powered by an ‘infinite improbability drive’.)

Exponential notation can be thought to be the third in the progression of the basic arithmetical operations, as addition is built on by multiplication and that in turn by exponentiation: (2 × 5 = 2 + 2 + 2 + 2 + 2) and (2⁵ = 2 × 2 × 2 × 2 × 2). It seems natural to extend the process to a fourth operation by defining repeated exponentiation: that operation is commonly given the name tetration (tetra- the Greek for four together with a part of the word iteration). A notation that has been commonly used is to put the power to the left of the base number, so, for example,

Notice that these ‘power towers’ are evaluated unambiguously from the highest power down.

Alternative names and notations exist which replace and extend the above, for example, Knuth’s up-arrow and Conway’s chained-arrow notations, but it was the English mathematical logician, philosopher and teacher Reuben Goodstein who coined the term tetration and it was he who discovered a most remarkable fact involving fantastically large numbers—and also a proof which is equally remarkable.

Goodstein Sequences

We count in base 10. This means that, for example, the number 2136 has the natural decomposition

and, generally, that for positive integers a₁, a₂, a₃, . . ., a_n < 10.

Evidently, we could use any positive integer for the base: with base 2 we have

where the nonzero a_r are necessarily 1. We can ‘complete’ this binary representation by writing the powers themselves in binary to arrive at a first stage of

and a second of

which is known as the complete base 2 representation of 2136.

Now we move to the more esoteric and define a set of ‘base bumping’ functions, starting with B₃, which acts on the complete base 2 representation of 2136 by replacing each 2 with a 3, to give

a number vastly bigger than the original.

From this we will define the Goodstein sequence G_r (n) by

which means that we subtract 1 from our number to get

and to maintain the proper base representation we have to rearrange the 3³⁺¹ term a bit, a task achieved by noting that from the theory of geometric series, for any positive integer b,

This makes

and

We continue the process with 2136 to get

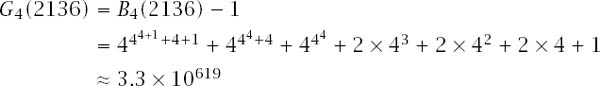
and

It seems evident that, as the iteration continues, the resulting Goodstein number will become greater and greater, but let us see what happens as we start with the smallest positive integers.

First, G₂(1) = 1 and so G₃(1) = 1 − 1 = 0 and we are finished.

Now consider the Goodstein sequence generated by 2:

and finally G₅ (2) = 1 − 1 = 0.

Again, the sequence collapses to 0. We have to work a little harder with 3: G₂ (3) = 2¹ + 1, G₃ (3) = 3¹, G₄ (3) = 4¹ − 1 = 3, G5 (3) = 2, G₆ (3) = 1 and finally G₇ (3) = 0 and the collapse occurs once more.

A Rather Big Surprise

How big must the integer be before these fantastically large numbers appear? Let us see what happens with 4. G₂ (4) = 2² = 4, G₃ (4) = 3³ − 1 = 2 × 3² + 2 × 3 + 2 = 26, G₄ (4) = 2 × 4² + 2 × 4 + 1 = 41 and continuing the procedure leads to the extended sequence:

The values of the Goodstein sequence are now growing, albeit slowly, and we have a start—which continues in a manner rather stranger than one might imagine. After precisely 3 × 2^{402 653 211} − 1 ≈ 10^{121 210 695} steps the sequence once again collapses to 0.

That is, if r = 3 × 2^{402 653 211} − 1, G_r (4) = 0, vastly big though the terms become!

David Williams has provided an argument to establish this remarkable fact, based on observations of the patterns in the Goodstein sequence of the number 4. The reader may wish to check his observations that:

1. For r 27, if m = 3 × 2^r − 1, then G_m (4) = 1 × m² + (27 − r) × m.

2. This means that, if a = 3 × 2²⁷ − 1, then G_a (4) = a².

3. Write b = a + 1 = 3 × 2²⁷ and this result becomes G_b(4) = b² − 1 = (b − 1)b + (b − 1).

4. For r b − 1, this pattern continues to G_b+r(4) = (b − 1)(b + r) + b − (r − 1).

5. This means that G_2b−1 (4) = (b − 1)(2b − 1).

6. If g = 2^sb − 1, this pattern continues to G_g (4) = (b − s)g.

7. This means that, when s = b, G_g (4) = 0.

8. Which means that G_g(4) = 0 for the first time when

Now that we have the Goodstein sequence for 4 (eventually) reaching 0 we will make the vast jump to the earlier sequence generated by 2136. Is it possible that this would eventually finish at 0 too, huge though the numbers become? Astonishingly, the answer is yes, in fact every such sequence would do the same. This 1944 result of Reuben Goodstein (On the restricted ordinal theorem, Journal of Symbolic Logic 9:33–41) is, understandably, known as Goodstein’s Theorem and simply states that every Goodstein sequence converges to 0.

‘Bumping the base’ seems inevitably to increase the size of the number hugely and subtracting 1 hardly seems to compensate for this—but the process is deceptive!

Axioms and Ordinals

The result is included here because of its surprising nature, but its importance to mathematical logic is of vastly greater moment since it provides an example of what have become known as naturally independent phenomena, which have come about as a by-product of the seminal work of Kurt Gödel. At a conference in Königsberg in September 1930, he announced his first incompleteness theorem, which destroyed the long-cherished notion of the great David Hilbert that mathematics was complete within itself; that is, that every statement expressible within it can be proved or disproved within it. Yet there remained a degree of dissatisfaction. Gödel’s construction of an undecidable statement was ‘meta-mathematical’ and there was felt to be a need for an example of such a statement which was not peculiar or contrived, one which occurs ‘naturally’ and which we would reasonably expect to be decidable one way or the other: that need was fulfilled by versions of Ramsey’s Theorem, Kruskal’s Tree Theorem and Goodstein’s Theorem, which had to wait until 1982 for J. Paris and L. Kirby to show that it is not provable within ordinary arithmetic. Since Goodstein had indeed proved his theorem back in 1944 we seem to have irreconcilable statements:

• It is true, I just proved it (Goldstein 1944).

• It is not provable one way or the other (Paris and Kirby 1982).

Of course, the reconciliation exists and it is found in a clear definition of what we mean by mathematics in this context and the somewhat exotic nature of Goodstein’s proof: the use of transfinite ordinals. The ‘ordinary arithmetic’ involved in Paris and Kirby’s argument is formally defined by the Peano axioms, which include all of the familiar rules of algebra together with the principle of induction; it is all that we need to cope with everyday mathematics. Set theory is not part of it and, most particularly, infinite sets are not accounted for; there is no place in it for Cantor’s transfinite ordinals. We saw some of the wonder of Cantor’s work in chapter 6, now we will very briefly look at some more products of his original mathematical mind.

His construction of transfinite numbers distinguishes between the use of the positive integers as a measure of size (for example, there are five elements in the set) and order (for example, that is the fifth element of the set) and here we are concerned with this latter interpretation.

Set theory (using the empty set Ø, a letter from the Norwegian alphabet apparently chosen by Andre Weil as part of the remarkable Bourbaki initiative) can be used to define the finite ordinals in the following recursive way:

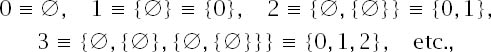
and this suggests the ordering a b if and only if a ⊆ b and with this we retrieve the familiar, natural ordering 0, 1, 2, 3, 4, . . . .

Things become a little more interesting when we consider the whole set of natural numbers {0, 1, 2, 3, . . .} and define the first transfinite ordinal ω = {0, 1, 2, 3, . . .} and the extended ordinal sequence 0, 1, 2, 3, 4, . . ., ω. This ω is distinguished in that it has no immediate predecessor and it is clear from the definition that n < ω for all integers n. The process continues as we define ω + 1 ≡ {0, 1, 2, 3, . . . , ω}, etc., to achieve the sequence

which itself continues to

and thence to

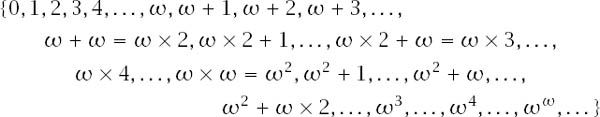
with the sequence continuing to (and beyond) the power-tower limit , which is designated ‘epsilon zero’. The familiar notation used to represent this ordinal sequence is deceptively subtle; for example, 1 + ω = ω ≠ ω + 1 and 2 × ω = ω ≠ ω × 2, but we sidestep this important matter (it depends on what is meant by ‘=’) to concentrate on a crucially important property of the set of transfinite ordinals: with the ordering above they are well ordered by , a condition defined on all ordinals a, b and c by

1. a a.

2. If a b and b c, then a c.

3. If a b and b a, then a = b.

4. Either a b or b a.

5. Every nonempty subset of the ordinals has a least element.

These seemingly innocent conditions on a set, and in particular on the set of ordinals, conceal an important consequence: in such a set there can be no infinite descending chains, that is, a b c  . . . must be of finite length.

Goodstein’s Argument

With the Goodstein process acting on a positive integer, we have a procedure which is plainly number theoretic. The assertion that the sequence inevitably converges to 0 seems to be one which can be resolved using the many powerful results of number theory, but Paris and Kirby proved otherwise: to prove the result we have to move to these transfinite ordinals, and that is what Goodstein did. The following argument puts all of the pieces in place.

First, every transfinite ordinal a < ε₀ can be written in a manner rather like the complete base representation of integers, using base ω; for example, ω^ωω + ω^ω+1 + ω. This is called Cantor’s normal form of the ordinal.

Now we define the sequence (n) parallel to the Goodstein sequence G_r (n) to be the sequence of transfinite ordinals generated by replacing the base of the Goodstein number with ω.

For example, since

Now let us begin to get a feel for this new sequence by looking at what form it takes with the number 4. The previous results were that G₂ (4) = 2², G₃ (4) = 2 × 3² + 2 × 3 + 2, G₄ (4) = 2 × 4² + 2 × 4 + 1, . . . and this means that

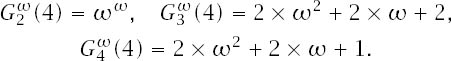
Notice that this sequence of ordinals is descending:

If the Goodstein sequence were of infinite length, it would generate this parallel sequence of descending ordinals which is infinite in length . . . and that contradicts the well-ordering result stated on page 207. Of course, this means that the Goodstein sequence of 4 must terminate in 0.

It is not very difficult to generalize the process to any Goodstein sequence

being paralleled by the decreasing ordinal sequence

to provide proof of the theorem.

The result provides a striking realization of Cantor’s own view that ‘the essence of mathematics lies in its freedom’.