Chapter Six

Adaptive PageRank

6.1 INTRODUCTION

In the previous chapter, we exploited certain properties about the matrix A (namely, its known eigenvalues) to accelerate PageRank. In this chapter, we exploit certain properties of the convergence of the Power Method on the Web matrix to accelerate PageRank. Namely, we make the following simple observation: the convergence rates of the PageRank values of individual pages during application of the Power Method are nonuniform.¹ That is, many pages converge quickly, with a few pages taking much longer. Furthermore, the pages that converge slowly are generally those pages with high PageRank.

We devise a simple algorithm that exploits this observation to speed up the computation of PageRank, called Adaptive PageRank. In this algorithm, the PageRank of pages that have converged is not recomputed at each iteration after convergence. In large-scale empirical studies, this algorithm speeds up the computation of PageRank by 17%.

6.2 DISTRIBUTION OF CONVERGENCE RATES

Table 6.1 and Figure 6.1 show convergence statistics for the pages in the STANFORD.EDU dataset. We say that the PageRank x_i of page s_i has converged when

We choose this as the measure of convergence of an individual page rather than |x_i^(k+1) − x_i^(k)| to suggest that each individual page must be accurate relative to its own PageRank. We still use the L₁ norm to detect convergence of the entire PageRank vector for the reasons that were discussed in the previous chapter.

Table 6.1 shows the number of pages and average PageRanks of those pages that converge in fewer than 15 iterations, and those pages that converge in more than 15 iterations. Notice that most pages converge in fewer than 15 iterations, and their average PageRank is one order of magnitude lower than that for those pages that converge in more than 15 iterations.

Figure 6.1(a) shows the profile of the bar graph where each bar represents a page i and the height of the bar is the convergence time t_i of that page i. The pages are sorted from left to right in order of convergence times. Notice that most pages converge in under 15 iterations, but some pages require more than 40 iterations to converge.

Table 6.1 Statistics about pages in the STANFORD.EDU dataset whose convergence times are quick (t_i ≤ 15) and pages whose convergence times are long (t_i > 15).

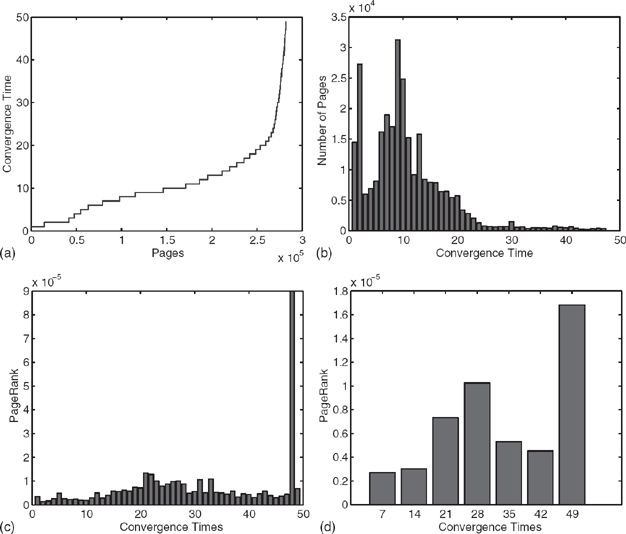
Figure 6.1 Experiments on STANFORD.EDU dataset. (a) Profile of bar graph where each bar represents a page i, and its height represents its convergence time t_i. (b) Bar graph where the x-axis represents the discrete convergence time t, and the height of t, represents the number of pages that have convergence time t. (c) Bar graph where the height of each bar represents the average PageRank of the pages that converge in a given convergence time. (d) Bar graph where the height of each bar represents the average PageRank of the pages that converge in a given interval.

Figure 6.1(b) shows a bar graph where the height of each bar represents the number of pages that converge at a given convergence time. Again, notice that most pages converge in under 15 iterations, but there are some pages that take over 40 iterations to converge.

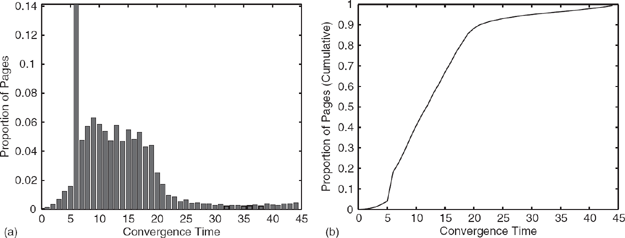
Figure 6.2 Experiments on the LARGEWEB dataset. (a) Bar graph where the x-axis represents the convergence time t in number of iterations, and the height of bar t_i represents the proportion of pages that have convergence time t. (b) Cumulative plot of convergence times. The x-axis gives the time t in number of iterations, and the y-axis gives the proportion of pages that have a convergence time ≤ t.

Figure 6.1(c) shows a bar graph where the height of each bar represents the average PageRank of the pages that converge in a given convergence time. Notice that those pages that converge in fewer than 15 iterations generally have a lower PageRank than pages that converge in more than 50 iterations. This is illustrated in Figure 6.1(d) as well, where the height of each bar represents the average PageRank of those pages that converge within a certain interval (i.e. the bar labeled “7” represents the pages that converge in anywhere from 1 to 7 iterations, and the bar labeled “42” represents the the pages that converge in anywhere from 36 to 42 iterations).

Figures 6.2 and 6.3 show some statistics for the LARGEWEB dataset. Figure 6.2(a) shows the proportion of pages whose ranks converge to a relative tolerance of .001 in each iteration. Figure 6.2(b) shows the cumulative version of the same data; that is, it shows the percentage of pages that have converged up through a particular iteration. We see that in 16 iterations, the ranks for more than two-thirds of pages have converged. Figure 6.3 shows the average PageRanks of pages that converge in various iterations. Notice that those pages that are slow to converge tend to have higher PageRank.

6.3 ADAPTIVE PAGERANK ALGORITHM

The skewed distribution of convergence times shown in the previous section suggests that the running time of the PageRank algorithm can be significantly reduced by not recomputing the PageRanks of the pages that have already converged. This is the basic idea behind the Adaptive PageRank algorithm that we motivate and present in this section.

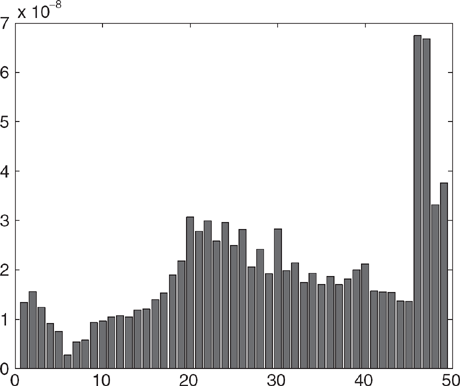
Figure 6.3 Average PageRank versus convergence time (in number of iterations) for the LARGEWEB dataset. Note that pages that are slower to converge to a relative tolerance of .001 tend to have high PageRank.

6.3.1 Algorithm Intuition

We begin by describing the intuition behind the Adaptive PageRank algorithm. We consider next a single iteration of the Power Method, and show how we can reduce the cost.

Consider that we have completed k iterations of the Power Method. Using the iterate , we now wish to generate the iterate . Let C be set of pages that have converged to a given tolerance, and N be the set of pages that have not yet converged.

We can split the matrix A defined in Section 2.2 into two submatrices. Let A_N be the m × n submatrix corresponding to the inlinks of those m pages whose PageRanks have not yet converged, and let A_C be the (n − m) × n submatrix corresponding to the inlinks of those pages that have already converged.

Let us likewise split the current iterate of the PageRank vector into the m- vector corresponding to the components of that have not yet converged, and the (m − n)-vector corresponding to the components of that have already converged.

We may order A and as follows:

and

Algorithm 10: Adaptive PageRank

We may now write the next iteration of the Power Method as

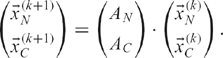
However, since the elements of have already converged, we do not need to recompute . Therefore, we may simplify each iteration of the computation to be

The basic Adaptive PageRank algorithm is given in Algorithm 10.

Identifying pages in each iteration that have converged is inexpensive. However, reordering the matrix A at each iteration is expensive. Therefore, we exploit the idea given above by periodically identifying converged pages and constructing A_N. Since A_N is smaller than A, the iteration cost for future iterations is reduced. We describe the details of the algorithm in the next section.

6.3.2 Filter-based Adaptive PageRank

Since the web matrix A is several gigabytes in size, forming the submatrix A_N needed in (6.3) will not be practical to do too often. Furthermore, if the entire matrix cannot be stored in memory, there is in general no efficient way to simply “ignore” the unnecessary entries (e.g., edges pointing to converged pages) in A if they are scattered throughout A. This is because the time spent reading the portions of the matrix to and from disk is generally much longer than the floating point operations saved. We describe in this section how to construct A_N efficiently and periodically.

Consider the following reformulation of the algorithm that was described in the previous section. Consider the matrix A as described in (6.2). Note that the submatrix A_C is never actually used in computing . Let us define the matrix A′ as

where we have replaced A_C with an all-zero matrix of the same dimensions as A_C. Similarly, let us define as

Now note that we can express an iteration of Adaptive PageRank as

Since A′ has the same dimensions as A, it seems we have not reduced the iteration cost; however, note that the cost of the matrix-vector multiplication is essentially given by the number of nonzero entries in the matrix, not the matrix dimensions.²

The above reformulation gives rise to the filter-based Adaptive PageRank scheme: if we can periodically increase the sparsity of the matrix A, we can lower the average iteration cost. Consider the set of indices C of pages that have been identified as having converged. We define the matrix A″ as

In other words, when constructing A″, we replace the row i in A with zeros if i ∈ C. Similarly, define as

Note that A″ is much sparser than A, so that the cost of the multiplication is much less than the cost of the multiplication . In fact, the cost is the same as if we had an ordered matrix and performed the multiplication . Now note that

represents an iteration of the Adaptive PageRank algorithm. No special ordering of page identifiers was assumed.

The key parameter in the above algorithm is how often to identify converged pages and construct the “compacted” matrix A″; since the cost of constructing A″ from A is on the order of the cost of the multiply , we do not want to apply it too often. However, looking at the convergence statistics given in Section 6.2, it is clear that even periodically filtering out the “converged edges” from A will be effective in reducing the cost of future iterations. The iteration cost will be lowered for three reasons:

1. reduced i/o for reading in the link structure

2. fewer memory accesses when executing Algorithm 1

3. fewer flops when executing Algorithm 1.

Algorithm 11: Filter-based Adaptive PageRank

6.4 EXPERIMENTAL RESULTS

In our experiments, we found that better speedups were attained when we ran Algorithm 11 in phases, where in each phase we begin with the original unfiltered version of the link structure, iterate a certain number of times (in our case 8), filter the link structure, and iterate some additional number of times (again 8). In successive phases, we reduce the tolerance threshold. In each phase, filtering using this threshold is applied once, after the 8th iteration. This strategy tries to keep all pages at roughly the same level of error while computing successive iterates to achieve some specified final tolerance.

A comparison of the total cost of the standard PageRank algorithm and the Adaptive PageRank algorithm follows. Figure 6.4(a) depicts the total number of floating point operations needed to compute the PageRank vector to an L₁ residual threshold of 10⁻³ and 10⁻⁴ using the Power Method and the Adaptive Power Method. The Adaptive algorithm operated in phases as described above using 10⁻², 10⁻³, and 10⁻⁴ as the successive tolerances. Note that the adaptive method decreases the number of FLOPS needed by 22.6% and 23.6% in reaching final L₁ residuals of 10⁻³ and 10⁻⁴, respectively. Figure 6.4(b) depicts the total wallclock time needed for the same scenarios. The adaptive method reduces the wallclock time needed to compute the PageRank vectors by 14% and 15.2% in reaching final L₁ residuals of 10⁻³ and 10⁻⁴, respectively. Note that the adaptive method took 2 and 3 more iterations for reaching 10⁻³ and 10⁻⁴, respectively, than the standard Power Method, as shown in Figure 6.4(c); however, as the average iteration cost was lower, speedup still occurred.

6.5 EXTENSIONS

In this section, we present several extensions to the basic Adaptive PageRank algorithm that should further speed up the computation of PageRank.

6.5.1 Further Reducing Redundant Computation

The core of the Adaptive PageRank algorithm is in replacing the matrix multiplication with (6.3) and (6.4), reducing redundant computation by not recomputing the PageRanks of the pages in C (those pages that have converged).

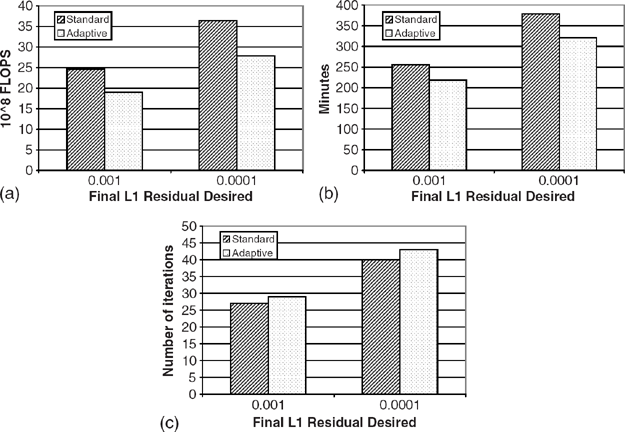
Figure 6.4 Experiments on LARGEWEB dataset depicting total cost for computing the PageRank vector to an L₁ residual threshold of 10⁻³ and 10⁻⁴. (a) FLOPS; (b) wallclock time; (c) number of iterations.

In this section, we show how to further reduce redundant computation by not recomputing the components of the PageRanks of those pages in N due to links from those pages in C.

More specifically, we can write the matrix A in (6.2) as

where A_NN are the links from pages that have not converged to pages that have not converged, A_CN are links from pages that have converged to pages that have not converged, and so on.

We may now rewrite (6.3) as follows:

Since does not change at each iteration, the component does not change at each iteration. Therefore, we only need to recompute compute each time the matrix A is reordered.

An algorithm based on this idea may proceed as in Algorithm 12. We expect that this algorithm should speed up the computation of PageRank even further than the speedups due to the standard Adaptive PageRank algorithm, but we have not investigated this empirically.

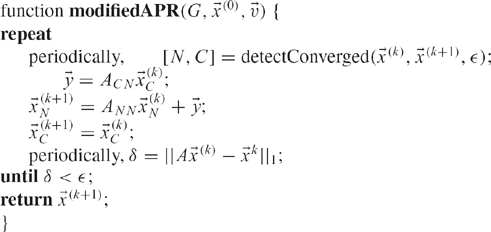
Algorithm 12: Modified Adaptive PageRank

6.5.2 Using the Matrix Ordering from the Previous Computation

PageRank is computed several times per month, and it is likely that the convergence times for a given page will not change dramatically from one computation to the next. This suggests that the matrix A should be initially ordered by convergence time in the previous PageRank computation. That is, the page corresponding to i = 1 should be the page that took the longest to converge during the last PageRank computation, and the page corresponding to i = n should be the page that converged most quickly during the last PageRank computation. This should minimize the cost incurred by matrix reorders.

6.6 DISCUSSION

In this chapter, we presented two contributions.

First, we showed that most pages on the Web converge to their true PageRank quickly, while relatively few pages take much longer. We further showed that those slow-converging pages generally have high PageRank, and the pages that converge quickly generally have low PageRank.

Second, we developed an algorithm, called Adaptive PageRank, that exploits this observation to speed up the computation of PageRank by 17% by avoiding redundant computation. Finally, we discussed several extensions of Adaptive PageRank that should further speed up PageRank computations.

The next chapter presents an algorithm called BlockRank, which exploits yet another property of the Web, its intrahost versus interhost linkage patterns.