Chapter Four
The Condition Number of the PageRank Problem
In the previous chapter, we showed convergence properties of the PageRank problem. In this chapter, we focus on stability. In particular, the following shows that the PageRank problem is well-conditioned for values of c that are not very close to 1.
4.1 THEOREM 6
Theorem 6. Let P be an n × n row-stochastic matrix whose diagonal elements Pii = 0. Let c be a real number such that 0 ≤ c ≤ 1. Let E be the n × n rank-one row-stochastic matrix E =
, where 
is the n-vector whose elements are all ei = 1, and 
is an n-vector that represents a probability distribution.1
Define the matrix A = [cP + (1 – c)E]T. The problem A
= has condition number κ = (1 + c)/(1 – c).
4.2 PROOF OF THEOREM 6
We prove this case via a series of lemmas.
LEMMA 1. ET= .
Proof. By definition, E =
. Therefore, ET = 
. From (2.4), T = 1. Therefore, ET = .
LEMMA 2. The eigenvalue problem A = : can be rewritten as the nonsingular system of equations (I – cPT): = (1 – c).
Proof. From A = , we can rearrange terms to get
(I – A) = 0.
By the definition of A (equation 2.2)
[I – (cP + (1 – c)E)T] = 0.
From Lemma 1, ET: = . Therefore, (I – cPT): – (1 – c) = 0. Rearranging terms, we get (I – cPT): = (1 – c).
LEMMA 3. = (I – cPT)–1.
Proof. Let M = I – cPT. Then MT = I – cP. Since P has zeros on the diagonals and is row-stochastic, and since c < 1, I – cP is strictly diagonally dominant and therefore invertible. Since MT is invertible, M is also invertible. Therefore, we may write = (I – cPT)–1.
LEMMA 4. ||I – cPT||1 = 1 + c.
Proof. Since the diagonal elements of cPT are all zero,
||I – cPT ||1 = ||I ||1 + c||PT ||1 = 1 + c||PT ||1.
Since PT is a column-stochastic matrix, || PT || 1 = 1. Thus, || I – cPT || 1 = 1 + c.
LEMMA 5. ||(I – cPT)–1||1 = 1/(1 – c).
Proof. Recall from (2.2) that A = [cP + (1 – c)E]T, where E = and v is some n-vector whose elements are non-negative and sum to 1. Let (
) be the n-vector that satisfies the following equations:
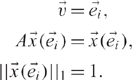
From Lemma 2, = (1—c)(I—cPT)–1. Therefore, () = (1—c)(I—cPT)–1. Taking the norm of both sides gives ||()||1 = (1 – c)|(I – cPT)–1 ||1. Since |()||1 = 1, we have
||(I – cPT)–1||1 = 1/(1 – c). (4.1)
Notice that (I – cPT)–1 gives the ith column of (I – cPT)–1. Thus, from (4.1), the L1 norm of the matrix (I – cPT)–1 is ||(I – cPT)–1|| = 1/(1 – c)
LEMMA 6. The 1-norm condition number of = (I – cPT)–1 is κ = (1 + c)/ (1 – c).
Proof. By definition, the 1-norm condition number κ of the problem 
= M–1
is given by κ = ||M||1||M–1||1. From Lemmas 4 and 5, this is κ = (1 + c)/(1 – c).
4.3 IMPLICATIONS
The strongest implication of this result has to do with the stability of PageRank. A proof of stability of PageRank is given in [55], but we show a tighter stability bound here. Imagine that the Google matrix A is perturbed slightly, either by modifying the link structure of the Web (by adding or taking away links), or by changing the value of c. Let us call this perturbed matrix à = A + 
B, where B is the “error matrix” describing the change to the Web matrix A. Let be the PageRank vector corresponding to the Web matrix A, and let 
be the vector corresponding to the Web matrix A. It is known that, for a linear system of equations,
|-|1 ≤ κ | B |.
From Theorem 6, we can rewrite this as
What this means is that, for values of c near to 1, PageRank is not stable, and a small change in the link structure may cause a large change in PageRank. However, for smaller values of c such as those likely to be used by Google (.8 < c < .9), PageRank is stable, and a small change in the link structure will cause only a small change in PageRank.
Another implication of this is the accuracy to which PageRank may be computed. Again, for values of c likely to be used by Google, PageRank is a well-conditioned problem meaning that it may be computed accurately by a stable algorithm. However, for values of c close to 1, PageRank is an ill-conditioned problem, and it cannot be computed to great accuracy by any algorithm.
1 i.e., a vector whose elements are nonnegative and whose L1 norm is 1.