Chapter Two
![]()
PageRank
2.1 PAGERANK BASICS
The PageRank algorithm for determining the reputation of Web pages has become a central technique in Web search [56]. The core of the PageRank algorithm involves computing the principal eigenvector of the Markov matrix representing the hyperlink structure of the Web. As the Web graph is very large, containing several billion nodes, the PageRank vector is generally computed offline, during the preprocessing of the Web crawl, before any queries have been issued. As discussed in Chapter 1, personalization requires significant advances to the standard PageRank algorithm.
This chapter reviews the standard PageRank algorithm [56] and some of the mathematical tools that will be used in analyzing and improving the standard iterative algorithm for computing PageRank throughout the rest of this book.
Underlying PageRank is the following basic assumption. A link from a Web page u to another page v can be viewed as evidence that v is an “important” page.1 In particular, the amount of importance conferred on v by u is proportional to the importance of u and inversely proportional to the number of pages u points to. Since the importance of u is itself not known, determining the importance for every page i in the Web requires an iterative fixed-point computation.
To allow for a more rigorous analysis of the necessary computation, we next describe an equivalent formulation in terms of a random walk on the directed Web graph G. (The graph G is the directed graph where each node represents a page on the Web, and an edge between nodes u and v represents a link from page u to page v.) Let u → v denote the existence of an edge from u to v in G. Let deg(u) be the outdegree of page u in G. Consider a random surfer visiting page u at time k. In the next time step, the surfer chooses a node vi from among u’s out-neighbors {v|u → v} uniformly at random. In other words, at time k + 1, the surfer lands at node vi ![]() {v|u → v} with probability 1/deg(u).
{v|u → v} with probability 1/deg(u).
The PageRank of a page i is defined as the probability that at some particular time step k > K, the surfer is at page i. In the limit as K → ∞, this probability distribution is called the stationary probability distribution.
With minor modifications to the random walk, this probability distribution is unique, illustrated as follows. Consider the Markov chain induced by the random walk on G, where the states are given by the nodes in G and the stochastic transition matrix describing the transition from i to j is given by Q with Qij = 1/deg(i).
For Q to be a valid transition probability matrix, every node must have at least 1 outgoing transition; that is, Q should have no rows consisting of all zeros. This holds if G does not have any pages with outdegree 0, which is not the case for the Web graph. Q can be converted into a valid transition matrix by adding a complete set of outgoing transitions to pages with outdegree 0. In other words, we can define the new matrix P where all states have at least one outgoing transition in the following way. Let n be the number of nodes (pages) in the Web graph. Let ![]() be the n-dimensional column vector representing a uniform probability distribution over all nodes:
be the n-dimensional column vector representing a uniform probability distribution over all nodes:
![]()
Let ![]() be the n-dimensional column vector identifying the nodes with outdegree 0:
be the n-dimensional column vector identifying the nodes with outdegree 0:
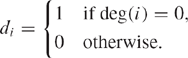
Then we construct P′ as follows:
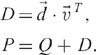
In terms of the random walk, the effect of D is to modify the transition probabilities so that a surfer visiting a dangling page (a page with no outlinks) randomly jumps to another page in the next time step, using the distribution given by ![]()
By the ergodic theorem for Markov chains [31], the Markov chain defined by P has a unique stationary probability distribution if P is aperiodic and irreducible. In general, neither of these properties holds for the Markov chain induced by the Web graph.
In the context of computing PageRank, the standard way of ensuring these properties is to add a new set of complete outgoing transitions, with small transition probabilities, to all nodes, creating a strongly connected (and thus irreducible) transition graph. Furthermore, adding this set of outgoing transitions will ensure that the transition graph has at least one self-loop, thus guaranteeing aperiodicity. For a more in-depth discussion of these conditions, see [31].
In matrix notation, we construct the aperiodic, irreducible Markov matrix P′ as follows:
E = [1]n×1 × ![]() T,
T,
P′ = cP + (1 − c)E.
In terms of the random walk, the effect of E is as follows. At each time step, with probability (1 − c), a surfer visiting any node will jump to a random Web page (rather than following an outlink). The destination of the random jump is chosen according to the probability distribution given in ![]() . Artificial jumps taken because of E are referred to as teleportation.
. Artificial jumps taken because of E are referred to as teleportation.
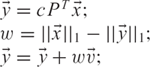
Algorithm 1: Computing ![]() = A
= A![]()
By redefining the vector ![]() given in (2.1) to be nonuniform, so that D and E add artificial transitions with nonuniform probabilities, the resultant PageRank vector can be biased to prefer certain kinds of pages. For this reason, we refer to
given in (2.1) to be nonuniform, so that D and E add artificial transitions with nonuniform probabilities, the resultant PageRank vector can be biased to prefer certain kinds of pages. For this reason, we refer to ![]() as the personalization vector.
as the personalization vector.
For simplicity and consistency with prior work, the remainder of the discussion will be in terms of the transpose matrix, A = (P′)T; that is, the transition probability distribution for a surfer at node i is given by row i of P′ and column i of A.
Note that the edges artificially introduced by D and E never need to be explicitly materialized, so this construction has no impact on efficiency or the sparsity of the matrices used in the computations. In particular, the matrix-vector multiplication ![]() = A
= A![]() can be implemented efficiently using Algorithm 1.
can be implemented efficiently using Algorithm 1.
Assuming that the probability distribution over the surfer’s location at time 0 is given by ![]() (0), the probability distribution for the surfer’s location at time k is given by
(0), the probability distribution for the surfer’s location at time k is given by ![]() (k) = Ak
(k) = Ak![]() (0). The unique stationary distribution of the Markov chain is defined as limk→∞ x(k), which is equivalent to limk→∞ Akx(0) and is independent of the initial distribution
(0). The unique stationary distribution of the Markov chain is defined as limk→∞ x(k), which is equivalent to limk→∞ Akx(0) and is independent of the initial distribution ![]() (0). This is simply the principal eigenvector of the matrix A = (P′′)T [31], which is exactly the PageRank vector we would like to compute.
(0). This is simply the principal eigenvector of the matrix A = (P′′)T [31], which is exactly the PageRank vector we would like to compute.
The standard PageRank algorithm computes the principal eigenvector by starting with the uniform distribution ![]() (0) =
(0) = ![]() and computing successive iterates
and computing successive iterates ![]() (k) = A
(k) = A![]() (k−1) until convergence. This is known as the Power Method, and is discussed in further detail in Section 2.3. The next section summarizes some of the notation described in the section, and introduces some new notation that will be used later on in this book.
(k−1) until convergence. This is known as the Power Method, and is discussed in further detail in Section 2.3. The next section summarizes some of the notation described in the section, and introduces some new notation that will be used later on in this book.
2.2 NOTATION AND MATHEMATICAL PRELIMINARIES
We will use the following notation and simple mathematical preliminaries throughout this book.
P is an n × n row-stochastic matrix. E is the n × n rank-one row-stochastic matrix E = ![]()
![]() T where
T where ![]() is the n-vector whose elements are all ei = 1. A is the n × n column-stochastic matrix
is the n-vector whose elements are all ei = 1. A is the n × n column-stochastic matrix
| A = [cP + (1 - c)E]T. | (2.2) |
We denote the ith eigenvalue of A as λi, and the corresponding eigenvector as ![]() i.
i.
| A |
(2.3) |
By convention, we choose eigenvectors ![]() i such that ||
i such that ||![]() i||1 = 1.2 Since A is a non-negative matrix, the dominant eigenvector
i||1 = 1.2 Since A is a non-negative matrix, the dominant eigenvector ![]() is also non-negative. Therefore,
is also non-negative. Therefore,
![]()
Since A is column-stochastic, λ1 = 1, 1 ≥ |λ2| ≥ … ≥ |λn|≥ 0.
Since the eigenvalues of AT are the same as those of A, we know that the first eigenvalue of AT is also 1. Furthermore, since AT is row-stochastic, it can be shown by inspection that the corresponding eigenvector of AT is ![]() /n.
/n.
We denote the ith eigenvalue of PT as γi, and its corresponding eigenvector as ![]() i: PT
i: PT ![]() i = γi
i = γi![]() i. Since PT is column-stochastic, γ1 = 1, 1 ≥ |γ2| ≥ … ≥ |γn| ≥ 0.
i. Since PT is column-stochastic, γ1 = 1, 1 ≥ |γ2| ≥ … ≥ |γn| ≥ 0.
We denote the ith eigenvalue of ET as μi, and its corresponding eigenvector as ![]() i: ET
i: ET![]() i. = μi
i. = μi![]() i. Since ET is rank-one and column-stochastic, μ1 = 1, μ2 = … = μn = 0.
i. Since ET is rank-one and column-stochastic, μ1 = 1, μ2 = … = μn = 0.
An n × n row-stochastic matrix M can be viewed as the transition matrix for a Markov chain with n states.
For any row-stochastic matrix M, M![]() =
= ![]() .
.
A set of states S is a closed subset of the Markov chain corresponding to M if and only if i ![]() S and j
S and j ![]() S implies that Mij = 0.
S implies that Mij = 0.
A set of states S is an irreducible closed subset of the Markov chain corresponding to M if and only if S is a closed subset, and no proper subset of S is a closed subset.
Intuitively speaking, each irreducible closed subset of a Markov chain corresponds to a leaf node in the strongly connected component (SCC) graph of the directed graph induced by the nonzero transitions in the chain.
Note that E, P, and AT are row-stochastic, and can thus be viewed as transition matrices of Markov chains.
2.3 POWER METHOD
2.3.1 Formulation
The Power Method (Algorithm 2) is the oldest method for computing the principal eigenvector of a matrix, and is at the heart of both the motivation and implementation of the original PageRank algorithm (in conjunction with Algorithm 1).
The intuition behind the convergence of the Power Method is as follows. For simplicity, assume that the start vector ![]() (0) lies in the subspace spanned by the eigenvectors of A.3 Then
(0) lies in the subspace spanned by the eigenvectors of A.3 Then ![]() (0) can be written as a linear combination of the eigenvectors of A:
(0) can be written as a linear combination of the eigenvectors of A:
![]()
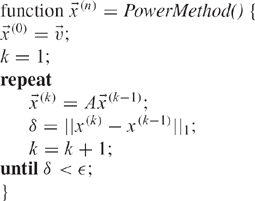
Algorithm 2: Power Method
If we choose ![]() (0) such that ||
(0) such that ||![]() (0)||1 = 1 and all the elements of
(0)||1 = 1 and all the elements of ![]() (0) are nonnegative, we can show that α1 = 1 as follows:
(0) are nonnegative, we can show that α1 = 1 as follows:
![]()
Since ||![]() (0)||1 = 1 and all the elements of
(0)||1 = 1 and all the elements of ![]() (0) are non-negative, (
(0) are non-negative, (![]() (0))T
(0))T![]() = 1. Thus we have
= 1. Thus we have
![]()
Recall from Section 2.2 that the dominant eigenvector of AT is ![]() . The right eigenvectors of any matrix are orthogonal to its left eigenvectors. Therefore
. The right eigenvectors of any matrix are orthogonal to its left eigenvectors. Therefore
![]()
for all k ≠ 1. Thus
![]()
Finally, since ![]() 1 represents the stationary distribution of a Markov chain, we know that all its elements are non-negative and its L1 norm is 1. Therefore,
1 represents the stationary distribution of a Markov chain, we know that all its elements are non-negative and its L1 norm is 1. Therefore, ![]() T1
T1![]() = 1, and
= 1, and
| 1 = α1. | (2.9) |
Therefore, we can rewrite (2.5) to be
![]()
Since we know that the first eigenvalue of a Markov matrix is λ1 = 1, we have
![]()
and
![]()
Since λn ≤ … ≤ λ2 < 1, A(n)![]() (0) approaches
(0) approaches ![]() 1 as n grows large. Therefore, the Power Method converges to the principal eigenvector of the Markov matrix A.
1 as n grows large. Therefore, the Power Method converges to the principal eigenvector of the Markov matrix A.
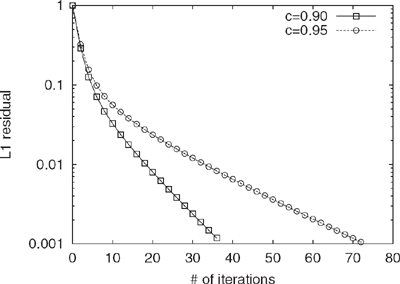
Figure 2.1 Comparison of convergence rate for the standard Power Method on the LARGEWEB dataset for c = 0.90 and c = 0.95.
2.3.2 Operation Count
A single iteration of the Power Method consists of the single matrix-vector multiply A![]() (k). Generally, this is an O(n2) operation. However, if the matrix-vector multiply is performed as in Algorithm 1, the matrix A is so sparse that the matrix-vector multiply is essentially O(n). In particular, the average outdegree of pages on the Web has been found to be around 7 [44]. In our datasets, we observed an average of around 8 outlinks per page.
(k). Generally, this is an O(n2) operation. However, if the matrix-vector multiply is performed as in Algorithm 1, the matrix A is so sparse that the matrix-vector multiply is essentially O(n). In particular, the average outdegree of pages on the Web has been found to be around 7 [44]. In our datasets, we observed an average of around 8 outlinks per page.
It should be noted that if λ2 is close to 1, then the Power Method is slow to converge, because n must be large before λn2 is close to 0, and vice versa.
2.3.3 Convergence
We will show in Chapter 3 that the eigengap 1—|λ2| for the Web Markov matrix A is given exactly by the teleport probability 1–c. Thus, when the teleport probability is large, and the personalization vector ![]() is uniform over all pages, the Power Method works reasonably well. However, for a large teleport probability (and a uniform
is uniform over all pages, the Power Method works reasonably well. However, for a large teleport probability (and a uniform ![]() ), the effect of link spam is increased, and pages can achieve unfairly high rankings.4 In the extreme case, for a teleport probability of 1 – c = 1, the assignment of rank to pages becomes uniform. Chakrabarti et al. [16] suggest that c should be tuned based on the connectivity of topics on the Web. Such tuning has generally not been possible, as the convergence of PageRank slows down dramatically for small values of 1 – c (values of c close to 1).
), the effect of link spam is increased, and pages can achieve unfairly high rankings.4 In the extreme case, for a teleport probability of 1 – c = 1, the assignment of rank to pages becomes uniform. Chakrabarti et al. [16] suggest that c should be tuned based on the connectivity of topics on the Web. Such tuning has generally not been possible, as the convergence of PageRank slows down dramatically for small values of 1 – c (values of c close to 1).
In Figure 2.1, we show the convergence on the LARGEWEB dataset5 of the Power Method for c ![]() {0.90, 0.95} using a uniform
{0.90, 0.95} using a uniform ![]() . Note that increasing c slows down convergence. Since each iteration of the Power Method takes 10 minutes, computing 100 iterations requires over 16 hours. As the full Web is estimated to contain over 2 billion static pages, using the Power Method on Web graphs close to the size of the Web would require several days of computation. We use the experimental setup described in the next section to empirically evaluate the convergence rate of the algorithms described in this book.
. Note that increasing c slows down convergence. Since each iteration of the Power Method takes 10 minutes, computing 100 iterations requires over 16 hours. As the full Web is estimated to contain over 2 billion static pages, using the Power Method on Web graphs close to the size of the Web would require several days of computation. We use the experimental setup described in the next section to empirically evaluate the convergence rate of the algorithms described in this book.
2.4 EXPERIMENTAL SETUP
The setup for the experiments in this book is as follows.
We used three datasets of different sizes for our experiments. The STANFORD. EDU link graph was generated from a crawl of the stanford.edu domain created in September 2002 by the Stanford WebBase project [36]. This link graph contains roughly 280,000 nodes, with 3 million links, and requires 12MB of storage. The STANFORD/BERKELEY link graph was generated from a crawl of the stanford.edu and berkeley.edu domains created in December 2002 by the Stanford WebBase project. This link graph (after dangling node removal, discussed below) contains roughly 683,500 nodes, with 7.6 million links, and requires 25MB of storage. We used STANFORD.EDU and STANFORD/BERKELEY while developing the algorithms, to get a sense for their performance. For real-world performance measurements, we used the LARGEWEB link graph, generated from a crawl of the Web that had been created by the Stanford WebBase project in January 2001 [36]. The full version of this graph, termed FULL-LARGEWEB, contains roughly 290M nodes, with just over a billion edges, and requires 6GB of storage. Many of these nodes are dangling nodes (pages with no outlinks), either because the pages genuinely have no outlinks, or because they are pages that have been discovered but not crawled. In computing PageRank, these nodes are excluded from the Web graph until the final few iterations, so we also consider the version of LARGEWEB with dangling nodes removed, termed DNR-LARGEWEB, which contains roughly 70M nodes, with over 600M edges, and requires 3.6GB of storage. The link graphs are stored using an adjacency list representation, with pages represented as 4-byte integer identifiers. On an AMD Athlon 1533MHz machine with a 6-way RAID-5 disk volume and 3.5GB of main memory, each iteration of PageRank on the 70M page DNR-LARGEWEB dataset takes roughly 7 minutes. Given that computing PageRank generally requires up to 100 iterations, the need for fast computational methods for larger graphs with billions of nodes is clear.
We measured the relative rates of convergence of the algorithms that follow using the L1 norm of the residual vector; that is,
![]()
We describe why the L1 residual is an appropriate measure in Section 5.5.
2.5 RELATED WORK
2.5.1 Fast Eigenvector Computation
The field of numerical linear algebra is a mature field, and many algorithms have been developed for fast eigenvector computations. However, many of these algorithms are unsuitable for this problem, because they require matrix inversions or matrix decompositions that are prohibitively expensive (in terms of both size and space) for a matrix of the size and sparsity of the Web-link matrix. For example, inverse iteration will find the principal eigenvector of A in one iteration, since we know the first eigenvalue. However, inverse iteration requires the inversion of A, which is an O(n3) operation. The QR algorithm with shifts is also a standard fast method for solving nonsymmetric eigenvalue problems. However, the QR algorithm requires a QR factorization of A at each iteration, which is also an O(n3) operation.
However, there is a class of methods from numerical linear algebra that are useful for this problem. We may rewrite the eigenproblem A![]() =
= ![]() as the linear system of equations (I – A)
as the linear system of equations (I – A)![]() = 0, and use the classical iterative methods for linear systems: Jacobi, Gauss-Seidel, and Successive Overrelaxation (SOR). For the matrix A in the PageRank problem, the Jacobi method is equivalent to the Power Method, but Gauss-Seidel has been shown empirically to be faster for the PageRank problem [7]. Note, however, that to use Gauss-Seidel, we would have to sort the adjacency-list representation of the Web graph, so that back-links for pages, rather than forward-links, are stored consecutively. The Arnoldi algorithm is also often used for nonsymmetric eigenvalue problems. Work by Golub and Greif [29] explores the use of variants of the Arnoldi algorithm for the PageRank problem. For a comprehensive review of these methods, see [30]. The myriad of multigrid methods are also applicable to this problem. For a review of multigrid methods, see [48].
= 0, and use the classical iterative methods for linear systems: Jacobi, Gauss-Seidel, and Successive Overrelaxation (SOR). For the matrix A in the PageRank problem, the Jacobi method is equivalent to the Power Method, but Gauss-Seidel has been shown empirically to be faster for the PageRank problem [7]. Note, however, that to use Gauss-Seidel, we would have to sort the adjacency-list representation of the Web graph, so that back-links for pages, rather than forward-links, are stored consecutively. The Arnoldi algorithm is also often used for nonsymmetric eigenvalue problems. Work by Golub and Greif [29] explores the use of variants of the Arnoldi algorithm for the PageRank problem. For a comprehensive review of these methods, see [30]. The myriad of multigrid methods are also applicable to this problem. For a review of multigrid methods, see [48].
2.5.2 PageRank
Much work has been done on improving PageRank and other link-based algorithms (such as HITS [45]), and extending them to new search and text mining tasks [12, 15, 17, 34, 59, 62]. More applicable to our work are several papers which discuss the computation of PageRank itself [7, 33, 39]. Haveliwala [33] explores memory-efficient computation, and suggests using induced orderings, rather than residuals, to measure convergence. Arasu et al. [7] use the Gauss-Seidel method to speed up convergence, and look at possible speed-ups by exploiting structural properties of the Web graph. Jeh and Widom [39] explore the use of dynamic programming to compute a large number of personalized PageRank vectors simultaneously. [6] and [49] provide a broader review of PageRank, its mathematical properties, and computational methods to compute PageRank. The work presented in this book is the first to develop novel techniques in numerical linear algebra designed specifically for the PageRank problem.
1 This assumption is reasonably credible, although there are of course certain exceptions. Sponsored links, links from guestbooks, and links suggesting negative endorsements all exist on the Web. Furthermore, other algorithms such as HITS [45] have a different interpretation of link semantics. HITS is discussed later in this chapter.
2 In much of the literature, the eigenvectors are chosen so that ||![]() i||2 = 1. However, in the Markov chain literature, often the eigenvectors are chosen so that ||.
i||2 = 1. However, in the Markov chain literature, often the eigenvectors are chosen so that ||.![]() i||1 = 1. This is so that the dominant eigenvector has the probabilistic interpretation as the stationary distribution of the Markov chain.
i||1 = 1. This is so that the dominant eigenvector has the probabilistic interpretation as the stationary distribution of the Markov chain.
3 This assumption does not affect convergence guarantees.
4 A high teleport probability means that every page is given a fixed “bonus” rank. Link spammers can make use of this bonus to generate local structures to inflate the importance of certain pages.
5 The LargeWeb dataset is described in Section 2.4.
