CHAPTER 12
Symbolic Programming with Structured Data
Symbols are everywhere. Numbers are symbols that stand for quantities, and you can add, multiply, or take square roots of numbers that are so small or large that it’s hard to imagine the quantity they represent. You can solve equations, multiply polynomials, approximate functions using series, and differentiate or integrate numerically or symbolically—these are just a few everyday examples of using symbols in mathematics.
It would be a mistake to think symbols are useful only in mathematics and related fields. General problem-solving can’t do without symbols; they provide the ability to abstract away details to make the larger picture clearer and help you understand relationships that may not appear obvious otherwise. Symbols always stand for something and have an attached meaning; they’re created to bind this additional content to an existing object. This gives you an extraordinary tool to solve problems, describe behavior, make strategic decisions, create new words, and write poetry—the list could go on forever.
F# is well suited for symbolic computations. This chapter covers in depth two symbolic manipulation problems. First, it presents an implementation of a symbolic differentiation application, including expression rendering using techniques based on Windows Forms programming. The second example shows how you can use symbolic programming to model hardware circuits and presents the core of a symbolic hardware-verification engine based on binary decision diagrams. We could have chosen other examples of symbolic programming, but we found these two particularly enjoyable to code in F#.
Chapter 9 already covered many of the foundational techniques for symbolic programming. One technique that is particularly important in this chapter is the use of discriminated unions to capture the shape of the abstract syntax trees for symbolic languages. Using functions as first-class values and applying recursive problem decomposition also leads to a natural and clean approach to computations on symbolic entities. These and other features of F# combine to make symbolic programming concise and painless, allowing you to focus on the really interesting parts of your application domain.
Verifying Circuits with Propositional Logic
The next example turns to a traditional application area for functional programming: describing digital hardware circuits and symbolically verifying their properties. We assume a passing familiarity with hardware design, but if you haven’t looked inside a microprocessor chip for some time, a brief recap is included in the “About Hardware Design” sidebar.
In this example, you model circuits by propositional logic, a simple and familiar symbolic language made up of constructs such as AND, OR, NOT, and TRUE/FALSE values. You then implement an analysis that converts propositional logic formulae into a canonical form called binary decision diagrams (BDDs). Converting to a canonical form allows you to check conditions and properties associated with the digital circuits.
About Hardware Design
Note The examples in this section are inspired by the tutorials for the HOL88 system, a symbolic theorem prover implemented using an F#-like language that has been used for many purposes, including hardware verification. The carry/select adder and the BDD implementation follow those given by John Harrison in his HOL Light version of the same system. You can find out more about these and other systems, as well as delve into theorem proving, in Handbook of Practical Logic and Automated Reasoning by John Harrison (Cambridge University Press, 2009).
Representing Propositional Logic
You begin by using language-oriented programming techniques to implement a little logic of Boolean expressions, of the kind that might be used to describe part of a hardware circuit or a constraint. Let’s assume these have forms like the following:
P1 AND P2
P1 OR P2
P1 IMPLIES P2
NOT(P1)
v -- variable, ranging over true/false
TRUE
FALSE
Exists v. P[v] -- v ranges over true/false, P may use v
Forall v. P[v] -- v ranges over true/false, P may use v
This is known as quantified Boolean formulae (QBF) and is an expressive way of modeling many interesting problems and artifacts that work over finite data domains. Listing 12-1 shows how you model this language in F#.
Listing 12-1. A Minimalistic Representation of Propositional Logic
type Var = string
type Prop =
| And of Prop * Prop
| Var of Var
| Not of Prop
| Exists of Var * Prop
| False
let True = Not False
let Or(p, q) = Not(And(Not(p), Not(q)))
let Iff(p, q) = Or(And(p, q), And(Not(p), Not(q)))
let Implies(p, q) = Or(Not(p), q)
let Forall(v, p) = Not(Exists(v, Not(p)))
let (&&&) p q = And(p, q)
let (|||) p q = Or(p, q)
let (~~~) p = Not p
let (<=>) p q = Iff(p, q)
let (===) p q = (p <=> q)
let (==>) p q = Implies(p, q)
let (^^^) p q = Not (p <=> q)
let var (nm: Var) = Var nm
let fresh =
let count = ref 0
fun nm -> incr count; (sprintf "_%s%d" nm !count : Var)
Listing 12-1 uses a minimalistic encoding of propositional logic terms, where True, Or, Iff, Implies, and Forall are derived constructs, defined using their standard classical definitions in terms of the primitives Var, And, Not, Exists, and False. This is adequate for your purposes because you aren’t so interested in preserving the original structure of formulae; if you do need to display a symbolic propositional formula, you’re happy to display a form different than the original input.
Variables in formulae of type Prop are primitive propositions. A primitive proposition is often used to model some real-world possibility. For example, “it is raining,” “it is cold,” and “it is snowing” can be represented by Var("raining"), Var("cold"), and Var("snowing"). A Prop formula may be a tautology—that is, something that is always true regardless of the interpretation of these primitives. A formula is satisfiable if there is at least one interpretation for which it’s true. A formula can also be an axiom; for example, “if it’s snowing, then it’s cold” can be represented as the assumption Implies(Var("snowing"), Var("cold")). In this example, variables are used to represent a wire in a digital circuit that may be low or high.
When you’re dealing directly with the abstract syntax for Prop, it can be convenient to define infix operators to help you build abstract syntax values. Listing 12-1 shows the definition of seven operators (&&&, |||, ~~~, <=>, ===, ==>, and ^^^) that look a little like the notation you expect for propositional logic. You also define the function var for building primitive propositions and fresh for generating fresh variables. The types of these functions are as follows:
val var : nm:Var -> Prop
val fresh : (string -> Var)
Note The operators in Listing 12-1 aren’t overloaded and indeed outscope the default overloaded bitwise operations on integers discussed in Chapter 3. However, that doesn’t matter for the purposes of this chapter. If necessary, you can use alternative operator names.
Evaluating Propositional Logic Naively
Before tackling the problem of representing hardware using propositional logic, let’s look at some naive approaches for working with propositional logic formulae. Listing 12-2 shows routines that evaluate formulae given an assignment of variables and that generate the rows of a truth table for a Prop formula.
Listing 12-2. Evaluating Propositional Logic Formulae
let rec eval (env: Map<Var,bool>) inp =
match inp with
| Exists(v, p) -> eval (env.Add(v, false)) p || eval (env.Add(v, true)) p
| And(p1, p2) -> eval env p1 && eval env p2
| Var v -> if env.ContainsKey(v) then env.[v]
else failwithf "env didn't contain a value for %A" v
| Not p -> not (eval env p)
| False -> false
let rec support f =
match f with
| And(x, y) -> Set.union (support x) (support y)
| Exists(v, p) -> (support p).Remove(v)
| Var p -> Set.singleton p
| Not x -> support x
| False -> Set.empty
let rec cases supp =
seq {
match supp with
| [] -> yield Map.empty
| v :: rest ->
yield! rest |> cases |> Seq.map (Map.add v false)
yield! rest |> cases |> Seq.map (Map.add v true)
}
let truthTable x =
x |> support |> Set.toList |> cases
|> Seq.map (fun env -> env, eval env x)
let satisfiable x =
x |> truthTable |> Seq.exists (fun (env, res) -> res)
let tautology x =
x |> truthTable |> Seq.forall (fun (env, res) -> res)
let tautologyWithCounterExample x =
x |> truthTable |> Seq.tryFind (fun (env, res) -> not res)
|> Option.map fst
let printCounterExample = function
| None -> printfn "tautology verified OK"
| Some env -> printfn "tautology failed on %A" (Seq.toList env)
The types of these functions are as follows:
val eval : env:Map<Var,bool> -> inp:Prop -> bool
val support : f:Prop -> Set<Var>
val cases : supp:'a list -> seq<Map<'a,bool>> when 'a : comparison
val truthTable : x:Prop -> seq<Map<Var,bool> * bool>
val satisfiable : x:Prop -> bool
val tautology : x:Prop -> bool
val tautologyWithCounterExample : x:Prop -> Map<Var,bool> option
val printCounterExample : _arg1:#seq<'b> option -> unit
The function eval computes the value of a formula given assignments for each of the variables that occurs in the formula. support computes the set of variables that occurs in the formula. You can now use these functions to examine truth tables for some simple formulae, although first you may want to define the following functions to display truth tables neatly in F# Interactive:
let stringOfBit b = if b then "T" else "F"
let stringOfEnv env =
Map.fold (fun acc k v -> sprintf "%s=%s;" k (stringOfBit v) + acc) "" env
let stringOfLine (env, res) =
sprintf "%20s %s" (stringOfEnv env) (stringOfBit res)
let stringOfTruthTable tt =
"
" + (tt |> Seq.toList |> List.map stringOfLine |> String.concat "
")
Here are the truth tables for x, x AND y, and x OR NOT(x):
> fsi.AddPrinter(fun tt -> tt |> Seq.truncate 20 |> stringOfTruthTable);;
> truthTable (var "x");;
val it : seq<Map<Var,bool> * bool> =
x=F; F
x=T; T
> truthTable (var "x" &&& var "y");;
val it : seq<Map<Var,bool> * bool> =
y=F;x=F; F
y=T;x=F; F
y=F;x=T; F
y=T;x=T; T
> truthTable (var "x" ||| ~~~(var "x"));;
val it : seq<Map<Var,bool> * bool> =
x=F; T
From this, you can see that x OR NOT(x) is a tautology, because it always evaluates to TRUE regardless of the value of the variable x.
From Circuits to Propositional Logic
Figure 12-1 shows a diagrammatic representation of three hardware circuits: a half adder, a full adder, and a 2-bit carry ripple adder. The first of these has two input wires, x and y, and sets the sum wire high if exactly one of these is high. If both x and y are high, then the sum is low, and the carry wire is high instead. Thus, the circuit computes the 2-bit sum of the inputs. Likewise, a full adder computes the sum of three Boolean inputs, which, because it’s at most three, can still be represented by 2 bits. A 2-bit carry ripple adder is formed by composing a half adder and a full adder together, wiring the carry from the first adder to one of the inputs of the second adder. The overall circuit has four inputs and three outputs.
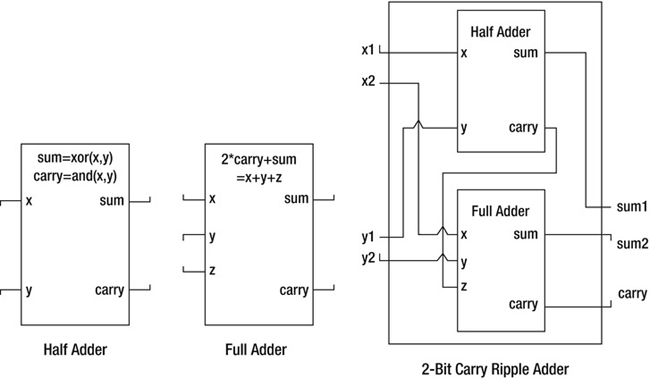
Figure 12-1. Three simple hardware circuits
The following code models these circuit components. This uses relational modeling, where each circuit is modeled not as a function but as a propositional logic predicate that relates its input wires to its output wires:
let sumBit x y = (x ^^^ y)
let carryBit x y = (x &&& y)
let halfAdder x y sum carry =
(sum === sumBit x y) &&&
(carry === carryBit x y)
let fullAdder x y z sum carry =
let xy = (sumBit x y)
(sum === sumBit xy z) &&&
(carry === (carryBit x y ||| carryBit xy z))
let twoBitAdder (x1, x2) (y1, y2) (sum1, sum2) carryInner carry =
halfAdder x1 y1 sum1 carryInner &&&
fullAdder x2 y2 carryInner sum2 carry
Note the close relation between the diagram for the 2-bit adder and its representation as code. You can read the implementation as a specification of the diagram, and vice versa. But the types of these functions are a little less informative:
val sumBit : x:Prop -> y:Prop -> Prop
val carryBit : x:Prop -> y:Prop -> Prop
val halfAdder : x:Prop -> y:Prop -> sum:Prop -> carry:Prop -> Prop
val fullAdder : x:Prop -> y:Prop -> z:Prop -> sum:Prop -> carry:Prop -> Prop
val twoBitAdder :
x1:Prop * x2:Prop ->
y1:Prop * y2:Prop ->
sum1:Prop * sum2:Prop -> carryInner:Prop -> carry:Prop -> Prop
In practice, circuits are defined largely with respect to vectors of wires, not just individual wires. You can model these using arrays of propositions; and because it’s now clear that you’re modeling bits via propositions, you make an appropriate type abbreviation for them as well:
type bit = Prop
type bitvec = bit[]
let Lo : bit = False
let Hi : bit = True
let vec n nm : bitvec = Array.init n (fun i -> var (sprintf "%s%d" nm i))
let bitEq (b1: bit) (b2: bit) = (b1 <=> b2)
let AndL l = Seq.reduce (fun x y -> And(x, y)) l
let vecEq (v1: bitvec) (v2: bitvec) = AndL (Array.map2 bitEq v1 v2)
These functions have types as follows:
type bit = Prop
type bitvec = bit []
val Lo : bit = False
val Hi : bit = Not False
val vec : n:int -> nm:string -> bitvec
val bitEq : b1:bit -> b2:bit -> Prop
val AndL : l:seq<Prop> -> Prop
val vecEq : v1:bitvec -> v2:bitvec -> Prop
You can now proceed to define larger circuits. For example:
let fourBitAdder (x: bitvec) (y: bitvec) (sum: bitvec) (carry: bitvec) =
halfAdder x.[0] y.[0] sum.[0] carry.[0] &&&
fullAdder x.[1] y.[1] carry.[0] sum.[1] carry.[1] &&&
fullAdder x.[2] y.[2] carry.[1] sum.[2] carry.[2] &&&
fullAdder x.[3] y.[3] carry.[2] sum.[3] carry.[3]
Or, more generally, you can chain an arbitrary series of adders to form an N-bit adder. First you define an abbreviation for the AndL function to represent the composition of multiple circuit blocks:
let Blocks l = AndL l
And here is the definition of an N-bit adder with a halfAdder at one end:
let nBitCarryRippleAdder (n: int) (x: bitvec) (y: bitvec)
(sum: bitvec) (carry: bitvec) =
Blocks [ for i in 0 .. n-1 ->
if i = 0
then halfAdder x.[i] y.[i] sum.[i] carry.[i]
else fullAdder x.[i] y.[i] carry.[i-1] sum.[i] carry.[i] ]
Using a similar approach, you get the following satisfying specification of a symmetric N-bit adder that accepts a carry as input and also gives a carry as output:
let rippleAdder (n: int) (x: bitvec) (y: bitvec)
(sum: bitvec) (carry: bitvec) =
Blocks [ for i in 0 .. n-1 ->
fullAdder x.[i] y.[i] carry.[i] sum.[i] carry.[i+1] ]
Let’s now look at the propositional formula for a halfAdder with variable inputs and outputs:
> halfAdder (var "x") (var "y") (var "sum") (var "carry");;
val it : Prop =
And
(Not
(And
(Not
(And
(Var "sum",
Not
(Not
(And
(Not (And (Var "x",Var "y")),
Not (And (Not (Var "x"),Not (Var "y")))))))),
Not
(And
(Not (Var "sum"),
Not
(Not
(Not
(And
(Not (And (Var "x",Var "y")),
Not (And (Not (Var "x"),Not (Var "y"))))))))))),
Not
(And
(Not (And (Var "carry",And (Var "x",Var "y"))),
Not (And (Not (Var "carry"),Not (And (Var "x",Var "y")))))))
Clearly, you don’t want to be doing too much of that! You see better ways of inspecting circuits and the symbolic values of bit vectors in the section “Representing Propositional Formulae Efficiently Using BDDs.”
In passing, note that the twoBitAdder uses an internal wire. You can model this using an existential formula:
let twoBitAdderWithHiding (x1, x2) (y1, y2) (sum1, sum2) carry =
let carryInnerVar = fresh "carry"
let carryInner = var(carryInnerVar)
Exists(carryInnerVar, halfAdder x1 y1 sum1 carryInner &&&
fullAdder x2 y2 carryInner sum2 carry)
However, this brings up issues beyond the scope of this chapter. Instead, you take an approach to modeling where there are no boundaries to the circuits and where all internal wires are exposed.
Checking Simple Properties of Circuits
Now that you’ve modeled the initial hardware circuits, you can check simple properties of these circuits. For example, you can check that if you give a fullAdder all low (that is, false) inputs, then the output wires may be low as well, and, conversely, that you have a contradiction if one of the output wires is high:
> tautology (fullAdder Lo Lo Lo Lo Lo);;
val it : bool = true
> satisfiable (fullAdder Lo Lo Lo Hi Lo);;
val it : bool = false
It’s of course much better to check these results symbolically by giving symbolic inputs. For example, you can check that if the same value is given to the two inputs of a halfAdder, then the sum output is low and the carry output is the same as the input:
> tautology (halfAdder (var "x") (var "x") Lo (var "x"));;
val it : bool = true
Likewise, you can check that a 2-bit adder is commutative—in other words, that it doesn’t matter if you swap the x and y inputs:
> tautology
(nBitCarryRippleAdder 2 (vec 2 "x") (vec 2 "y") (vec 2 "sum") (vec 3 "carry")
=== nBitCarryRippleAdder 2 (vec 2 "y") (vec 2 "x") (vec 2 "sum") (vec 3 "carry"));;
val it : bool = true
However, if you repeat the same for sizes of 5 or bigger, things start to slow down, and the naive implementation of checking propositional logic tautology based on truth tables begins to break down. Hence, you have to turn to more efficient techniques to process propositional formulae.
Representing Propositional Formulae Efficiently Using BDDs
In practice, propositional formulae to describe hardware can be enormous, involving hundreds of thousands of nodes. As a result, hardware companies have an interest in smart algorithms to process these formulae and check them for correctness. The circuits in the computers you use from day to day have almost certainly been verified using advanced propositional logic techniques, often using a functional language as the means to drive and control the analysis of the circuits.
A major advance in the application of symbolic techniques to hardware design occurred in the late 1980s with the discovery of binary decision diagrams, a representation for propositional logic formulae that is compact for many common circuit designs. BDDs represent a propositional formula via the use of if ... then ... else conditionals alone, which you write as (variable => true-branch | false-branch). Special nodes are used for true and false at the leaves: you write these as T and F. Every BDD is constructed with respect to a global variable ordering, so x AND NOT y can be represented as (x => (y => F | T) | F) if x comes before y in this ordering and as (y => F | (x => T | F)) if y comes before x. The variable ordering can be critical for performance of the representation.
BDDs are efficient because they use some of the language representation techniques you saw in Chapter 9. In particular, they work by uniquely memoizing all BDD nodes that are identical, which works by representing a BDD as an integer index into a lookup table that stores the real information about the node. Furthermore, negative indexes are used to represent the negation of a particular BDD node without creating a separate entry for the negated node. Listing 12-3 shows an implementation of BDDs. Fully polished BDD packages are often implemented in C. It’s easy to access those packages from F# using the techniques described in Chapter 19. Here, you have a clear and simple implementation entirely in F# code.
Listing 12-3. Implementing Binary Decision Diagrams
open System.Collections.Generic
let memoize f =
let tab = new Dictionary<_, _>()
fun x ->
if tab.ContainsKey(x) then tab.[x]
else let res = f x in tab.[x] <- res; res
type BddIndex = int
type Bdd = Bdd of BddIndex
type BddNode = Node of Var * BddIndex * BddIndex
type BddBuilder(order: Var -> Var -> int) =
// The core data structures that preserve uniqueness
let nodeToIndex = new Dictionary<BddNode, BddIndex>()
let indexToNode = new Dictionary<BddIndex, BddNode>()
// Keep track of the next index
let mutable nextIdx = 2
let trueIdx = 1
let falseIdx = -1
let trueNode = Node("", trueIdx, trueIdx)
let falseNode = Node("", falseIdx, falseIdx)
// Map indexes to nodes. Negative indexes go to their negation.
// The special indexes -1 and 1 go to special true/false nodes.
let idxToNode(idx) =
if idx = trueIdx then trueNode
elif idx = falseIdx then falseNode
elif idx > 0 then indexToNode.[idx]
else
let (Node(v, l, r)) = indexToNode.[-idx]
Node(v, -l, -r)
// Map nodes to indexes. Add an entry to the table if needed.
let nodeToUniqueIdx(node) =
if nodeToIndex.ContainsKey(node) then nodeToIndex.[node]
else
let idx = nextIdx
nodeToIndex.[node] <- idx
indexToNode.[idx] <- node
nextIdx <- nextIdx + 1
idx
// Get the canonical index for a node. Preserve the invariant that the
// left-hand node of a conditional is always a positive node
let mkNode(v: Var, l: BddIndex, r: BddIndex) =
if l = r then l
elif l >= 0 then nodeToUniqueIdx(Node(v, l, r) )
else -nodeToUniqueIdx(Node(v, -l, -r))
// Construct the BDD for a conjunction "m1 AND m2"
let rec mkAnd(m1, m2) =
if m1 = falseIdx || m2 = falseIdx then falseIdx
elif m1 = trueIdx then m2
elif m2 = trueIdx then m1
else
let (Node(x, l1, r1)) = idxToNode(m1)
let (Node(y, l2, r2)) = idxToNode(m2)
let v, (la, lb), (ra, rb) =
match order x y with
| c when c = 0 -> x, (l1, l2), (r1, r2)
| c when c < 0 -> x, (l1, m2), (r1, m2)
| c -> y, (m1, l2), (m1, r2)
mkNode(v, mkAnd(la, lb), mkAnd(ra, rb))
// Memoize this function
let mkAnd = memoize mkAnd
// Publish the construction functions that make BDDs from existing BDDs
member g.False = Bdd falseIdx
member g.And(Bdd m1, Bdd m2) = Bdd(mkAnd(m1, m2))
member g.Not(Bdd m) = Bdd(-m)
member g.Var(nm) = Bdd(mkNode(nm, trueIdx, falseIdx))
member g.NodeCount = nextIdx
The types of these functions are as follows:
val memoize : f:('a -> 'b) -> ('a -> 'b) when 'a : equality
type BddIndex = int
type Bdd = | Bdd of BddIndex
type BddNode = | Node of Var * BddIndex * BddIndex
type BddBuilder =
class
new : order:(Var -> Var -> int) -> BddBuilder
member And : Bdd * Bdd -> Bdd
member Not : Bdd -> Bdd
member Var : nm:Var -> Bdd
member False : Bdd
member NodeCount : int
end
In addition to the functions that ensure that nodes are unique, the only substantial function in the implementation is mkAnd. It relies on the following logical rules for constructing BDD nodes formed by taking the conjunction of existing nodes. Note how the second rule is used to interleave variables:
- (x => P | Q) AND (x => R | S) is identical to (x => P AND R | Q AND S).
- (x => P | Q) AND (y => R | S) is identical to (x => P AND T | Q AND T) where T is simply (y => R | S).
One final important optimization in the implementation is to memoize the application of the mkAnd operation.
Given the previous implementation of BDDs, you can now add the members ToString to convert BDDs to strings, Build to convert a Prop representation of a formula into a BDD, and Equiv to check for equivalence between two BDDs:
type BddBuilder(order: Var -> Var -> int) =
...
member g.ToString(Bdd idx) =
let rec fmt dep idx =
if dep > 3 then "..." else
let (Node(p, l, r)) = idxToNode(idx)
if p = "" then if l = trueIdx then "T" else "F"
else sprintf "(%s => %s | %s)" p (fmt (dep+1) l) (fmt (dep+1) r)
fmt 1 idx
member g.Build(f) =
match f with
| And(x, y) -> g.And(g.Build x, g.Build y)
| Var(p) -> g.Var(p)
| Not(x) -> g.Not(g.Build x)
| False -> g.False
| Exists(v, p) -> failwith "Exists node"
member g.Equiv(p1, p2) = g.Build(p1) = g.Build(p2))
You can now install a pretty-printer and inspect the BDDs for some simple formulae:
> let bddBuilder = BddBuilder(compare);;
val bddBuilder: BddBuilder
> fsi.AddPrinter(fun bdd -> bddBuilder.ToString(bdd));;
val it: unit = ()
> bddBuilder.Build(var "x");;
val it : Bdd = (x => T | F)
> bddBuilder.Build(var "x" &&& var "x");;
val it : Bdd = (x => T | F)
> bddBuilder.Build(var "x") = bddBuilder.Build(var "x" &&& var "x");;
val it : bool = true
> (var "x") = (var "x" &&& var "x");;
val it : bool = false
> bddBuilder.Build(var "x" &&& var "y");;
val it : Bdd = (x => (y => T | F) | F)
> bddBuilder.Equiv(var "x", var "x" &&& var "x");;
val it : bool = true
Note that the BDD representations of x and x AND x are identical, whereas the Prop representations aren’t. The Prop representation is an abstract syntax representation, whereas the BDD representation is more of a semantic or computational representation. The BDD representation incorporates all the logic necessary to prove propositional formula equivalent; in other words, this logic is built into the representation.
Circuit Verification with BDDs
You can now use BDDs to perform circuit verification. For example, the following verifies that you can swap the x and y inputs to an 8-bit adder:
> bddBuilder.Equiv(
nBitCarryRippleAdder 8 (vec 8 "x") (vec 8 "y") (vec 8 "sum") (vec 9 "carry"),
nBitCarryRippleAdder 8 (vec 8 "y") (vec 8 "x") (vec 8 "sum") (vec 9 "carry"));;
val it : bool = true
Thirty-three variables are involved in this circuit. A naive exploration of this space would involve searching a truth table of more than eight billion entries. The BDD implementation takes moments on any modern computer. Efficient symbolic representations pay off!
A more substantial verification problem involves checking the equivalence of circuits that have substantial structural differences. To explore this, let’s take a different implementation of addition called a carry select adder. This avoids a major problem with ripple adders caused by the fact that the carry signal must propagate along the entire length of the chain of internal adders, causing longer delays in the electrical signals and thus reducing the clock rates of a circuit or possibly increasing power consumption. A carry select adder gets around this through a common hardware trick of speculative execution. It divides the inputs into blocks and adds each block twice: once assuming the carry is low and once assuming it’s high. The result is then selected after the circuit, when the carry for the block has been computed. Listing 12-4 shows the specification of the essence of the hardware layout of a carry select adder using the techniques developed so far. The specification uses the slicing syntax for arrays described in Chapter 4.
Listing 12-4. A Carry Select Adder Modeled Using Propositional Logic
let mux a b c = ((~~~a ==> b) &&& (a ==> c))
let carrySelectAdder
totalSize maxBlockSize
(x: bitvec) (y: bitvec)
(sumLo: bitvec) (sumHi: bitvec)
(carryLo: bitvec) (carryHi: bitvec)
(sum: bitvec) (carry: bitvec) =
Blocks
[ for i in 0..maxBlockSize..totalSize-1 ->
let sz = min (totalSize-i) maxBlockSize
let j = i+sz-1
let carryLo = Array.append [| False |] carryLo.[i+1..j+1]
let adderLo = rippleAdder sz x.[i..j] y.[i..j] sumLo.[i..j] carryLo
let carryHi = Array.append [| True |] carryHi.[i+1..j+1]
let adderHi = rippleAdder sz x.[i..j] y.[i..j] sumHi.[i..j] carryHi
let carrySelect = (carry.[j+1] === mux carry.[i] carryLo.[sz] carryHi.[sz])
let sumSelect =
Blocks
[ for k in i..j ->
sum.[k] === mux carry.[i] sumLo.[k] sumHi.[k] ]
adderLo &&& adderHi &&& carrySelect &&& sumSelect ]
You can now check that a carrySelectAdder is equivalent to a rippleAdder. Here’s the overall verification condition:
let checkAdders n k =
let x = vec n "x"
let y = vec n "y"
let sumA = vec n "sumA"
let sumB = vec n "sumB"
let sumLo = vec n "sumLo"
let sumHi = vec n "sumHi"
let carryA = vec (n+1) "carryA"
let carryB = vec (n+1) "carryB"
let carryLo = vec (n+1) "carryLo"
let carryHi = vec (n+1) "carryHi"
let adder1 = carrySelectAdder n k x y sumLo sumHi carryLo carryHi sumA carryA
let adder2 = rippleAdder n x y sumB carryB
(adder1 &&& adder2 &&& (carryA.[0] === carryB.[0]) ==>
(vecEq sumA sumB &&& bitEq carryA.[n] carryB.[n]))
Ignoring the construction of the inputs, the verification condition specifies the following:
- Assume you have the two adder circuits, with the same inputs.
- Assume the input
carrybits are the same.- Then, the output
sumvectors are identical, and the final outputcarrybits are identical.
Here is the verification condition being checked interactively, for 5-bit inputs, in chunks of 2 for the carrySelectAdder:
In practice, BDDs require a good variable ordering, and the default alphabetic ordering is unlikely to be the best. Here is a larger verification using a more random ordering induced by first comparing on the hash codes of the names of the variables:
let approxCompareOn f x y =
let c = compare (f x) (f y)
if c <> 0 then c else compare x y
let bddBuilder2 = BddBuilder(approxCompareOn hash)> bddBuilder2.Equiv(checkAdders 7 2, True);;
val it : bool = true
Seventy-four Boolean variables are involved in this last verification problem. You would have to generate up to 274 test cases to explore this systematically via testing; that’s 22 thousand billion billion test cases. By using symbolic techniques, you’ve explored this entire space in a matter of seconds and in only a few hundred lines of code.
Note Hardware and software verification are highly active areas of research and one of the most important applications of symbolic programming techniques in the industrial arena. The verifications performed here aim to give you a taste of how symbolic techniques can provide nontrivial results about circuits in a matter of seconds. We’ve omitted some simple techniques that can make these verifications scale to very large circuits; for example, we expand equivalence nodes in propositional formulae. Preserving them can lead to smaller symbolic descriptions and more efficient processing with BDDs.
Symbolic Differentiation and Expression Rendering
You’ve probably come across the need to perform symbolic differentiation one way or another; and unless you had access to a full-fledged mathematics application such as Maple, Matlab or Mathematica, you had to resort to working out the math yourself on paper. This no longer has to be the case, because you can develop your own symbolic differentiation tool in almost no time and with surprising brevity and clarity. Figure 12-2 shows the symbolic differentiation application that you will implement in this chapter.
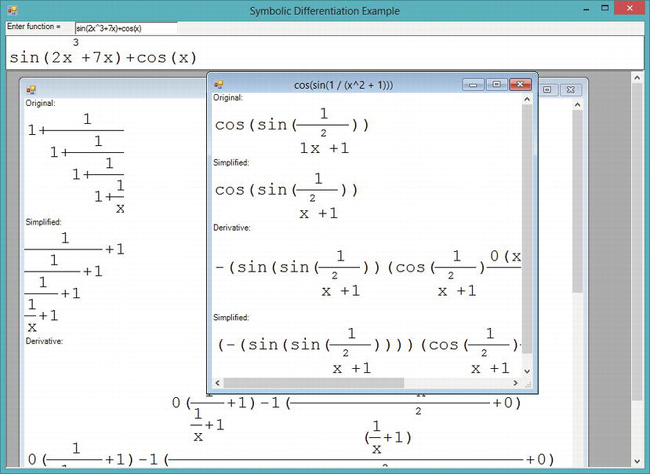
Figure 12-2. The visual symbolic differentiation application
Modeling Simple Algebraic Expressions
Let’s take it easy at first and assume you’re dealing with simple algebraic expressions that can consist only of numbers, a single variable (it doesn’t matter what it is, but let’s assume it’s x), sums, and products. Listing 12-5 shows the implementation of symbolic differentiation over this simple expression type.
Listing 12-5. Symbolic Differentiation Over a Simple Expression Type
open System
type Expr =
| Var
| Num of int
| Sum of Expr * Expr
| Prod of Expr * Expr
let rec deriv expr =
match expr with
| Var -> Num 1
| Num _ -> Num 0
| Sum (e1, e2) -> Sum (deriv e1, deriv e2)
| Prod (e1, e2) -> Sum (Prod (e1, deriv e2), Prod (e2, deriv e1))
The type of the deriv function is as follows:
val deriv : expr:Expr -> Expr
Now, let’s find the derivative of a simple expression, say 1+2x:
> let e1 = Sum (Num 1, Prod (Num 2, Var));;
val e1 : Expr = Sum (Num 1,Prod (Num 2,Var))
> deriv e1;;
val it : Expr = Sum (Num 0,Sum (Prod (Num 2,Num 1),Prod (Var,Num 0)))
The resulting expression is a symbolic representation of 0+(2*1+x*0), which indeed is 2— so it’s right. You should do a couple of things next. First, install a custom printer so that F# Interactive responds using expressions that you’re more used to using. Before you apply brute force and put parentheses around the expressions in each sum and product, let’s contemplate it a bit. Parentheses are usually needed to give precedence to operations that would otherwise be applied later in the sequence of calculations. For instance, 2+3*4 is calculated as 2+(3*4) because the product has a higher precedence; if you were to find (2+3)*4, you would need to use parentheses to designate the new order of calculation. Taking this argument further, you can formulate the rule for using parentheses: they’re needed in places where an operator has lower precedence than the one surrounding it. You can apply this reasoning to the expression printer by passing a context precedence parameter:
let precSum = 10
let precProd = 20
let rec stringOfExpr prec expr =
match expr with
| Var -> "x"
| Num i -> i.ToString()
| Sum (e1, e2) ->
let sum = stringOfExpr precSum e1 + "+" + stringOfExpr precSum e2
if prec > precSum then
"(" + sum + ")"
else
sum
| Prod (e1, e2) ->
stringOfExpr precProd e1 + "*" + stringOfExpr precProd e2
You can add this as a custom printer for this expression type:
> fsi.AddPrinter (fun expr -> stringOfExpr 0 expr);;
val it : unit = ()
> let e3 = Prod (Var, Prod (Var, Num 2));;
val e3 : Expr = x*x*2
> deriv e3;;
val it : Expr = x*(x*0+2*1)+x*2*1
Parentheses are omitted only when a sum is participating in an expression that has a higher precedence, which in this simplified example means products. If you didn’t add precedence to the pretty-printer, you’d get x*x*0+2*1+x*2*1 for the last expression, which is incorrect.
Implementing Local Simplifications
The next thing to do is to get your symbolic manipulator to simplify expressions so you don’t have to do so. One easy modification is to replace the use of the Sum and Prod constructors in deriv with local functions that perform local simplifications such as removing identity operations, performing arithmetic, bringing forward constants, and simplifying across two operations. Listing 12-6 shows how to do this.
Listing 12-6. Symbolic Differentiation with Local Simplifications
let simpSum = function
| Num n, Num m -> Num (n+m) // constants!
| Num 0, e | e, Num 0 -> e // 0+e = e+0 = e
| e1, e2 -> Sum(e1, e2)
let simpProd = function
| Num n, Num m -> Num (n*m) // constants!
| Num 0, e | e, Num 0 -> Num 0 // 0*e=0
| Num 1, e | e, Num 1 -> e // 1*e = e*1 = e
| e1, e2 -> Prod(e1, e2)
let rec simpDeriv = function
| Var -> Num 1
| Num _ -> Num 0
| Sum (e1, e2) -> simpSum (simpDeriv e1, simpDeriv e2)
| Prod (e1, e2) -> simpSum (simpProd (e1, simpDeriv e2),
simpProd (e2, simpDeriv e1))
These measures produce significant improvement over the previous naive approach, but they don’t place the result in a normal form, as the following shows:
> simpDeriv e3;;
val it : Expr = x*2+x*2
However, you can’t implement all simplifications using local rules; for example, collecting like terms across a polynomial involves looking at every term of the polynomial.
Note Listing 12-6 uses the expression form function pattern-rules -> expression. This is equivalent to (fun x -> match x with pattern-rules -> expression) and is especially convenient as a way to define functions working directly over discriminated unions.
A Richer Language of Algebraic Expressions
This section goes beyond the approach presented so far and shows how to develop a UI application that can accept algebraic expressions as input and simplify, differentiate, and render them graphically. Figure 12-3 shows the project structure. To run this example, you will need to install the F# PowerPack, a collection of useful F# tools and libraries available at http://fsharppowerpack.codeplex.com; and add library references to FSharp.PowerPack from the F# PowerPack and System.Windows.Forms from the standard .NET libraries. For convenience, you can add the lexer ExprLexer.fsl and the parser ExprParser.fsy to the project so you can quickly edit them if necessary. You can manually include a reference to the F# PowerPack targets in the project file to automatically generate code for the parser and lexer definitions, or you can manually generate these files. You do the latter for this example, but in both cases you need to add the generated files (ExprParser.fs and ExprLexer.fs) to the project.
The main Expr type that represents algebraic expressions is contained in Expr.fs. Although you can use the expression constructors defined in this type to create expression values on the fly, the most convenient method for embedding complex expressions into this representation is by parsing them.
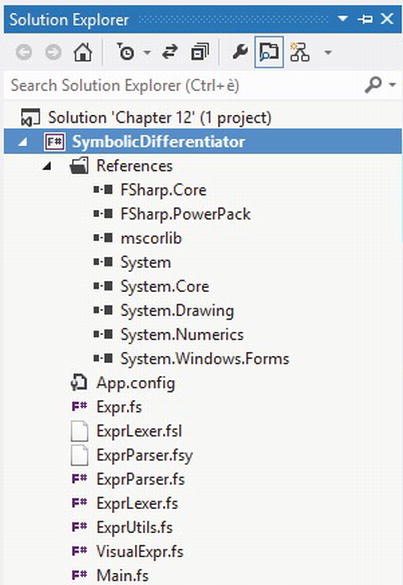
Figure 12-3. The Symbolic Differentiation Solution in Visual Studio 2012
Armed with the ability to encode and parse algebraic expressions, you place the derivation and simplification logic in its own module and file (ExprUtil.fs). The last piece is rendering (in VisualExpr.fs). Finally, a simple UI client in Main.fs completes the application.
Listing 12-7 shows the definition of the abstract syntax representation of expressions using a single Expr type. Expressions contain numbers, variables, negation, sums, differences, products, fractions, exponents, basic trigonometric functions (sin x, cos x), and ex.
Let’s look at this abstract syntax design more closely. In Chapter 9, you saw that choosing an abstract syntax often involves design choices, and that these choices often relate to the roles the abstract syntax representation should serve. In this case, you use the abstract syntax to compute symbolic derivatives and simplifications (using techniques similar to those earlier in this chapter) and also to graphically visualize the resulting expressions in a way that is pleasant for the human user. For this reason, you don’t use an entirely minimalistic abstract syntax (for example, by replacing quotients with an inverse node), because it’s helpful to maintain some additional structure in the input.
Here, you represent sums and differences not as binary terms (as you do for products and quotients) but instead as a list of expression terms. The Sub term also carries the minuend, the term that is to be reduced, separately. As a result, you have to apply different strategies when simplifying them.
Listing 12-7. Expr.fs: The Core Expression Type for the Visual Symbolic Differentiation Application
namespace Symbolic.Expressions
type Expr =
| Num of decimal
| Var of string
| Neg of Expr
| Add of Expr list
| Sub of Expr * Expr list
| Prod of Expr * Expr
| Frac of Expr * Expr
| Pow of Expr * decimal
| Sin of Expr
| Cos of Expr
| Exp of Expr
static member StarNeeded e1 e2 =
match e1, e2 with
| Num _, Neg _ | _, Num _ -> true
| _ -> false
member self.IsNumber =
match self with
| Num _ -> true | _ -> false
member self.NumOf =
match self with
| Num num -> num | _ -> failwith "NumOf: Not a Num"
member self.IsNegative =
match self with
| Num num | Prod (Num num, _) -> num < 0M
| Neg e -> true | _ -> false
member self.Negate =
match self with
| Num num -> Num (-num)
| Neg e -> e
| exp -> Neg exp
Listing 12-7 also shows the definition of some miscellaneous augmentations on the expression type, mostly related to visual layout and presentation. The StarNeeded member is used internally to determine whether the multiplication operator (the star symbol, or asterisk) is needed in the product of two expressions, e1 and e2. You may want to extend this simple rule: any product whose right side is a number requires the explicit operator, and all other cases don’t. Thus, expressions such as 2(x+1) and 2x are rendered without the asterisk.
The IsNumber member returns true if the expression at hand is numeric and is used in conjunction with NumOf, which returns this numeric component. Similarly, the IsNegative and Negate members determine whether you have an expression that starts with a negative sign, and they negate it on demand.
Parsing Algebraic Expressions
This sample uses a lexer and a parser generated by the F# tools fsyacc.exe and fslex.exe, available as part of the F# PowerPack. This chapter skips over the details of how the tools work; instead it assumes that you have these tools installed. Listings 12-8 and 12-9 show the code for the lexer and parser. You need to manually build the lexer (generating ExprLexer.fs) and parser (generating ExprParser.fs) from the Windows command line as follows:
C:samples> fsyacc ExprParser.fsy --module ExprParser
C:samples> fslex ExprLexer.fsl --unicode
Listing 12-8. ExprLexer.fsl: Tokenizing the Concrete Syntax for Algebraic Expressions
{
module ExprLexer
open System
open Microsoft.FSharp.Text.Lexing
open ExprParser
let lexeme = LexBuffer<_>.LexemeString
let special lexbuf = function
| "+" -> PLUS | "-" -> MINUS
| "*" -> TIMES | "/" -> DIV
| "(" -> LPAREN | ")" -> RPAREN | "^" -> HAT
| _ -> failwith "Invalid operator"
let id lexbuf = function
| "sin" -> SIN | "cos" -> COS
| "e" -> E | id -> ID id
}
let digit = ['0'-'9']
let int = digit+
let float = int ('.' int)? (['e' 'E'] int)?
let alpha = ['a'-'z' 'A'-'Z']
let id = alpha+ (alpha | digit | ['_' '$'])*
let ws = ' ' | ' '
let nl = '
' | '
' '
'
let special = '+' | '-' | '*' | '/' | '(' | ')' | '^'
rule main = parse
| int { INT (Convert.ToInt32(lexeme lexbuf)) }
| float { FLOAT (Convert.ToDouble(lexeme lexbuf)) }
| id { id lexbuf (lexeme lexbuf) }
| special { special lexbuf (lexeme lexbuf) }
| ws | nl { main lexbuf }
| eof { EOF }
| _ { failwith (lexeme lexbuf) }
The parser has some syntactic sugar for polynomial terms, so it can parse 2x, 2x^3, or x^4 without requiring you to add an explicit multiplication after the coefficient.
Listing 12-9. ExprParser.fsy: Parsing the Concrete Syntax for Algebraic Expressions
%{
open System
open Symbolic.Expressions
%}
%token <int> INT
%token <float> FLOAT
%token <string> ID
%token EOF LPAREN RPAREN PLUS MINUS TIMES DIV HAT SIN COS E
%left ID
%left prec_negate
%left LPAREN
%left PLUS MINUS
%left TIMES DIV
%left HAT
%start expr
%type <Expr> expr
%%
expr:
| exp EOF { $1 }
number:
| INT { Convert.ToDecimal($1) }
| FLOAT { Convert.ToDecimal($1) }
| MINUS INT %prec prec_negate { Convert.ToDecimal(-$2) }
| MINUS FLOAT %prec prec_negate { Convert.ToDecimal(-$2) }
exp:
| number { Num $1 }
| ID { Var $1 }
| exp PLUS exp { Add [$1; $3] }
| exp MINUS exp { Sub ($1, [$3]) }
| exp TIMES exp { Prod ($1, $3) }
| exp DIV exp { Frac ($1, $3) }
| SIN LPAREN exp RPAREN { Sin $3 }
| COS LPAREN exp RPAREN { Cos $3 }
| E HAT exp { Exp $3 }
| term { $1 }
| exp HAT number { Pow ($1, $3) }
| LPAREN exp RPAREN { $2 }
| MINUS LPAREN exp RPAREN { Neg $3 }
term:
| number ID { Prod (Num $1, Var $2) }
| number ID HAT number { Prod (Num $1, Pow (Var $2, $4)) }
| ID HAT number { Prod (Num 1M, Pow (Var $1, $3)) }
Simplifying Algebraic Expressions
At the start of this chapter, you simplified expressions using local techniques, but you also saw the limitations of this approach. Listing 12-10 shows a more complete implementation of a separate function (Simplify) that performs some nonlocal simplifications as well. Both this function and the one for derivation shown in the subsequent section are placed in a separate file (ExprUtil.fs).
Simplify uses two helper functions (collect and negate). The former collects constants from products using a bottom-up strategy that reduces constant subproducts and factors out constants by bringing them outward (to the left). Recall that product terms are binary.
Listing 12-10. ExprUtils.fs: Simplifying Algebraic Expressions
module Symbolic.Expressions.Utils
open Symbolic.Expressions
/// A helper function to map/select across a list while threading state
/// through the computation
let selectFold f l s =
let l,s' = List.fold
(fun (l',s') x ->
let x',s'' = f x s'
(List.rev x') @ l',s'')
([],s) l
List.rev l,s'
/// Collect constants
let rec collect = function
| Prod (e1, e2) ->
match collect e1, collect e2 with
| Num num1, Num num2 -> Num (num1 * num2)
| Num n1, Prod (Num n2, e)
| Prod (Num n2, e), Num n1 -> Prod (Num (n1 * n2), e)
| Num n, e | e, Num n -> Prod (Num n, e)
| Prod (Num n1, e1), Prod (Num n2, e2) ->
Prod (Num (n1 * n2), Prod (e1, e2))
| e1', e2' -> Prod (e1', e2')
| Num _ | Var _ as e -> e
| Neg e -> Neg (collect e)
| Add exprs -> Add (List.map collect exprs)
| Sub (e1, exprs) -> Sub (collect e1, List.map collect exprs)
| Frac (e1, e2) -> Frac (collect e1, collect e2)
| Pow (e1, num) -> Pow (collect e1, num)
| Sin e -> Sin (collect e)
| Cos e -> Cos (collect e)
| Exp _ as e -> e
/// Push negations through an expression
let rec negate = function
| Num num -> Num (-num)
| Var v as exp -> Neg exp
| Neg e -> e
| Add exprs -> Add (List.map negate exprs)
| Sub _ -> failwith "unexpected Sub"
| Prod (e1, e2) -> Prod (negate e1, e2)
| Frac (e1, e2) -> Frac (negate e1, e2)
| exp -> Neg exp
/// Simplify an expression
let rec simp = function
| Num num -> Num num
| Var v -> Var v
| Neg e -> negate (simp e)
| Add exprs ->
let filterNums (e:Expr) n =
if e.IsNumber
then [], n + e.NumOf
else [e], n
let summands = function | Add es -> es | e -> [e]
let exprs', num =
selectFold (simp >> summands >> selectFold filterNums) exprs 0M
match exprs' with
| [Num _ as n] when num = 0M -> n
| [] -> Num num
| [e] when num = 0M -> e
| _ when num = 0M -> Add exprs'
| _ -> Add (exprs' @ [Num num])
| Sub (e1, exprs) ->
simp (Add (e1 :: List.map Neg exprs))
| Prod (e1, e2) ->
match simp e1, simp e2 with
| Num num, _ | _, Num num when num = 0M -> Num 0M
| Num num, e | e, Num num when num = 1M -> e
| Num num1, Num num2 -> Num (num1 * num2)
| e1, e2 -> Prod (e1, e2)
| Frac (e1, e2) ->
match simp e1, simp e2 with
| Num num, _ when num = 0M -> Num num
| e1, Num num when num = 1M -> e1
| Num (_ as num), Frac (Num (_ as num2), e) ->
Prod (Frac (Num num, Num num2), e)
| Num (_ as num), Frac (e, Num (_ as num2)) ->
Frac (Prod (Num num, Num num2), e)
| e1, e2 -> Frac (e1, e2)
| Pow (e, n) when n=1M -> simp e
| Pow (e, n) -> Pow (simp e, n)
| Sin e -> Sin (simp e)
| Cos e -> Cos (simp e)
| Exp e -> Exp (simp e)
let Simplify e = e |> simp |> simp |> collect
The main simplification algorithm works as follows:
- Constants and variables are passed through verbatim. You use
negatewhen simplifying a negation, which assumes the expression at hand no longer contains differences and that sums were flattened (see the next item in this list).- Sums are traversed and nested sums are flattened, at the same time all constants are collected and added up. This reduces the complexity of further simplification considerably.
- Differences are converted to sums: for instance, A-B-C is converted to A+(-B)+(-C). Thus, the first element is preserved without negation.
- When simplifying a product, you first simplify its factors, and then you remove identity operations (multiplying by zero or one) and reduce products of constants.
- Fractions are handled similarly. Zero divided by anything is 0, anything divided by 1 is itself, and multiline fractions can be collapsed if you find numeric denominators or numerators.
- The rest of the match cases deal with simplifying subexpressions.
Symbolic Differentiation of Algebraic Expressions
Applying symbolic differentiation is a straightforward translation of the mathematical rules of differentiation into code. You could use local functions that act as constructors and perform local simplifications, but with the simplification function described earlier, this isn’t needed. Listing 12-11 shows the implementation of symbolic differentiation for the Expr type. Note how beautifully and succinctly the code follows the math behind it: the essence of the symbolic processing is merely 20 lines of code!
Listing 12-11. ExprUtil.fs (continued): Symbolic Differentiation for Algebraic Expressions
let Differentiate v e =
let rec diff v = function
| Num num -> Num 0M
| Var v' when v'=v -> Num 1M
| Var v' -> Num 0M
| Neg e -> diff v (Prod ((Num -1M), e))
| Add exprs -> Add (List.map (diff v) exprs)
| Sub (e1, exprs) -> Sub (diff v e1, List.map (diff v) exprs)
| Prod (e1, e2) -> Add [Prod (diff v e1, e2); Prod (e1, diff v e2)]
| Frac (e1, e2) ->
Frac (Sub (Prod (diff v e1, e2), [Prod (e1, diff v e2)]),
Pow (e2, 2M))
| Pow (e1, num) ->
Prod (Prod (Num num, Pow (e1, num - 1M)), diff v e1)
| Sin e -> Prod (Cos e, diff v e)
| Cos e -> Neg (Prod (Sin e, diff v e))
| Exp (Var v') as e when v'=v -> e
| Exp (Var v') as e when v'<>v -> Num 0M
| Exp e -> Prod (Exp e, diff v e)
diff v e
Rendering Expressions
Now that you have the basic machinery to easily parse, simplify, and differentiate expressions, you can start looking into how to visualize them to really enjoy the benefits of the application. The rendering engine (placed in VisualExpr.fs) has two main parts: converting expressions to VisualExpr values and then rendering them directly. Ideally, you should hide the representation of the VisualExpr (and its related VisualElement) type with a signature (not shown here) so that it isn’t possible to construct these values directly.
Before you get to the conversion and rendering functions, you need to do a bit of setup. To control how the different parts of an expression are rendered on the screen, you introduce the RenderOptions type containing the fonts and pen (which determines the color used to draw) that are applied during rendering. Listing 12-12 shows the code that defines the rendering options used in the remainder of this example.
Listing 12-12. VisualExpr.fs: Rendering Options for the Visual Symbolic Differentiation Application
namespace Symbolic.Expressions.Visual
open Symbolic.Expressions
open System.Drawing
open System.Drawing.Imaging
type RenderOptions =
{ NormalFont: Font; SmallFont: Font; IsSuper: bool; Pen: Pen; }
static member Default =
{
NormalFont = new Font("Courier New", 18.0f, FontStyle.Regular)
SmallFont = new Font("Courier New", 12.0f, FontStyle.Regular)
IsSuper = false
Pen = new Pen(Color.Black, 1.0f)
}
member self.Brush =
(new SolidBrush(Color.FromArgb(255, self.Pen.Color)) :> Brush)
Each algebraic expression is converted to a VisualExpr value as part of the rendering process. This ensures that you don’t have to deal with the variety of expression forms but only with a small set of simple shapes that can be rendered according to a few simple rules. These simpler building blocks are defined in the VisualElement type and shown in Listing 12-13. For instance, there are no sums or products; these and similar expressions are broken down into sequences of symbols (such as 1, x, and +). The two other visual elements are exponentiation and fractions, which are used to guide the display logic later during the rendering phase. Each visual element carries a size value that is calculated using a given set of rendering options.
Listing 12-13. VisualExpr.fs (continued): Visual Elements and Sizes for the Visual Symbolic Differentiation Application
type VisualElement =
| Symbol of string * ExprSize
| Power of VisualElement * VisualElement * ExprSize
| Sequence of VisualElement list * ExprSize
| Fraction of VisualElement * VisualElement * ExprSize
member self.Size =
match self with
| Symbol (_, size) | Power (_, _, size)
| Sequence (_, size) | Fraction (_, _, size) -> size
member self.Height = self.Size.Height
member self.Width = self.Size.Width
member self.Midline = self.Size.Midline
and ExprSize =
{ Width: int; Height: int; Midline: int; }
member self.CenterOnMidline size x y =
x + (size.Width-self.Width)/2, y + (size.Midline-self.Midline)
member self.Frac size opt =
{
Width = max self.Width size.Width
Height = self.Height + size.Height + self.FracSepHeight opt
Midline = self.Height + (self.FracSepHeight opt)/2
}
member self.FracSepHeight (opt: RenderOptions) =
max (int (opt.Pen.Width * 5.0f)) 4
member self.AddPower (e: VisualElement) =
{
Width = self.Width + e.Width
Height = self.Height + e.Height
Midline = self.Midline + e.Height
}
static member ExpandOne (size: ExprSize) (e: VisualElement) =
{
Width = size.Width + e.Width
Height = max size.Height e.Height
Midline = max size.Midline e.Midline
}
member self.Expand (exprs: VisualElement list) =
List.fold ExprSize.ExpandOne self exprs
static member Seq (exprs: VisualElement list) =
List.fold ExprSize.ExpandOne ExprSize.Zero exprs
static member Zero =
{ Width=0; Height=0; Midline=0; }
The size value encodes the dimensions (width and height in pixels) of the related visual expression and is managed through the ExprSize type, which provides various members to compute precise dimensions. Basically, this type handles the gory details of putting together small visuals to compose a large expression and manages how and where these small visuals should be placed. The main guideline is to align these visuals on a line (measured from the top of the expression in pixels and stored in the Midline field), as depicted in Figure 12-4.
The darker rectangles in this figure denote arbitrary expressions, whereas the lighter rectangles mark the dimensions of the parent expression aligned on the midline.
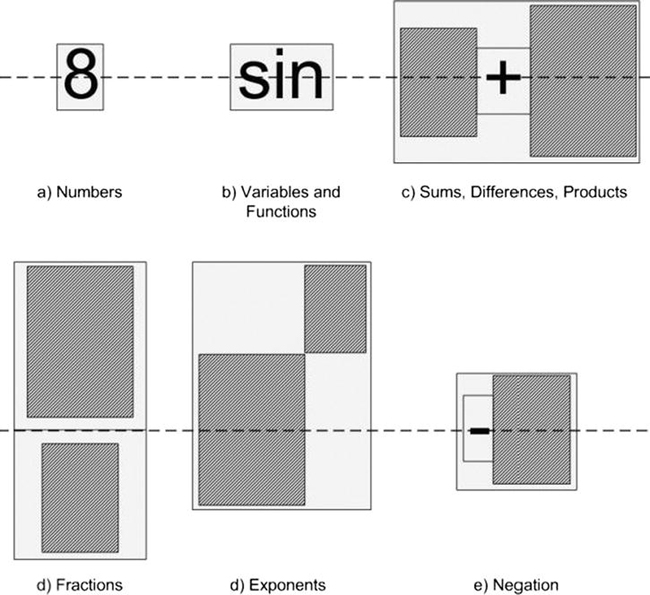
Figure 12-4. Expressions and their sizes
Converting to VisualExpr
Listing 12-14 shows the type VisualExpr that carries the main visual element and the rendering options that were used to produce it. This type also provides the method OfExpr to build a VisualExpr from an Expr.
Listing 12-14. VisualExpr.fs (continued): Visual Expressions for the Visual Symbolic Differentiation Application
type VisualExpr =
{ Expression : VisualElement; RenderOptions: RenderOptions; }
static member OfExpr (opt: RenderOptions) e =
use bmp = new Bitmap(100, 100, PixelFormat.Format32bppArgb)
use gra = Graphics.FromImage(bmp)
let sizeOf (opt: RenderOptions) s =
use sFormat = new StringFormat(StringFormat.GenericTypographic)
let font = if opt.IsSuper then opt.SmallFont else opt.NormalFont
let size = gra.MeasureString(s, font, PointF(0.0f, 0.0f), sFormat)
let height = int size.Height
{
Width = int size.Width + 2
Height = height
Midline = height/2
}
let precPow = 70
let precProd1, precProd2 = 30, 40
let precAdd1, precAdd2 = 10, 11
let precStart = 5
let precNeg1, precNeg2 = 1, 20
let sym opt s = Symbol (s, sizeOf opt s)
let applyPrec opt pprec prec exprs (size: ExprSize) =
if pprec > prec then
sym opt "(" :: exprs @ [sym opt ")"],
size.Expand [sym opt "("; sym opt ")"]
else
exprs, size
let mkSequence opt pprec prec exprs =
let size = ExprSize.Seq exprs
let exprs, size = applyPrec opt pprec prec exprs size
Sequence (exprs, size)
let rec expFunc opt f par =
let f' = sym opt f
let exprs' = [sym opt "("; exp opt precStart par; sym opt ")"]
Sequence (f' :: exprs', f'.Size.Expand exprs')
and exp (opt: RenderOptions) prec = function
| Num n ->
let s = n.ToString() in Symbol (s, sizeOf opt s)
| Var v ->
Symbol (v, sizeOf opt v)
| Neg e ->
let e' = exp opt precNeg1 e
let exprs, size = applyPrec opt prec precNeg1 [e'] e'.Size
let exprs' = [sym opt "-"] @ exprs
mkSequence opt prec precNeg2 exprs'
| Add exprs ->
let exprs' =
[ for i,e in Seq.mapi (fun i x -> (i,x)) exprs do
let first = (i=0)
let e' = exp opt (if first then precAdd1 else precAdd2) e
if first || e.IsNegative
then yield! [e']
else yield! [sym opt "+"; e'] ]
mkSequence opt prec precAdd1 exprs'
| Sub (e1, exprs) ->
let e1' = exp opt prec e1
let exprs' =
[ for e in exprs do
if e.IsNegative then
let e' = exp opt precAdd2 e.Negate
yield! [sym opt "+"; e']
else
let e' = exp opt precAdd2 e
yield! [sym opt "-"; e'] ]
mkSequence opt prec precAdd1 (e1'::exprs')
| Prod (e1, e2) ->
let e1' = exp opt precProd1 e1
let e2' = exp opt precProd2 e2
let exprs' =
if Expr.StarNeeded e1 e2
then [e1'; sym opt "*"; e2']
else [e1'; e2']
mkSequence opt prec precProd1 exprs'
| Pow (e1, e2) ->
let e1' = exp opt precPow e1
let e2' = exp { opt with IsSuper=true } precPow (Num e2)
Power (e1', e2', e1'.Size.AddPower e2')
| Sin e ->
expFunc opt "sin" e
| Cos e ->
expFunc opt "cos" e
| Exp expo ->
let e' = sym opt "e"
let expo' = exp { opt with IsSuper=true } precPow expo
Power (e', expo', e'.Size.AddPower expo')
| Frac (e1, e2) ->
let e1' = exp opt precStart e1
let e2' = exp opt precStart e2
Fraction (e1', e2', e1'.Size.Frac e2'.Size opt)
let exp = exp opt precStart e
{ Expression=exp; RenderOptions=opt; }
The conversion implemented in Listing 12-14 is relatively straightforward. It uses various local helper functions to break each expression into smaller visual elements, carefully keeping track of the bounding-box calculation. There are a number of things to consider: precedence is enforced, and expressions are parenthesized as necessary. For example, consider how you convert a product:
| Prod (e1, e2) ->
let e1' = exp opt precProd1 e1
let e2' = exp opt precProd2 e2
let exprs' =
if Expr.StarNeeded e1 e2
then [e1'; sym opt "*"; e2']
else [e1'; e2']
mkSequence opt prec precProd1 exprs'
This code converts the two interior expressions and decides on a list of display symbols by first checking whether a multiplication symbol is required. The function mkSequence then calculates the size of this new list of expressions, applies precedence rules to determine whether parentheses are required, and produces a final visual element as a result.
Other cases are handled similarly; for sums, you iterate through the elements exprs in the sum using sequence expression notation. If you find a negative term, you omit the plus sign (so 1+(-2) is rendered as 1-2). Differences are treated similarly, but here you change negative terms to positive, so 3-2-(-1) becomes 3-2+1. When converting products, you omit the multiplication operator if you can.
Rendering
Listing 12-15 shows the code for rendering visual expressions. You may have noticed in the definition of the VisualElement type that the only directly drawable visual element is Symbol. The other constructors carry one or more visual elements that must be drawn recursively and according to a well-defined logic. The key observation in the rendering function in Listing 12-15 is that, when drawing each element, you pass in the x and y coordinates of the bounding box in which it’s to be drawn. You also pass in the size of the parent box in which the element is to be aligned (as guided by the midline property).
Listing 12-15. VisualExpr.fs (continued): Rendering Visual Expressions
type VisualExpr =
...
member self.Render =
let pt x y = PointF(float32 x, float32 y)
let rec draw (gra: Graphics) opt x y psize = function
| Symbol (s, size) ->
let font =
if opt.IsSuper then opt.SmallFont else opt.NormalFont
let x', y' = size.CenterOnMidline psize x y
gra.DrawString(s, font, opt.Brush, pt x' y')
| Power (e1, e2, size) ->
let x', y' = size.CenterOnMidline psize x y
draw gra opt x' (y'+e2.Height) e1.Size e1
draw gra { opt with IsSuper=true } (x'+e1.Width) y' e2.Size e2
| Sequence (exps, size) ->
let x', y' = size.CenterOnMidline psize x y
List.fold (fun (x, y) (e: VisualElement) ->
let psize' =
{
Width = e.Width
Height = psize.Height;
Midline =size.Midline
}
draw gra opt x y psize' e
x+e.Width, y) (x', y') exps |> ignore
| Fraction (e1, e2, size) as e ->
let psize1 =
{ psize with Height=e1.Height; Midline=e1.Midline }
let psize2 =
{ psize with Height=e2.Height; Midline=e2.Midline }
draw gra opt x y psize1 e1
gra.DrawLine(self.RenderOptions.Pen, x, y+size.Midline,
x+psize.Width, y+size.Midline);
draw gra opt x (y+e1.Height+size.FracSepHeight opt) psize2 e2
let bmp = new Bitmap(self.Expression.Width, self.Expression.Height,
PixelFormat.Format32bppArgb)
let gra = Graphics.FromImage(bmp)
gra.FillRectangle(new SolidBrush(Color.White), 0, 0,
self.Expression.Width+1, self.Expression.Height+1)
draw gra self.RenderOptions 0 0 self.Expression.Size self.Expression
bmp
Building the User Interface
Listing 12-16 is the final piece: the UI client (Main.fs). It’s simple yet powerful. The main form contains an input field and a preview panel where the expressions are rendered on the fly as typed in. When the user presses the Enter key, a new MDI child window is created, and the original, simplified, derived, and final expressions are rendered on it. A bit of extra work is involved in creating the child windows to make them scrollable.
Listing 12-16. Main.fs: The User Interface Client for the Visual Symbolic Differentiation Application
module Symbolic.Expressions.UI
open Symbolic.Expressions
open Symbolic.Expressions.Visual
open System.Windows.Forms
open System.Drawing
let CreateScrollableChildWindow parent =
let scroll = new ScrollableControl(Dock=DockStyle.Fill, AutoScroll=true)
let form2 = new Form(MdiParent=parent, BackColor=Color.White)
form2.Controls.Add scroll
form2, scroll
let NewExpression parent s es =
let form, scroll = CreateScrollableChildWindow parent
let AddLabel (top, maxw) (parent: Control) s =
let l = new Label(Text=s, AutoSize=true, Top=top)
parent.Controls.Add l
(top+l.Height), max maxw l.Width
let AddPic (top, maxw) (parent: Control) (e: Expr) =
let e' = VisualExpr.OfExpr RenderOptions.Default e
let bmp = e'.Render
let pic = new PictureBox(Image=bmp, Height=bmp.Height,
Width=bmp.Width, Top=top)
parent.Controls.Add pic
(top+bmp.Height), max maxw bmp.Width
let height, width = List.fold (fun top (lab, e) ->
AddPic (AddLabel top scroll lab) scroll e) (0, 0) es
form.Text <- s
form.Height <- min 640 (height+40)
form.Width <- min 480 (width+40)
form.Show()
let UpdatePreview (scroll: Control) e =
let e' = VisualExpr.OfExpr RenderOptions.Default e
let bmp = e'.Render
let pic = new PictureBox(Image=bmp, Height=bmp.Height, Width=bmp.Width)
scroll.Controls.Clear()
scroll.Controls.Add pic
let NewExpressionError form s =
let cform, scroll = CreateScrollableChildWindow form
let label = new Label(Text=s, Font=new Font("Courier New", 10.f), AutoSize=true)
scroll.Controls.Add label
cform.Show()
exception SyntaxError
let Parse s =
let lex = Lexing.LexBuffer<char>.FromString s
try ExprParser.expr ExprLexer.main lex
with _ -> raise SyntaxError
let NewStringExpression form s =
try
let e1 = Parse s
let e2 = Utils.Simplify e1
let e3 = Utils.Differentiate "x" e2
let e4 = Utils.Simplify e3
NewExpression form s ["Original:", e1; "Simplified:", e2;
"Derivative:", e3; "Simplified:", e4]
with
| SyntaxError ->
let msg = Printf.sprintf "Syntax error in:
%s" s
NewExpressionError form msg
| Failure msg ->
NewExpressionError form msg
let ConstructMainForm () =
let form = new Form(Text="Symbolic Differentiation Example",
IsMdiContainer=true,
Visible=true, Height=600, Width=700)
let label = new Label(Text="Enter function=", Width=100, Height=20)
let tb = new TextBox(Width=150, Left=100)
let panel = new Panel(Dock=DockStyle.Top, Height=tb.Height+50)
let preview = new Panel(Dock=DockStyle.Bottom, BackColor=Color.White,
Height=50, BorderStyle=BorderStyle.FixedSingle)
panel.Controls.AddRange([|label; preview; tb |])
form.Controls.Add(panel)
tb.KeyUp.Add (fun arg ->
if arg.KeyCode = Keys.Enter then
NewStringExpression form tb.Text
tb.Text <- ""
tb.Focus() |> ignore
else
try
let e = Parse tb.Text
UpdatePreview preview e
with
| _ -> ())
form
let form = ConstructMainForm ()
NewStringExpression form "cos(sin(1/(x^2+1)))"
Application.Run(form)
To recap, in this example you’ve seen the following:
- Two abstract syntax representations for different classes of algebraic expressions: one simple, and one much more realistic
- How to implement simplification and symbolic differentiation routines on these representations of algebraic expressions
- How to implement parsing and lexing for concrete representations of algebraic expressions
- How to perform size estimation and visual layout for abstract syntax representations of algebraic expressions, here using Windows Forms
- How to put this together into a final application
Summary
This chapter looked at two applications of language-oriented symbolic programming. The first was hardware modeling and verification using propositional logic and binary decision diagrams, where you saw how to use symbolic techniques to describe circuits as propositional logic formulae and then used brute-force and/or binary decision diagram techniques to analyze these for correctness. The second was algebraic symbolic differentiation and visualization, where you learned how to differentiate, simplify, and display algebraic expressions. These examples are only two of many in the large domain of symbolic computation problems, a domain where functional programming and F# truly excels.