9
ELLIPTIC CURVE CRYPTOGRAPHY
HAFIZUR RAHMAN AND SAIFUL AZAD
Contents
9.3.1 Adding Points in Elliptic Curves over ZP
9.4 Discrete Logarithm Problem
9.5 Elliptic Curve Cryptography
9.5.1 Elliptic Curve Diffie–Hellman Key Exchange
9.5.3 Elliptic Curve Encryption/Decryption
9.5.4 Encryption/Decryption Example
Keywords
Asymmetric key algorithm
Diffie–Hellman key exchange
Elliptic curve cryptography
Private key
Public key
9.1 Introduction
Although the RSA algorithm resolves the problem of a secret key, it experiences higher computational cost because of utilizing a longer key size, so that it becomes computationally infeasible to solve. On the other hand, elliptic curve cryptography (ECC) is another approach of an asymmetric algorithm that utilizes a smaller key size, but still ensures the same level of security. ECC is based on the elliptic curve discrete log problem, which is much harder to solve over factoring integers of the RSA algorithm. Since it is harder, even a smaller key is computationally infeasible to solve. According to National Institute of Standards and Technology (NIST) guidelines for public key sizes for the Advanced Encryption Standard (AES), an ECC key size of 163 bits can ensure comparable performance of 1024 bits of key size of the RSA algorithm, which is around six times higher than that of the ECC key size [1]. The ratio is even bigger for a higher number of bits.
The elliptic curve system was first introduced to the cryptographic arena by Neal Koblitz and Victor Miller, who worked at IBM [1]. Generally, parties involved in the secure message exchange must generate a private key and a public key by utilizing the points of an elliptic curve and by following an algorithm. A private key is kept secret, whereas a public key is publicized to the external world. Like the RSA algorithm, the confidentiality of a message is ensured by encrypting a message using the public key of the receiver, which can only be decrypted by using the relative private key. A message can also be digitally signed by encrypting it using the private key of the sender. It can be decrypted by anyone who holds the public key of the sender. For understanding the ECC algorithm, Section 9.2 describes the details of an elliptic curve for a real number (R) as well as for a finite field (ZR), and all the operations involved in encryption and decryption.
9.2 Elliptic Curves over R
An elliptic curve over the real numbers is the set of points (x, y) that satisfy the following equation:
y2 = x3 + ax + b |
(9.1) |
where x, y, a, and b are all real numbers. Equation (9.1) is said to be cubic or degree 3 since the highest exponent that exists in this equation is 3. Elliptic curves in the form of Equation (9.1) can be divided into two groups: singular and nonsingular [2]. In ECC, nonsingular curves are preferred so that a curve can be free from cusps or self-intersections. An elliptic curve is said to be nonsingular when it satisfies the following condition:
| 4a3 + 27b2 ≠ 0 | (9.2) |
An elliptic curve generated using Equation (9.1) is illustrated in Figure 9.1.
Although an elliptic curve over the real numbers is a good approach to understand the properties of an elliptic curve, it requires higher computational time to perform various operations and is sometimes inaccurate due to the rounding errors. However, cryptographic schemes require fast and precise arithmetic. Consequently, two types of elliptic curves are utilized in cryptographic applications:
Prime curves over a ZP, where p is a prime number and p > 3. All the variables and the coefficients are taken from a set of integers from 0 to p – 1, and calculations are performed over modulo p.
Binary curve over Galois field (2m), also known as GF(2m), where all the variables and coefficients are taken on the values in GF(2n) and calculations are performed over GF(2n).
Since prime curves do not have any extended bit fiddling operation [3] analogous to the binary curve, they are suitable for software implementations. Consequently, prime curve-based ECC is explained in this chapter with its pseudocodes, examples, and implementations.
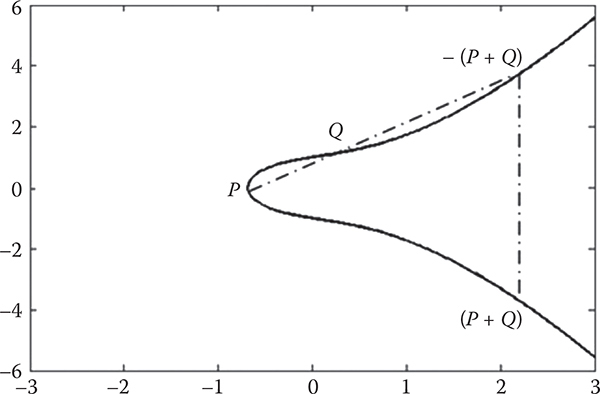
Figure 9.1 An example of an elliptic curve where a = b = 1.
9.3 Elliptic Curves over ZP
An elliptic curve over finite field ZP includes all points (x, y) in the ZP × ZP matrix that satisfies the following elliptic curve equation:
| y2 ≡ x3 + ax + b mod p | (9.3) |
where x and y are numbers in ZP, and similar to the real case, a and b must satisfy the following condition to form a finite abelian group [3]:
4a3 + 27b2 ≢ 0 mod p |
(9.4) |
Just to clarify here, in abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order (the axiom of commutativity).
Now, Equation (9.3) can be written as
y2 mod p = (x3 + ax + b) mod p |
(9.5) |
By replacing x, y, a, b, and p with the values 5, 1, 1, 0, and 23, we get
52 mod 23 |
= |
(13 + 1 × 1 + 0) mod 23 |
25 mod 23 |
= |
2 mod 23 |
2 |
= |
2 |
Hence, (1, 5) is a point on the curve over Z23. A similar procedure can be followed to find all the points of the curve. An algorithm for generating all the points of a prime curve is given below:
Algorithm 9.1: Calculate Points (PrimeNumber)
Begin
a ← 1
b ← 0
for x ← 0 to PrimeNumber
for y ← 0 to PrimeNumber
k ← y * y
m ← (x * x * x) + a * x + b
if (k% PrimeNumber = m% PrimeNumber)
store point (x, y) in a
container
end if
end for
end for
End
Using Algorithm 9.1, for a = 1, b = 0, and p = 23, the following points can be found:
X |
0 |
1 |
1 |
9 |
9 |
11 |
11 |
13 |
13 |
15 |
15 |
16 |
16 |
17 |
17 |
18 |
18 |
19 |
19 |
20 |
20 |
21 |
21 |
y |
0 |
5 |
18 |
5 |
18 |
10 |
13 |
5 |
18 |
3 |
20 |
8 |
15 |
10 |
13 |
10 |
13 |
1 |
22 |
4 |
19 |
6 |
17 |
Figure 9.2 plots all the points of the above-mentioned curve. As can be observed from the figure, the points do not form an elliptic curve; rather, they form a cloud of points in a finite field. This group also has another point that is known as the point at infinity, denoted as O, which is the identity element under an addition operation over points discussed in the next section. The negative of the point at infinity can be defined as –O = O, and the negative of any other point P = (xP, yP) on elliptic curve E to be its reflection over the x-axis, i.e., –P = (xP,–yP mod p).
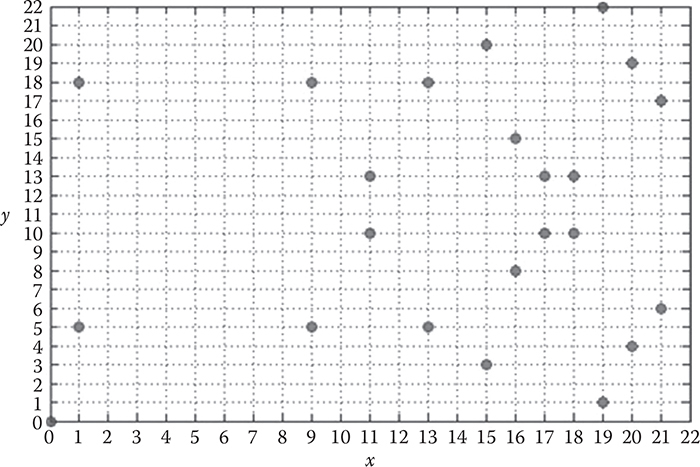
Figure 9.2 The elliptic curve for a = 1, b = 0, and P = 23.
Various arithmetic operations over points that are necessary to understand the ECC algorithm in detail are discussed below with relevant examples.
9.3.1 Adding Points in Elliptic Curves over ZP
Addition operations on an elliptic curve can be divided into three cases:
Adding two distinct points P and Q, when P ≠ Q: If P =(xP, yP)and Q =(xQ, yQ), then R = P + Q can be determined utilizing the following rules:
xR ≡ (S2 − xP − xQ) mod p, and
(9.6)
yR ≡ −yP + S(xP − xR) mod p
(9.7)
where S ≡ (yP − yQ) (xP − xQ)−1 mod p. Let us assume that P = (1, 5) and Q = (9, 18) are the points of Figure 9.2 we would like to add. Then,
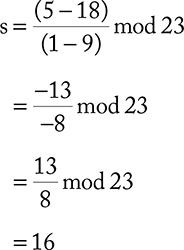
Now, utilizing the value of s, we can have xR and yR as follows:
xR
=
(162 − 1 − 9)mod 23
=
246 mod 23
=
16
yR
=
(−5 + 16(1−16))mod 23
=
−245 mod 23
=
8
Hence, R = (16, 8). The necessary algorithms to understand the addition of two distinct points over an elliptic curve are given below. In this process, Algorithm 9.2 demonstrates how the greatest common divisor (GCD) of two numbers can be found.
Algorithm 9.2: EGCD(a, b, & u, & v))//
Extended GCD Gives g = a*u + b*v
Begin
u ← 1, v ← 0, g ← a, u1 ← 0, v1 ← 1, g1 = b
while (g1 ! = 0)
q ←floor(g/g1)
t1 ← u - q*u1;
t2 ← v - q*v1;
t3 ← g - q*g1;
u ← u1
v ← v1
g ← g1
u1 ← t1
v1 ← t2
g1 ← t3;
end while
return g
End
Steps for calculating the inverse modulus are given in Algorithm 9.3.
Algorithm 9.3: InverseModulus(a, n)//Solve Linear Congruence Equation x*z = = 1 (mod n) for z
Begin
Local Variable: u, v, g, x
x ← x% n
g EGCD(x, n, u, v)//describe in Algorithm 2
if (g ! = 1)
z ← 0
else
z ← u% n
end if
return z
End
Algorithm 9.4 demonstrates how to perform negative modulus operations.
Algorithm 9.4: NegativeModulus(a, p)
Begin
b ← a * -1;
n ← ceiling((float)b/p)
return (n * p) - b
End
Algorithm 9.5 illustrates the steps to add two distinct points over an elliptic curve.
Algorithm 9.5: AddPoints(xp, yp, xq, yq, & xr, & yr, p)
Begin
n ← yp - yq
d ← xp - xq
if (d < 0)
n * = -1;
d * = -1;
end if
x ←; InverseModulus(d, p)//describe in Algorithm 3
if (n * x > 0) s = (n * x)% p;
elses = NegativeModulus(n * x, p)//describe in
Algorithm 4
end if
xr_ ←; (s * s - xp - xq)
if (xr_ < 0) xr NegativeModulus(xr_, p)
else xr ←; xr_% p
end if
yr_ ←; (-yp + s * (xp - xr));
if (yr_ < 0)yr ← NegativeModulus(yr_, p);
else yr = yr_% p;
End
Adding the points P and –P: The addition of the points P and –P poses a unique situation since the line through the two points is vertical, which will never intersect the elliptic curve at any point. So, it can be defined as P + (–P)= O, the point of infinity.
Adding a point with the point at infinity: When a point is added to the point of infinity, it produces the same point, e.g., P + O = P.
9.3.2 Scalar Multiplication
Scalar multiplication of k × P is a repetitive addition of a point P = (xP, yP), until it reaches k, where k > 0. For instance, when k = 3, in that case, 3P = P + P + P. If yP ≡ 0 mod p, then P =–P. In other cases, 2P = P + P = R,
xR ≡ s2 − 2xP mod p, and |
(9.8) |
yR ≡ −yP + s(xP − xR) mod p |
(9.9) |
where ![]() mod p. Let us assume that P = (11,10), then 2P can be calculated as
mod p. Let us assume that P = (11,10), then 2P can be calculated as
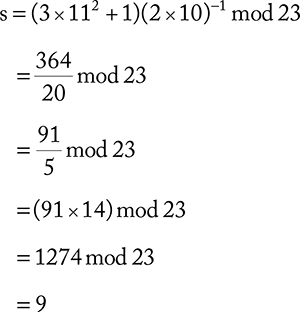
Now, utilizing the value of s, we can have xR and yR as follows:
xR |
= |
(92 − 2 × 11) mod 23 |
|
= |
(81 − 22) mod 23 |
|
= |
59 mod 23 |
|
= |
13 |
yR |
= |
−10 + 9 (11 − 13) mod 23 |
|
= |
(−10 − 18) mod 23 |
|
= |
−28 mod 23 |
|
= |
18 |
Hence, R = 2P = (13, 18). One important point to notice here is that 2P is now a distinctive point. Consequently, R + R =2R = 4P. To find 3P, we have to utilize Algorithm 9.5 since 2P and P are now two distinct points. Therefore, the x- and y-coordinates of 3P can be found using Equations (9.6) and (9.7). Similar procedures can be repeated to get the scalar multiplication of any k × P, where k > 0. Algorithms 9.6 and 9.7 illustrate the steps that can be followed to find the double of a point and a scalar multiplication of a point, respectively.
Algorithm 9.6: AddDouble(xp, yp, & xr, & yr, a, p)
Begin
n ← 3 * xp * xp + a
d ← 2 * yp
if (d < 0)
n ← n * -1;
d ← d * -1;
end if
x ← InverseModulus(d, p)//describe in
Algorithm 3
if (n * x > 0) s = (n * x)% p;
elses = NegativeModulus(n * x, p)//describe in
Algorithm 4
end if
xr_ ← (s * s -2 * xp)
if (xr_ < 0) xr ← NegativeModulus(xr_, p)
else xr ← xr_% p
end if
yr_ ← (-yp + s * (xp - xr));
if (yr_ < 0)yr NegativeModulus(yr_, p);
else yr = yr_% p;
End
Algorithm 9.7 demonstrates the scalar multiplication of a point to k times.
Algorithm 9.7: Scalar Multiplication (k, xp, yp, & xr, & yr)
Begin
add_double(xp, yp, xr, yr, a, p)
for i ← 0 to i < k - 2
xq ← xr;
yq ← yr;
xr ← 0
yr ← 0
add_points(xp, yp, xq, yq, xr, yr, p)
end for
End
9.4 Discrete Logarithm Problem
Let us consider the scalar multiplication of k × P = R, where P is a point of an elliptic curve and k < p. According to the rules of an abelian group [4], R is also going to be a point of that elliptic curve. It is relatively easy to calculate R when both k and P are known. However, it is relatively hard to discover k when R and P are known. This is known as the discrete logarithm problem for an elliptic curve. Let us assume that R = (16, 8) when P = (11, 10), and we would like to search out k utilizing the brute-force method.
P |
= |
(11, 10) |
2P |
= |
(13, 18) |
3P |
= |
(15, 20) |
4P |
= |
(9, 18) |
5P |
= |
(19, 22) |
6P |
= |
(1, 5) |
7P |
= |
(17, 10) |
8P |
= |
(18, 13) |
9P |
= |
(20, 19) |
10P |
= |
(16, 8) |
Since 10P = (16, 8) = R, therefore the discrete logarithm in this instance is k = 10. In real applications, a large value is chosen as k to make the brute-force attack infeasible.
9.5 Elliptic Curve Cryptography
In the following sections, we detail the ECC techniques by separating them into three subsections according to their functionalities.
9.5.1 Elliptic Curve Diffie–Hellman Key Exchange
Let us assume that A and B are two parties who desire to perform a secure message exchange. The first requirement to complete this process is to generate keys that can be done utilizing the steps mentioned below:
Both parties must agree upon a large prime number p and two elliptic curve parameters a and b of Equation (9.3), which defines the elliptic group of points EP(a, b).
Then, they have to pick a base point P on the elliptic curve EP(a, b) over a finite field ZP.
It is also necessary to choose a large integer number between 1 and the order of the abelian group EP(a, b), which would be considered a private key. Let us consider that A chooses m as its private key (PR A), and B chooses n as its private key (PRB).
A then generates a public key PUA = m × P.
B similarly generates a public key PUB = n × P.
After generating their relevant keys, they must exchange their public keys between each other. When A has the public key of B, it can now generate the secret key K = m × PUB. On the other hand, B can also generate the secret key K = n × PUA.
If we keenly observe the two produced secret keys, we see that they are the same because
m × PUB = m × (n × P) = n × (m × P)= n × PUB
9.5.2 Key Exchange Example
Let us now assume that the base point P = (15, 3). A chooses its private key m = 7, and B chooses its private key n = 5. Now,
PUA = m × P = 7 × (15, 3) = (15, 20)
PUB = n × P = 5 × (15, 3) = (20, 19)
Then, secret key K can be found as
KA |
= |
m × PUB |
|
= |
7 × (20, 19) |
|
= |
(20, 4) |
KB |
= |
n × PUA |
|
= |
5 × (15, 20) |
|
= |
(20, 4) |
KA |
= |
KB = K |
9.5.3 Elliptic Curve Encryption/Decryption
There are a lot of methods available in the literature that propose various techniques of elliptic curve encryption and decryption. In this chapter, one of the simplest techniques is chosen for those operations for a better understanding of the ECC algorithm. Let us consider that A wants to send a message to B that is also a point on the elliptic curve, M =(xM, yM). A must perform the following operations to encrypt the message:
C = M + m × PUB
Then, A sends the pair (m × P, C) to B, where P is the base point. After receiving the encrypted message, B utilizes its secret key to decrypt the message as follows:
C + (−n) × (m × P) |
= |
C −n × (m × P) |
|
= |
M + m × PUB −n ×(m × P) |
|
= |
M + m × (n × P) −n ×(m × P) |
|
= |
M |
9.5.4 Encryption/Decryption Example
Let us assume that A wants to transmit a message to B that is encoded on the elliptic point M = (19, 1). Consider the previous key exchange example where A and B have selected their own private key and also have exchanged their public key between each other. Now, encryption of message M can be found as follows:
C |
= |
(19, 1) + 7 × (20, 19) |
|
= |
(19, 1) + (20, 19) |
|
= |
(16, 8) |
m × P |
= |
7 × (15, 3) |
|
= |
(15, 20) |
Then, A sends the ciphertext {(15, 20), (16, 8)}. When B receives this ciphertext, it decrypts the message as follows:
M |
= |
(16, 8) − 5 × (15, 20) |
|
= |
(16, 8) − (20, 4) |
|
= |
(16, 8) + (20, −4) |
|
= |
(19, 1) |
9.6 Implementation 1
#include <iostream>
#include <cmath>
#include <conio.h>
using namespace std;
void ec_points(int a, int b, int p)
{
cout << "Points of Elliptic Curve" << endl;
cout << "— — — — — — — — — — — — — — — — — — — — — —
— — — — — — -" << endl;
for (int x = 0; x < p; x++) {
for (int y = 0; y < p; y++) {
int k = y * y;
int m = (x * x * x) + a * x + b;
if (k% p = = m% p) {
cout << "(" << x << "," << y << ")" << endl;
}
}
}
}
static int EGCD(int a, int b, int& u, int &v)//
Extended GCD gives g = a*u + b*v
{
u = 1;
v = 0;
int g = a;
int u1 = 0;
int v1 = 1;
int g1 = b;
while (g1 ! = 0)
{
int q = g/g1;//Integer divide
int t1 = u - q*u1;
int t2 = v - q*v1;
int t3 = g - q*g1;
u = u1; v = v1; g = g1;
u1 = t1; v1 = t2; g1 = t3;
}
return g;
}
//exitit 2
static int InvMod(int x, int n)//Solve linear
congruence equation x * z = = 1 (mod n) for z
{
//n = Abs(n);
x = x% n;//% is the remainder function, 0 < = x%
n < |n|
int u,v,g,z;
g = EGCD(x, n, u,v);
if (g ! = 1)
{
//x and n have to be relative prime for there to
exist an x^-1 mod n
z = 0;
}
else
{
z = u% n;
}
return z;
}
int NegMod (int a, int p)
{
int b = a * -1;
int n = ceil((float)b/p);
return (n * p) - b;
}
void add_points (int xp, int yp, int xq, int yq, int
&xr, int &yr, int p)
{
int s;
int n = yp - yq;
int d = xp - xq;
if (d < 0) {
n * = -1;
d * = -1;
}
int x = InvMod(d, p);
if (n * x > 0) {
s = (n * x)% p;
}
else {
s = NegMod(n * x, p);
}
int xr_ = (s * s - xp - xq);
if (xr_ < 0)
xr = NegMod (xr_, p);
else
xr = xr_% p;
int yr_ = (-yp + s * (xp - xr));
if (yr_ < 0)
yr = NegMod(yr_, p);
else
yr = yr_% p;
}
void add_double (int xp, int yp, int &xr, int &yr, int
a, int p)
{
int s;
int n = 3 * xp * xp + a;
int d = 2 * yp;
if (d < 0) {
n * = -1;
d * = -1;
}
int x = InvMod(d, p);
if (n * x > 0) {
s = (n * x)% p;
}
else {
s = NegMod(n * x, p);
}
int xr_ = (s * s - 2 * xp);
if (xr_ < 0)
xr = NegMod (xr_, p);
else
xr = xr_% p;
int yr_ = (-yp + s * (xp - xr));
if (yr_ < 0)
yr = NegMod(yr_, p);
else
yr = yr_% p;
}
void scalar_multiplication (int xp, int yp, int k,
int a, int p, int &PUx, int &PUy)
{
if (k = = 2) {
add_double(xp, yp, PUx, PUy, a, p);
}
else if (k > 2) {
add_double(xp, yp, PUx, PUy, a, p);
for (int i = 0; i < k - 2; i++) {
int xq = PUx;
int yq = PUy;
PUx = PUy = 0;
add_points(xp, yp, xq, yq, PUx, PUy, p);
}
}
else {
cout << "Wrong key" << endl;
}
}
void key_generation (int Px, int Py, int k, int a,
int p, int &PUx, int &PUy)
{
scalar_multiplication(Px, Py, k, a, p, PUx, PUy);
return;
}
void encryption (int Mx, int My, int k, int a, int p,
int PUx, int PUy, int &Cx, int &Cy)
{
int xr, yr;
scalar_multiplication(PUx, PUy, k, a, p, xr, yr);
add_points(Mx, My, xr, yr, Cx, Cy, p);
}
void decryption (int Cx, int Cy, int k, int a, int p,
int x1, int y1, int &Mx, int &My)
{
int xr, yr;
scalar_multiplication(x1, y1, k, a, p, xr, yr);
add_points(Cx, Cy, xr, -yr, Mx, My, p);
}
int main()
{
int a, b, p;
cout << "put a prime number: ";
cin >> p;
bool check;
do {
check = false;
cout << "put a value for a: ";
cin >> a;
cout << "put a value for b: ";
cin >> b;
if (((4 * a * a * a + 27 * b * b)% p) = = 0) {
cout << "Your values do not satisfied the
condition" << endl;
cout << "Please put values again" << endl;
check = true;
}
} while (check);
cout << "— — — — — — — — — — — — — — — — — — — — — — —
— — — — — — " << endl;
ec_points(a, b, p);
int Px, Py, PUAx, PUAy, PUBx, PUBy, Mx, My, Cx, Cy, m, n;
cout << "— — — — — — — — — — — — — -" << endl;
cout << "Key " << endl;
cout << "— — — — — — — — — — — — — -" << endl;
cout << "Select a base point (x,y) from the curve: ";
cin >> Px >> Py;
cout << "Select a private key for Alice: ";
cin >> m;
key_generation(Px, Py, m, a, p, PUAx, PUAy);
cout << "Public key of Alice is (" << PUAx << "," <<
PUAy << ")" << endl;
cout << "Select a private key for Bob: ";
cin >> n;
key_generation(Px, Py, n, a, p, PUBx, PUBy);
cout << "Public key of Bob is (" << PUBx << "," <<
PUBy << ")" << endl;
cout << "— — — — — — — — — — — — — — — — — — — — — — —
— — — " << endl;
cout << "Encryption/Decryption" << endl;
cout << "— — — — — — — — — — — — — — — — — — — — — — —
— — — " << endl;
cout << "Select a Message point (x,y) from the curve
(for encryption): ";
cin >> Mx >> My;
encryption(Mx, My, m, a, p, PUBx, PUBy, Cx, Cy);
cout << "Cipher is (" << Cx << "," << Cy << ")" << endl;
int x1, y1;
scalar_multiplication(Px, Py, m, a, p, x1, y1);
cout << "Alice send message pair(("<< x1 << "," << y1
<< "),(" << Cx << "," << Cy << "))" << endl;
cout << "||— — — — — — — — — — — — — — — — — — — —
-||" << endl;
cout << "Bob receive the message and start decrypting"
<< endl;
decryption(Cx, Cy, n, a, p, x1, y1, Mx, My);
cout << "Decrypted message is (" << Mx << "," << My <<
")" << endl;
getch();
return 0;
}
9.7 Implementation 2
#include<cstdlib>
#include<iostream>
#include<vector>
#include <math.h>
//contains utility functions
#define PrimeNumber 23
using namespace std;
class utils
{
public:
static float frand()//renerate random float number
{
static float norm = 1.0f/(float)RAND_MAX;
return (float)rand()*norm;
}
static int irand(int min, int max)//renerate random
integer number
{
return min+(int)(frand()*(float)(max-min));
}
//exhibit 1
static int EGCD(int a, int b, int& u, int
&v)//Extended GCD gives g = a*u + b*v
{
u = 1;
v = 0;
int g = a;
int u1 = 0;
int v1 = 1;
int g1 = b;
while (g1 ! = 0)
{
int q = g/g1;//Integer divide
int t1 = u - q*u1;
int t2 = v - q*v1;
int t3 = g - q*g1;
u = u1; v = v1; g = g1;
u1 = t1; v1 = t2; g1 = t3;
}
return g;
}
//exitit 2
static int InvMod(int x, int n)//Solve linear
congruence equation x * z = = 1 (mod n) for z
{
//n = Abs(n);
x = x% n;//% is the remainder function, 0 < = x%
n < |n|
int u,v,g,z;
g = EGCD(x, n, u,v);
if (g ! = 1)
{
//x and n have to be relative prime for there to
exist an x^-1 mod n
z = 0;
}
else
{
z = u% n;
}
return z;
}
};
//Template parameter 'curveOrder' is the order of the
finite field over which this curve is defined
template<int curveOrder>
class EllipticCurve;
//Template parameter 'curveOrder' is the order of the
finite field over which this curve is defined
template<int curveOrder>
class Element
{
int value;
//set element value
void setValue(int i)
{
value = i;
if (i<0)
{
value = (i%curveOrder) +
2*curveOrder;//ensure that the
value is in the correct range
}
value% = curveOrder;
}
public:
//default constructor
Element()
{
value = 0;
}
//constructor with value
explicit Element(int i)
{
setValue(i);
}
//copy constructor
Element(const Element<curveOrder>& rhs)
{
value = rhs.value;
}
//access Element Value
int getValue() const {return value;}
//negate
Element<curveOrder> operator-() const
{
return Element<curveOrder>(-value);
}
//setValue from integer
Element<curveOrder>& operator = (int i)
{
setValue(i);
return *this;
}
//" = " operator overload
Element<curveOrder>& operator = (const
Element<curveOrder>& rhs)
{
value = rhs.value;
return *this;
}
//"* = " operator overload
Element<curveOrder>& operator* = (const
Element<curveOrder>& rhs)
{
value = (value*rhs.value)%curveOrder;
return *this;
}
//"* = " operator overload
friend bool operator = =(const
Element<curveOrder>& lhs, const
Element<curveOrder>& rhs)
{
return (lhs.value = = rhs.value);
}
//" = =" operator overload
friend bool operator = =(const
Element<curveOrder>& lhs, int rhs)
{
return (lhs.value = = rhs);
}
//"! = " operator overload
friend bool operator! = (const
Element<curveOrder>& lhs, int rhs)
{
return (lhs.value ! = rhs);
}
//"/" operator overload
friend Element<curveOrder> operator/
(const Element<curveOrder>& lhs, const
Element<curveOrder>& rhs)
{
return Element<curveOrder>(lhs.
value * utils::InvMod(rhs.
value,curveOrder));
}
//"+" operator overload
friend Element<curveOrder>
operator+(const Element<curveOrder>& lhs,
const Element<curveOrder>& rhs)
{
return Element<curveOrder>(lhs.
value + rhs.value);
}
//"+" operator overload
friend Element<curveOrder> operator+(int
i, const Element<curveOrder>& rhs)
{
return Element<curveOrder>(rhs.
value+i);
}
//"+" operator overload
friend Element<curveOrder> operator+(const
Element<curveOrder>& lhs, int i)
{
return Element<curveOrder>(lhs.
value+i);
}
//"-" operator overload
friend Element<curveOrder> operator-(const
Element<curveOrder>& lhs, const
Element<curveOrder>& rhs)
{
return Element<curveOrder>(lhs.
value - rhs.value);
}
//"-"(binary) operator overload
friend Element<curveOrder> operator*(int
n, const Element<curveOrder>& rhs)
{
return Element<curveOrder>(n*rhs.
value);
}
//"*"(binary) operator overload
friend Element<curveOrder> operator*(const
Element<curveOrder>& lhs, const
Element<curveOrder>& rhs)
{
return Element<curveOrder>(lhs.
value * rhs.value);
}
//output stream handler
template<int T>
friend ostream& operator<<(ostream& os,
const Element<T>& opt)
{
return os << opt.value;
}
};
//Template parameter 'curveOrder' is the order of the
finite field over which this curve is defined
template<int curveOrder>
class Point
{
//elliptic curve pointer in which this point
will belong
EllipticCurve<curveOrder> *ellipticCurve;
/*
Given a curve 'ec' defined along some
equation in a finite field (such as 'ec':
y^2 = x^3 + ax + b)
point multiplication is defined as the
repeated addition of a point along that
curve.
wiki link http://en.wikipedia.org/wiki/
Elliptic_curve_point_multiplication
point multiply
*/
Point scalarMultiply(int k, const Point& a)
{
Point acc = a;
Point res = Point(0,0,*ellipticCurve);
int i = 0, j = 0;
int b = k;
while(b)
{
if (b & 1)
{
addDouble(i-j,acc);//bit is
set; acc = 2^(i-j)*acc
res + = acc;
j = i; //last bit set
}
b >> = 1;
++i;
cout << res.getX() << " " << res.
getY() << endl;
}
return res;
}
//doubling step for point multiplication
void addDouble(int multiplier, Point& point)
{
if (multiplier > 0)
{
Point tempPoint = point;
for (int i = 0; i < multiplier; i++)
{
tempPoint + = tempPoint;//
repeated addition
}
point = tempPoint;
}
}
//adding two points on the curve
void addPoints(Element<curveOrder> x1,
Element<curveOrder> y1, Element<curveOrder> x2,
Element<curveOrder> y2, Element<curveOrder> &
xR, Element<curveOrder> & yR) const
{
//special cases involving the additive
identity
if (x1 = = 0 && y1 = = 0)
{
xR = x2;
yR = y2;
return;
}
if (x2 = = 0 && y2 = = 0)
{
xR = x1;
yR = y1;
return;
}
if (y1 = = -y2)
{
xR = yR = 0;
return;
}
//the additions
Element<curveOrder> s;
if (x1 = = x2 && y1 = = y2)
{
//2P
s = (3*(x1.getValue()*x1.
getValue()) + ellipticCurve-
>getA())/(2*y1);
xR = ((s*s) - 2*x1);
}
else
{
//P+Q
s = (y1 - y2)/(x1 - x2);
xR = ((s*s) - x1 - x2);
}
if (s ! = 0)
{
yR = (-y1 + s*(x1 - xR));
}
else
{
xR = yR = 0;
}
}
public:
Element<curveOrder> x;//x coordinate
Element<curveOrder> y;//y coordinate
//point constructor with x and y value
Point(int x, int y)
{
this->x = x;
this->y = y;
this->ellipticCurve = 0;
}
//point constructor with x value, y value and
EllipticCurve pointer
Point(int x, int y, EllipticCurve<curveOrder> &
EllipticCurve)
{
this->x = x;
this->y = y;
this->ellipticCurve = &EllipticCurve;
}
//point constructor with constant x pointer,
constant y pointer and EllipticCurve pointer
Point(const Element<curveOrder>& x, const
Element<curveOrder>& y,
EllipticCurve<curveOrder> & EllipticCurve)
{
this->x = x;
this->y = y;
this->ellipticCurve = &EllipticCurve;
}
//compy constructor
Point(const Point& rhs)
{
x = rhs.x;
y = rhs.y;
ellipticCurve = rhs.ellipticCurve;
}
//access x component as element
Element<curveOrder> getX() const {return x;}
//access y component as element
Element<curveOrder> getY() const {return y;}
//calculate the order of this point using brute-
force additions
unsigned int Order(unsigned int maxPeriod = ~0)
const
{
Point r = *this;
unsigned int n = 0;
while(r.x ! = 0 && r.y ! = 0)
{
++n;
r + = *this;
if (n > maxPeriod) break;
}
return n;
}
//negate
Point operator-()
{
return Point(x,-y);
}
//" = " operator overload
Point& operator = (const Point& rhs)
{
x = rhs.x;
y = rhs.y;
ellipticCurve = rhs.ellipticCurve;
return *this;
}
//" = =" operator overload
friend bool operator = =(const Point& lhs, const
Point& rhs)
{
return (lhs.ellipticCurve = = rhs.
ellipticCurve) && (lhs.x = = rhs.x) &&
(lhs.y = = rhs.y);
}
//"! = " operator overload
friend bool operator! = (const Point& lhs, const
Point& rhs)
{
return (lhs.ellipticCurve ! = rhs.
ellipticCurve) || (lhs.x ! = rhs.x) ||
(lhs.y ! = rhs.y);
}
//"+" operator overload
friend Point operator+(const Point& lhs, const
Point& rhs)
{
Element<curveOrder> xR, yR;
lhs.addPoints(lhs.x,lhs.y,rhs.x,rhs.
y,xR,yR);
return Point(xR,yR,*lhs.ellipticCurve);
}
//"*" operator overload
friend Point operator*(int k, const Point& rhs)
{
return Point(rhs).operator* = (k);
}
//"*" operator overload
Point& operator+ = (const Point& rhs)
{
addPoints(x,y,rhs.x,rhs.y,x,y);
return *this;
}
//"* = " operator overload
Point& operator* = (int k)
{
return (*this = scalarMultiply(k,*this));
}
//ostream handler: print this point
friend ostream& operator <<(ostream& os, const
Point& p)
{
return (os << "(" << p.x << ", " << p.y <<
")");
}
};
//Template parameter 'curveOrder' is the order of the
finite field over which this curve is defined
template<int curveOrder>
class EllipticCurve
{
vector<Point<curveOrder> > pointTable; //table
of points
Element<curveOrder> a; //paramter a of
the EC equation
Element<curveOrder> b; //parameter b of
the EC equation
bool tableFilled; //true if the table has
been calculated
public:
//constructor with a and b as parameters (such
as 'elliptic curve' : y^2 = x^3 + ax + b)
EllipticCurve(int a, int b)
{
this->a = a;
this->b = b;
this->tableFilled = false;
}
//Calculate *all* the points (group elements) for this
'elliptic curve'
void CalculatePoints()
{
//calculate points
for (int x = 0; x < curveOrder; x++) {
for (int y = 0; y < curveOrder; y++) {
int k = y * y;
int m = (x * x * x) + a.getValue() * x +
b.getValue();
if (k% curveOrder = = m% curveOrder)
pointTable.push_back(Point<curveOrder>(x,y,
*this));
}
}
tableFilled = true;//table fill successful
}
//access the point vector like an array
Point<curveOrder> operator[](int n)
{
if (!tableFilled)
{
CalculatePoints();
}
return pointTable[n];
}
//number of elements in this group
size_t Size() const {return pointTable.size();}
//the degree P of this EC
int Degree() const {return curveOrder;}
//the parameter a (as an element of Fp)
Element<curveOrder> getA() const {return a;}
//the parameter b (as an element of Fp)
Element<curveOrder> getB() const {return b;}
//ostream handler: print this curve in human readable
form
template<int cO>
friend ostream& operator <<(ostream& os, const
EllipticCurve<curveOrder>& EllipticCurve)
{
//y^2 mod P = x^3 + ax + b mod P
os << "y^2 mod " << cO << " = (x^3 + ";
if (EllipticCurve.a ! = 0)
{
os << EllipticCurve.a.getValue() <<
"x + ";
}
if (EllipticCurve.b ! = 0)
{
os << EllipticCurve.b.getValue() ;
}
os << noshowpos << ") mod " << cO;
return os;
}
//print all the elements of the curve
ostream& PrintTable(ostream &os, int columns = 4)
{
if (tableFilled)
{
int col = 0;
vector<Point<PrimeNumber>
>::iterator iter = pointTable.
begin();
for (; iter! = pointTable.end();
++iter)
{
os << "(" <<
(*iter).x.getValue() << ", "
<< (*iter).y.getValue()
<< ") ";
if (++col > columns)
{
os << " ";
col = 0;
}
}
}
else
{
os << "EllipticCurve, F_" <<
PrimeNumber;
}
return os;
}
};
int main(int argc, char *argv[])
{
//curve object
int A, B;
bool flag;
do {
flag = false;
cout << "Put the value for a (an integer number
between 0 to " << PrimeNumber - 1 << ": ";
cin >> A;
cout << "Put the value for b (an integer number
between 0 to " << PrimeNumber - 1 << ": ";
cin >> B;
cout << endl;
if (((4 * A * A * A) + (27 * B * B))%
PrimeNumber = = 0) {
flag = true;
cout << "WARNING: Enterned values failed to
pass the singularity test" << endl;
cout << "Put the values again " << endl <<
endl;
}
} while (flag);
EllipticCurve<PrimeNumber> curveObject(A,B);
cout << "Elliptic Curve cryptography example —
— — — — — — — — — — — — — — — — — ";
//print some information about the curve
//cout << "The curve object: " << curveObject <<
" ";
curveObject.CalculatePoints();//
cout << " points on the curve object ";
curveObject.PrintTable(cout,4);
cout << " = = = = = = = = = = = = = = = = = =
= = = = = = = = = = = = = = = = = = = = = = = =
= = = = = ";
//Elliptic curve message encryption scheme
//the base point on the curve is used to
generate keys
Point<PrimeNumber> G = curveObject[0];
//choose G ramdomly where G > {0,0} with
order > = 2
while((G.getY() = = 0 || G.getX() = = 0) ||
(G.Order()<2))
{
int n = (int)(utils::frand()*curveObject.
Size());
G = curveObject[n];
}
cout << "G = " << G << ", order(G) is " <<
G.Order() << " ";
//sender 'Alice'
int a = utils::irand(1,curveObject.
Degree()-1);//session integer a which is also
used to generate Alice's public key
Point<PrimeNumber> Pa = a*G; //public key of
alice
cout << "Alice: Private key = " << a << endl;
cout << " public key Pa = " << a << "*" << G <<
" = " << Pa << endl;
//receiver 'Bob'
int b = utils::irand(1,curveObject.
Degree()-1);//session integer b which is also
used to generate bob's public key
Point<PrimeNumber> Pb = b*G; //public key of bob
cout << "Bob: Private key = " << b << endl;
cout << " public key Pb = " << b << "*" << G <<
" = " << Pb << endl;
//Jane, the eavesdropper
int j = utils::irand(1,curveObject.
Degree()-1);;//session integer j which is also
used to generate jane's public key
Point<PrimeNumber> Pj = j*G;
cout << "Jane: Private key = " << j << endl;
cout << " public key Pj = " << j << "*" << G <<
" = " << Pj << endl<< endl<< endl;
//Alice encrypts her message to send to Bob
int msg1 = 50;
int msg2 = 64;
cout << "Plain text from Alice to Bob: (" <<
msg1 << ", " << msg2 << ")"<<endl<<endl;
//alice encrypt the message using Bob's key
Point<PrimeNumber> encryptionKey = a*Pb;//
encryption key alice to bob
Element<PrimeNumber>
encrypt1(msg1*encryptionKey.getX());//encrypt
first chunk of message by multiplying with
encryption key's x value
Element<PrimeNumber>
encrypt2(msg2*encryptionKey.getY());//encrypt
second chunk of message by multiplying with
encryption key's y value
//encrypted message is: Pa,c1,c2
cout << "Encrypted message from Alice to Bob =
{Pa,c1,c2} = {" << Pa << ", " << encrypt1 << ",
" << encrypt2 << "} ";
//Bob now decrypts Alice's message, using her
public key and his session integer "b" which was
also used to generate his public key
Point<PrimeNumber> decryptionKey = b*Pa;//bob's
decryption key for alice
Element<PrimeNumber> decryptMsg1 = encrypt1/
decryptionKey.getX();//encrypt first chunk of
message by dividing with decryption key's x
value
Element<PrimeNumber> decryptMsg2 = encrypt2/
decryptionKey.getY();//encrypt second chunk of
message by dividing with decryption key's y
value
cout << " Bob's decrypted message from Alice =
(" << decryptMsg1 << ", " << decryptMsg2 << ")"
<< endl;
//Jane intercepts the message and tries to
decrypt it using her key
encryptionKey = j*Pa;//jane's decryption key for
alice
decryptMsg1 = encrypt1/encryptionKey.getX();//
encrypt first chunk of message by dividing with
decryption key's x value
decryptMsg2 = encrypt2/encryptionKey.getY();//
encrypt second chunk of message by dividing with
decryption key's y value
cout << " Jane's decrypted message from Alice =
(" << decryptMsg1 << ", " << decryptMsg2 << ")"
<< endl;
cout << endl;
system("PAUSE");
return EXIT_SUCCESS;
}
References
1. Certicom. The Basics of ECC. Available at https://www.certicom.com/index.php/the-basics-of-ecc
2. A. O’Maley. Elliptic curves and elliptic curve cryptography. Mathematics Exchange, 3(1), 2005.
3. L. Jensen. Bit fiddling operations. Available at http://cs-linux.ubishops.ca/~jensen/asm/notes/note7.htm
4. W. Stallings. Cryptography and network security, 4th ed. Pearson Prentice Hall of India, New Delhi, 2006.
