Chapter 12: Fundamentals of Identity Based Cryptography

Cryptography, when applied to network security, describes the art of coding information into secrets that are transmitted over a public channel to an intended receiver. The latter is the only entity capable of recovering the initial information from the secrets. That is, any entity can get the encrypted information, i.e., the ciphertext. However, it will not be able to recover the original content of the message, namely, the plaintext, unless it gets the key that has been used for encryption. Cryptography has been used for a long time to provide security properties such as data confidentiality, data integrity, and data origin authentication.

Data confidentiality ensures that the ciphertext does not provide any information about the plaintext. Generally, the confidentiality property is provided by symmetric or asymmetric encryption. Integrity mechanisms serve to detect any modification of the transmitted data thanks to the use of hash functions in a signature or in a keyed-hash message authentication code (HMAC).

Cryptography not only serves to authenticate communicating entities thanks to the use of authentication protocols such as Transport Layer Security (TLS), but also serves to authenticate data origin thanks to the use of HMAC or signatures. Moreover, cryptography ensures nonrepudiation; namely, none of the communicating parties could deny its participation to the communication.

In this chapter, we review the concepts of symmetric cryptography and public-key cryptography in Section 12.1. We review the famous Diffie–Hellman and RSA algorithms. Then, we introduce elliptic curve cryptography (ECC) before describing ID-based cryptography (IBC) in Section 12.2.

12.1 Introduction to Cryptography

Cryptography is based on mathematical algorithms that use, in general, abstract algebra and groups theory. These algorithms need a secret input that is usually named a key. The encryption schemes are trapdoor functions that are easy to compute with the key. However, they are hard or almost impossible to invert without the key. Kerckhoffs [1] announced that “a cryptosystem should be secure even if everything about the system is public knowledge, except the key.” The same principle was reformulated by Shannon [2], as “the enemy knows the system.”

During the second part of the twentieth century, the field of cryptography expanded drastically thanks to the appearance of new cryptographic systems. In fact, Diffie and Hellman revolutionized cryptography in 1976 by defining the first asymmetric cryptosystem. Then, Shamir proposed the RSA algorithm with Rivest and Adleman, before publishing his outstanding works on threshold and ID-based cryptographies. Then in 1985, Koblitz and Miller presented the first elliptic curve-based cryptosystem. Finally, quantum cryptography appeared as the cryptography of the future, as it relies on optic and light theories, but not on groups and fields theory. In quantum cryptography, every bit is represented by the polarization of a photon.

In this section, we briefly describe the concepts of symmetric cryptography (Section 12.1.1). Then, in Section 12.1.2 we present public-key cryptography in depth.

12.1.1 Symmetric Cryptography

Symmetric cryptography is based on sharing a secret key between two communicating entities, Alice and Bob. Symmetric cryptography, as well as asymmetric cryptography, relies on the use of two related algorithms for message encryption and decryption. We denote the encryption algorithm by E and the decryption algorithm by D. The encryption algorithm takes as inputs the plaintext message m and a key k, and outputs the ciphertext c. Meanwhile, the decryption algorithm D takes as inputs c and k, and outputs m. Let K be the set of keys, M the set of messages, and C the set of ciphertexts; we define E and D as follows:

E:M × K → C	D:C × K → M
(m,k) → c	(c,k) → m

We say that an encryption algorithm is well defined if it verifies the equation

D (E (m, k), k) = m

The Vernam one-time pad [3] is one of the oldest symmetric encryption algorithms. It was patented in 1919. Vernam assumes that the message m, the key k, and the c ciphertext have the same bit lengths. The one-time pad relies on the exclusive-or (XOR) as encryption and decryption functions. Recall that XOR is equivalent to a binary sum modulo 2. When Alice wants to cipher a message m to Bob (Figure 12.1), Alice computes c = m ⊕ k. Bob deciphers the message using the same key m = c ⊕ k. Vernam’s encryption is called a onetime pad, as the key k is used once for ciphering a unique message m. Therefore, the key has to be renewed for every message.

Shannon proved that the Vernam algorithm provided perfect secrecy if the key length is at least equal to the message length. Perfect secrecy means that an eavesdropper, Eve, does not distinguish the encryption of a message m₀ from that of a message m₁. That is, no information is recovered about the plaintext from the ciphertext. In other words, Vernam’s algorithm verifies the following equation for every key k uniformly chosen in K:

Pr (m₀ ⊕ k = c) = Pr (m₁ ⊕ k = c), ∀ m₀, m₁ ∈ M/m₀ ≠ m₁

(12.1)

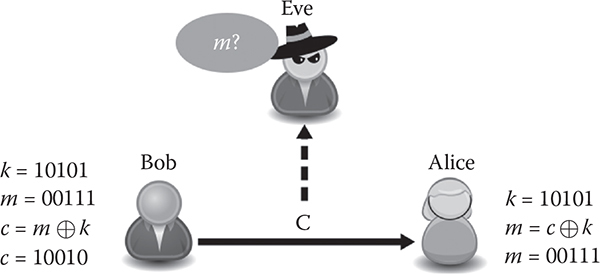
Figure 12.1 Vernam’s one-time pad.

In other words, Equation (12.1) implies that the ciphertexts are uniformly distributed in C. Vernam encryption has many drawbacks. We stated that the key has to be renewed for every message. As such, Alice and Bob have to provide a secure communication channel to exchange a new key for every transmitted message. This is not feasible in practice because Alice and Bob will be wasting half of their communication time in exchanging keys (supposing that they manage a secure channel, for example, by using quantum cryptography). In order to remove the problems of the one-time pad algorithm, new types of symmetric encryption algorithms appeared. They are called the block ciphers, as they cipher small blocks of data using small keys of 64, 128, or 256 bits length. These algorithms rely on permutation. The most famous ones are the Data Encryption Standard (DES) [4] and the Advanced Encryption Standard (AES) [5].

12.1.2 Asymmetric Cryptography

Public-key or asymmetric cryptography gives two entities the opportunity to exchange information over an in secure channel while providing data confidentiality, nonrepudiation, and authenticity. In addition, it permits two entities that have never met before to mutually authenticate themselves. Contrary to symmetric cryptography where two communicating entities have to share the same secret key, public-key cryptography relies on two keys to secure the exchanged information. The pair of keys is formed by a public key and a private key, which are related by a mathematical equation. Solving this mathematical equation comes to breaking a hard mathematical problem such as the discrete logarithm problem (DLP). Each entity shares its public key with its communicating peers. However, its private key must be kept secret (Figure 12.2).

In practice, a public-key infrastructure (PKI) is deployed and a certification authority (CA) is used to certify the mapping between an entity and its public key. The CA is a trusted third party that signs a certificate that contains the public key and the identification information of a user. In addition, the certificate provides information about its issuing CA and includes a unique serial number. The serial number serves to quickly identify the certificate during management operations. The CA should not know the private key, which corresponds to the public key included in the certificate. Examples of CAs include Verisign, Comodo, CAcert, and Thawte.

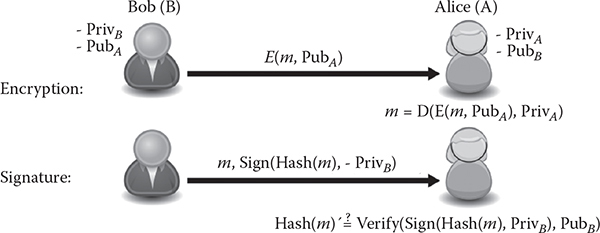
Figure 12.2 Public-key cryptography.

Many certification authorities can be overlapped in a hierarchical fashion. That is, the certificate of the parent CA serves to verify the certificates of its children CAs until reaching the root CA. The root CA self-signs its own certificate, and it has to be trusted. In practice, we define two types of CAs. The private CA is defined inside a private company or a university. It is easy to manage, as certificate usage is limited to a local area. In addition, the user’s identification is easy and can be done, for example, in a human resources service before issuing a certificate. Meanwhile, the public CA issues certificates to secure transactions over the Internet and to authenticate unknown parties. These certificates are used widely and are not limited to small domains. This type of CA requires more caution when authenticating the users.

The CA manages certificate revocation lists (CRLs) to indicate which certificates are revoked, and so the keys that become invalid. CRLs can be viewed as databases that are securely managed by the CA. In practice, the CA has two different manners of updating the CRLs. In the first case, the CA requests from the users to check periodically the CRL. As such, the users have to always be online to check the list of revoked certificates. In the second case, the CA distributes its CRL periodically to the users.

The two ways of CRL management increase the bandwidth consumption due to the number of CRL requests and responses, or due to the size of the transmitted CRL. Moreover, in the period separating two CRL updates, users do not know the newly revoked certificates, and consequently, attackers that successfully compromised a private key (also very recently revoked) can impersonate as a legitimate network user. For more details about PKI, interested readers are invited to consult the following books: [6], [7], and [8].

We next present the first public-key scheme: the Diffie and Hellman (DH) key exchange algorithm [9] (Section 12.1.3). Then, we review the Rivest, Shamir, and Adleman (RSA) algorithms [10] (Section 12.1.4). DH and RSA cryptosystems are based on the theory of multiplicative groups and on integer factorization into a product of primes, respectively. Finally, we describe the elliptic curve cryptography (ECC) [11] that relies on an additive group of points of an elliptic curve (Section 12.1.5).

12.1.3 Diffie–Hellman (DH) Algorithms

Diffie and Hellman [9] proposed in 1976 a mechanism to share a secret key between two parties, Alice (A) and Bob (B). The public elements provided to each party are the prime P and a generator g of . Alice and Bob generate their public elements K_A = g^a and K_B = g^b and from their secret private keys a and b, which are randomly selected in . The DH steps are the following:

• Alice → Bob: {ID_A, K_A}: Alice starts the key computation by sending to Bob her public key K_A with her identity ID_A. Upon receiving this message, Bob computes the shared key K_AB such that K_AB = (K_A)^b = (g^a)^b. Then, Bob responds to Alice with his own public key K_B = g^b.

• Bob → Alice: {ID_B, K_B}: Upon receiving this message, Alice computes the shared key K_AB = (g^b)^a.

The DH weakness is the man in the middle (MIM) attack. That is, Eve creates a shared secret with Alice and Bob by impersonating as Bob from one side and as Alice from the other side. However, the MIM attack can be easily removed by making Alice and Bob sign their chosen public elements.

The DH security is based on the definition of the following mathematical problems:

• The Diffie–Hellman problem (DHP) consists of recovering the secret key k = g^a.b mod[p] given the prime p, the generator g of , g^amod[p] and g^bmod[p].

• The discrete logarithm problem (DLP) consists of finding the secret value given the prime p, the generator g of , and the public value k such that k = g^a mod[p]. It is clear that the DHP is not harder than the DLP because any algorithm that solves the DLP solves the DHP too. Indeed, if Eve recovers a from g^a, she will be able to compute g^b.a using the captured g^b.

There are various methods for solving the DLP. The basic one is the exhaustive search, which consists of evaluating gⁱ for i = 0, 1, ..., p – 2 until finding the sought value. This method requires an average of O(p) multiplications. The exhaustive search is actually inefficient for long prime p. For example, if p is 160 bits long, the time needed for trying all the possibilities is around O(2¹⁶⁰). However, more efficient algorithms such as the baby-step giant-step algorithm and Pollard’s rho algorithm require steps. In addition, Pohlig–Hellman proposed an algorithm that solves the DLP in 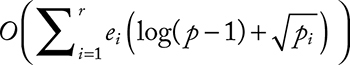where Pohlig–Hellman thought that the decomposition of p – 1 into a product of prime numbers would impact the DLP resolution time, as it consists of finding s from k = g^s mod[p] with ∈ . Nowadays, the index calculus is the most efficient method for solving the DLP in 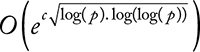. More details about DLP resolution can be found in Chapter 3 of the Handbook of Applied Cryptography [12].

12.1.4 Rivest, Shamir, and Adleman (RSA) Algorithms

Rivest, Shamir, and Adleman [10] presented the famous RSA schemes in 1978. RSA key generation, encryption, and signature are based on the difficulty of integer factorization into a product of prime numbers.

To generate an RSA key, we first choose two large and distinct random primes p and q and compute the integer n as n = p.q. Then, we compute the Euler function φ(n) = (p–1).(q–1). We select a random integer e such that 1 < e <φ (n), where e and φ(n) are co-prime (i.e., gcd (e, φ(n)) = 1). Finally, we compute the unique integer d such that 1 < d < φ(n) and e. d. = 1 mod[φ(n)]. Such an integer d can be found using the extended Euclidean algorithm ([13], Chapter 1). The public key is formed by the tuple (n, e) and its corresponding private key is the integer d.

We present, in the following, the RSA encryption and signature algorithms:

• RSA encryption and decryption: Let us suppose that Bob is going to encrypt a message to Alice. Bob transforms the message to an integer m in . Then, Bob computes c = m^e mod[n] and sends the ciphertext c to Alice. To recover the plaintext from the ciphertext, Alice executes the following operation:

c^dmod[n] = m^e.dmod[n] = m^{⁽¹⁺^k^.^φ⁽ⁿ⁾⁾} mod[n] = m mod[n]

Note that the decryption is based on the theorem of Euler, which states:

• RSA signature generation and verification: We suppose that Bob wants to sign the message m before sending it to Alice. Bob first computes the hash h = H(m) and transforms it to an integer in . Then, using its private key d, he computes s = h^dmod[n]. Finally, Bob sends s and m to Alice. Alice verifies the RSA signature with Bob’s public key (e, n). First, she computes h′ = H(m). Then, she recovers h = s^emod[n] = h^e,dmod[n]=h mod[n]. Finally, Alice compares h to h′. If the two hash values are equal, the signature is valid; otherwise, it is rejected.

The RSA security depends on the difficulty of factoring the number n into the product of two primes p and q. If the trivial trial and division method is used for the factoring, we divide n by i = 2, 3, 5, 7, 11, ... until hitting the smallest prime between p and q. That is, the running time for the trial and division algorithm will be around either o(p) if p < q or o(q) if q < p. However, a more efficient method, called quadratic sieve factoring, factors the integer n into a product of two primes in approximately 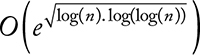. More details about sieving methods can be found in Chapter 3 of the Handbook of Applied Cryptography [12].

12.1.5 Elliptic Curve Cryptography (ECC)

Elliptic curves (ECs) are cubic forms that are defined over finite fields, generally a prime or a binary field denoted or , where p and 2 ^p represent the order of the field. By order, we mean the number of elements of the field. In this chapter, we only consider elliptic curves that are defined over finite prime fields. That is, all the calculus in the field is done mod[p].

An elliptic curve E() is defined by the following Weierstrass equation [14]:

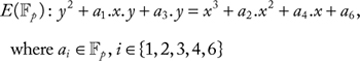
The points of E() form an additive abelian group. That is, the binary operation of the group is the addition of two points, and the identity element of the group is a special point, called the point at infinity P_∞.

The addition of EC points can be specified graphically as presented in Figure 12.3. Let P and Q be two distinct points belonging to E(); the sum S of P and Q is obtained by drawing a line through P and Q. This line intercepts E in a third point R.S is the reflection of R relative to the x-axis.

The double of the point P is obtained by drawing the tangent to E() in P. This tangent intercepts the curve in a point R. S, the symmetric of R relative to the x-axis, is equal to 2.P. When the tangent in P happens to be vertical, we say that 2.P = P_∞, where P_∞ is the identity element of the additive group. For simplicity, we imagine that the curve cuts the vertical tangent at infinity in the point P_∞.

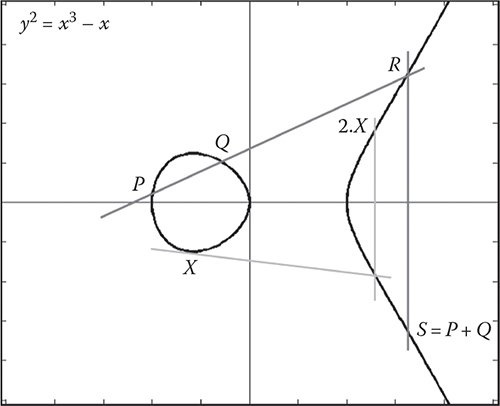
Figure 12.3 Elliptic curve points addition.

To compute the inverse –P of a point P = (x, y), we just take –P = (x, –y). As such, the vertical line passing through P and –P cuts the curve at P_∞. That is P + (–P) = P_∞.

The elliptic curve E() is said to be well defined (or smooth) if its discriminant Δ is different from 0. The condition Δ ≠ 0 ensures that the EC does not contain singular points for which the addition cannot be defined. The expression of the discriminant Δ is described by the following equalities:

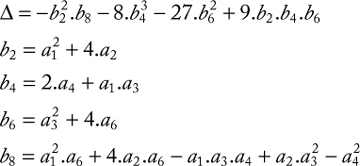
When the characteristic p of the field is greater than 2, the Weierstrass equation is simplified to become:

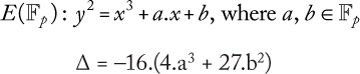
12.1.5.1 ECC Key Generation

Let us take G, a subgroup of E(), which is generated by the point P of prime order n. G contains the n following points: {P_∞, P, 2.P, 3. P, ..., (n–1).P}. Alice chooses a random integer as her private key and computes her corresponding public key as K_A = a. P. The problem of finding a given the primitive root P of G and the public key K_A denotes the Elliptic Curve Discrete Logarithm Problem (ECDLP). The ECDLP can be solved using the baby-step giant-step algorithm or Pollard’s rho algorithm in steps ([13], Chapter 5).

The DH protocol can be easily adapted to the elements of the additive group G. Alice and Bob have to just exchange their public elements K_A = a.P and K_B = b.P. Of course, Alice and Bob keep secret their respective private keys a and b. Then, they compute respectively their shared key as

K_AB = a.b.P = b.a.P = K_BA

Table 12.1 RSA and ECC Key Length Equivalences for the Same Security Levels

lk	80	112	128	192	256
RSA key length (bits)	1024	2048	3072	7680	15,360
ECC key length (bits)	160	224	256	384	512

In cryptography, the security level of a symmetric encryption algorithm is defined as the number of operations needed to break the algorithm when an l_k-bit key is used. For example, the number of elementary operations needed to break a block cipher encryption scheme is equal to 2^l^k [15]. The same result can be retrieved from Vernam’s one-time pad where c = m ⊕ k. The attacker has theoretically to try 2^l^k possibilities to find the good key k to recover m from c. Nowadays, l_k has to be at least equal to 80 bits. As such, the key research will take O(2⁸⁰) steps. Using a 4 GHz processor, we need around 9 million years to try all the possibilities, assuming that each possibility is computed during a clock cycle.

In asymmetric cryptography, the security level of an algorithm is set with respect to the hardness of the factoring integer (the case of RSA) or solving the ECDLP (the case of ECDSA). This concept of security level sets the length in bits of RSA and EC keys. Table 12.1 presents the equivalence between the lengths of RSA and EC keys, respectively, to the security level l_k, where l_k corresponds to the length in bits of a symmetric key k.

It is clear from Table 12.1 that it is more interesting to use EC keys than RSA keys when asymmetric cryptography is needed. For example, the current key size recommendation for legacy public schemes is 2048 bits. A vastly smaller 224-bit ECC key offers the same level of security. This advantage only increases with the security level. For example, a 3072-bit legacy key and 256-bit ECC key are equivalent, something that becomes important as stronger security systems become mandated and devices get smaller. ECC usage is expanding because elliptic curves require less storage, less power, less memory, and less bandwidth. They permit the implementation of cryptography in platforms that are constrained, such as wireless devices, handheld computers, and smart cards. They also provide a big gain in situations where efficiency is important.

12.1.5.2 Elliptic Curve Digital Signature Algorithm

We present, in this section, the ECDSA, which is the elliptic curve analog of the digital signature algorithm (DSA) [16]. Let us consider G, a subgroup of an elliptic curve E(), which is generated by the point P of prime order n.

To sign a message m, Bob chooses a random k in and computes the point k. P = (x, y). Then, he computes e = h(m) and s = k^–1(e+b.x) mod[n], where b is Bob’s private key. Finally, Bob sends m and its signature (x, s) to Alice.

At the reception (x, s) of and m, Alice computes e = h(m) and calculates the point X using the public key of Bob K_B = b. P as follows:

X = e.s^–1.P + x.s^–1.K_B = (x′, y′)

Then, Alice compares x′ to x. If the two values are equal, the signature is valid.

The signature verification holds because we have s = k^–1 (e + b.x) mod[n] which implies that k = s^–1 (e + b.x) mod[n]. Recall that the public key of Bob is K_B = b. P, we get

X = (x′, y′) = e.s^–1.P + x. s^–1. K_B = s^–1(e.P + x.b.P) = k.P = (x, y)

In the next section, we introduce IBC, which is a promising kind of asymmetric cryptography. In IBC, the public key of an entity is directly derived from its identity.

12.2 ID-Based Cryptography

IBC was initially introduced by Shamir [17] to provide entities with public and private key pairs with no need for certificates, CA and PKI. Shamir assumes that each entity uses one of its identifiers as its public key. These identifiers have to be unique. In addition, he assigns the private key generation function to a special entity called the private key generator (PKG). That is, before accessing the network, every entity has to contact the PKG to get back a smart card containing its private key. This private key is computed so as to be bound to the public key of the entity.

During the last decade, IBC has been improved by the integration of ECC [14]. As a consequence, new ID-based encryption and signature schemes emerged, and they differ from Shamir’s method in that the PKG does not rely on smart cards to store the private key and the ciphering information. In 2001, Boneh and Franklin [18] presented the first ID-based encryption scheme, where they used bilinear pairing functions to map elliptic curve points to a number in a multiplicative group.

Sometimes, certificates are considered as IBC, as they bind the user’s public key to his or her identity. In this chapter, IBC is considered as the cryptographic schemes where the public key is computationally derived from the identity. The public key is the output of a function (mostly a hash function) that takes as input the user’s identity.

There exist many types of IBC schemes. We focus, in this work, on the most commonly used schemes based on pairing functions [19]. For other schemes, we can state the work done by Cocks [20] for an ID-based encryption scheme using the computational difficulty of integer factorization and the quadratic residuosity problem.

In the following sections, we present the key generation processing for IBC. Furthermore, we introduce some well-known ID-based encryption (IBE) and signature (IBS) schemes that proved to be secure within the random oracle model [21]. The random oracle model serves to mathematically establish security proofs where cryptographic functions, like hash functions, are considered random abstract functions [22].

12.2.1 ID-Based Key Construction

When a station needs a private key, it provides the PKG with the identity ID intended to be used for its private-key computation. The PKG then derives the node’s private key using some domain parameters. For generating these parameters, the PKG runs a probabilistic polynomial time (PPT) algorithm that takes as input a security parameter

k and outputs the groups , and , and the pairing function ê from in and are additive groups of prime order q, and is a multiplicative group of the same order q. Note that the order q is defined with respect to k such that q > 2^k. Generally, and are subgroups of the group of points of an elliptic curve (EC) over a finite field and is a subgroup of a multiplicative group of a related finite field. The subgroup is generated by the point P while the subgroup is generated by the point. The point P (or the point Q) is used to compute another point P_pub = s.P (or Q_pub = s.Q), where s is the domain secret. The PKG chooses randomly the secret .

In addition to the definition of groups, some hash functions need to be defined in accordance to the IBE or IBS schemes that are going to be used. For example, a hash function H₁ that verifies is defined in order to transform the node’s identity into an EC point. Generally, the public key of a station is computed as a hash of one of its identities, and it is either a point of an elliptic curve or a positive integer. The list containing the groups and and , the bilinear mapping ê, the points P and P_pub and the hash functions form the domain public elements noted IBC-PEs. These IBC-PEs are distributed by the PKG to the network users because they are needed during the public-key derivation and the cryptographic operations.

The key derivation process starts when the PKG receives the ID of the node that is requesting a private key (Figure 12.4). First, the PKG computes the user’s public key as Pub_ID =Hash(ID). Then, the PKG generates the corresponding private key using the local secret value s. Note that the private key is computed as Priv_ID =f(s, Pub_ID). In practice, there are different ways for generating a private key from the public key. Here, we present the most known methods for private-key computation:

Basic key generation scheme: In the most common cases [18, 23, 24], we have Priv_ID=s.Pub_ID where is equal to H₁(ID), where .

Sakai-Kasahara key generation scheme: Sakai and Kasahara [25] proposed computing the private key as . P where Pub_ID =H₁(ID) and . As the public key is not an elliptic curve point but a scalar, the public-key computation is faster than hashing to an elliptic curve point.

Boneh and Boyen key generation scheme: Boneh and Boyen define three public points that are computed as P₁ =α.P, P₂ =β.P,

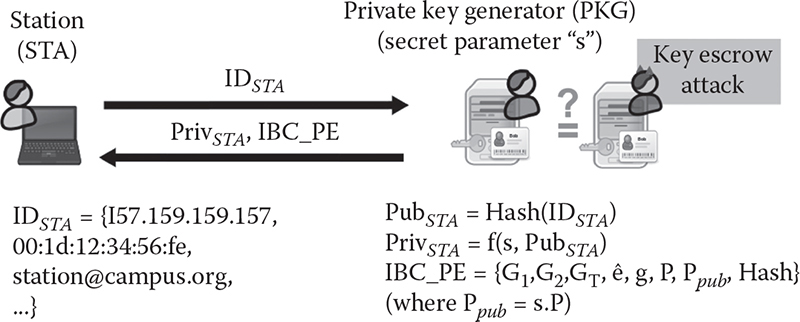
Figure 12.4 ID-based key generation.

and P₃ =ϒ.P where α, β, and ϒ are secrets selected by the PKG in . A node’s public key is computed as Pub_ID = H₁(ID) where . Meanwhile, the PKG computes the corresponding private key using the random r in as follows:

Priv_ID = (Priv₁, Priv₂) =(Pub_ID.r.P₁+α.P₂ +r.P₃, r.P)

That is, the private key is formed by two EC points.

After generating a private key, the PKG has to securely transmit it to its owner either by the use of cryptography or directly to the physical person (using a secure transportation device).

In all the aforementioned key derivation schemes, the PKG is generating the private key of stations (STAs) and, as such, is able to impersonate any of them by illegally generating signature or deciphering encrypted traffic. For mitigating that key escrow attack (KEA), a strong assumption is usually made necessary that the PKG is a trustworthy entity.

12.2.2 Pairing Functions

The pairing function ê has to be bilinear, nondegenerate, and efficiently computable. That is, the pairing function has to verify the following properties:

Bilinearity: The pairing function has to be linear with respect to each of its inputs. That is, the pairing function verifies:

ê (a.Px + b.Py, Q) = ê P_x, Q)^a ⋅ ê(Py, Q)^b

ê (P, a.Q_x) + b.Q_y) = ê P, Q_x)^a ⋅ ê(P, Q_y)^b

Nondegeneracy: The nondegeneracy property means that for all points . In addition, for all points . If we consider a generator P of and a generator of Q of , the value ê(P, Q) = g is equal to the generator .

Efficiency: There is an efficient algorithm to compute the pairing function.

Galbraith et al. [15] defined three types of pairing functions that can be divided into two families:

Symmetric pairing: It verifies .
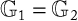Asymmetric pairing: It verifies 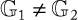This pairing function can be further classified based on the existence, or not, of an efficient homomorphism .

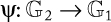Menezes, Okamoto, and Vanstone [26] used a symmetric pairing function to solve the ECDLP. They considered ê and the point Q = x.P. Their idea consists of transposing the ECDLP to a DLP in . They assumed that they have an efficient algorithm to solve the DLP in and they used:

Q =	x.P ⇔ ê(P,Q) =ê P, P)^x
	⇔ h = g^x where h = ê (P, Q) and g = ê (P, P)

As a consequence, the security level of ê will be related to the hardness of solving the DLP in the groups , and . It is closely related to the groups being selected, as some of them make the DLP easier. To understand how to define this security level in practice, the investigation of the structures of , , and is necessary.

Before specifying the structures of , , and , it is necessary to review some definitions related to elliptic curves. We first define the subgroup of q-torsion points as the subgroup of points having the order q. The q-torsion subgroup defined over an elliptic curve E() is denoted by . If p does not divide q, there is a theorem that states that it exists an integer k such that is isomorphic to ([27], Chapter 3, Theorem 3.2). The smallest integer k verifying the previous theorem is called the embedding degree of the curve E() respectively to q.

Let E() denote the elliptic curve defined over the finite prime field . and correspond mostly to the q-torsion subgroups of and E() and , where k is the embedding degree of the curve E() is a multiplicative subgroup of relative to q. Meanwhile, of order q [28].

For example, assume that the prime order p of is 512 bits long, the order q is 160 bits long while the embedding degree relatively to q of the curve E() is 2. The pairing function ê is then defined over the subgroups , , and of order q. The security level of ê is defined respectively to the hardness of solving DLP in . As is a subgroup of which has an order of 1024 bits, DLP hardness in is defined respectively to this 1024-bit order. That is, the pairing ê security level is equivalent to an RSA key of 1024 bits length, and so to a security level of 80 bits with respect to Table 12.1.

In practice, bilinear mapping is derived from the Weil or Tate pairing ([29], Chapter 9). We use the definition given by El-Mrabet [28] to describe these two types of pairing. First, we define a rational function f on the points of an elliptic curve. f takes as input two variables x and y, which represent the coordinates of a point. Then, we specify the divisor of this function Div( f ) as a formal sum that returns information about the zeros and poles of f. To describe the Weil and Tate pairings, we use the function f_q,r that verifies: Div( f_q,r) = q.[R] − (q − 1).[P_∞]. The two types of pairing will be defined as follows:

•

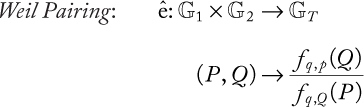
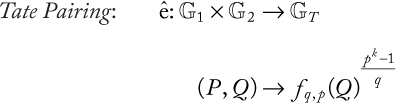
These two formulas will not be used in this chapter. However, interested readers can refer to the books [14], [27], and [29] for a detailed mathematical description of divisors and pairings.

12.2.3 Examples of ID-Based Encryption Schemes

In this section, we start by presenting some well-known ID-based encryption algorithms. The first scheme uses a classical key construction. That is, the public key is a point derived from station’s identity using a hash-to-point function, while the private key is computed as Priv_ID = s.Pub_ID, s is PKG’s secret. The second encryption scheme is the Boneh and Boyen encryption algorithm, which uses the Boneh and Boyen key derivation method (Section 12.2.3.2). The third presented scheme is Chen et al. encryption scheme which relies on Sakai-Kasahara key construction (Section 12.2.3.3). All these IBE schemes’ security is based on the bilinear Diffie–Hellman (BDH) problem, which consists of computing ê(P, P)^abc, given the points P, a.P, b.P, and c.P and the symmetric pairing ê.

12.2.3.1 Boneh and Franklin Encryption Scheme

Boneh and Franklin [18] proposed in 2001 an IBE scheme using symmetric pairing function. They define two hash functions H₁ and H₂ such that: and . So, Boneh and Franklin IBC-PEs are . The PKG computes the user’s public key as Pub_ID =H₁(ID). Then, the PKG generates the corresponding private key using a local secret value .

To encrypt an M ∈{0, 1}ⁿ message using the public key Pub_ID, a user generates a secret random and computes the ciphertext C as

C =(U,V) ( =k.P, M ⊕ H₂ (ê(Pub_ID, P _pub )^k ))

The decrypting entity deciphers the received message as follows:

M = V ⊕ H₂ (ê(Priv_ID, U ))

12.2.3.2 Boneh and Boyen Encryption Schemes

Boneh and Boyen [30] proposed an IBE scheme using a symmetric pairing function. They define two hash functions H₁ and H₂ such that: and . In addition, they define three points that are computed as P₁ =α.P, P₂ =β.P, and P₃ =ϒ.P where α, β, and ϒ are secrets selected by the PKG in . From P₁ and P₂, they compute v =ê(P₁, P₂), which is part of the IBC-PEs. So, Boneh and Boyen public elements are . The PKG computes the user’s public key as Pub_ID =H₁(ID). However, the private key is computed as the couple of points Priv_ID = (Priv₁, Priv₂) = (Pub_ID.r.P₁ + α.P₂ +r.P₃, r.P) where r is a random number selected by PKG.

To encrypt a message M ∈{0, 1}ⁿ using the public key Pub_ID, a user generates a secret random and computes the ciphertext as the tuple C = (c, C₀, C₁), where c = M ⊕H₂(v^k), C₀ = k.P, and C₁ = Pub_ID.k.P₁ + k.P₃. The deciphering entity starts by computing 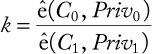. Then, it recovers M as M =c ⊕H₂(v^k).

12.2.3.3 Chen et al. Encryption Scheme

Chen et al. [31] presented an IBE scheme using a symmetric pairing function. They define two hash functions H₁ and H₂ such that and {0, 1} ^l , where l is the size in bits of the message M that is going to be ciphered. A user public key is computed as Pub_ID = H₁(ID) and its corresponding private key is generated by the PKG using the Sakai–Kasahara key generation scheme, i.e., Priv_ID = (1/(Pub_ID + s)).P. In order to encrypt M, the ciphering station chooses a random number and executes the following steps:

U = k. (P_pub + pub_ID. P)
n = H₂(g^k)
V = M ⊕ n

The ciphered message is the pair . The recipient of (U,V) computes first = H₂(ê(U, Priv_ID)). Then, it recovers the message M as: M = V ⊕ n.

12.2.4 Examples of ID-Based Signature Algorithms

In this section, we present three different signature schemes that rely on pairing computation.

12.2.4.1 Paterson Signature Scheme

Paterson [23] proposed, in 2002, an IBS scheme using ECC and a symmetric pairing function. He defines three hash functions H₁, H₂, and H₃ such that: , and So, Paterson IBC-PEs are . The PKG computes the user’s public key as Pub_ID = H₁(ID). Then, the PKG generates the corresponding private key using a local secret value .

To compute the signature of a message M, a user generates a secret random and computes its signature as the pair , where

R = k.P

S = k^–1 (H₂(M).P + H₃(R).Priv_ID)

The signature verifier has only to compare to ê(R, S) to (ê(P, P)^H2(M). ê(P_pub, Pub_ID)^H₃(R). The two values must be equal in order to consider the signature as valid.

12.2.4.2 Hess Signature Scheme

Hess [24] presented an ID-based signature scheme in 2003. Hess signature relies on a symmetric pairing function. His signature scheme keeps the Paterson public parameters definition, but it replaces H₂ and H₃ with a new hash function that we denote as .

In order to sign a message M, the user chooses an arbitrary point and a random number . Then, he or she executes the following steps:

r = ê(P₁, P)^k
v = H₄(M, r)
U = v.Priv_ID + k.P₁

The signature is formed by the pair The signature verifier then has to compute:

r = ê(U, P). ê(Pub_ID, − P_Pub)^v
The signature is accepted if and only if v = H₄(M, r)

12.2.4.3 Barreto et al. Signature Scheme

Barreto et al. [32] presented their ID-based signature scheme in 2005. Their signature basically uses one asymmetric pairing function. It relies on two hash functions H₁ and H₂ such that: and . So, Barreto et al. IBC-PEs are where where Q_pub = s.Q (s is PKG’s secret). A user public key is computed as Pub_ID = H₁(ID), and its corresponding private key is generated by the PKG as Priv_ID = (1/(Pub_ID + s)).P. In order to sign a message M, the signer chooses a random number and executes the following steps:

n = g^k
h = H₂ (M, n)
S = (k + h)Priv _ID

The signature is formed by the pair . Then, the signature verifier has only to check the equality between h and H₂(M, ê(S, H1(ID)Q + Qpub)g^−h).

12.2.5 Arguments in Favor of IBC

In wireless and mobile networks, such as sensor networks or ad hoc networks, bandwidth, memory, and power consumptions are a big concern, as they directly impact the network and station performances. Consequently, the selection of cryptographic tools for security support must be accurate. Certificates require deploying a PKI and certificate management functions for the generation and delivery of certificates by the CA to successfully authenticated STAs. In addition, periodic downloading of CRLs by STAs from the CA is necessary to verify the validity of certificates.

IBC does not need certificates, CRL, and revocation procedures. With IBC, the key lifetime is bound to a timer, and after its expiration, keys are changed. Bandwidth for exchanging certificates between STAs or downloading CRL is saved. For the derivation of the keys of its peers, STA has only to store the IBC-PEs, extract the hash function from the IBC-PEs, and compute the hash over the identity of the peer. That is, no more memory space is used for storing the certificates.

Table 12.2 presents a comparison between IBC and PKI (based on Paterson and Price [33]). IBC relies on unique identities in order to get different public keys, and so different private keys. However, in a PKI, two different certificates can contain the same identity. That is, a user can have two valid certificates that are used for different purposes. With IBC, the public key of an STA can be used even if its private key has not yet been derived. This can be interesting when an STA ciphers some important data for other STAs and requires that they authenticate to the PKG in order to get the private key for the decryption. Compromising the PKG is very dangerous because the PKG secret will be revealed. Consequently, any station private key can be computed and old encrypted messages can be deciphered. However, when the CA is compromised, old encrypted messages are not affected.

Table 12.2 IBC Comparison to PKI

	IBC	PKI
Trusted entity	PKG	CA
Trust guarantee	None	Certificate
Client identity	Unique and authentic	Authentic
Public-key generator	PKG and clients	CA or client
Private-key generator	PKG	CA or client
Public- and private-key generation times	Can be different	Same time, before certificate issuance
Key escrow attack	Not detected	Detected
Key revocation	Timer	CRLs
Usage range	Local domains	Wide domains
Advantages	No certificates, no CRLs, less storage	No key escrow

12.2.6 Use of IBC in Network Security

As shown above, IBC is not new. Its introduction to networks is, however, quite recent. Seth and Keshav described a hierarchical IBC solution that supports mutual authentication and key revocation mechanisms in delay-tolerant networks (DTNs) [34]. Liu et al. presented, in 2009, an Extensible Authentication Protocol (EAP) authentication method that is adapted for wireless mesh networks [35]. They proposed a scheme that relies on Hess ID-based signature [24]. Boudguiga and Laurent [36] presented, in 2011, a key escrow-resistant authentication scheme for wireless networks that relies on secure tokens. Ben-Othman et al. [37, 38] used IBC to secure the Hybrid Wireless Mesh Protocol (HWMP). They authenticate each HWMP path request and response message thanks to an IBS. Moreover, RFC 6267 [39] presented a variant of the Multimedia Internet Keying (MIKEY) protocol, which relies on an IBC authenticated key exchange. Tan et al. [40] described in their paper a lightweight IBE for body sensor networks (BSNs). Drira et al. [41] also proposed a hybrid authentication scheme relying on symmetric cryptography and IBC to authenticate sensors and mobile nodes in a BSN.

12.3 Conclusion

In this chapter, we present a general introduction to public-key cryptography. We describe ID-based cryptography, which relies on the use of elliptic curve groups. ECC and IBC are attractive for many researchers, as they reduce the size of keys, encryption, and signature schemes. They are well suited for the security applications that are specific to network stations with memory constraints. In addition, IBC removes the cumbersome task of managing PKI and certificates, and consequently, the network overhead is reduced. As such, IBC seems to be a promising solution for security provisioning in wireless networks where every saving in bandwidth and terminal memory is welcome.

References

1. A. Kerckhoffs. Military Cryptography (La cryptographie militaire). Journal of Military Sciences ( Journal des sciences militaires), 9, 5–38, 1883.

2. C. Shannon. Communication Theory and Secrecy Systems. Bell System Technical Journal, 28, 656–715, 1949.

3. G. Vernam. Secret Signaling System. US 1310719A, 8, 1919. Available at http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=5061224.

4. NIST. Data Encryption Standard (DES). 1999. Available at http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf.

5. S. Heron. Advanced Encryption Standard (AES). Network Security, 2009(12), 8–12, 2001. Available at http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf.

6. N. Ferguson, B. Schneier, and T. Kohno. Cryptography Engineering: Design Principles and Practical Applications, vol. 277. New York: Wiley, 2010.

7. J. Viega, P. Chandra, and M. Messier. Network Security with OpenSSL, 1st ed. Sebastopol, CA: O’Reilly & Associates, 2002.

8. R. Housley and T. Polk. Planning for PKI: Best Practices Guide for Deploying Public Key Infrastructure, 1st ed. New York: John Wiley & Sons, 2001.

9. W. Diffie and M. Hellman. New Directions in Cryptography. IEEE Transactions on Information Theory, 22(6), 644–654, 1976.

10. R. Rivest, A. Shamir, and L. Adleman. A Method for Obtaining Digital Signatures and Public-Key Cryptosystem, vol. 21, no. 2. New York: ACM, 1978, pp. 120–126. Available at http://doi.acm.org/10.1145/359340.359342.

11. D. Hankerson, A. Menezes, and S. Vanstone. Guide to Elliptic Curve Cryptography. Secaucus, NJ: Springer-Verlag, 2003.

12. A. Menezes, P.V. Oorschot, and S. Vanstone. Handbook of Applied Cryptography, vol. 106, no. 2. Boca Raton, FL: CRC Press, 1997. Available at http://www.cacr.math.uwaterloo.ca/hac/index.html.

13. J. Hoffstein, J. Pipher, and J. Silverman. An Introduction to Mathematical Cryptography, vol. XVI. Berlin: Springer, 2008.

14. J. Silverman. The Arithmetic of Elliptic Curves, vol. 106. New York: Springer, 2009. Available at http://www.springerlink.com/index/10.1007/978-0-387-09494-6.

15. S. Galbraith, K. Paterson, and N. Smart. Pairings for Cryptographers. Discrete Applied Mathematics, 156(160), 3113–3121, 2008. Available at http://www.sciencedirect.com/science/article/pii/S0166218X08000449.

16. NIST. The Digital Signature Standard. Communications of the ACM, 35(7), 36–40, 1992. Available at http://doi.acm.org/10.1145/129902.129904.

17. A. Shamir. Identity-Based Cryptosystems and Signature Schemes. In Proceedings of CRYPTO 84 on Advances in Cryptology. New York: Springer-Verlag, 1985, pp. 47–53.

18. D. Boneh and M. Franklin. Identity-Based Encryption from the Weil Pairing. In Proceedings of the 21st Annual International Cryptology Conference on Advances in Cryptology, CRYPTO ’01. London: Springer-Verlag, 2001, pp. 213–229. Available at http://portal.acm.org/citation.cfm?id=646766.704155.

19. D. Ratna, B. Rana, and S. Palash. Pairing-Based Cryptographic Protocols: A Survey. 2004. Available at http://eprint.iacr.org/.

20. C. Cocks. An Identity Based Encryption Scheme Based on Quadratic Residues. In Proceedings of the 8th IMA International Conference on Cryptography and Coding. London: Springer-Verlag, 2001, pp. 360–363. Available at http://dl.acm.org/citation.cfm?id=647995.742435.

21. M. Bellare and P. Rogaway. Random Oracles Are Practical: A Paradigm for Designing Efficient Protocols. In Proceedings of the 1st ACM Conference on Computer and Communications Security, ACM CCS ’93, New York, NY, 1993, pp. 62–73. Available at http://doi.acm.org/10.1145/168588.168596.

22. M. Bellare, C. Namprempre, and G. Neven. Security Proofs for Identity-Based Identification and Signature Schemes. Journal of Cryptology, 22(1), 1–61, 2008. Available at http://dx.doi.org/10.1007/s00145-008-9028-8.

23. K. Paterson. ID-Based Signatures from Pairings on Elliptic Curves. Electronics Letters, 38(18), 1025–1026, 2002.

24. F. Hess. Efficient Identity Based Signature Schemes Based on Pairings. In SAC ’02: Revised Papers from the 9th Annual International Workshop on Selected Areas in Cryptography. London: Springer-Verlag, 2003, pp. 310–324.

25. R. Sakai and M. Kasahara. ID Based Cryptosystems with Pairing on Elliptic Curve. Report 2003/054. Cryptology ePrint Archive, 2003. Available at http://eprint.iacr.org/.

26. A. Menezes, T. Okamoto, and S. Vanstone. Reducing Elliptic Curve Logarithms to Logarithms in a Finite Field. IEEE Transactions on Information Theory, 39(5), 1639–1646, 1993. Available at http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=259647.

27. L. Washington. Elliptic Curves: Number Theory and Cryptography, 2nd ed. London: Chapman & Hall/CRC, 2008.

28. N. El-Mrabet. Arithmetic, Performances and Resistance of Pairings to Side Channel Attacks (Arithmetiques des couplages, performance et resistance aux attaques par cannaux caches). PhD dissertation, Montpellier II University, 2009.

29. I. Blake, G. Seroussi, and N. Smart. Advances in Elliptic Curve Cryptography (London Mathematical Society Lecture Note Series). New York: Cambridge University Press, 2005.

30. D. Boneh and X. Boyen. Efficient Selective-ID Secure Identity-Based Encryption without Random Oracles. In Advances in Cryptology—EUROCRYPT 2004, ed. C. Cachin and J. Camenisch, vol. 3027. Lecture Notes in Computer Science Series. Berlin: Springer, 2004, pp. 223–238.

31. L. Chen, Z. Cheng, J. Malone-Lee, and N. Smart. Efficient ID-KEM Based on the Sakai-Kasahara Key Construction. IEEE Proceedings in Information Security, 153(1), 19–26, 2006.

32. P. Barreto, B. Libert, N. McCullagh, and J.-J. Quisquater. Efficient and Provably-Secure Identity-Based Signatures and Signcryption from Bilinear Maps. In Advances in Cryptology—ASIACRYPT 2005, ed. B. Roy, vol. 3788. Lecture Notes in Computer Science Series. Berlin: Springer, 2005, pp. 515–532.

33. K. Paterson and G. Price. A Comparison between Traditional Public Key Infrastructures and Identity-Based Cryptography. Technical Report. Royal Holloway University of London, 2003.

34. A. Seth and S. Keshav. Practical Security for Disconnected Nodes. In 1st IEEE ICNP Workshop on Secure Network Protocols (NPSec 2005), June 2005, pp. 31–36.

35. W. Liu, Y. Shang, and Z. Wang. A Wireless Mesh Network Authentication Method Based on Identity Based Signature. In 5th International Conference on Wireless Communications, Networking and Mobile Computing, 2009 (WiCom ’09), 2009, pp. 1–4.

36. A. Boudguiga and M. Laurent. Key-Escrow Resistant ID-Based Authentication Scheme for IEEE 802.11s Mesh Networks. In 2011 IEEE Wireless Communications and Networking Conference (WCNC 2011), March 2011, pp. 784–789.

37. J. Ben-Othman and Y. Saavedra Benitez. On Securing HWMP Using IBC. In 2011 IEEE International Conference on Communications (ICC), June 2011, pp. 1–5.

38. J. Ben-Othman, L. Mokdad, and Y. Saavedra Benitez. Performance Comparison between IBC-HWMP and Hash-HWMP. In 2011 IEEE Global Telecommunications Conference (GLOBECOM), December 2011, pp. 1–5.

39. V. Cakulev and G. Sundaram. MIKEY-IBAKE: Identity-Based Authenticated Key Exchange (IBAKE) Mode of Key Distribution in Multimedia Internet KEYing (MIKEY). RFC 6267 (Informational). Internet Engineering Task Force, June 2011. Available at http://www.ietf.org/rfc/rfc6267.txt.

40. C.C. Tan, H. Wang, S. Zhong, and Q. Li. IBE-Lite: A Lightweight Identity-Based Cryptography for Body Sensor Networks. IEEE Transactions on Information Technology in Biomedicine, 13(6), 926–932, 2009.

41. W. Drira, E. Renault, and D. Zeglache. A Hybrid Authentication and Key Establishment Scheme for WBAN. Presented at International Conference on Trust Security and Privacy in Computing and Communications, 2012 IEEE TrustCom, June 2012.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 12: Fundamentals of Identity Based Cryptography

Create new playlist

Sign In

Sign Up

12FUNDAMENTALS OF IDENTITY-BASED CRYPTOGRAPHY

AYMEN BOUDGUIGA, MARYLINE LAURENT, AND MOHAMED HAMDI

Keywords