8
THE RSA ALGORITHM
SAAD ANDALIB AND SAIFUL AZAD
Contents
8.3 Applications of the RSA Algorithm
Keywords
Asymmetric key algorithm
Private key
Public key
Public-key decryption
Public-key encryption
RSA
In mid-1977, 1 year after the introduction of public-key cryptography by Diffie and Hellman, three young scientists of the Massachusetts Institute of Technology (MIT) took the concept of public-key cryptography and developed an algorithm that is known as the RSA algorithm. It is named after the surnames of the three inventors, Ron Rivest, Adi Shamir, and Leonard Adleman. In RSA, a pair of keys is generated where one key is revealed to the external world, known as a public key, and the other one is kept secret to the user, known as a private key. For generating keys, the RSA algorithm utilizes a number theory concept that is commonly known as the one-way function. A one-way function is easy to do in one way, but it is very difficult to reverse. Consequently, it is infeasible to derive the private key after knowing the public key of a user. Thus, the secrecy of a message remains intact.
8.1 The Concept
Unlike symmetric key cryptography, it is not mandatory to share any secret key among the parties involved in the secret message exchange. Then the question that may arise in our mind is: How does an asymmetric key ensure secrecy of a message? As mentioned previously, in asymmetric key cryptography, instead of generating a single key (which is usually the case for symmetric key cryptography), it generates a pair of keys. Among them, the public key is publicized and the private key is kept secret. These two keys are mathematically related. Since these keys are generated utilizing a one-way function, it is infeasible to generate a private key after knowing the public key, and vice versa. Again, a message encrypted through a key is not feasible to decrypt utilizing a similar key. Hence, the secrecy of a message is preserved.
Let us assume that Alice and Bob desire to exchange secret messages between themselves using asymmetric key cryptography, especially using the RSA algorithm. They first generate their relevant key sets and publicize the public key so that the other party can access it. The denotations of their public and private keys are PUA and PRA for Alice, and PUB and PRB for Bob. Each of the participants keeps his or her private key secret from the other. When Alice wants to send a message to Bob, she encrypts the message using PUB, which she can access. For any message, M, Alice generates a ciphertext, C, as follows:
C = PUB (M)
After receiving C, Bob can decrypt the message employing his private key, PRB. This can be formally expressed as
M = PRB (C)
Figure 8.1 portrays the steps that can be followed to exchange secret messages using the RSA algorithm. Any third party who intercepts C is not able to reproduce M even though it has access to PUB because:
• In asymmetric key cryptography, it is infeasible to generate one key when you have access to the other key.
• A message that is encrypted through a key is not possible to decrypt utilizing a similar key.

Figure 8.1 Secret message exchange procedure using the RSA algorithm.
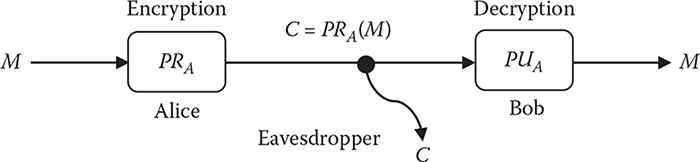
Figure 8.2 Digital signature using the RSA algorithm.
• The public and private keys for any participant are a matched pair and are inverses of each other, i.e.,
M = PRB(PUB(M))
M = PUB(PRB(M))
Consequently, a message that is encrypted using the public key can only be decrypted with its relevant private key.
The RSA algorithm can also be utilized to digitally sign a message so that the recipient has proof of who sent it. In other words, the authenticity of a message can also be checked employing the RSA algorithm. In the case of a digital signature, a message is encrypted using the private key and is decrypted using the relevant public key. Since only a valid sender can have his or her private key, a recipient can assume that the message is sent by the valid sender, which is illustrated in Figure 8.2.
8.2 Operations
The RSA algorithm comprises three steps:
Key generation
Encryption
Decryption
The operations involved in these steps are detailed below.
8.2.1 Key Generation
As mentioned earlier, the RSA algorithm generates a pair of keys. These keys are usually generated employing two large prime numbers (512 bits). The key generation algorithm is stated below:
Select two large prime numbers p and q randomly, such that p ≠ q.
Compute n such that n = p × q.
Compute φ(n) = φ(p) × φ(q) = (p − 1) × (q − 1), where φ is Euler’s totient function.*
Select an integer number e such that 1 < e < φ(n) and gcd(e, φ(n)) = 1, where e and φ(n) are co-prime.
Compute d as the multiplicative inverse of e(mod(φ(n)), i.e., de = 1 mod φ(n).
Publish the pair PU = (e, n) as the participant’s public key.
Keep the pair PE = (d, n) as secret as the participant’s private key.
Relevant pseudocodes for the key generation procedure are discussed below in Algorithms 8.1, 8.2, and 8.3.
Algorithm 8.1: FindE(phi_n)
Begin
e ← 0
do
begin
Choose an integer number e (e must be co-prime of
phi_n)
while (!CheckCoPrime(phi_n, e))
end do-while
return e
End
Algorithm 8.2: FindD(phi_n, e)
Begin
local variables:a, b, x, y, u, v, m, n, q, r, gcd
a ←phi_n
b ←e
x ← 0
y ← 1
u←1
v ← 0
gcd← b
while (a ! = 0)
begin
q ←gcd/a
r ←gcd% a
m ← x - u * q
n ← y - v * q
gcd← a
a ← r
x ← u
y ← v
u ← m
v ← n
end while
if y < 1
begin
y ←phi_n + y
end if
return y
End
Algorithm 8.3: GenerateKey(&n, &e, &d)
Begin
local variables:p, q, phi_n, pt, ct
Enter two prime numbers and stored then in p and q
respectively
n ← Multiply(p,q)
phi_n← Multiply (p-1,q-1)
e ←FindE(phi_n)
d ←FindD(phi_n, e)
/* (e,n) pair is now the public key and (d,n) pair is
now the private key */
End
8.2.2 Encryption
Anyone who wants to send a message can now utilize the public key, (e, n). Recall the previous example, when Alice desires to send a message to Bob; she can now encrypt the message M as follows:
C = Me (mod n)
Alice sends the ciphertext, C, to Bob.
8.2.3 Decryption
After receiving C from Alice, Bob can now decrypt the message utilizing the relative private key. He can find out M using the following expression:
M = Cd (mod n)
Since no one else has the private key of Bob, anyone other than him would not be able to decrypt the message.
Example
Let us look at the following small example to realize how the RSA algorithm works. Suppose Alice desires to send a message to Bob, who generates his keys as follows:
Bob chooses two prime numbers, p = 17 and q = 13.
Then he calculates n such that n = p × q = 17 × 13 = 221.
The value of φ(n) is computed as φ(n) = 16 × 12 = 192.
He selects e = 131.
Bob finds the number d = 107.
Now Bob’s public key is (131, 221) and his private key is (107, 221).
After key generation, Bob publishes his private key and Alice has access to that public key. Let us assume that Alice wants to encrypt the following message, M = 8. Alice can utilize Bob’s public key to produce C, i.e.,
C = 8131 (mod 221) = 70
Bob receives the ciphertext 70 and utilizes his private key to reproduce M as follows.
M = 70107 (mod 221) = 8
Other than Bob, since no one has the private key, no one would be able to decrypt the message.
8.3 Applications of the RSA Algorithm
Although the RSA algorithm is developed to encrypt/decrypt a message, it is very slow in terms of processing speed. It requires a longer time than usual cryptographic algorithms due to generating large prime numbers and performing all the calculations. Moreover, each encryption session usually requires generation of different sets of prime numbers and calculations to prevent the message from being eavesdropped. This is why it is preferred when the message is short. Consequently, it is widely used in Short Message Service (SMS). The RSA algorithm is also utilized to exchange secret keys and to sign a message digitally. It can also be utilized to encrypt a longer message if that is fragmented into small blocks and merged after encryption. The receiver must have the knowledge regarding the fragmentation procedure. He or she could do the opposite and merge after the decryption to produce the original message.
In Chapter 9, another asymmetric key cryptography technique is discussed, elliptic curve cryptography (ECC), which resolves the problem of the RSA algorithm by utilizing a shorter key than RSA and offering comparable performance.
8.4 Implementation Code
#include<iostream>
#include<cmath>
#include<cstdlib>
#include<cstring>
using namespace std;
boolCheckIsPrime(long intnum)
{
if(num< 2) return false;
longinti = 2;
while(i< = num/2)
{
if(!(num% i)) return false;
i++;
}
return true;
}
longint Multiply(long int num1,long int num2)
{
return num1 * num2;
}
boolCheckCoPrime (long int num1, long int num2) {
longint lowest;
if (num1 > num2) lowest = num2;
else lowest = num1;
longinti = 2;
boolcoprime = true;
while (i< lowest) {
if (!(num1% i) && !(num2% i)) coprime = false;
i++;
}
returncoprime;
}
longintFindE(long intphi_n)
{
longint e = 0;
do {
cout<< "Choose an integer number e (e must be coprime
of phi_n): ";
cin>> e;
} while (!CheckCoPrime(phi_n, e));
return e;
}
longintFindD(long intphi_n, long int e)
{
int a = phi_n, b = e;
longint x = 0, y = 1, u = 1, v = 0, m, n, q, r;
longintgcd = b;
while (a ! = 0) {
q = gcd/a;
r = gcd% a;
m = x - u * q;
n = y - v * q;
gcd = a;
a = r;
x = u;
y = v;
u = m;
v = n;
}
if (y < 1) {
cout<< "Choose a suitable "e" value" <<endl;
e = FindE(phi_n);
FindD(phi_n, e);
}
return y;
}
longintEncrypt_Decrypt(long int t, long int e, long
int n)
{
longint rem;
longint x = 1;
while (e ! = 0) {
rem = e % 2;
e = e/2;
if (rem = = 1) x = (x * t)% n;
t = (t * t)% n;
}
return x;
}
voidEncDecStr (long int e, long int n)
{
char *str = new char[1000];
char *str1 = new char[1000];
cout<< " Enter a string: ";
cin>>str;
cout<< "Encrypting using Public Key: " <<endl;
inti = 0;
while (i ! = strlen(str)) {
str1[i] = Encrypt_Decrypt(str[i], e, n);
i++;
}
cout<< str1 <<endl;
}
voidEncDecNum (long int n1, long int n2)
{
longintpn;
cout<< " Enter an integer number: ";
cin>>pn;
cout<<Encrypt_Decrypt(pn, n1, n2) <<endl;
}
voidgenerate_key (long int&n, long int&e, long int&d)
{
longint p, q, phi_n, pt, ct;
do {
cout<< "Enter a prime number: ";
cin>> p;
} while (!CheckIsPrime(p));
do {
cout<< "Enter another prime number: ";
cin>> q;
} while (!CheckIsPrime(q));
n = Multiply(p,q);
cout<< "n is " << n <<endl;
phi_n = Multiply (p-1,q-1);
cout<< "phi_n is " <<phi_n<<endl;
e = FindE(phi_n);
cout<< "e is " << e <<endl;
if (!e) {
cout<< "Choose two suitable prime number"
<<endl;
exit(1);
}
d = FindD(phi_n, e);
cout<< "d is " << d <<endl;
}
int main() {
cout<<endl<<endl<< "##IMPLEMENTATION OF R.S.A
ALGORITHM USING C++##" <<endl<<endl;
longint n, d = 0, e;
generate_key(n, d, e);
cout<< "Public Key : ("<<e<<","<<n<<")" <<endl;
cout<< "Private Key : ("<<d<<","<<n<<")" <<endl;
cout<<endl<< "Press 1: for encrypting numbers & 2: for
encrypting string: ";
int choice;
cin>> choice;
switch (choice) {
case 1:
EncDecNum(e, n);
break;
case 2:
EncDecStr(e, n);
break;
default:
cout<< "Wrong choice. Try again." <<endl;
exit(1);
}
cout<<endl<< "Press 1: for decrypting numbers & 2: for
decrypting string: ";
cin>> choice;
switch (choice) {
case 1:
EncDecNum(d, n);
break;
case 2:
EncDecStr(d, n);
break;
default:
cout<< "Wrong choice. Try again." <<endl;
exit(1);
}
return 0;
}
