3.2.1 Sample

A sample is a set of units or individuals selected from a parent population to provide some useful information about the population. This information can be general shape of distribution, basic statistics, properties of population distribution parameters, or information of some higher moments. Additionally, the sample can be used to estimate test statistics for hypothesis testing. A representative sample can be used to estimate properties of population or to model population parameters.

For instance, the National Sample Survey Organization (NNSO) collects sample data on unemployment by reaching out to limited households, and then this sample is used to provide data for national unemployment.

3.2.2 Sampling Distribution

The distribution of the means of a particular size of samples is called the sampling distribution of means; similarly the distribution of the corresponding sample variances is called the sampling distribution of the variances. These distributions are the fundamental requirements for performing any kind of hypothesis testing.

3.2.3 Population Mean and Variance

Population mean is the arithmetic average of the population data. All the data points contribute toward the population mean with equal weight. Similarly, population variance is the variance calculated using all the data points in the data.

Population mean:

Population Variance:

3.2.4 Sample Mean and Variance

Any subset you draw from the population is a sample. The mean and variance obtained from that sample are called sample statistics. The concept of degrees of freedom is used when a sample is used to estimate distribution parameters; hence, you will see for sample variance that the denominator is different than the population variance.

Sample mean:

Sample variance :

3.2.5 Pooled Mean and Variance

For k sample of size n₁, n₂, n₃, …, n_k taken from the same population, the estimated population mean and variance are defined as follows.

Estimated population mean:

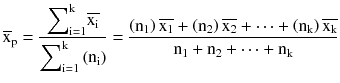
Estimated population variance:

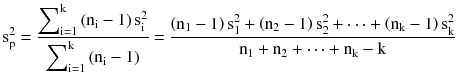
In real-life situations, we usually can have multiple samples drawn from the same population at different points in space/location and time. For example, assume we have to estimate average income of bookshop owner in a city. We will get samples of bookshop owners’ income from different parts of city at different points in time. At a later point of time, we can combine the individual mean and variance from different samples to get an estimate for population using pooled mean and variance.

3.2.6 Sample Point

A possible outcome in a sampling experiment is called a sample point. In many types of sampling, all the data points in the population are not sample points.

Sample points are important when the sampling design becomes complex. The researcher may want to leave some observations out of sampling, alternatively the sampling process by design itself can give less probability of selection to the undesired data point. For example, suppose you have gender data with three possible values—Male, Female, and Unknown. You may want to discard all Unknowns as an error, this is keeping the observation out of sampling. Otherwise, if the data is large and the Unknowns are a very small proportion then the probability to sample them is negligible. In both cases, Unknown is not a sample point.

3.2.7 Sampling Error

The difference between the true value of a population statistic and the sample statistic is the sampling error. This error is attributed to the fact that the estimate has been obtained from the sample.

For example, suppose you know by census data that monthly average income of residents in Boston is $3,000 (the population mean). So, we can say that true mean of income is $3,000. Let’s say that a market research firm performed a small survey of residents in Boston. We find that the sample average income from this small survey is $3,500. The sampling error is then $3,500 - $3,000, which equals $500. Our sample estimates are over-estimating the average income, which also points to the fact that the sample is not a true representation of the population.

3.2.8 Sampling Fraction

The sampling fraction is the ratio of sample size to population size, .

For example, if your total population size is 500,000 and you want to draw a sample of 2,000 from the population, the sampling fraction would be f = 2,000/50,000 = 0.04. In other words, 4% of population is sampled.

3.2.9 Sampling Bias

Sampling bias occurs when the sample units from the population are not characteristic of (i.e., do not reflect) the population. Sampling bias causes a sample to be unrepresentative of the population.

Connecting back to example from sampling error, we found out that the sample average income is way higher than the census average income (true average). This means our sampling design has been biased toward higher income residents of Boston. In that case, our sample is not a true representation of Boston residents.

3.2.10 Sampling Without Replacement (SWOR)

Sampling without replacement requires two conditions to be satisfied;

• Each unit/sample point has a finite non-zero probability of selection

• Once a unit is selected, it is removed from the population

In other words, all the units have some finite probability of being sampled strictly only once.

For instance, if we have a bag of 10 balls, marked with numbers 1 to 10, then each ball has selection probability of 1/10 in a random sample done without replacement. Suppose we have to choose three balls from the bag, then after each selection the probability of selection increases as number of balls left in bag decreases. So, for the first ball the probability of getting selected is 1/10, for the second it’s 1/9, and for the third it’s 1/8.

3.2.11 Sampling with Replacement (SWR)

Sampling with replacement differs from SWOR by the fact that a unit can be sampled more than once in the same sample. Sampling with replacement requires two conditions to be satisfied;

• Each unit/sample point has a finite non-zero probability of selection

• A unit can be selected multiple times, as the sampling population is always the same

In sampling without replacement, the unit can be sampled more than once and each time has the same probability of getting sampled. This type of sampling virtually expands the size of population to infinity as you can create as many samples of any size from this method Connecting back to our previous example in SWOR, if we have to choose three balls with SWR, each ball will have the exact same finite probability of 1/10 for sampling.

The important thing to note here is sampling with replacement technically makes the population size infinite. Be careful while choosing SWR as in most cases each observation is unique and counting it multiple times creates bias in your data. Essentially it will mean you are allowing a repetition of observation. For example, 100 people having the same name, income, age, and gender in the sample will create bias in the dataset.

3.3.1 Data Description

A quick recap from Chapter 2 to describe the following variables in the credit card fraud data,

• custID: A unique identifier for each customer

• gender: Gender of the customer

• state: State in the United States where the customer lives

• cardholder: Number of credit cards the customer holds

• balance: Balance on the credit card

• numTrans: Number of transactions to date

• numIntlTrans: Number of international transactions to date

• creditLine: The financial services corporation, such as Visa, MasterCard, or American Express

• fraudRisk: Binary variable, 1 means customer being frauded, 0 means otherwise

str(data)
 Classes 'data.table' and 'data.frame':   10000000 obs. of  14 variables:
  $ creditLine : int  1 1 1 1 1 1 1 1 1 1 ...
  $ gender     : int  1 1 1 1 1 1 1 1 1 1 ...
  $ state      : int  1 1 1 1 1 1 1 1 1 1 ...
  $ CustomerID : int  4446 59161 136032 223734 240467 248899 262655 324670 390138 482698 ...
  $ NumOfCards : int  1 1 1 1 1 1 1 1 1 1 ...
  $ OutsBal    : int  2000 0 2000 2000 2000 0 0 689 2000 0 ...
  $ DomesTransc: int  31 25 78 11 40 47 15 17 48 25 ...
  $ IntTransc  : int  9 0 3 0 0 0 0 9 0 35 ...
  $ FraudFlag  : int  0 0 0 0 0 0 0 0 0 0 ...
  $ State      : chr  "Alabama" "Alabama" "Alabama" "Alabama" ...
  $ PostalCode : chr  "AL" "AL" "AL" "AL" ...
  $ Gender     : chr  "Male" "Male" "Male" "Male" ...
  $ CardType   : chr  "American Express" "American Express" "American Express" "American Express" ...
  $ CardName   : chr  "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" ...
  - attr(*, ".internal.selfref")=<externalptr>
  - attr(*, "sorted")= chr "creditLine"                                                                      

As stated earlier, we chose outstanding balance as the variable/feature of interest. In the str() output for data descriptive, we can see the outstanding balance is stored in a variable named OutsBal, which is of type integer. Being a continuous variable, mean and variance can be defined for this variable.

3.3.2 Population Mean

Mean is a more traditional statistic for measuring the central tendency of any distribution of data. The mean outstanding balance of our customers in the credit card fraud dataset turns out to be $4109.92. This is our first understanding about the population. Population mean tells us that on average, the customers have an outstanding balance of $4109.92 on their cards.

Population_Mean_P <-mean(data$OutsBal)
cat("The average outstanding balance on cards is ",Population_Mean_P)
 The average outstanding balance on cards is  4109.92

3.3.3 Population Variance

Variance is a measure of spread for the given set of numbers. The smaller the variance, the closer the numbers are to the mean and the larger the variance, the farther away the numbers are from the mean. For the outstanding balance, the variance is 15974788 and standard deviation is 3996.8. The variance by itself is not comparable across different populations or samples. Variance is required to be seen along with mean of the distribution. Standard deviation is another measure and it equals the square root of the variance.

Population_Variance_P <-var(data$OutsBal)
cat("The variance in the average outstanding balance is ",Population_Variance_P)
 The variance in the average outstanding balance is  15974788
cat("Standard deviation of outstanding balance is", sqrt(Population_Variance_P))
 Standard deviation of outstanding balance is 3996.847

3.3.4 Pooled Mean and Variance

Pooled mean and variance estimate population mean and variance when multiple samples are drawn independently of each other. To illustrate the pooled mean and variance compared to true population mean and variance, we will first create five random samples of size 10K, 20K, 40K, 80K, and 100K and calculate their mean and variance.

Using these samples, we will estimate the population mean and variance by using pooled mean and variance formula. Pooled values are useful because estimates from a single sample might produce a large sampling error, whereas if we draw many samples from the same population, the sampling error is reduced. The estimate in a collective manner will be closer to the true population statistics.

In the following R snippet, we are creating five random samples using the sample() function. sample() is an built-in function that’s been used multiple times in the book. Another thing to note is that the sample() function works with some random seed values, so if you want to create reproducible code, use the set.seed(937) function in R. This will make sure that each time you run the code, you get the same random sample.

set.seed(937)
i<-1
n<-rbind(10000,20000,40000,80000,100000)
Sampling_Fraction<-n/nrow(data)
sample_mean<-numeric()
sample_variance<-numeric()
for(i in 1:5)
{
    sample_100K <-data[sample(nrow(data),size=n[i], replace =FALSE, prob =NULL),]
    sample_mean[i]<-round(mean(sample_100K$OutsBal),2)
    sample_variance[i] <-round(var(sample_100K$OutsBal),2)
}

Sample_statistics <-cbind (1:5,c('10K','20K','40K','80K','100K'),sample_mean,sample_variance,round(sqrt(sample_variance),2),Sampling_Fraction)

knitr::kable(Sample_statistics, col.names =c("S.No.", "Size","Sample_Mean","Sample_Variance","Sample SD","Sample_Fraction"))                                                                              

In Table 3-1, basic properties of the five samples are presented. The highest sample fraction is for the biggest sample size. A good thing to notice is that, as the sample size increases, the sample variance gets smaller.

Now let’s use the pooled mean and variance formula to calculate the population mean from the five samples we drew from the population and then compare them with population mean and variance.

i<-1
Population_mean_Num<-0
Population_mean_Den<-0
for(i in 1:5)
{
  Population_mean_Num =Population_mean_Num +sample_mean[i]*n[i]
  Population_mean_Den =Population_mean_Den +n[i]
}

Population_Mean_S<-Population_mean_Num/Population_mean_Den

cat("The pooled mean ( estimate of population mean) is",Population_Mean_S)
 The pooled mean ( estimate of population mean) is 4108.814

The pooled mean is $4,108.814. Now we apply this same process to calculate the pooled variance from the samples. Additionally, we will show the standard deviation as an extra column to make dispersion comparable to the mean measure.

i<-1
Population_variance_Num<-0
Population_variance_Den<-0
for(i in 1:5)
{
  Population_variance_Num =Population_variance_Num +(sample_variance[i])*(n[i] -1)
  Population_variance_Den =Population_variance_Den +n[i] -1
}

Population_Variance_S<-Population_variance_Num/Population_variance_Den

Population_SD_S<-sqrt(Population_Variance_S)

cat("The pooled variance (estimate of population variance) is", Population_Variance_S)
 The pooled variance (estimate of population variance) is 15863765
cat("The pooled standard deviation (estimate of population standard deviation) is", sqrt(Population_Variance_S))
 The pooled standard deviation (estimate of population standard deviation) is 3982.934

The pooled standard deviation is $3,982.934. Now we have both pooled statistics and population statistics. Here, we create a comparison between the two and see how well the pooled statistics estimated the population statistics:

SamplingError_percent_mean<-round((Population_Mean_P -sample_mean)/Population_Mean_P,3)
SamplingError_percent_variance<-round((Population_Variance_P -sample_variance)/Population_Variance_P,3)

Com_Table_1<-cbind(1:5,c('10K','20K','40K','80K','100K'),Sampling_Fraction,SamplingError_percent_mean,SamplingError_percent_variance)

knitr::kable(Com_Table_1, col.names =c("S.No.","Size","Sampling_Frac","Sampling_Error_Mean(%)","Sampling_Error_Variance(%)"))

Table 3-2 shows the comparison of the population mean and the variance against each individual sample. The bigger the sample, the closer the mean estimate to the true population estimate.

Create a same view for pooled statistics against the population statistics. The difference is expressed as a percentage of differences among pooled/sample to the true population statistics.

SamplingError_percent_mean<-(Population_Mean_P -Population_Mean_S)/Population_Mean_P
SamplingError_percent_variance<-(Population_Variance_P -Population_Variance_S)/Population_Variance_P

Com_Table_2 <-cbind(Population_Mean_P,Population_Mean_S,SamplingError_percent_mean)
Com_Table_3 <-cbind(Population_Variance_P,Population_Variance_S,SamplingError_percent_variance)

knitr::kable(Com_Table_2)

knitr::kable(Com_Table_3)

Pooled mean is close to the true mean of the population. This shows that given multiple sample the pooled statistics are more likely to capture true statistics values. You have now seen how a sample so small in size when compared to population gives you estimates so close to the population estimate.

Does this example give you a tool of dealing with big data by using small samples from them? By now you might have started thinking about the cost-benefit analysis of using sampling. This is very relevant to machine learning algorithms churning millions of data points. More data points does not necessarily mean all of them contain meaningful patterns/trends/information. Sampling will try to save you from weeds and help you focus on meaningful datasets for machine learning.

3.4.1 Features of Sampling

• Scientific in nature

• Optimizes time and space constraints

• Reliable method of hypothesis testing

• Allows in-depth analysis by reducing cost

• In cases where population is very large and infrastructure is a constraint, sampling is the only way forward

3.4.2 Shortcomings of Sampling

• Sampling bias can cause wrong inference

• Representative sampling is always not possible due to size, type, requirements, etc.

• It is not exact science but an approximation within certain confidence limits

• In sample survey, we have issues of manual errors, inadequate response, absence of informants, etc.

3.5.1 Types of Non-Probability Sampling

In this section, we briefly touch upon the three major types of non-probability sampling methods. As these techniques are more suited for survey samples, we will not discuss them in detail.

3.6.1 Law of Large Numbers : LLN

In general, as the sample size increases in a test, we expect the results to be more accurate, having smaller deviations in the expected outcomes. The law of large numbers formalizes this with help of the probability theory. The first notable reference to this concept was given by Italian mathematician Gerolamo Cardano in the 16th century, when he observed and stated that empirical statistics get closer to their true value as the number of trials increases.

In later years, a lot of work was done to get different form of the Law of Large Numbers. The example we are going to discuss for a coin toss was first proved by Bernoulli and later he provided proof of his observations. Aleksander Khinchin provided the most popular statement for the Law of Large Numbers, also called the weak law of large numbers. The weak law of large number is alternatively called the law of averages.

3.6.1.3 Steps in Simulation with R Code

Step 1: Assume some value of binomial distribution parameter, p=0.60(say), which we will be be estimating using the Law of Large Numbers

# Set parameters for a binomial distribution Binomial(n, p)                  
# n -> no. of toss                  
# p -> probability of getting a head                  
library(data.table)
n <-100
p <-0.6

In the previous code snippet, we set the true mean for our experiment. Which is to say we know that our population is coming from a binomial distribution with p=0.6. The experiment will now help us estimate this value as the number of experiments increases.

Step 2: Sample a point from binomial distribution (p).

#Create a data frame with 100 values selected samples from Binomial(1,p)                    
set.seed(917);
dt <-data.table(binomial =rbinom(n, 1, p)  ,count_of_heads =0, mean =0)

# Setting the first observation in the data frame                    

ifelse(dt$binomial[1] ==1, dt[1, 2:3] <-1, 0)
 [1] 1

We are using a built-in function rbinom()to sample binomial distributed random variable with parameter, p=0.6. This probability value is chosen such that the coin is biased. If the coin is not biased, then we know the probability of heads is 0.5.

Step 3: Calculate the probability of heads as the number of heads/total no. of coin toss.

# Let's run a experiment large number of times (till n) and see how the average of heads -> probability of heads converge to a value                    

for (i in 2 :n)
  {
    dt$count_of_heads[i] <-ifelse(dt$binomial[i] ==1, dt$count_of_heads[i]<-dt$count_of_heads[i -1]+1, dt$count_of_heads[i -1])
    dt$mean[i] <-dt$count_of_heads[i] /i
}

At each step, we determine if the outcome is heads or tails. Then, we count the number of heads and divide by the number of trials to get an estimated proportion of heads. When you run the same experiment a large number of times, LLN states that you will converge to the probability (expectation or mean) of getting heads in a experiment. For example, at trial 30, we will be counting how many heads so far and divide by 30 to get the average number of heads.

Step 4: Plot and see how the average over the sample is converging to p=0.60.

# Plot the average no. of heads -> probability of heads at each experiment stage                    
plot(dt$mean, type='l', main ="Simulation of average no. of heads",
xlab="Size of Sample", ylab="Sample mean of no. of Heads")
abline(h = p, col="red")

Figure 3-3 shows that as the number of experiments increases, the probability is converging to the true probability of heads (0.6). You are encouraged to run the experiment a large number of times to see the exact convergence. This theorem helps us estimate unknown probabilities by method of experiments and create the distribution for inference testing.

Figure 3-3. Simulation of the coin toss experiment

3.6.2 Central Limit Theorem

The Central Limit Theorem is another very important theorem in probability theory which allows hypothesis testing using the the sampling distribution. In simpler words, the Central Limit Theorem states that sample averages of large number of iterations of independent random variables, each with well-defined means and variances, are approximately normally distributed.

The first written explanation of this concept was provided by de Moivre in his work back in the early 18th century when he used normal distribution to approximate the number of heads from the tossing experiment of a fair coin. Pierre-Simon Laplace published Théorie analytique des probability in 1812, where he expanded the idea of de Moivre by approximating binomial distribution with normal distribution. The precise proof of CLT was provided by Aleksandr Lyapunov in 1901 when he defined it in general terms and proved precisely how it worked mathematically. In probability, this is one the most popular theorems along with the Law of Large Numbers.

In context of this book, we will mathematically state by far the most popular version of the Central Limit Theorem (Lindeberg-Levy CLT).

For a sequence of i.i.d random variables {X1, X2, …} with a well defined expectation and variance (E[Xi] = μ and Var[Xi] = σ²<), as n trends to infinity converge in distribution to a normal N(0, sigma²),

There are other versions of this theorem, such as Lyapunov CLT, Lindeberg CLT, Martingale difference CLT, and many more. It is important to understand how the Law of Large Numbers and the Central Limit Theorem tie together in our sampling context. The Law of Large Numbers states that the sample mean converges to the population mean as the sample size grows, but it does not talk about distribution of sample means. The Central Limit Theorem provides us with the insight into the distribution around mean and states that it converges to a normal distribution for large number of trials. Knowing the distribution then allows us to do inferential testing, as we are able to create confidence bounds for a normal distribution.

We will again set up a simple example to explain the theorem. As a simple example, we will start sampling from a exponential distribution and will show the distribution of sample mean.

3.6.2.1 Steps in Simulation with R Code

Step 1: Set a number of samples (say r=5000) to draw from a mixed population.

#Number of samples                  
r<-5000
#Size of each sample                  
n<-10000

In the previous code, r represented the number of samples to draw, and n represented the number of units in each sample. As per CLT, the larger the number of samples, the better the convergence to a normal distribution.

Step 2: Start sampling by drawing a sample of sizes n (say n=10000 each). Draw samples from normal, uniform, Cauchy, gamma, and other distributions to test the theorem for different distributions. Here, we take an exponential distribution with parameter ()

#Produce a matrix of observations with  n columns and r rows. Each row is one sample                  
lambda<-0.6
Exponential_Samples =matrix(rexp(n*r,lambda),r)

Now, the Exponential_Samples data frame contain the series of i.i.d samples drawn from exponential distribution with the parameter,

Step 3: Calculate the sum, means, and variance of all the samples for each sample.

  all.sample.sums <-apply(Exponential_Samples,1,sum)
  all.sample.means <-apply(Exponential_Samples,1,mean)   
  all.sample.vars <-apply(Exponential_Samples,1,var)

The previous step calculated the sum, mean, and variance of all the i.i.d samples. Now in next step, we will observe the distribution of the sums, means, and variances. As per CLT, we will observe that the mean is following a normal distribution.

Step 4: Plot the combined sum, means, and variances.

par(mfrow=c(2,2))
hist(Exponential_Samples[1,],col="gray",main="Distribution of One Sample")
hist(all.sample.sums,col="gray",main="Sampling Distribution of
       the Sum")
hist(all.sample.means,col="gray",main="Sampling Distribution of the Mean")
hist(all.sample.vars,col="gray",main="Sampling Distribution of
       the Variance")

Figure 3-4 shows the plots of a exponential sample and sum, mean, and standard deviation of the all r samples .

Figure 3-4. Sampling distribution plots

Figure 3-4 shows the distribution of statistics of the samples, i.e., the sum, mean, and variance. The first plot shows the histogram of the first sample from the exponential distribution. You can see the distribution of units in sample is exponential. The visual inspection shows that the statistics estimated from i.i.d samples are following a distribution close to a normal distribution.

Step 5: Repeat this experiment with other distributions and see that the results are consistent with the CLT for all the distributions.

There are some other standard distributions that can be used to validate the results of Central Limit Theorem. Our example just discussed the exponential distribution; you are encouraged to use the following distribution to validate the Central Limit Theorem.

Normal_Samples =matrix(rnorm(n*r,param1,param2),r),

Uniform_Samples =matrix(runif(n*r,param1,param2),r),

Poisson_Samples =matrix(rpois(n*r,param1),r),

Cauchy_Samples =matrix(rcauchy(n*r,param1,param2),r),

Bionomial_Samples =matrix(rbinom(n*r,param1,param2),r),

Gamma_Samples =matrix(rgamma(n*r,param1,param2),r),

ChiSqr_Samples =matrix(rchisq(n*r,param1),r),

StudentT_Samples =matrix(rt(n*r,param1),r))                

It is a good practice to not rely on visual inspection and perform formal tests to infer any properties of distribution. Histogram and a formal test of normality is a good way to establish both visually and by parametric testing that the distribution of means is actually normally distributed (as claimed by CLT).

Next, we perform a Shapiro-Wilk test to test for normality of distribution of means. Other normality tests are discussed in briefly in Chapter 6. One of the most popular non-parametric normality tests is the KS one sample test, which is discussed in Chapter 7.

#Do a formal test of normality on the distribution of sample means                    

  Mean_of_sample_means <-mean (all.sample.means)
  Variance_of_sample_means <-var(all.sample.means)

# testing normality by Shapiro  wilk test  
shapiro.test(all.sample.means)

  Shapiro-Wilk normality test

 data:  all.sample.means
 W = 0.99979, p-value = 0.9263

You can see that the p-value is significant (>0.05) from the Shapiro-Wilk test, which means that we can’t reject the Null hypothesis that distribution is normally distributed. The distribution is indeed normally distributed with a mean = 1.66 and variance = 0.00027.

Visual inspection can be done by plotting histograms. Additionally, for clarity, let’s superimpose the normal density function on the histogram to confirm if the distribution is normally distributed.

x <-all.sample.means
h<-hist(x, breaks=20, col="red", xlab="Sample Means",
main="Histogram with Normal Curve")
xfit<-seq(min(x),max(x),length=40)
yfit<-dnorm(xfit,mean=Mean_of_sample_means,sd=sqrt(Variance_of_sample_means))
yfit <-yfit*diff(h$mids[1:2])*length(x)
lines(xfit, yfit, col="blue", lwd=2)

Figure 3-5. Distribution of sample means with normal density lines

The most important points to remember about the Law of Large Numbers and CLT are:

• As the sample size grows large, you can expect a better estimate of the population/model parameters. This being said, a large sample size will provide you with unbiased and more accurate estimates for hypothesis testing.

• The Central Limit Theorem helps you get a distribution and hence allows you to get a confidence interval around parameters and apply inference testing. The important thing is that CLT doesn’t assume any distribution of population from which samples are drawn, which frees you from distribution assumptions.

3.7.1 Population Statistics

We will look at some basic features of data. These features will be called as population statistics/parameters. We will then show different sampling methods and compare the result with population statistics.

1. Populationdata dimensions

   str() shows us the column names, type, and few values in the column. You can see the dataset is a mix of integers and characters.

   str(data)
    Classes 'data.table' and 'data.frame':   10000000 obs. of  14 variables:
     $ creditLine : int  1 1 1 1 1 1 1 1 1 1 ...
     $ gender     : int  1 1 1 1 1 1 1 1 1 1 ...
     $ state      : int  1 1 1 1 1 1 1 1 1 1 ...
     $ CustomerID : int  4446 59161 136032 223734 240467 248899 262655 324670 390138 482698 ...
     $ NumOfCards : int  1 1 1 1 1 1 1 1 1 1 ...
     $ OutsBal    : int  2000 0 2000 2000 2000 0 0 689 2000 0 ...
     $ DomesTransc: int  31 25 78 11 40 47 15 17 48 25 ...
     $ IntTransc  : int  9 0 3 0 0 0 0 9 0 35 ...
     $ FraudFlag  : int  0 0 0 0 0 0 0 0 0 0 ...
     $ State      : chr  "Alabama" "Alabama" "Alabama" "Alabama" ...
     $ PostalCode : chr  "AL" "AL" "AL" "AL" ...
     $ Gender     : chr  "Male" "Male" "Male" "Male" ...
     $ CardType   : chr  "American Express" "American Express" "American Express" "American Express" ...
     $ CardName   : chr  "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" ...
     - attr(*, ".internal.selfref")=<externalptr>
     - attr(*, "sorted")= chr "creditLine"                                                                                                                                  

2. Population meanfor measures

   1. Outstanding balance: On average each card carries an outstanding amount of $4109.92.

      mean_outstanding_balance <- mean(data$OutsBal)                                
      mean_outstanding_balance                                

      [1] 4109.92

   2. Number of international transactions: Average number of international transactions is 4.04.

      mean_international_trans <- mean(data$IntTransc)                                
      mean_international_trans                                

      [1] 4.04719

   3. Number of domestic transactions: Average number of domestic transactions is very high compared to international transactions; the number is 28.9 ∼ 29 transactions.

      mean_domestic_trans <- mean(data$DomesTransc)                                  
      mean_domestic_trans                                  
      
      [1] 28.93519

3. Population variancefor measures

   1. Outstanding balance:

      Var_outstanding_balance <- var(data$OutsBal)                                
      Var_outstanding_balance                                
      [1] 15974788

   2. Number of international transactions:

      Var_international_trans <- var(data$IntTransc)                                
      Var_international_trans                                
      [1] 74.01109

   3. Number of domestic transactions:

      Var_domestic_trans <- var(data$DomesTransc)                                
      Var_domestic_trans                                
      [1] 705.1033                                

4. Histogram

   1. Outstanding balance:

      hist(data$OutsBal, breaks=20, col="red", xlab="Outstanding Balance",
      main="Distribution of Outstanding Balance")

      

      Figure 3-6. Histogram of outstanding balance

   2. Number of international transactions:

      hist(data$IntTransc, breaks=20, col="blue", xlab="Number of International Transactions",
      main="Distribution of International Transactions")

      

      Figure 3-7. Histogram of number of international transactions

   3. Number of domestic transactions:

      hist(data$DomesTransc, breaks=20, col="green", xlab="Number of Domestic Transactions",
      main="Distribution of Domestic Transactions")

Figure 3-8 shows the mean, variance, and distribution of few important variables from our credit card fraud dataset. These population statistics will be compared to sample statistics to see which sampling techniques provide a representative sample.

Figure 3-8. Histogram of number of domestic transactions

3.7.2 Simple Random Sampling

Simple random sampling is a process of selecting a sample from the population where each unit of population is selected at random Each unit has the same individual probability of being chosen at any stage during the sampling process, and the subset of k individuals has the same probability of being chosen for the sample as any other subset of k individuals.

Simple random is a basic type of sampling, hence it can be a component of more complex sampling methodologies. In coming topics, you will see simple random sampling form an important component of other probability sampling methods, like stratified sampling and cluster sampling.

Simple random sampling is typically without replacement , i.e., by the design of sampling process, we make sure that no unit can be selected more than once. However, simple random sampling can be done with replacement, but in that case the sampling units will not be independent. If you draw a small size sample from a large population, sampling without replacement and sampling with replacement will give approximately the same results, as the probability of each unit to be chosen is very small. Table 3-5 compares the statistics from simple random sampling with and without replacement. The values are comparable, as the population size is very big (∼10 million). We will see this fact in our example.

Advantages:

• It is free from classification error

• Not much advanced knowledge is required of the population

• Easy interpretation of sample data

Disadvantages:

• Complete sampling frame (population) is required to get representative sample

• Data retrieval and storage increases cost and time

• Simple random sample carries the bias and errors present in the population, and additional interventions are required to get rid of those

Function: Summarise

Summarise is a function in the dplyr library. This function helps aggregate the data by dimensions. This works similar to a pivot table in Excel.

• group_by: This argument takes the categorical variable by which you want to aggregate the measures.

• mean(OutsBal): This argument gives the aggregating function and the field name on which aggregation is to be done.

#Population Data :Distribution of Outstanding Balance across Card Type

library(dplyr)

summarise(group_by(data,CardType),Population_OutstandingBalance=mean(OutsBal))
 Source: local data table [4 x 2]

           CardType Population_OutstandingBalance
 1 American Express                      3820.896
 2       MasterCard                      3818.300
 3             Visa                      4584.042
 4         Discover                      4962.420

The call of the summarise function by CardTypeshows the average outstanding balance by card type. Discover cards have the highest average outstanding balance.

Next, we draw a random sample of 100,000 records by using a built-in function sample() from the base library. This function creates a sampling frame by randomly selecting indexes of data. Once we get the sampling frame, we extract the corresponding records from the population data.

Function: Sample

Note some important arguments of the sample() function :

• nrow(data): This tells the size of data. Here it is 10,000,000 and hence it will create an index of 1 to 10,000,000 and then randomly select index for sampling.

• size: Allows users to provide how many data points to sample from the population. In our case, we have set n to 100,000.

• replace: This argument allows users to state if the sampling should be done without replacement (FALSE) or with replacement (TRUE).

• prob: This is vector of probabilities for obtaining the sampling frame. We have set this to NULL, so that they all have the same weight/probability.

set.seed(937)
# Simple Random Sampling Without Replacement                  
library("base")

sample_SOR_100K <-data[sample(nrow(data),size=100000, replace =FALSE, prob =NULL),]

Now, let’s again see how the average balance looks for the simple, random sample. As you can see the order of average balances has been maintained. Note that the average is very close to the population average as calculated in the previous step for population.

#Sample Data : Distribution of Outstanding Balance across Card Type                  

library(dplyr)

summarise(group_by(sample_SOR_100K,CardType),Sample_OutstandingBalance=mean(OutsBal))
 Source: local data table [4 x 2]

           CardType Sample_OutstandingBalance
 1       MasterCard                  3822.632
 2 American Express                  3835.064
 3             Visa                  4611.649
 4         Discover                  4942.690

Function: KS.test()

This is one of the non-parametric tests for comparing the empirical distribution functions of data. This function helps determine if the data points are coming from the same distribution or not. It can be done as one sample test, i.e., the data Empirical Distribution Function (EDF) compared to some preset PDF of distribution (normal, cauchy, etc.), two sample test, i.e., when we want to see if the distribution of two samples is the same or not.

As one of the important features of sampling is to make sure the distribution of data does not change after sampling (except when it is done intentionally), we will use two sample tests to see if the sample is a true representation of the population by checking if the population and sample are drawn from the same distribution.

The important arguments are the two data series and hypothesis to test, two tail, one tail. We are choosing the more conservative two tail test for this example. Two tail test means that we want to make sure the equality is used in the null hypothesis.

#Testing if the sampled data comes from population or not. This makes sure that sampling does not change the original distribution                  
ks.test(data$OutsBal,sample_SOR_100K$OutsBal,alternative="two.sided")
  Two-sample Kolmogorov-Smirnov test

 data:  data$OutsBal and sample_SOR_100K$OutsBal
 D = 0.003042, p-value = 0.3188
 alternative hypothesis: two-sided

The KS test results clearly states that the sample and population have the same distribution. Hence, we can say that the sampling has not changed the distribution. By the nature of sampling, the simple random sampling without replacement retains the distribution of data.

For visual inspection, Figure 3-9 shows the histograms for the population and the sample. As you can see, the distribution is the same for both.

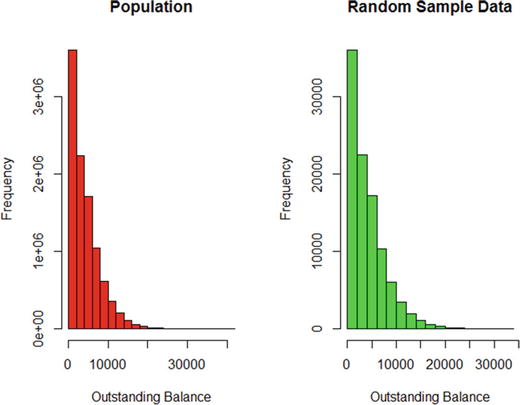
Figure 3-9. Population versus sample (without replacement) distribution

par(mfrow =c(1,2))
hist(data$OutsBal, breaks=20, col="red", xlab="Outstanding Balance",
main="Histogram for Population Data")

hist(sample_SOR_100K$OutsBal, breaks=20, col="green", xlab="Outstanding Balance",
main="Histogram for Sample Data (without replacement)")

Now we will do a formal test on the mean of the outstanding balance from the population and our random sample. Theoretically, we will expect the t-test on means of two to be TRUE and hence we can say that the mean of the sample and population are the same with 95% confidence.

# Lets also do t.test for the mean of population and sample.                  

t.test(data$OutsBal,sample_SOR_100K$OutsBal)

  Welch Two Sample t-test

 data:  data$OutsBal and sample_SOR_100K$OutsBal
 t = -0.85292, df = 102020, p-value = 0.3937
 alternative hypothesis: true difference in means is not equal to 0
 95 percent confidence interval:
  -35.67498  14.04050
 sample estimates:
 mean of x mean of y
  4109.920  4120.737

These results show that the means of population and sample are the same as the p-value of t.testis insignificant. We cannot reject the null hypothesis that the means are equal.

Here we will show you similar testing performed for simple random sample with replacement. As you will see, we don’t see any significant change in the results as compared to simple random sample, as the population size is very big and replacement essentially doesn’t alter the sampling probability of record in any material way.

set.seed(937)
# Simple Random Sampling With Replacement                  
library("base")

sample_SR_100K <-data[sample(nrow(data),size=100000, replace =TRUE, prob =NULL),]

In this code, for simple random sampling with replacement, we set replace to TRUE in the sample function call.

The following code shows how we performed the KS test , on distribution of the population and the sample drawn with replacement. The test shows that the distributions are the same and the p-value is insignificant, which fails to reject the null of equal distribution.

ks.test(data$OutsBal,sample_SR_100K$OutsBal,alternative="two.sided")
 Warning in ks.test(data$OutsBal, sample_SR_100K$OutsBal, alternative =
 "two.sided"): p-value will be approximate in the presence of ties

  Two-sample Kolmogorov-Smirnov test

 data:  data$OutsBal and sample_SR_100K$OutsBal
 D = 0.0037522, p-value = 0.1231
 alternative hypothesis: two-sided

We create the histogram of population and sample with replacement . The plots look the same, coupled with a formal KS test, we see both sample with replacement and populations have the same distribution. Be cautious about this when the population size is small.

par(mfrow =c(1,2))
hist(data$OutsBal, breaks=20, col="red", xlab="Outstanding Balance",
main="Population ")

hist(sample_SR_100K$OutsBal, breaks=20, col="green", xlab="Outstanding Balance",
main=" Random Sample Data ( WR)")

Figure 3-10. Population versus sample (with replacement) distribution

The distribution is similar for population and random sample drawn with replacement . We summarize the simple random sampling by comparing the summary results from population, simple random sample without replacement, and simple random sample with replacement.

population_summary <-summarise(group_by(data,CardType),OutstandingBalance_Population=mean(OutsBal))
random_WOR_summary<-summarise(group_by(sample_SOR_100K,CardType),OutstandingBalance_Random_WOR=mean(OutsBal))
random_WR_summary<-summarise(group_by(sample_SR_100K,CardType),OutstandingBalance_Random_WR=mean(OutsBal))
compare_population_WOR<-merge(population_summary,random_WOR_summary, by="CardType")
compare_population_WR <-merge(population_summary,random_WR_summary, by="CardType")

summary_compare<-cbind(compare_population_WOR,compare_population_WR[,OutstandingBalance_Random_WR])
colnames(summary_compare)[which(names(summary_compare) == "V2")] <- "OutstandingBalance_Random_WR"

knitr::kable(summary_compare)                                                                              

Table 3-5 shows that both with and without replacement, simple random sampling gave similar values of mean across card types, which were very close to the true mean of the population.

Key points:

• Simple random sampling gives representative samples from the population.

• Sampling with and without replacement can give different results with different samples sizes, so extra care should be paid to choosing the method when population size is small.

• The appropriate sample size for each problem differ based on the confidence we want with our testing, business purposes, cost benefit analysis, and other reasons. You will get a good understanding of what is happening in each sampling techniques and can choose the best one that suits the problem at hand.

3.7.3 Systematic Random Sampling

Systematic sampling is a statistical method in which the units are selected with a systematically ordered sampling frame. The most popular form of systematic sampling is based on a circular sampling frame , where we transverse the population from start to end and then again continue from start in a circular manner. In this approach the probability of each unit to be selected is the same and hence this approach is sometimes called the equal-probability method. But you can create other systematic frames according to your need to perform systematic sampling.

In this section, we discuss the most popular circular approach to systematic random sampling. In this method, sampling starts by selecting a unit from the population at random and then every Kth element is selected. When the list ends, the sampling starts from the beginning. Here, the k is known as the skip factor , and it’s calculated as follows
where N is population size and n is sample size.

This approach to systematic sampling makes this functionally similar to simple random sampling, but it is not the same because not every possible sample of a certain size has an equal probability of being chosen (e.g., the seed value will make sure that the adjacent elements are never selected in the sampling frame). However, this method is efficient if variance within the systematic sample is more than the population variance .

Advantages:

• Easy to implement

• Can be more efficient

Disadvantages:

• Can be applied when the population is logically homogeneous

• There can be a hidden pattern in the sampling frame, causing unwanted bias

Let’s create an example of systematic sampling from our credit card fraud data.

Step 1: Identify a subset of population that can be assumed to be homogeneous. A possible option is to subset the population by state. In this example, we use Rhode Island, the smallest state in the United States, to assume homogeneity.

For illustration purposes, let’s create a homogeneous set by subsetting the population with the following business logic. Subset the data and pull the records whose international transactions equal 0 and domestic transactions are less than or equal to 3.

Assuming the previous subset forms a set of homogeneous population, the assumption in subsetting is also partially true as the customers who do not use card domestically are likely not to use them internationally at all.

Data_Subset <-subset(data, IntTransc==0&DomesTransc<=3)
summarise(group_by(Data_Subset,CardType),OutstandingBalance=mean(OutsBal))
 Source: local data table [4 x 2]

           CardType OutstandingBalance
 1 American Express           3827.894
 2       MasterCard           3806.849
 3             Visa           4578.604
 4         Discover           4924.235

Assuming the subset has homogeneous sets of cardholders by card type, we can go ahead with systematic sampling. If the set is not homogeneous, then it’s highly likely that systematic sampling will give a biased sample and hence not provide a true representation of the population. Further, we know that the data is stored in R data frame by an internal index (which will be the same as our customer ID ), so we can rely on internally ordered index for systematic sampling.

Step 2: Set a sample size to sample from the population.

#Size of population ( here the size of card holders from Data Subset)                  
Population_Size_N<-length(Data_Subset$OutsBal)

# Set a the size of sample to pull (should be less than N), n. We will assume n=5000                  

Sample_Size_n<-5000

Step 3: Calculate the skip factor using this formula :

The skip factor will give the jump factor while creating the systematic sampling frame. Essentially, with a seed (or starting index) of c, items will be selected after skipping k items in order.

#Calculate the skip factor                  

k =ceiling(Population_Size_N/Sample_Size_n)

#ceiling(x) rounds to the nearest integer thatâ<U+0080><U+0099>s larger than x.                  
#This means ceiling (2.3) = 3                  

cat("The skip factor for systematic sampling is ",k)
 The skip factor for systematic sampling is  62

Step 4: Set a random seed value of index and then create a sequence vector with seed and skip (sample frame). This will take a seed value of index, say i, then create a sampling frame as i,i+k,i+2k …so one until it has a total of n (sample size) indexes in the sampling frame.

r =sample(1:k, 1)
systematic_sample_index =seq(r, r +k*(Sample_Size_n-1), k)

Step 5: Sample the records from the population by sample frame . Once we have our sampling frame ready, it is nothing but list of indices, so we pull those data records corresponding to the sampling frame.

systematic_sample_5K<-Data_Subset[systematic_sample_index,]

Let’s now compare the systematic sample with a simple random sample of the same size of 5000. As from the previous discussion, we know that the simple random sampling is a true representation of the population, so we can use that as a proxy for population properties.

set.seed(937)
# Simple Random Sampling Without Replacement                  
library("base")

sample_Random_5K <-Data_Subset[sample(nrow(Data_Subset),size=5000, replace =FALSE, prob =NULL),]

Here is the result of summary comparison by card type for outstanding balances. The comparison is important to show what differences in mean will appear if we would have chosen a simple random sample instead of a systematic sample.

sys_summary <-summarise(group_by(systematic_sample_5K,CardType),OutstandingBalance_Sys=mean(OutsBal))
random_summary<-summarise(group_by(sample_Random_5K,CardType),OutstandingBalance_Random=mean(OutsBal))

summary_mean_compare<-merge(sys_summary,random_summary, by="CardType")

print(summary_mean_compare)
 Source: local data table [4 x 3]

           CardType OutstandingBalance_Sys OutstandingBalance_Random
 1 American Express               3745.873                  3733.818
 2         Discover               5258.751                  4698.375
 3       MasterCard               3766.037                  3842.121
 4             Visa               4552.099                  4645.664

Again, we will emphasize on testing the sample EDF with population EDF to make sure that the sampling has not distorted the distribution of data. This steps will be repeated for all the sampling techniques, as this ensures that the sampling is stable for modeling purposes.

ks.test(Data_Subset$OutsBal,systematic_sample_5K$OutsBal,alternative="two.sided")
 Warning in ks.test(Data_Subset$OutsBal, systematic_sample_5K$OutsBal,
 alternative = "two.sided"): p-value will be approximate in the presence of
 ties

  Two-sample Kolmogorov-Smirnov test

 data:  Data_Subset$OutsBal and systematic_sample_5K$OutsBal
 D = 0.010816, p-value = 0.6176
 alternative hypothesis: two-sided

The KS test results show that the distribution is the same and hence the sample is a representation of the population by distribution. Figure 3-11 shows the histograms to show how the distribution is for a homogeneous data subset and a systematic sample. We can see that the distribution has not changed drastically.

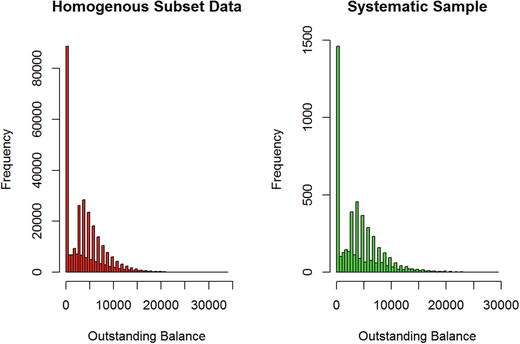
Figure 3-11. Homogeneous population and systematic sample distribution

par(mfrow =c(1,2))
hist(Data_Subset$OutsBal, breaks=50, col="red", xlab="Outstanding Balance",
main="Homogenous Subset Data")

hist(systematic_sample_5K$OutsBal, breaks=50, col="green", xlab="Outstanding Balance",
main="Systematic Sample  ")

Key points:

• Systematic sampling is equivalent to simple random sampling if done on a homogeneous set of data points. Also, a large population size suppresses the bias associated with systematic sampling for smaller sampling fractions.

• Business and computational capacity are important criteria to choose a sampling technique when the population size is large. In our example, the systematic sampling gives a representative sample with a lower computational cost. (There is no call to random number generator, and hence no need to transverse the complete list of records.)

3.7.4 Stratified Random Sampling

When the population has sub-populations that vary, it is important for the sampling technique to consider the variations at the subpopulation (stratum) level and sample them independently at the stratum level. Stratification is the process of identifying homogeneous groups by featuring that group by some intrinsic property. For instance, customers living in the same city can be thought of as belonging to that city stratum. The strata should be mutually exclusive and collectively exhaustive, i.e., all units of the population should be assigned to some strata and one unit can only belong to one strata.

Once we form the stratum then a simple random sampling or systematic sampling is performed at the stratum level independently. This improves the representativeness of sample and generally reduces the sampling error. Dividing the population in stratum also helps you calculate the weighted average of the population, which has less variability than the total population combined.

There are two generally accepted methods of identifying stratified sample size:

• Proportional allocation, which samples equal proportions of the data from each stratum. In this case, the same sampling fraction is applied for all the stratum in the population. For instance, your population has four types of credit cards and you assume that each credit card type forms a homogeneous group of customers. Assume the number of each type of customers in each stratum is N1+N2+N3+N4=total, then in proportional allocation you will get a sample having the same proportion from each stratus (n1/N1=n2/N2=n3/N3=n4/N4=sampling fraction).

• Optimal allocation, which samples proportions of data proportionate to the standard deviation of the distribution of stratum variable. This results in large samples from strata with the highest variability, which means the sample variance is reduced.

Another important feature of stratified sampling is that it makes sure that at least one unit is sampled from each strata, even if the probability of it getting selected is zero. It is recommended to limit the number of strata and make sure enough units are present in each stratum to do sampling.

Advantages:

• Greater precision than simple random sampling of the same sample size

• Due to higher precision, it is possible to work with small samples and hence reduce cost

• Avoid unrepresentative samples, as this method samples at least one unit from each stratum

Disadvantages :

• Not always possible to partition the population in disjointed groups

• Overhead of identifying homogeneous stratum before sampling, adding to administrative cost

• Thin stratum can limit the representative sample size

To construct an example of stratified sampling with credit card fraud data, we first have to check the stratums and then go ahead with sampling from stratum. For our example, we will create a stratum based on the CardType and State variables.

Here, we explain step by step how to go about performing stratified sampling.

Step 1: Check the stratum variables and their frequency in population.

Lets assume CardTypeand State are stratum variables. In other words, we believe the type of card and the state can be used as a criteria to stratify the customers in logical buckets. Here are the frequencies by our stratum variables. We expect stratified sampling to maintain the same proportion of records in the stratified sample.

#Frequency table for CardType in Population                  
table(data$CardType)

 American Express         Discover       MasterCard             Visa
          2474848           642531          4042704          2839917
#Frequency table for State in Population                  
table(data$State)

        Alabama American Samoa        Arizona       Arkansas     California
          20137         162574         101740         202776        1216069
       Colorado    Connecticut       Delaware        Florida        Georgia
         171774         121802          20603          30333         608630
           Guam         Hawaii          Idaho       Illinois        Indiana
         303984          50438         111775          60992         404720
           Iowa         Kansas       Kentucky      Louisiana          Maine
         203143          91127         142170         151715         201918
       Maryland  Massachusetts       Michigan      Minnesota    Mississippi
         202444          40819         304553         182201         203045
       Missouri        Montana       Nebraska         Nevada  New Hampshire
         101829          30131          60617         303833          20215
     New Jersey     New Mexico       New York North Carolina   North Dakota
          40563         284428          81332          91326         608575
           Ohio       Oklahoma         Oregon   Pennsylvania   Rhode Island
         364531         122191         121846         405892          30233
 South Carolina   South Dakota      Tennessee          Texas           Utah
         152253          20449         203827         812638          91375
        Vermont       Virginia     Washington  West Virginia      Wisconsin
         252812          20017         202972         182557          61385
        Wyoming
          20691

The cross table breaks the whole population by the stratum variables , CardType and State. Each stratum represents a set of customers having similar behaviors as they come from the same stratum. The following output is trimmed for easy readability.

#Cross table frequency for population data                  
table(data$State,data$CardType)

                  American Express Discover MasterCard   Visa
   Alabama                    4983     1353       8072   5729
   American Samoa            40144    10602      65740  46088
   Arizona                   25010     6471      41111  29148
   Arkansas                  50158    12977      82042  57599
   California               301183    78154     491187 345545
   Colorado                  42333    11194      69312  48935
   Connecticut               30262     7942      49258  34340
   Delaware                   4990     1322       8427   5864

Step 2: Random sample without replacement from each stratum, consider sampling 10% of the size of the stratum.

We are choosing the most popular way of stratified sampling , proportional sampling. We will be sampling 10% of the records from each stratum.

Function : stratified()

The stratified function samples from a data.frame or a data.table in which one or more columns can be used as a “stratification” or “grouping” variable. The result is a new data.table with the specified number of samples from each group. The standard function syntax is shown here:

stratified(indt, group, size, select = NULL, replace = FALSE,  keep.rownames = FALSE, bothSets = FALSE, ...)                

• group: This argument allows users to define the stratum variables. Here we have chosen CardType and State as the stratum variables. So in Total, we will have 4 (card types) X 52 (states) stratum to sample from.

• size: In general, size can be passed as a number (equal numbers sample from each strata) or a sampling fraction. We will use the sampling fraction of 0.1. For other options type ?stratified in the console.

• replace: This allows you to choose sampling with or without replacement. We have set it as false, which means sampling without replacement.

We will be using this function to perform stratified random sampling.

We can also do the stratified sampling using our standard sample() function as well with following steps:

1. Create subsets of the data by stratum variables.

2. Calculate the sample size for sampling fraction of 0.1, for each stratum.

3. Do a simple random sampling from each stratum for the sample size as calculated.

The previous results and the stratified() results will be the same. But the stratified() function will be faster to execute. You are encouraged to implement this algorithm and try out the other functions.

set.seed(937)
#We want to make sure that our sampling retain the same proportion of the cardtype in the sample                
#Do choose a random sample without replacement from each startum consisting of 10% of total size of stratum                
library(splitstackshape)
stratified_sample_10_percent<-stratified(data, group=c("CardType","State"),size=0.1,replace=FALSE)

Step 3: Check if the proportions of data points in the sample are the same as the population.

Here is the output of stratified sample by CardType, State, and by cross tabulation. The values show that the sampling has been done across the stratum with the same proportion. For example, number of records Alabama and American Express is 4980, in stratified sample the number of Alabama and American Express cardholders is 1/10 of the population, i.e., 498. For all other stratum, the proportion is the same.

#Frequency table for CardType in sample                  
table(stratified_sample_10_percent$CardType)

 American Express         Discover       MasterCard             Visa
           247483            64250           404268           283988
#Frequency table for State in sample                  
table(stratified_sample_10_percent$State)

        Alabama American Samoa        Arizona       Arkansas     California
           2013          16257          10174          20278         121606
       Colorado    Connecticut       Delaware        Florida        Georgia
          17177          12180           2060           3032          60862
           Guam         Hawaii          Idaho       Illinois        Indiana
          30399           5044          11177           6099          40471
           Iowa         Kansas       Kentucky      Louisiana          Maine
          20315           9113          14218          15172          20191
       Maryland  Massachusetts       Michigan      Minnesota    Mississippi
          20245           4081          30455          18220          20305
       Missouri        Montana       Nebraska         Nevada  New Hampshire
          10183           3013           6061          30383           2022
     New Jersey     New Mexico       New York North Carolina   North Dakota
           4056          28442           8133           9132          60856
           Ohio       Oklahoma         Oregon   Pennsylvania   Rhode Island
          36453          12219          12184          40589           3023
 South Carolina   South Dakota      Tennessee          Texas           Utah
          15225           2046          20382          81264           9137
        Vermont       Virginia     Washington  West Virginia      Wisconsin
          25281           2002          20297          18255           6138
        Wyoming
           2069
#Cross table frequency for sample data                  
table(stratified_sample_10_percent$State,stratified_sample_10_percent$CardType)

                  American Express Discover MasterCard  Visa
   Alabama                     498      135        807   573
   American Samoa             4014     1060       6574  4609
   Arizona                    2501      647       4111  2915
   Arkansas                   5016     1298       8204  5760
   California                30118     7815      49119 34554
   Colorado                   4233     1119       6931  4894
   Connecticut                3026      794       4926  3434
   Delaware                    499      132        843   586

You can see that the proportion has remained the same. Here, we compare the properties of sample and population. The summarise() function shows the average of outstanding balance by strata. You can perform a pairwise t.test to see that the sampling has not altered the means of outstanding balance belonging to each strata. You are encouraged to do testing on the means by t.test(), as shown in the simple random sampling section.

# Average outstanding balance by stratum variables                  
summary_population<-summarise(group_by(data,CardType,State),OutstandingBalance_Stratum=mean(OutsBal))

#We can see below the want to make sure that our sampling retain the same proportion of the cardtype in the sample                  
summary_sample<-summarise(group_by(stratified_sample_10_percent,CardType,State),OutstandingBalance_Sample=mean(OutsBal))

#Mean Comparison by stratum                  
summary_mean_compare<-merge(summary_population,summary_sample, by=c("CardType","State"))

Again, we will do a KS test to compare the distribution of the stratified sample. We can see that the KS test shows that both have the same distribution.

ks.test(data$OutsBal,stratified_sample_10_percent$OutsBal,alternative="two.sided")
  Two-sample Kolmogorov-Smirnov test

 data:  data$OutsBal and stratified_sample_10_percent$OutsBal
 D = 0.00073844, p-value = 0.7045
 alternative hypothesis: two-sided

Figure 3-12 shows the histograms to show how the distribution of outstanding balance looks for the sample and population. The visual comparison clearly shows that the sample is representative of the population.

Figure 3-12. Population and stratified sample distribution

par(mfrow =c(1,2))
hist(data$OutsBal, breaks=50, col="red", xlab="Outstanding Balance",
main="Population ")

hist(stratified_sample_10_percent$OutsBal, breaks=50, col="green", xlab="Outstanding Balance",
main="Stratified Sample")

The distribution plot in Figure 3-12 reemphasizes the test results, both population and stratifies random sample have the same distribution. The stratified random sample is representative of the population.

Key points:

• Stratified sampling should be used when you want to make sure the proportion of data points remains the same in the sample. This not only ensures representativeness but also ensures that all the stratum gets a representation in the sample.

• Stratified sampling can also help you systematically design the proportion of records from each stratum, so you can design a stratified sampling plan to change the representation as per business need. For instance, you are modeling a binomial response function, and the even rate or the proportion of 1 is very small in the dataset. Then you can do a stratified random sampling from stratum (0 or 1 response) and try to sample so that proportion of 1 increases to facilitate modeling.

3.7.5 Cluster Sampling

Many times, populations contain heterogeneous groups that are statistically evident in the population. In those cases, it is important to first identify the heterogeneous groups and then plan the sampling strategy. This technique is popular among marketing and campaign designers, as they deal with characteristics of heterogeneous groups within a population.

Cluster sampling can be done in two ways:

• Single-stage sampling: All of the elements within selected clusters are included in the sample. For example, you want to study a particular population feature that’s dominant in a cluster, so you might want to first identify the cluster and its element and just take all the units of that cluster.

• Two-stage sampling: A subset of elements within selected clusters is randomly selected for inclusion in the sample. This method is similar to stratified sampling but differs in the sense that here the clusters are parent units while in former case it was strata. Strata variables may themselves be divided into multiple clusters on the measure scale.

For a fixed sample size, the cluster sampling gives better results when most of the variation in the population is within the groups, not between them. It is not always straightforward to choose sampling methods. Many times the cost per sample point is less for cluster sampling than for other sampling methods. In these kinds of cost constraints, cluster sampling might be a good choice.

It is important to point out the difference between strata and cluster. Although both are overlapping subsets of the population, they are different in many respects.

• While all strata are represented in the sample; in clustering only a subset of clusters are in the sample.

• Stratified sampling gives best result when units within strata are internally homogeneous. However, with cluster sampling, the best results occur when elements within clusters are internally heterogeneous.

Advantages :

• Cheaper than other methods for data collection, as the cluster of interest requires less cost to collect and store, and requires less administrative cost.

• Clustering takes a large population into account in terms of cluster chunks. Since these groups/clusters are so large, deploying any other technique would be very difficult. Clustering is feasible only when we are dealing with large populations with statistically significant clusters present in them.

• Reduction in variability of estimates is observed with other methods of sampling, but this may not be an ideal situation every time.

Disadvantages :

• Sampling error is high due to the design of the sampling process. The ratio between the number of subjects in the cluster study and the number of subjects in an equally reliable, randomly sampled un-clustered study is called design effect, which causes the high sampling error.

• Sampling bias: The chosen sample in cluster sampling will be taken as representative of the entire population and if that cluster has a biased opinion then the entire population is inferred to have the same opinion. This may not be the actual case.

Before we show you cluster sampling, let’s artificially create clusters in our data by subsetting the data by international transaction. We will subset the data with a conditional statement on international transaction. Here you can see we are artificially creating five clusters.

# Before i explain cluster sampling, lets try to subset the data such that we have clear samples to explain the importance of cluster sampling                  
#Subset the data into 5 subgroups                  
Data_Subset_Clusters_1 <-subset(data, IntTransc >2&IntTransc <5)
Data_Subset_Clusters_2 <-subset(data, IntTransc >10&IntTransc <13)
Data_Subset_Clusters_3 <-subset(data, IntTransc >18&IntTransc <21)
Data_Subset_Clusters_4 <-subset(data, IntTransc >26&IntTransc <29)
Data_Subset_Clusters_5 <-subset(data, IntTransc >34)

Data_Subset_Clusters<-rbind(Data_Subset_Clusters_1,Data_Subset_Clusters_2,Data_Subset_Clusters_3,Data_Subset_Clusters_4,Data_Subset_Clusters_5)

str(Data_Subset_Clusters)
 Classes 'data.table' and 'data.frame':   1291631 obs. of  14 variables:
  $ creditLine : int  1 1 1 1 1 1 1 1 1 1 ...
  $ gender     : int  1 1 1 1 1 1 1 1 1 1 ...
  $ state      : int  1 1 1 1 1 1 1 1 1 1 ...
  $ CustomerID : int  136032 726293 1916600 2180307 3186929 3349887 3726743 5121051 7595816 8058527 ...
  $ NumOfCards : int  1 1 1 1 1 1 1 1 2 1 ...
  $ OutsBal    : int  2000 2000 2000 2000 2000 2000 0 0 2000 2000 ...
  $ DomesTransc: int  78 5 5 44 43 51 57 23 5 15 ...
  $ IntTransc  : int  3 4 3 3 4 4 3 3 4 3 ...
  $ FraudFlag  : int  0 0 0 0 0 0 0 0 0 0 ...
  $ State      : chr  "Alabama" "Alabama" "Alabama" "Alabama" ...
  $ PostalCode : chr  "AL" "AL" "AL" "AL" ...
  $ Gender     : chr  "Male" "Male" "Male" "Male" ...
  $ CardType   : chr  "American Express" "American Express" "American Express" "American Express" ...
  $ CardName   : chr  "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" "SimplyCash® Business Card from American Express" ...
  - attr(*, ".internal.selfref")=<externalptr>

We explicitly created clusters based on the International transactions . The clusters are created to show clustering sampling.

One-stage cluster sampling will mean randomly choosing clusters out of five clusters for analysis. While two-stage sampling will mean randomly choosing few clusters and then doing stratified random sampling from them. In Figure 3-13, we will first create clusters using k-means (discussed in detail in Chapter 6) and then apply stratified sampling, assuming the cluster is the stratum variable.

Figure 3-13. Input data segmented by the set of five classes by number of international transactions

The k-means function creates clusters based on the centroid-based k-means clustering method. Since we have explicitly created five clusters, we will call k-means to form five clusters based on the international transaction values. We already know that the function will give us exactly five clusters as we created in the previous step. This has been done only for illustration purposes’ in real situations, you have to find out the clusters present in the population data .

# Now we will treat the Data_Subset_Clusters as our population                  
library(stats)

kmeans_clusters <-kmeans(Data_Subset_Clusters$IntTransc, 5, nstart =25)

cat("The cluster center are ",kmeans_clusters$centers)
 The cluster center are  59.11837 22.02696 38.53069 47.98671 5.288112

Next, we take a random sample of records just to plot them neatly, as plotting with a large number of records will not be clear.

set.seed(937)
# For plotting lets use only 100000 records randomly chosen from total data.                  
library(splitstackshape)
PlotSample<-Data_Subset_Clusters[sample(nrow(Data_Subset_Clusters),size=100000, replace =TRUE, prob =NULL),]

plot(PlotSample$IntTransc, col = kmeans_clusters$cluster)
points(kmeans_clusters$centers, col =1:5, pch =8)

cluster_sample_combined<-cbind(Data_Subset_Clusters,kmeans_clusters$cluster)

setnames(cluster_sample_combined,"V2","ClusterIdentifier")

Now, we show you the number of records summarized by each cluster. Take note of these numbers, as we will show you the two-stage cluster sampling. The sample will have the same proportion across the clusters.

print("Summary of no. of records per clusters")
 [1] "Summary of no. of records per clusters"
table(cluster_sample_combined$ClusterIdentifier)

      1      2      3      4      5
  67871 128219  75877  44771 974893

Assuming the cluster identifier as the stratum variable and using the stratified() function to draw a sample having 10% of the stratum population respectively.

set.seed(937)
library(splitstackshape)
cluster_sample_10_percent<-stratified(cluster_sample_combined,group=c("ClusterIdentifier"),size=0.1,replace=FALSE)

This step has created the two-stage cluster sample, i.e., randomly selected 10% of the records from each cluster. Let’s plot the clusters with the cluster centers.

print("Plotting the clusters for random sample from clusters")
 [1] "Plotting the clusters for random sample from clusters"
plot(cluster_sample_10_percent$IntTransc, col = kmeans_clusters$cluster)
points(kmeans_clusters$centers, col =1:5, pch =8)

Figure 3-14. Clusters formed by K-means (star sign represents centroid of cluster)

Next is the frequency distribution of cluster sample. Please go back and see the same proportions as on population used for clustering. The stratified sampling at stage two of clustering sampling has ensured that the proportions of data points remain the same, i.e., 10% of the stratum size.

print("Summary of no. of records per clusters")
 [1] "Summary of no. of records per clusters"
table(cluster_sample_10_percent$ClusterIdentifier)

     1     2     3     4     5
  6787 12822  7588  4477 97489

Let’s now show how cluster sampling has impacted the distribution of outstanding balance compared with population and cluster samples.

population_summary <-summarise(group_by(data,CardType),OutstandingBalance_Population=mean(OutsBal))
 Warning in gmean(OutsBal): Group 1 summed to more than type 'integer'
 can hold so the result has been coerced to 'numeric' automatically, for
 convenience.
cluster_summary<-summarise(group_by(cluster_sample_10_percent,CardType),OutstandingBalance_Cluster=mean(OutsBal))

summary_mean_compare<-merge(population_summary,cluster_summary, by="CardType")

print(summary_mean_compare)
 Source: local data table [4 x 3]

           CardType OutstandingBalance_Population
 1 American Express                      3820.896
 2         Discover                      4962.420
 3       MasterCard                      3818.300
 4             Visa                      4584.042
 Variables not shown: OutstandingBalance_Cluster (dbl)

This summary shows how the mean of the outstanding balance impacted by cluster sampling based on the international transactions. For visual inspection, we will create histograms in Figure 3-15. You will see that the distribution is impacted marginally. This could be because the clusters we created assuming international transactions buckets were homogeneous and hence did not have a great impact on the outstanding balance. To be sure, you are encouraged to do a t.test()to see if the means are significantly the same or not.

Figure 3-15. Cluster population and cluster random sample distribution

par(mfrow =c(1,2))
hist(data$OutsBal, breaks=50, col="red", xlab="Outstanding Balance",
main="Histogram for Population Data")

hist(cluster_sample_10_percent$OutsBal, breaks=50, col="green", xlab="Outstanding Balance",
main="Histogram for Cluster Sample Data ")

In other words, clustering sampling is the same as the stratified sampling; the only difference is that the startum variable exists in data and is an intrinsic property of data, while in clustering first we identify clusters and then do random sampling from those clusters.

Key points:

• Cluster sampling should be done only when there is strong evidence of clusters in population and you have strong business reason to justify the clusters and their impact on the modeling outcome.

• Cluster sampling should not be confused with stratified sampling. In stratified sampling, the stratum are formed on the attributes in the dataset while clusters are created based on similarity of subject in population by some relation, e.g., distance from centroid, the same multivariate features, etc. Pay close attention while implementing clustering sampling and clusters need to exist and should make a business case of homogeneity.

3.7.6 Bootstrap Sampling

In statistics, bootstrapping is any sampling method or test or measure that relies on a sampling random sampling with replacement . Theoretically, you can create infinite size population to sample in bootstrapping. It is an advanced topic in statistics and widely used in cases where you have to calculate sampling measure of statistics, e.g., mean, variance, bias, etc., from a sample estimate of the same.

Bootstrapping allows estimation of the sampling distribution of almost any statistic using random sampling methods. Jackknife predates the modern bootstrapping technique. Jackknife estimator of a parameter is found by repeatedly leaving out an observation and calculating the estimate. Once all the observation points are exhausted the average of the estimates is taken as the estimator. For a sample size of N, Jackknife estimate can also be found by aggregating the estimates of each N-1 estimate in the sample. It is important to understand the Jackknife approach, as it provides the basic idea behind the bootstrapping method of a sample metric estimation.

The jackknife estimate of a parameter can be found by estimating the parameter for each subsample and omitting the ith observation to estimate the previously unknown value of a parameter (say ).

The jackknife technique can used to estimate variance of an estimator.
where is the parameter estimate based on leaving out the ith observation, and is the estimator based on all of the sub samples.

In 1977, B. Efron of Stanford University published his noted paper, “Bootstrap Methods: Another Look at the Jackknife.” This paper provides the first detailed account of bootstrapping for a variety of sample metric estimation problems. Statistically, the paper tried to address the following problem: Given a random sample, X= (x1,x2,…Xn) from an unknown probability distribution F, estimate the sampling distribution of some prespecified random variable R(X,F), on the basis of the observed data x. We leave it to you to explore the statistical detail of the method.

When you don’t know the distribution of the population (or you don’t even have a population), bootstrapping comes handy to create hypothesis testing for the sampling estimates. The bootstrapping technique will sample data from the empirical distribution obtained from the sample. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement of the observed dataset (and of equal size to the observed dataset). This comes in very handy when we have a small dataset and we are unsure about the distribution of the estimator to perform hypothesis testing

Advantages :

• Simple to implement; it provides an easy way to calculate standard errors and confidence intervals for complex unknown sampling distributions.

• With increasing computing power, the bootstrap results get better.

• One popular application of bootstrapping is to check for stability of estimates.

Disadvantages :

• Bootstrapping is asymptotically consistent, but does not provide finite sample consistency.

• This is an advanced technique, so you need to be fully aware of the assumptions and properties of estimates derived from the bootstrap methods.

In our R example, we will show how bootstrapping can be used to estimate a population parameter to create a confidence interval around that estimate. This helps in checking the stability of the parameter estimate and perform a hypothesis test. We will be creating the example on a business relevant linear regression methodology.

First, we fit a linear regression model on population data (without intercept). The model will be fit with response variable as an outstanding variable and predictor being number of domestic transactions. Business intuition says that the outstanding balance should be positively correlated with the number of domestic transactions. A positive correlation between dependent and independent variables implies the sign of the linear regression coefficient should be positive.

The coefficient that we get is the true value of the estimate coming from the population. This is the population parameter estimate, as it is calculating the full population.

set.seed(937)
library(boot)
# Now we need the function we would like to estimate                  

#First fit a linear model and know the true estimates, from population data                  
summary(lm(OutsBal ∼0 +DomesTransc, data = data))

 Call:
 lm(formula = OutsBal ∼ 0 + DomesTransc, data = data)

 Residuals:
    Min     1Q Median     3Q    Max
  -7713  -1080   1449   4430  39091

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
 DomesTransc 77.13469    0.03919    1968   <2e-16 ***
 ---
 Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

 Residual standard error: 4867 on 9999999 degrees of freedom
 Multiple R-squared:  0.2792, Adjusted R-squared:  0.2792
 F-statistic: 3.874e+06 on 1 and 9999999 DF,  p-value: < 2.2e-16

You can see the summary of the linear regression model fit on the population data. Now we will take a small sample of population (sampling fraction = 10000/10,000,000=1/1000). Hence, our challenge is to estimate the coefficient of domestic transactions from a very small dataset.

In this context, sampling can be seen as a process to create a larger set of samples from a small set of values to get an estimate of the true distribution of the estimate.

set.seed(937)
#Assume that we are only having 10000 data points and have to do the hypothesis test around significance of coefficient domestic transactions. As the dataset is small we will use the bootstarting to create the distribution of coefficient and then create a confidence interval to test the hypothesis.                  

sample_10000 <-data[sample(nrow(data),size=10000, replace =FALSE, prob =NULL),]

Now we have a small sample to work with. Let’s define a function named Coeff, which will return the coefficient of the domestic transaction variable.

It has a three arguments :

• data: This will be the small dataset that you want to bootstrap. In our case, this is the sample dataset of 10000 records.

• b: A random frame of indexes to choose each time the function is called. This will make sure each time a dataset is selected from a model that’s randomly chosen from the input data.

• formula: This is an optional field. But this will be the functional form of the model which will be estimated by the linear regression.

Here we have just incorporated the formula in the return statement.

# Function to return Coefficient of DomesTransc                  
Coeff =function(data,b,formula){  
# b is the random indexes for the bootstrap sample                  
    d =data[b,]
return(lm(OutsBal ∼0 +DomesTransc, data = d)$coefficients[1])  
# thats for the beta coefficient                  
}

Now we can start bootstrap, so we will be using the function boot() from the boot library. It is very powerful function for both parametric and non-parametric boot strapping. We consider this an advanced topic and will not be covering details of this function. Interested readers are advised to read the function documents from CRAN.

The inputs we are using for our example are:

• data: This is the small sample data we created in the previous step.

• statistics: This is a a function that will return the estimated value of the interested parameter. Here our function Coeff will return the value of coefficient of the domestic transactions.

• R: This the number of bootstrap samples you want to create. A general rule of thumb is the more bootstrap samples you have, the narrower the confidence band.

Here we call the function with R=50.

set.seed(937)
# R is how many bootstrap samples                
bootbet =boot(data=sample_10000, statistic=Coeff, R=50)
names(bootbet)
  [1] "t0"        "t"         "R"         "data"      "seed"     
  [6] "statistic" "sim"       "call"      "stype"     "strata"   
 [11] "weights"

Now plot the histograms and qq plots for the estimated values of the coefficient.

plot                  (bootbet)                

Figure 3-16. Histogram and QQ plot of estimated coefficient

Now, we plot the histogram of parameter estimate. We can see that the bootstrap sample uncovered the distribution of the parameter. We can form a confidence interval around this and do hypothesis testing.

hist(bootbet$t, breaks =5)

Figure 3-17. Histogram of parameter estimate from bootstrap

Here we calculate the mean and variance of the estimated values from bootstrapping. Considering the distribution of coefficient is normally distributed, you can create a confidence band around the mean for the true value.

mean(bootbet$t)
 [1] 76.77636
var(bootbet$t)
          [,1]
 [1,] 2.308969

Additionally, to show how the distribution looks superimposed on a normal distribution from the previous parameters, do this:

x <-bootbet$t
h<-hist(x, breaks=5, col="red", xlab="Boot Strap Estimates",
main="Histogram with Normal Curve")
xfit<-seq(min(x),max(x),length=40)
yfit<-dnorm(xfit,mean=mean(bootbet$t),sd=sqrt(var(bootbet$t)))
yfit <-yfit*diff(h$mids[1:2])*length(x)
lines(xfit, yfit, col="blue", lwd=2)

In Figure 3-18 you can see that we have been able to find the distribution of the coefficient and hence can do hypothesis testing on it. This also provided us a close estimate of the true coefficient. If you look closely, this idea is very close to what jackknife originally proposed. With more computing power, we have just expanded the scope of that method from the mean and standard deviation to any parameter estimation.

Figure 3-18. Histogram with normal density function

The following code does a t.test()on the bootstrap values on coefficients with the true estimate of the coefficient from the population data. This will tell us how close we got to the estimate from a smaller sample and with what confidence we would be able to accept or reject the bootstrapped coefficient.

t.test(bootbet$t, mu=77.13)

  One Sample t-test

 data:  bootbet$t
 t = -1.6456, df = 49, p-value = 0.1062
 alternative hypothesis: true mean is not equal to 77.13
 95 percent confidence interval:
  76.34452 77.20821
 sample estimates:
 mean of x
  76.77636

Key points:

• Bootstrapping is a powerful technique that comes handy when we have little knowledge of the distribution of parameter and only a small dataset is available.

• This technique is advanced in nature and involves a lot of assumptions, so proper statistical knowledge is required to use bootstrapping techniques.