Artificial intelligence: a revue (bring on the dancing girls!)
Game theory versus game-playing AI
Using academic AI in video games: goodness versus fastness (a practical example)
“Good” AI = “good” VGAI??
Players of video games frequently ask for “better AI,” even though most players can’t tell you exactly what they mean by that phrase. Let’s just cut to the chase here: “better AI” can be interpreted as more emotionally intense content, and more believable enemies—in other words, players want more engaging and immersive characters that just plain act right (more on what it means to “act right” in Chapters 2, “The Interaction Hierarchy,” 5, “Gidgets, Gadgets, and Gizbots,” and 6, “Pretending to Be an Individual: Synthetic Personality”). We’re living in interesting times because for perhaps the first time in the history of the game industry, the current generation of hardware will support all of these requests without sacrificing (too much) raw performance—provided we can figure out how to make engaging and immersive characters at all, which ain’t all that easy.
Research has shown that believable, engaging characters have the ability to capture our attention and leave a lasting impression and that a sense of story (i.e., the elements of plot and characterization) is crucial in the creation of engagement and immersion. This sense of story can be augmented in games by good character AI—that is, by characters that offer believable and occasionally surprising performances, just as good fictional characters do.
Let’s face it, video-game characters leave much to be desired when viewed on the same stage as fictional characters. Video-game characters often present as talking heads, or as puppets with their strings being pulled by the game designer—and that’s a good game on a good day. Having said that, creating video-game characters requires a lot more work, a different set of skills, and an advanced level of prowess (and a team of skilled designers, coders, and artists). It isn’t as simple as pulling a well-formed character from a fictional environment and adding him or her to a game. (If only it were … I have a great idea for a game that pits a Ninja Darth Vader against Pirate Barbie in a one-on-one death match!)
Video-game characters are added to the game to help carry the load of storytelling, to move the critical path of the game along, to perform some utility function in the game (shopkeepers, quest givers, enemies to overcome, washer repairmen, or virtual teammates), or any combination of these. Video-game characters could be cast as a subset of what are commonly called artificial characters (or sometimes synthetic characters) and, to a lesser extent, software agents (but not the 007 kind). In video games, however, characters rarely have access to the computational resources that their non-game counterparts enjoy. Even now, despite the recent advances in processing power afforded the new platforms, video-game characters are still not in the right cliques and can’t use the executive washroom. As such, characters found in video games are frequently more brittle, more static, and more predictable. Indeed, video-game characters are often not characters at all—more like puppets than characters, as alluded to above. In some cases, of course, the problem is not the amount of available resources, but the training, talents, and open-mindedness of game designers.
I don’t want to imply that the industry is turning a blind eye to the desires of players. In fact, over the past several years, a trend to bring a more believable emotional experience to games has emerged. Game designers have been exploring ways to increase emotional engagement in their titles for years. The problem isn’t the desire to do so, but in some cases, the manner chosen to do so. As veteran game designer Richard Rouse correctly points out, the belief that advances in graphics and animation are sufficient to carry the load of creating deeper emotional experiences should be viewed with skepticism (when you are too tired to summon up green-skinned rage). In fact, the principle of “amplification through simplification” applies here. This principle states that the relative increase in the audience’s ability to feel an emotional affinity with an artificial character increases as the representation of the character shifts from realistic to iconic—and yes, that may be counterintuitive. In fact, as Rouse goes on to point out, novels can elicit deep emotional responses without using a single graphical element, but a game using deep graphical content and near photo-realistic capabilities often does not.
The problem of creating better AI and better video-game characters is even more complex than a simple lack of resources, the underutilization of those resources that are available, or choosing the wrong method. Even when developers make a commitment to create better games by developing more dynamic AI, they are faced with an age-old and rather difficult problem—one that the academic AI community has been facing for a long time as well: figuring out what it means to be “better,” and then capturing the subject-matter expertise necessary to the creation of this better AI in a form that can be used by an artificial entity.
The problem of creating dynamic character AI gets even more complicated when we begin to consider the concept of player authorship. Player authorship is the result of allowing the player to control the critical path of the game (i.e., the suite of choices made by the player that allow the game to progress from its start to a conclusion), have a permanent (or at least lasting) and perceivable impact on the game world, or solve problems in his or her own way. As such, this is a major goal of game design today. Games do not provide absolute control of their own content as other fictive works do—a concept that is unique to games. Attempting to add this kind of absolute control at the expense of player authorship is disastrous to gameplay (as certain recent game titles prove—names have been changed to protect the annoyingly boring).
The reasons for this are simple, but not necessarily obvious. Some theories of cognitive science claim that we simulate fictional events in the same way that we “rehearse” real-world events: by modeling them in our internal world models. In the case of fiction, however, we create a fictional world model in which to perform these simulations. If that is indeed the case (and my own anecdotal evidence supports this theory, so one out of one of me agrees), trying to impose control on this process shatters the suspension of disbelief that is critical to fictional works. In fact, this mental modeling likely plays a very important role in the maintenance of suspension of disbelief, in the feeling of affinity with characters in the unfolding fiction, and ultimately in the immersion and engagement the complex fiction generates within interactive environments.
So what are we left with? To create better AI in a game, we must create robust video-game characters that can roll with the punches generated by a user who may not be playing to the game’s script. If we expect this better AI to also be believable, these characters must be able to react in a human-like, appropriate manner to the events going on around them. Also, in order to increase the emotional depth in a game, the game’s characters must show emotion appropriately (but this does not imply predictability).
How can we accomplish these lofty goals? Does this sound impossible? It’s not as hard as it sounds. In fact, I could argue that this is no harder than any of the other seemingly impossible problems that have already been solved (real-time path-finding comes to mind). Let’s begin our journey with an examination of academic AI and its overlap with the video-game industry. To that end, we will review important concepts in the study of artificial intelligence, examine the field of game theory, and review the goals of both academic AI and video-game AI. Then, Valued Reader, we will get our hands dirty and create the singularity single-handedly … er, or play Tic Tac Toe.
There are big questions associated with the study of artificial intelligence—hard questions—maybe even $64,000 questions. Questions like
Despite the large number of scientists and philosophers who have considered these questions and ones like it, we don’t yet have complete answers to any of them. In fact, it is difficult just to find a definition of intelligence (let alone for the concept of the human mind) that everyone can agree on—mostly because that guy in the green and yellow shirt three rows over disagrees with everything everyone says. Some dictionaries limit the definition of intelligence to a property possessed exclusively by humans, which is problematic (or possibly just a proof by negation) when we try to extend the conversation to artificial or non-human entities (like the Terminator and Dr. Stephen Colbert, D.F.A.). Even worse for our exploration, however, are recent definitions that claim intelligence is merely the ability to perform computational functions. I don’t know about you, Valued Reader, but I don’t want to have to start worrying about competing with my calculator for my job.
We can console ourselves, however, with the fact that suitable definitions do exist (even if they are not perfect). The American Heritage Dictionary defines intelligence as “the faculty of thought and reason,” or as “the ability to acquire and apply knowledge,” either of which is pretty good for this discussion. I’m willing to bet you a Twinkie, though, that this definition could be better. Hmmm. Maybe if we think about intelligence in terms of mental processes ….
Cognition, when used as a noun, is the collection of mental processes and activities used in perception, learning, recall, thinking, and understanding. Of course, my ability to think, reason, learn, and understand is different from your ability to perform these cognitive tasks (because reasoning about raisins is my raison d’étre, but I digress).
Great! All we have to do to create an artificial intelligence, then, is to create a machine that can think, reason, learn, and understand. Right? Well, sure. As long as we can all agree on, or at least adequately describe, what it means to think, reason, learn, and understand, and we all agree that intelligence is not a single faculty, but rather this collection of mental processes that we now have to define ….
Sigh. Your fancy arguments have led me right back to square one, Valued Reader, and I think you did it on purpose—probably as some misguided attempt at making a point. The problem boils down to the fact that it’s plain hard to create a definition of intelligence that is rigorous enough to stand up to all cases, and that is actually helpful in the evaluation of intelligent machines.
Don’t get discouraged! There is a light at the end of the tunnel—and I promise it isn’t a freight train.
At this point, you might be tempted to say you don’t know what intelligence is, but you know it when you see it. While this may seem like taking the easy way out, the simple fact is we don’t yet understand intelligence very well and we have to leave some leeway in our language so that down the road we can claim we knew all along about things we might discover later. I mean, we can all recognize intelligent behavior when we see it (at least by counter-example). Right? Unfortunately, however, this wait-and-see approach is highly subjective. What if I say a machine is intelligent, and you disagree (clearly wrong-headedly)? And who mediates the dispute if Jimmy Carter is busy?
Luckily for us, a potential answer already exists. A British mathematician named Alan Turing gave a lot of thought to the topics we’ve been exploring. In fact, he wrote one of the seminal papers on machine intelligence called “Computing Machinery and Intelligence” in 1950. In his paper, Turing stayed away from the philosophical black holes associated with defining intelligence and thinking. He believed machines could be intelligent, despite knowing he could not provide an adequate description of intelligence and despite knowing he could not prove machines could be made intelligent. Instead, he provided a test based around the idea of an existence proof—the idea that one intelligent being can recognize intelligent behavior in another.
Turing’s existence proof takes the form of a game, the Imitation Game or the Turing Test. The original game included two phases. In phase one, an interrogator communicates across a neutral, text-only medium with a man and a woman simultaneously, with the interrogator trying to determine the gender of each participant by asking questions and observing their responses. Both the man and the woman are tasked with convincing the interrogator that they are female. The interrogator is not limited in any way—he may ask any question that pops into his head (and should immediately ask if the test makes him look fat) or drill down in a particular subject area of interest (like shoes, or maybe feelings, as long as we have already destroyed any political correctness we may have had going).
During the second phase of Turing’s Imitation Game, a machine that has been programmed to emulate a human (including making mistakes and giving vague answers) and that has been tasked to portray a woman replaces the man. Turing reasoned that if a human interrogator cannot tell the difference between the machine and the man (that is, the machine can deceive the interrogator as many times as the man could), the machine is intelligent.
Subsequent versions of the game condense the test into a single phase in which the interrogator speaks with a human and a machine and tries to determine which is which. This works equally as well as the original version because the test is independent of the details of the experiment (and nicely avoids getting hit in the head with an iron by a spouse). Either version of the test provides us with an objective view of intelligence that is verifiable and repeatable. When we view these facts together, it becomes clear how powerful Turing’s argument is and what a great tool for assessing AI it could be. That is, computational constructs should be evaluated based on the criteria of how well they can mimic human-level performance in cognitive tasks—which may include acting like an idiot in a human way.
Speaking of which, Turing predicted that it would be possible to program a computer to pass the Turing Test by the year 2000. In hindsight, it is clear that this was either a wild-haired guess or his magic eight-ball was out of pixie dust. But although he was wrong in the time limit of the prediction, the Imitation Game allows us to evaluate knowledge-based and expert systems with a reasonable chance of success—even if we have no idea what the heck it means to be intelligent.
It should be noted that even the best program in the history of computing will be easily recognizable as a machine if it responds instantly with the correct answer to the question “What is 17,032 divided by 57?” Similarly, the same program would be instantly recognizable as a machine if it responded inappropriately to the question “What is two plus two?” This implies that the program would have to know when to make mistakes as well as when to delay its responses and by how much. That feature alone might be enough to prove the machine is intelligent. Certainly there are a few Ph.D. dissertations buried in the question.
Why should we hamstring a machine intelligence with human limitations, though? From a practical point of view, we would want the machine to perform as well as a human, but better if it could. Otherwise, we should just have a human do it to begin with. To meet these criteria while still passing the Turing Test, a machine could be programmed to recognize the context of the conversations and react appropriately, e.g., turning down its capabilities for a Turing Test or when believability is maximally important and working at full capacity otherwise.
Turing attempted to provide an answer to the question of what AI is by examining the termination conditions (or the goals) for the pursuit. His test obviously is not successful if the goal of your project is to create a machine intelligence that can prove math theorems that human minds cannot solve. So what is the goal of artificial intelligence? Ha! I’ll bet you thought you could stump me with that one, didn’t you?
Rats! We’re back to talking about definitions again. Unfortunately, there is no widely accepted definition of exactly what AI is (and yes, this is a recurrent theme). There are very good definitions, though, and many of them share common ideas. For our purposes, let’s define artificial intelligence as the branch of information science interested in creating machines that can mimic or model human cognitive abilities well enough that these machines are able to perform in a manner that is indistinguishable from humans who are performing the same tasks (i.e., by the principle underlying the Turing Test).
This brings us to an important question. Is it enough just to mimic human ability? In other words, is a program written to fool humans into thinking it’s intelligent but that has no capability to understand, learn, or think an artificial intelligence? I will answer your questions, Valued Reader, but this is absolutely the last time! Indeed, there is a division in artificial-intelligence research centered on these very issues. Strong AI is concerned with creating machines that are actually intelligent (according to John Searle, who coined the term, in strong AI, the appropriately programmed computer really is a “mind”). In contrast, weak AI is not concerned with producing programs that are truly intelligent, but programs that are really good at problem solving, abstract reasoning, or fooling humans with clever engineering.
It is fair to say that strong AI requires the ability to program a machine to understand, to have tremendous amounts of learning capability, and to have the ability to use knowledge in a particular domain. Weak AI, on the other hand, requires only the implementation of general methods and algorithms and does not create an understanding of the knowledge found in the domain at all. A weak AI may simply be a brute-force search algorithm for mining data, it may be a stimulus response–style chat bot, or a chess program that plays by enumerating all possible board configurations and choosing its move by a state-space search (a brute-force approach that works in finite problem spaces). A strong AI might be a system to read an encyclopedia, digest the information, and create a summary of what has been read.
Okay, but I promised to talk about the goal of AI, didn’t I? I’m a liar like that.
To state or imply that there is a single overarching goal associated with the pursuit of AI is an expression of dishonesty or a lack of understanding or perhaps merely the tequila talking. AI is too broad of a topic to have a single goal. There are goals aplenty for sure, but a single goal? No way—not even if you offer me two Twinkies.
AI is primarily concerned with three broad areas of focus: modeling everyday human tasks, modeling human thinking and reasoning, and tasks that require expertise. It can also be argued that these tasks are subsumed by two even broader areas—knowledge representation and search—but these two pursuits are very broad and are not limited to AI alone. As such, they don’t define AI very well at all in my opinion—unless you want to define AI as, well, everything.
When we attempt to classify which everyday human tasks an intelligent machine must be able to perform, the list is as varied and unbounded as is the group of scientists pursuing such a goal. Nonetheless, any such list of critical human tasks will likely require the following abilities: perception, common-sense reasoning, natural language, robotic control, and due to recent advances in cognitive science, emotional context. Of course, we can argue that many (any) other common human cognitive abilities can be included in this list, but that argument leads us down a garden path of infinite arguments to include just one more ability (or just one more shot of tequila).
We rely on visual and auditory cues to choose our own behaviors and to successfully navigate the world. We augment our hearing with our vision to help us determine meaning and context of conversations (and to eavesdrop). We use smell and taste to warn of danger in our food and water. We use touch when our vision is obscured. These perceptual tasks are simple for humans but are very difficult for a computer to perform (and not just because they don’t have ears, eyes, noses, and fingers, although that certainly makes it harder). In fact, one could argue that we humans have evolved into this position of perceptual dominance.
Our brain can easily deal with the continuous flow of information and has the ability to filter out background noise from the signal. We do this automatically (or at least subconsciously) for the most part. A computer, on the other hand, must first convert the continuous signal into a digital signal. Then it must determine which parts of the signal are safe to ignore and which parts are crucial to the message. This may or may not be easy to program, depending on the problem domain; we still don’t have a clear understanding of how the brain does it so efficiently.
In the past, the pursuit of computer perception has meant either computer vision or speech processing exclusively, but recently researchers have begun to work on smell, taste, and even touch—senses we all know and rely on, but of whose inner workings we have little understanding. Both computer vision and speech processing have taken tremendous leaps forward, and while neither by itself will produce HAL 9000 or Data from Star Trek, we can certainly assert that no such autonomous beings will be produced without these two fields. We will reexamine perception in more detail later in the book when we discuss the problem of creating characters that pretend to be individuals (and what a bunch of liars they are).
Natural language is also critically important to humans (not as important as Twinkies and tequila, surely, but pretty important anyway). Understanding natural language, even if we disregard spoken languages and focus only on the understanding of text, is extremely difficult—especially if your AI has to talk to a four year old. Natural language includes vague linguistic forms, words that can change meanings depending on context, and modes of speech (such as sarcasm) where the meaning of what’s being said is actually the inverse of the meaning of the phrase uttered. Each of these problems is potentially disastrous to the cause of natural language understanding (NLU).
Natural language is made up of four parts: lexical atoms, syntax, semantics, and pragmatics. Simply put, a lexical atom is a basic unit of the language that is contained in an ontology of meaning. In other words, it is a word for which a definition exists; a gesture, like a wave, known to everyone; or a ubiquitous expression, like a smile. Syntax is the set of rules that governs the structure of the language, and semantics are the set of rules that govern how meaning is determined. Pragmatics are the set of rules that govern how the context in which a phrase is used can change the meaning.
We can encode a lexicon with ease. We can write a parser to determine if a phrase is syntactically sound. It is much, much harder, however, to program a computer to correctly process the semantics of a statement, and harder still to allow for pragmatics. As humans, we learn to accomplish these tasks and are able to process phrases in real time with a high degree of accuracy (except, of course, when talking to your significant other, in which case you might as well be speaking in different languages), but even after a lifetime of practice, we still get it wrong at times.
To complicate this problem even further, there are two forms of communication: lexical and creative. Lexical communication describes those expressions that are pulled from a common, ubiquitous lexicon of meaning. Creative communication, on the other hand, describes those expressions that must be parsed for meaning in the context. Looking back to the four parts of natural language, we can see that lexical communication includes lexical atoms, and possibly syntactic rules, and that creative communication includes lexical atoms, syntactic rules, an evaluation of semantics, and an evaluation of pragmatics.
As you might expect, handling lexical communications boils down to a pattern-matching activity, efficient search routines, and building an ontological lexicon. However, these systems are generally fragile because the lexicon must be very deep to accommodate all possible entries—often so deep as to make them impractical in terms of space efficiency and the time it takes to search the large domain. For example, the lexicon would need an entry for “Pass the butter,” “Hand me the butter,” and “Give me the butter” if you wanted the system to be able to understand the three phrases. Of course, some cases can be handled by word equivalencies, but generally speaking, these equivalencies are language and context dependent. For example, “go” and “run” are equivalent when paired with the phrase “to the store for me,” but are clearly not equivalent when paired with the phrase “the computer program.” That is, “go the computer program” is nonsensical, while “go to the store for me” is not.
Creative communications gum up the works even further (possibly by inserting Gummy Bears into the mix). Grammar rules allow for infinite permutations of the set of valid expressions in the language, and though these expressions must be syntactically correct, the rules for determining meaning may not be as well defined, or the meaning of the resulting phrases may be ambiguous outside of a clear context. For example, the phrase “No fruit flies like bananas” is completely ambiguous outside of a context. The phrase can either mean that there is no fruit fly in existence that prefers to eat bananas or that there is no better missile for a food fight than a banana. This example is relatively simple and could obviously be handled with a special case in a lexicon, but how do we handle the grammatical rules that allow for ambiguous phrases in the first place? How do we correctly find the meaning for such cases that we haven’t yet thought of? How do we keep our lexicon’s search space accessible and fast?
It is important to note that the term ambiguous means capable of being understood in two or more possible senses and that the meaning is dependent on the context. In other words, an ambiguous phrase has two possible and equally valid parses in the language’s syntax. Both parses may be clear and have concise meanings as in the preceding example. Humans are quite adept at determining meaning from context—even from implied context, as is the case with many forms of humor and innuendo. We will revisit these topics later in the book when we cover lexical and creative communications in more detail.
Another context-sensitive problem domain is that of common-sense reasoning. Humans are typically good at finding answers to problems in our everyday environments and generalizing these answers to other problems. We consider it common sense that all stove burners may be hot, that all snow is cold, that rain is wet, etc. Computers don’t have this capability. A computer needs a generalized rule for each such topic, and a reasoner that can correctly traverse the set of rules—and even then, vague linguistic terms like “hot,” “cold,” “fairly,” etc. have the capacity to bring such a reasoner to its computational knees. Common-sense reasoning is a major topic of interest in academic AI and is far from a “solved” problem.
Robotic control of complex movements seems to be an even more daunting task than any we’ve yet discussed (which is a pretty tall order). We learn to move our bodies, talk, play sports, dance, paint, etc., with very little difficulty. We often have great difficulty, however, programming complex movements in robotics. While humans can track a ball coming toward us with our eyes, constantly performing estimations of the ball’s trajectory and speed—and at the same time run toward where we think the ball will land with outstretched hands—without conscious effort, a computer cannot easily perform these tasks in isolation. We have enjoyed recent successes in this specific area only after years and years of work. Even a relatively simple task like reaching out in front of you to grab something off the table takes a lot of work and processing for a robot. While this may seem an impossible problem domain to work in, many robotics researchers have made great strides (pun intended) in recent years. We will revisit this topic again as we discuss animation and behavioral control for video-game characters in later chapters.
Recognizing the emotional state of a human user is the point of affective computing, a relatively new area of AI research. The intent is to develop computers that are emotionally intelligent, and that can respond appropriately to the affective-cognitive state of the user. Research following a similar line tries to endow computational agents and characters with a model of human-like personality and emotions. The intent of this kind of research is to increase the affinity that users feel toward these computational characters and increase the acceptance of humans for these agents. We will return to this subject—no, wait, that’s what this entire book is about.
The attempt to formally model human thinking and reasoning describes the second major area of AI research. Scientists working in this area might research game-playing programs, automated reasoners and problem-solvers, planners, machine learning, and biologically inspired human-performance modeling. These subjects are more specialized than those we discussed previously, and far more finite in most cases. However, this area of research can be equally as challenging.
Most games used to research game-playing AI are board games that have a fixed rule set, that have a finite state space, and that are well known to human researchers. The boards themselves are easily and unambiguously represented in a computer, reducing the complexity of the task substantially in comparison to the everyday tasks discussed previously. These systems often rely on state space search algorithms and efficient knowledge-representation techniques. However, these games can generate extremely large state spaces; therefore, fast, efficient search methods are required (even more so if we try to use these techniques in a video game). In addition, these large search spaces require powerful techniques called heuristics for determining what alternatives to pursue in the search. A heuristic is a technique that may sacrifice the ideal of finding the best solution in order to guarantee that a good (but not usually the best) solution will almost always be found.
Automated reasoners and problem solvers typically function in the domain of mathematics and formal logic, but are not limited to these areas. These systems typically evaluate a problem space through a sequence of production rules and can be used to verify theorems, circuit designs, and the syntax of logical expressions, as well as to reduce the complexity of searches. These systems can also be adapted to perform as semantic reasoners in natural language research.
Planning in the AI domain is the attempt to find a sequence of atomic actions that meets an overarching goal. For example, taking a flight from Orlando to New York could be decomposed into the following steps:
Buy ticket.
Pack.
Travel to the airport.
Check luggage.
Find the gate.
Check in with agent at gate and get seat assignments.
Board plane.
Find seat.
Wait for the flight to be over.
Gather carry-on bags.
Deplane.
Find luggage, etc.
While humans create mundane plans like this with ease, programming a computer to emulate this ability is challenging. Goal decomposition usually requires complicated reasoning and a great deal of domain knowledge in a computer. Further, while humans can react to obstacles and instantly modify or form new plans in response to those obstacles, computers have a difficult time determining what steps are still valid and what must be dropped. In other words, Valued Reader, here is another research area in which humans can kick cyborg butt.
Machine learning is another complicated field of study. Learning involves some kind of change in the learner, but it is not obvious exactly what those changes are.
Learning also involves generalization from one context to another and synthesis from one domain to another. We also expect that an intelligence will perform better the second time it sees the same problem as a result of learning. Machine learning has found some success by searching through the problem space to find generalizations suitable for the space. These machine-learning systems can be characterized by the goals of the learner, the method used to symbolically represent knowledge, the problem domain, and the kind of heuristics employed. Machine learners are often specialized and, as a result, can be quite fragile.
Scientists are also intrigued with systems that do not learn by acquiring symbolic language, but rather that model human physiology and function. In this avenue of research, scientists model neurons and neuronal structures. Information is encoded in the interaction between neurons and the organization of the neurons in the system. Learning is accomplished by modifying the structure of these neural networks.
While each of these sub-areas has seen success to some extent, the pursuit of generalized solutions to problems in this space has not been very successful.
Experts are people with a deep understanding of a subject area, a lot of practical experience in a particular field, and a vast amount of specialized knowledge in a particular problem domain. AI researchers are interested in how expertise works in humans and how it can be emulated in computers. Developing these systems requires a knowledge engineer (AI scientist) and a subject-matter expert in most cases. These expert systems are generally restricted to a small, well-studied, and well-understood problem domain, such as diagnosis of liver diseases, or diagnosis of mechanical problems in finite systems. To work well, expert systems must function in a domain that has clear problem-solving strategies.
Generally speaking, the difficult problems in the area of expert systems have been solved, but that is not to say that these systems are bulletproof. On the contrary, these systems generally lack any real knowledge of the domain; instead, they are built around general rules dictated by the human expert and are quite fragile as a result. A human expert facing a problem that doesn’t quite match the rules he routinely uses will generalize the closest rule to the new problem and try out the solution associated with the rule. This is a difficult task for a computer (although this very problem is being worked on in the pursuit of case-based reasoners). The computer must have a heuristic for determining the closeness of the problems and a method for generalizing the solution. Despite the weaknesses, expert systems provide much needed assistance and automation of routine diagnosis-type tasks that may be further verified by a human.
This book won’t be covering the theories and techniques of academic AI in detail, but it does assume a basic understanding of them. (See how I did that? Cool, eh?) There are numerous texts that cover these topics with more depth. Should you find yourself scratching your head, I recommend a brief pause in your reading of this book to review these topics in more detail. Specifically, the following subjects will be discussed as needed as the book develops, without ever fully exploring them in their own right:
Search and heuristics
Knowledge representation
Rules, classification, and inference
Logic and fuzzy logic
State machines
Agent architectures
Learning
I can recommend a few really good books to help you on your path. Just realize that these recommendations are my personal favorites, and that you may not like them as much as I do. (There’s no accounting for taste!) These books do offer solid treatments of the topic, however, and I recommend them as good reference works.
For academic AI books, I like Artificial Intelligence by Elaine Rich and Kevin Knight. In the video-game segment, I really like two books from Charles River Media: Believable Characters for Computer Games, by Penny Baille-de Byl (all of it is great, making it a perfect companion to this book, but for a review of AI topics, check out Chapters 3, 4, and 5); and AI Game Engine Programming by Brian Schwab (also a great companion volume, but unique as it covers academic AI components in line with a treatment of video-game AI specific to genre).
No, this isn’t going to be another run of definitions that don’t work or circular application of rotary reasoning. The good news is that because video-game AI (VGAI) falls squarely in the realm of weak AI, we have a clear goal. What’s more, the goal was defined by Alan Turing, so we get to thumb our noses at the ivory-tower types.
Often, the game industry has a blurry notion of what VGAI is and what its goals are. Some things called “AI” in the industry don’t really seem like AI to an AI guy, and some things we consider to be AI are simply called gameplay programming. The distinction gets lost even further as we start to consider character development in the game industry. There are entire books about developing believable characters that never once leave the realm of modeling and animating in Maya. All that’s fine, as long as the job is getting done.
For the scope of this book, let’s consider all the things we do in a game to increase believability, immersion, and engagement, and to add challenge to the gameplay, as being the scope of VGAI. In that case, many of the reported goals of VGAI don’t really seem to apply. For instance, some developers claim that VGAI should empower the game to appear to make smart decisions, but to do so with a degree of unpredictability. Others say that it should efficiently allow the game to solve problems like navigation and action selection. While I agree that any game that can’t do these things is not likely to be a very good game, I don’t think either statement adequately describes what VGAI should add to a game.
For example, a senior game developer once described a very frustrating problem to me. He had been tasked with adding mistakes to the AI of a popular game to create a more believable and enjoyable play experience. Initial testing, however, generated a lot of feedback about how dumb the AI was. The problem was that he had taken a very VGAI-like approach, and had generated some mistake behaviors that were being called randomly. You may be getting the picture already. Players thought the AI was dumb because it didn’t act right when it made mistakes. It acted weird. The mistakes didn’t seem to be grounded in the context of the situation.
Okay, lesson learned. The goal of VGAI should be to create games that express actions in a manner that appears to be human. Or to put it another way, VGAI must work toward passing the Turing Test. That’s a tall order, and shouldn’t be taken as a call to ignore or even reform traditional VGAI practices, but as a call to expand the scope and consider the implications of VGAI to the player with as much detail as graphics and animation development. In addition, this goal also requires more tailored AI content in the game, which will lead to more design work as well.
It is likely that any attempt to meet this Turing Test level of VGAI will require the active participation and support of the entire development team and upper management. I have learned one very important rule of VGAI in my time in the industry: VGAI without appropriate presentation to the player is a waste of time and computational space, but more on that later.
So this is the section where we talk about how to design a game, right? Wrong.
Game theory has very little to do with developing games, unless you consider that video games are all played by people. Okay, yeah, so that’s a weird statement, huh? Not so much when you think about what game theory actually is (as opposed to the colloquial definitions I see bandied about).
Game theory is the study of how people make decisions in competition. It is technically a branch of mathematics, but is in reality a cross-disciplinary field of study, commonly used by economists, biologists, psychologists, etc., to figure out how people behave in strategic social interactions. The field of game theory was put forth by a book written in 1944 by two gentlemen named John von Neumann and Oskar Morgenstern, Theory of Games and Economic Behavior. You will hear more about von Neumann in later chapters—he’s kind of a big deal to us computer-ish types.
In classical game theory, researchers are interested in a zero sum game in which one player does better at the expense of another player (although today’s game theorists are interested in a much wider class of strategic thinking—e.g., cooperative versus noncooperative, long-instance games, etc.). In many cases, we want to find the equilibria of these situations. In game theory, equilibria are defined as sets of strategies from which players are unlikely to drift away.
Yeah, so, that doesn’t sound like video-game stuff. O contraire, mon frère. Game theory has definite application in the development of video games—especially in complex games with tons of players playing in the same instance (think massively multiplayer online role playing games [MMORPGs]). Game theory can be used to balance abilities, tune non-player character (NPC) behaviors, plan critical paths, etc. The alternative to studying game theory is to develop systems and then test and tune (and test then tune, followed by more testing and tuning, etc.).
In any case, we can use game theory as a tool in designing better character AI. If we know (or can identify) the type of strategy the player is employing, we can tailor NPC behaviors to match (or oppose) that strategy. Alternately, we can design our NPCs to elicit a specific gameplay strategy, which helps provide direction to the player, hopefully in a light-handed manner.
While it may appear that there is a limited amount of overlap between the study of game-playing AI and VGAI, there are tremendous amounts of knowledge and techniques generated by research into game-playing AI that VGAI can exploit. Further, the goals are nearly identical, except for the fact that game-playing AI tends to take more of a strong AI approach and to worry less about believability and fun for the player than is prudent for VGAI. In this section, let’s a take a look at a bit of game-playing AI, develop a bit of XNA code to use it, and then evolve the code base into a basic but playable game. At this point, if you are unfamiliar with XNA, please take a break from this chapter and come play with me in Appendix A, “Getting Started with Microsoft XNA”, as we will rely on the knowledge and skills presented there (not to mention the UI developed there).
Tic-Tac-Toe is a simple game with simple rules—and, as such, is a pretty good place to start looking at this topic. It is played on a 3 × 3 grid by two players. Each player takes a turn, alternating moves, with each trying to be the first to place three tokens in a row (horizontal, vertical, or diagonal).
Due to the small size of the state space, it would be easy to write a program to pack all 255,168 board combinations into a tree and create a function to determine the best move using the appropriate heuristic and proper search algorithm. Knowledge representation is a concept common to all the application areas of academic AI. Knowledge representation is the task of representing information in a computer in a manner that allows for fast and accurate search. The reason for the apparent ubiquity of knowledge representation is that all AI exploits some knowledge domain. Search results into the knowledge domain must be unambiguous. Further, the knowledge base must be changeable and generalizable to accommodate learning. In the case of Tic-Tac-Toe, we would just need to represent all possible board configurations in some kind of linked hierarchical data structure (like a tree or heap) and then come up with a way of easily searching this data for the next board with the best heuristics.
Minimax is a search procedure (and should not be confused with the video game strategy of minmaxing) that is both a depth-first (meaning it looks at a tree node’s children before looking at the node’s siblings) and depth-limited (meaning it only looks so deep before moving on) algorithm. The algorithm starts at the current position in the state space and examines only moves that are possible from that position. Each move is evaluated by a fitness function (heuristic), and the best move is chosen. We assume that this fitness function will return larger numbers to indicate that the move is good for us, smaller numbers to indicate that the move is better for the opponent, and a zero to represent a neutral move.
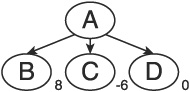
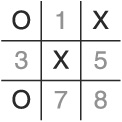
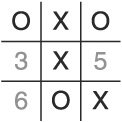
For example, using the tree in Figure 1.1, and assuming a score of 10 means a win and a score of −10 means a lose, we can see that the move with maximum fitness is from A to B. In contrast, the move with the minimum fitness is the move from A to C. If this were the opponent’s turn, the second option would be his best move, and he would choose C.
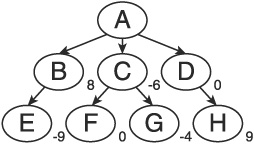
Choosing B may not be the best move, however. Remember that the opponent gets to choose his move next, and he will pick the best move available. Therefore, it is best to examine two plies (a ply is two levels in the tree, constituting one move from each player; Figure 1.1 shows a single ply) together when applying the minimax routine. In Figure 1.2, we see that in the next ply, making move B would allow the opponent to make a very strong move, while making move D would leave us in a very strong position. Therefore, based on an application of minimax that is depth limited to two plies, the AI should choose move D rather than move B.
The pivotal piece of the minimax algorithm is the heuristic used to determine the fitness of the moves. Each search employing this procedure must develop a method of scoring the available boards.
Assuming we developed a good heuristic for ranking each board, would this method work for Tic-Tac-Toe? Yes, provided we could list all 255,168 board configurations and represent that list in memory in an efficient manner. However, it would take a lot of space and would require a large amount of work to specify and verify all the boards (even if we developed equivalencies). From a video-game perspective, neither of those requirements is very attractive. How can we move from a pure academic AI approach to something better suited for a real-time environment?
Maybe we can develop a set of heuristics that would allow us to avoid a brute-force method like the one described and the efficiency pitfalls associated with it. After all, I seriously doubt any Tic-Tac-Toe Grandmasters carry all of those boards around in their head (although chess Grandmasters do carry around portions of the state space in memory—they call it their “book”). In other words, maybe we can move our solution from the realm of a state-space search to that of human-expertise modeling.
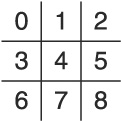
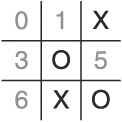
There are a couple of features we can extract from Tic-Tac-Toe that can be exploited to create a simple, fast algorithm that ignores the state space of board configurations. The first few are derived from the board itself. We can exploit the structure of the board by implementing a single-dimension array indexed from 0 .. 8 and labeling each position from 0 to 8 in a left-to-right, top-to-bottom manner (see Figure 1.3). Second, we can see that the positions of the cells in an individual row are easy to calculate given the first cell position. If the first cell is i, then the second cell is i+1, the third cell is i+2, and so on. Also notice that there is a way to calculate cell positions for every column given the first cell. If the first cell in the column is i, then the second cell is i+3, and the third cell is i+6. These two findings are important because if we can find some method of determining whether three tokens are about to appear in a row, we can defend or exploit that fact.
We can also represent the Xs and Os with some numerical values, determine a mathematical relationship between a row or column and some value, and then have an easy test for victory or potential victory. We have to be careful when choosing the numeric values to assign to each token, however. For example, say we choose 0 to represent empty, 1 to represent an X, and 2 to represent an O. In that case, we could be faced with a situation in which we calculate a row’s total value to be 2, but we can’t tell whether the row contains two empty cells and an O or one empty cell and two Xs.
What if we let 2 represent the empty cell, 3 represent the X token, and 5 represent the O token and then multiplied the three cell values instead of summing them? That would avoid the data collision we witnessed in the previous paragraph. Does it meet the primary needs of playing Tic-Tac-Toe, however?
To answer that question, we need to consider two important cases extracted from the set of rules. The first is simple: If it’s my turn and you have two in a row, I should block your move (unless, of course, I can win myself). This rule implies that we need to be able to distinguish two of the same token in the same three-space run as an empty space. Applying the values from above, we can identify two Xs in a set by finding all values of 18 (3 * 3 * 2). Similarly, two Os and a space would multiply to 50 (5 * 5 * 2). In either case, the space we want to put a token in next is the one with a value of 2 (either to win the game or to block the opponent from winning). The second rule covers what happens if neither player can win on the next play. In that case, we should choose the center space if it’s open, then any of the non-corners that are open, then any corner space. We can accomplish this feat by direct lookups into the array.
Guess what? That’s all we need to create an AI with a good chance at beating human players. We don’t need to store game boards or implement minimax because the rules and board are so easy to work with. Furthermore, these rules are essentially the same as what any Tic-Tac-Toe Grandmaster would use. This algorithm isn’t unbeatable, however, and a brute-force implementation would be. So what are we missing?
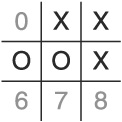
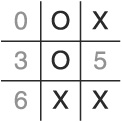
Assuming we allow the player to go first (which puts us in a weak starting position in Tic-Tac-Toe to begin with), there are three strategies of play that guarantee that the player will win against our AI algorithm. For ease of discussion, let’s call the first one the “Center Square Gambit.” In this strategy, the player takes the center square as his first move. If we follow the algorithm described above, the player can keep us from gaining the initiative. In two-player games, initiative can be defined as operating in such a way that the opponent reacts to our moves instead of us being forced to react to his.
Try out this sequence of moves, using the default algorithm:
Put an X in cell 4 (the center square).
Put an O in cell 1 (top-middle square—assuming the AI is in control and following our algorithm).
Put an X in cell 2 (top-right corner).
To block, we must put an O in cell 6 (bottom-left corner).
Put an X in cell 5 (right-middle square).
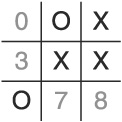
You can see that the game is over. To defend, the AI must block two rows in a single turn: the middle horizontal row (cell three) and the right-most vertical row (cell 8—see Figure 1.4). Since the AI is not allowed to cheat, it loses.
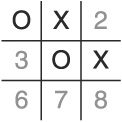
The good news is that there is an easy fix—but it requires a special case that deviates from the two rules we’ve established. When the opponent takes the center square on his first move, we must take a corner square instead of a non-corner square.
To verify my claim, check out this sequence of moves:
Put an X in cell 4.
Put an O in cell 0 (corner instead of middle).
Put an X in cell 2.
To block, put an O in cell 6.
At this point, we’ve guaranteed at least a tie because we’ve regained the initiative and have blocked one of the dual rows used in the Center Square Gambit strategy (see Figure 1.5).
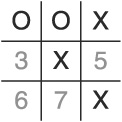
Great! However, the AI is still beatable. (So much for singularity arising from this program!) Let’s call the next strategy the “Corner Gambit.” In this case, the player exploits the rule demanding the AI take the center square if it is open and the rule to take non-corner cells before corner cells by setting up a dual-row attack using either the top or bottom horizontal row and the right or left vertical row.
Let’s examine this strategy:
Put an X in cell 1.
Put an O in cell 4 (by default algorithm).
Put an X in cell 5.
Put an O in cell 3 (following the non-corner cell before corner cell rule).
Put an X in cell 2.
Again, we are facing a board that offers two winning moves to the player—cell 0 and cell 8 (see Figure 1.6). Of course, it is unlikely that a human player would make such a blatant error in tactics as the AI does in step 4, and that’s partially the point: The AI has no ability to choose which rules to follow and which to ignore and when.
To beat this rule, we need to take a corner cell instead of a non-corner cell in the AI’s second move:
Put an X in cell 1.
Put an O in cell 4.
Put an X in cell 5.
Put an O in cell 0.
To block, put an X in cell 8.
Again, we’ve defeated the gambit by regaining the initiative and blocking one of the angles of attack (see Figure 1.7). We can at least tie from this position.
Let’s call the final case the “Sandbagging Gambit.” In this strategy, the player takes the center cell, and the Center Square Gambit strategy causes the AI to choose a corner cell. The player exploits the non-corner rule by taking a non-productive cell.
Let’s try it:
The AI loses again. As shown in Figure 1.8, it can’t defend the two winning moves the player has developed (cell 5 and cell 6).
To counteract this gambit, the AI needs to take the matching corner from its second move. Try this:
Put an X in cell 4.
Put an O in cell 0 (due to the Center Gambit strategy).
Put an X in cell 8.
Put an O in cell 2.
To block, put an X in cell 1.
To block, put an O in cell 7.
As shown in Figure 1.9, we’ve guaranteed a tie game. Yay!
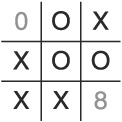
There is another, extremely tricky gambit that can win against this AI. Like the Sandbagging Gambit, it relies on the picking what appears to be a nonproductive space for the player’s second move. Consider this sequence of moves:
Put an X in cell 3.
Put an O in cell 4 (due to the default algorithm).
Put an X in cell 2.
Put an O in cell 1 (following the non-corner cell before corner cell rule).
Put an X in cell 7 to block.
Put an O in cell 5 (following the non-corner cell before corner cell rule).
Put an X in cell 6.
As can be seen in Figure 1.10, the AI loses by letting the player set up two potential three-in-a-row paths. We’ll call this one the Misdirection Gambit.
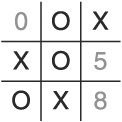
To avoid being sucked in by this ploy, the AI has to recognize the pattern after the player’s third turn. It turns out that if the AI can see this coming, the fix is an easy one. Consider the following moves:
Put an X in cell 3.
Put an O in cell 4 (due to the default algorithm).
Put an X in cell 2.
Put an O in cell 1 (following the non-corner cell before corner cell rule).
Put an X in cell 7 to block.
Put an O in cell 6.
As can be seen in Figure 1.11, placing an O in cell 6 blocks both of the potential paths for a win.
Another variant on the theme of misdirection takes advantage of the directive to choose non-corner spaces before corner spaces. Let’s call this one the “Split Attack Gambit.” Consider the following moves:
Put an X in cell 7.
Put an O in cell 4 (due to the default algorithm).
Put an X in cell 2.
Put an O in cell 1 (following the non-corner cell before corner cell rule).
Put an X in cell 8.
As you can see in Figure 1.12, the AI messed up here. Good thing we didn’t bet our stash of Twinkies on this matchup!
To beat this ruse, consider the following moves:
Put an X in cell 7.
Put an O in cell 4 (due to the default algorithm).
Put an X in cell 2.
Put an O in cell 8.
Figure 1.13 illustrates the block for the Split Attack Gambit; simply choose the corner in the same row as the non-corner X token and in the same column as the corner X token.
By augmenting our algorithm with special rules that handle these gambits, we’ve created a Tic-Tac-Toe Grandmaster AI. It can’t be beaten, and guarantees that it will at least tie. Let’s review the new and improved rule set:
If the AI can win, do it; if the player can win, block it.
If the player moved first, and this is the AI’s first move, defend against the Center Square Gambit as follows:
Check to see if the player picked the center square.
If so, take a corner (it doesn’t matter which one); otherwise, continue processing rules.
If the player has moved twice (and the AI once) and the AI owns the center square, defend against the Corner Gambit as follows:
Check if the 1,4,7 column and the 3,4,5 row contain a single X, a single O, and an open space.
If so, put the AI token in any corner adjacent to a player token, or choose the AI move normally.
Check to see if the player owns cell 7 and either cell 0 or cell 2.
If so, put the AI’s token in the corner cell that is in the lower row and the same column as the X token in cell 0 or 2.
If the player has moved twice (and the AI once) and the player owns the center square, defend against the Sandbagging Gambit as follows:
Check to see if either diagonal (0,4,8 or 2,4,6) contains two player tokens and an AI token.
If so, put the AI token in the open upper corner, or choose the AI move normally.
If the player has moved three times (and the AI twice) and the AI owns the center square, do the following:
Check to see if there are two X tokens in adjacent non-corner squares.
If so, put an O token in the corner that is adjacent to both X tokens.
Apply the default algorithm like so:
If the center cell is open, take it.
If not, if a non-corner space is open, take it.
If not, if a corner is open, take it.
How could we implement these rules in code? I’m glad you asked. At this point, we need to crank up the XNA environment and get to work. I’m assuming you’ve either read through Appendix A and completed the coding work there or are familiar with XNA already and have reviewed the TicTacToeUI project found on the CD and understand my madness.
We will begin in a new XNA Windows Game 3.0 (or appropriate version) project named TicTacToeGM. First, import all the code and content from the
TicTacToeUI project (overwriting what is in the new project where necessary). See Figures 1.14 and 1.15 for a list of items that should be imported.
Note
The namespace I created in the TicTacToeUI project was simply TicTacToe despite the name of the project being different. This is fine in practice, but if you created your own version of the UI (in which case I owe you a Twinkie), and created a namespace that matched the project, you will want to update your namespace to match the new project.
Once your new project is created and you have imported the content from the TicTacToeUI project, run it, making sure there are no errors. It should look like what is shown in Figure 1.16.
Let’s begin by figuring out what changes we need to make to the base code in order to change it from a UI piece into a piece that can support playing a game of Tic-Tac-Toe. We need to add some members to the Game1 class to support gameplay. Specifically, we need to add game state variables to help the AI determine what is happening and when.
Open the Game1 class inside Game1.cs and find the member list. At the bottom of the list, add the following members:
//AI and game state variables
const int MAX_TURNS = 9;
int turn;
int moveAI;
int drawTurn;
bool AIWin;
bool playerWin;
//presentation variables
bool winMsgSent;
bool inPlay;
private Vector2 BoldBannerPos;The turn variable will be incremented to inform the AI of whose turn it is and when the game is a draw. It will also help the AI to know when to test against the special case we’ve identified above. Similarly, the drawTurn variable will inform the game when it should consider the game a draw. We use a variable to test against instead of the constant MAX_TURNS because to allow the AI to move first, it is just easier to increment the turn counter, which means the game would call a draw with one cell left open (we’ll talk more about this later). The bool state variables let the AI know if the AI won on the last round, or if the player won. Lastly, we’ve added a few presentation variables. These will help to keep the UI in good form.
Next, we need to initialize all the variables in the Initialize method. Find the method and, directly before the call to base.Initialize(), add the following:
//AI and game state variables intialization turn = 0; moveAI = -1; AIWin = false; playerWin = false; winMsgSent = false; inPlay = false; drawTurn = MAX_TURNS; //present position inits BoldBannerPos = new Vector2(25.0f, 5.0f);
Now we can look at implementing the AI algorithm listed above into the code base (we will address the copious amounts of changes to the Update method later). Luckily, this is a pretty simple set of tasks. Let’s start with a relatively easy task: figuring out if anyone has won the game.
For this task, we need to recall the heuristic we identified previously—specifically, that each token is assigned a value (including the space token) and that we are going to multiply these values instead of adding them. Given that, what are the termination conditions for the game?
Three X tokens in a row will have a total value of 3 * 3 * 3, or 27. Likewise, three O tokens in a row will have a total value of 5 * 5 * 5, or 125. We must check the value of any three-in-a-row token runs against these two values. Great! We can do this in a few seconds—we just need a routine that checks all the rows, all the columns, and both diagonals. To do so, consider the following code:
//a method to check all for a string of 3 tokens
private bool CheckWin(int p)
{
int testval = 0;
if (p = = 1)
{
//check to see if the player has won
testval = 27;
}
else
{
//check to see if the AI has won
testval = 125;
}
//check rows
for (int i = 0; i < 9; i += 3)
{
if (board[i].Value * board[i + 1].Value * board[i + 2].
Value = = testval)
{
screenText.Print("Three in a row! " + i + "," + (i + 1) + ","
+ (i + 2));
winMsgSent = true;
return true;
}
}
//check columns
for (int i = 0; i < 3; i++) {
if (board[i].Value * board[i + 3].Value * board[i + 6].
Value = = testval)
{
screenText.Print("Three in a row! " + i + "," + (i + 3) + ","
+ (i + 6));
winMsgSent = true;
return true;
}
}
//check the 0,4,8 diagonal
if (board[0].Value * board[4].Value * board[8].Value = = testval)
{
screenText.Print("Three in a row! 0,4,8");
winMsgSent = true;
return true;
}
//check the 2,4,6 diagonal
if (board[2].Value * board[4].Value * board[6].Value = = testval)
{
screenText.Print("Three in a row! 2,4,6");
winMsgSent = true;
return true;
}
return false;
}Nothing here is rocket science. First, we start by checking to see if we want to identify X token wins or O token wins. With that done, we can move on to testing the various three-in-a-rows—multiplying the values and comparing them with the correct termination value. If we find any rows that match the termination value, we add a message to the ScreenText class for presentation to the screen, we set a Boolean to help with the flow control of the game, and simply return true. The return value will be used to select different behaviors for the game in the Update method.
Well, that was certainly easy. The next method we need must identify the possibility of a win in the next move. The good news is that we can use CheckWin()as a “slightly more than” stub. Basically, we can use the same overall structure, and simply change what actions the code takes in response to the conditionals. Rather than dump another (and even larger) method on you in one chunk, let’s examine this in a piece-wise fashion. We will call the method IdentifyWin() and will take a single integer as a parameter. The method will return void and should have private security protection.
The first change to the code is in the testval values. Based on our established heuristic, we know that two X tokens plus a space should equal 3 * 3 * 2, or 18, while two O tokens in a row should total 5 * 5 * 2, or 50. Therefore, we just need to update the first conditional to look like this:
if (p = = 1)
{
//check for player potential win -- 3 * 3 * 2
testval = 18;
}
else
{
//check for AI potential win -- 5 * 5 * 2
testval = 50;
}Again, not rocket science. We also need to ensure that the class member moveAI has a value that does not map to an actual board position, so we simply set moveAI to −1 at the start of this method. Yes, if we have good technique and disciplined programming practices, that value should always be –1 as we hit this method, but, being human as we are (and addicted to Twinkies), there might be a special case in which that value is not reset. In other words, better safe than buggy.
The next big chunk is to identify possible wins in the rows. Again, we will use the same structure as the CheckWin() method and just replace the guts. Consider this code block:
//check rows
for (int i = 0; i < 9; i += 3)
{
if (board[i].Value * board[i + 1].Value * board[i + 2].Value = = testval)
{
if (board[i].Value = = 2)
{
// i is the open space, put the AI token here
moveAI = i;
return; }
else if (board[i + 1].Value = = 2)
{
// i+1 is the open space, put the AI token here
moveAI = i + 1;
return;
}
else
{
// i+2 is the open space, put the AI token here
moveAI = i + 2;
return;
}
}
}This code is fairly easy and self explanatory, but let’s take a moment to talk about how this IdentifyWin() method will be used. This method will be called as the first step of the AI as, according to our algorithm, the first step is to take a winning move or to block the opponent’s potentially winning move. You can see that we are hitting moveAI with the position in the two-token run that is occupied with a space.
We are going to do this same thing with the remaining chunks of code, starting with the check columns loop. This code should suffice:
//check columns
for (int i = 0; i < 3; i++)
{
if (board[i].Value * board[i + 3].Value * board[i + 6].Value = = testval)
{
if (board[i].Value = = 2)
{
// i is the open space, put the AI token here
moveAI = i;
return;
}
else if (board[i + 3].Value = = 2)
{
// i+3 is the open space, put the AI token here
moveAI = i + 3;
return;
} else
{
// i+6 is the open space, put the AI token here
moveAI = i + 6;
return;
}
}
}As you can see, we’ve done exactly the same thing here as we did with the check rows loop. Guess what? We’re going to do it again for both of the diagonals:
//check the 0,4,8 diagonal
if (board[0].Value * board[4].Value * board[8].Value = = testval)
{
if (board[0].Value = = 2)
{
// 0 is the open space, put the AI token here
moveAI = 0;
return;
}
else if (board[4].Value = = 2)
{
// 4 is the open space, put the AI token here
moveAI = 4;
return;
}
else
{
// 8 is the open space, put the AI token here
moveAI = 8;
return;
}
}
//check the 2,4,6 diagonal
if (board[2].Value * board[4].Value * board[6].Value = = testval)
{
if (board[2].Value = = 2)
{
// 2 is the open space, put the AI token here
moveAI = 2;
return; }
else if (board[4].Value = = 2)
{
// 4 is the open space, put the AI token here
moveAI = 4;
return;
}
else
{
// 6 is the open space, put the AI token here
moveAI = 6;
return;
}
}’Nuff said. Again, this is all pretty easy coding based on what we need and the identified heuristics. How much of the AI have we implemented at this point? Very little—certainly none of the difficult bits. If we do some straight math, we could say we’ve implemented at most 16.7 percent of the algorithm. Since I’ve already implemented the rest of the algorithm, I can say with some certainty that this was the easiest part and had the smallest cognitive load.
Well, Valued Reader, what are you waiting for? Let’s explore the balance of the AI in a chunk-wise manner (and note the catastrophic difference between chunk-wise and piece-wise). I’m a firm believer in scaffolding, so let’s start with the easy parts of the algorithm first. You’ve probably guessed that we need another method call, and you’re right. We need to create an aptly named method (oh, something like doAI) that takes no arguments, returns a void, and has a private security level. To do the easy bits, inside this method, we need to do a bunch of simple checks on board positions. Recall that our algorithm dictates the AI should always take the center position if it’s open, then choose any non-corner position, and finally choose between the remaining corner positions. This series of steps amounts to the default-case AI for our Tic-Tac-Toe Grandmaster AI.
In essence, the default-case AI is simple. Here’s the code:
//No one can win, no special case rules fired, apply the normal tic-tac-toe
algorithm
//take the open center
if (board[4].Value = = 2)
{
moveAI = 4;
return; }
//take any open non-corner
if ( board[1].Value = = 2 )
{
moveAI = 1;
return;
}
if (board[3].Value = = 2)
{
moveAI = 3;
return;
}
if (board[5].Value = = 2)
{
moveAI = 5;
return;
}
if (board[7].Value = = 2)
{
moveAI = 7;
return;
}
//take any open corner
if (board[0].Value = = 2)
{
moveAI = 0;
return;
}
if (board[2].Value = = 2)
{
moveAI = 2;
return;
}
if (board[6].Value = = 2)
{
moveAI = 6;
return;
}
if (board[8].Value = = 2)
{
moveAI = 8;
return;
}If you are going to hold a banana to my head and force me to further develop this AI, we need to start looking at the special-case processing. There are no grossly simpler chunks here; they are all about the same level of complexity. That being the case, let’s just take them in the order that they appear in the algorithm.
The first special case we need to address is the Center Square Gambit discussed previously. The implementation of this case is quite straightforward. We need to know which turn of the game we are in (which is part of the reason why we added the turn member to the class). The Center Square Gambit applies only if the player has moved and has taken the center square. This code solves this special case:
//there were no winning moves, so begin special case checking
if (turn = = 1)
{
//if we are in this method and turn = = 1, the player had the first move
//and we need to defend against the Center Square Gambit
if (board[4].Value = = 3)
{
//the player took the center square so block the Center Square Gambit
//by choosing a corner square instead of a non-corner square.
//since this is the second move of the game, all corners are open, so
//choose the upper left hand corner (position 0)
moveAI = 0;
return;
}
//if the player did not choose the center square, continue with the normal
//algorithm
}Again, there is nothing special in this code, right? This is a straightforward algorithm implementation.
The next two cases are time dependent in that both cases can be defended against in turn three. The first of these cases is the Corner Gambit. The defense against this gambit begins after the player has taken two moves and the AI has taken one. Further, this gambit relies on the AI having taken the center square as its move. Therefore, the next specification test in the implementation is a test to see if the AI owns the center square.
Let’s take a look at the code and discuss it from there:
else if (turn = = 3)
{
//if we are in this method and turn = = 3, the player has taken two moves,
//and the AI has taken 1. There are two gambits that may need to be
//defended against
//check to see if the AI owns the center square
if (board[4].Value = = 5)
{
//check to see if the 1,4,7 column and 3,4,5 row both contain
//a single X, a single 0, and a space, which is the test for
//the Corner Gambit
if ((board[1].Value * board[4].Value * board[7].Value = = 30) &&
(board[3].Value * board[4].Value * board[5].Value = = 30))
{
//defend against the gambit by picking a corner square adjacent to
//a player token
if (board[1].Value == 3)
{
//given the board layout, if we are here, we know position 0 is open
moveAI = 0;
return;
}
else if (board[7].Value = = 3)
{
//given the board layout, if we are here, we know position 8 is open
moveAI = 8;
return;
}
}As you can see, all we’ve done here is directly implement the algorithm we talked about earlier. We simply use the value system to determine if the 1,4,7 column and the 3,4,5 row are in the configuration required by the gambit. If so, we just need to decide whether to put the O token in cell 0 or cell 8, depending on which side of the board the gambit is running against. Easy peasy, right?
The next gambit we can defend against also relies on being in turn 3 and the AI owning the center square. In the Split Attack Gambit, the defense is slightly different, but also relies on picking the correct corner for the defense. Take a look at this code (keep in mind it is nested inside the preceding selection statement):
//else check for the Split Attack Gambit
else if (board[7].Value == 3)
{ if (board[0].Value = = 3)
{
moveAI = 6;
return;
}
else if (board[2].Value = = 3)
{
moveAI = 8;
return;
}
}
//else continue normal algorithmIn this case, we know the center square is owned by the AI. We test to see if cell 7 is owned by the player. (This is the only cell that can trigger this gambit due to how we coded the default selection cases.) If so, we test to see if the player also owns one of the two opposing corners (either cell 0 or cell 2) and choose the appropriate opposing corner for the AI to block this gambit.
In addition to those two cases, during turn 3, we can also defend against the Sandbagging Gambit, provided the player owns the center square. The following code extends the “if the AI owns the center square” selection statement.
//next check to see if the player owns the center
else if (board[4].Value = = 3)
{
//check for and defend against the Sandbagging Gambit
if (board[0].Value * board[4].Value * board[8].Value = = 45)
{
//to defend, choose the open upper corner
moveAI = 2;
return;
}
else if (board[2].Value * board[4].Value * board[6].Value = = 45)
{
//to defend, choose the open upper corner
moveAI = 0;
return;
}
//else continue the normal algorithm
}Again, in this case, we know the center square is owned by the AI. The Sandbagging Gambit relies on the player taking a non-productive corner square and ceding initiative to the AI. However, the gambit relies on the AI following the default algorithm, which would give initiative back to the player in the next round and setting up yet another of those dual three-in-a-row opportunities. To effectively block this gambit, all the AI needs to do is pick the open upper corner space, which will maintain initiative and ensure that the player can’t regain it.
The final gambit we need to defend against, the Misdirection Gambit, can be identified in turn 5. The first identifying characteristic we need to check is whether the AI owns the center square. If the player owns the center square, the player can’t implement the Misdirection Gambit, and we can move on to the default algorithm. If, however, the AI owns the center square, we need to check to see if the player owns two adjacent non-corner cells. If so, we need to pick the corner square between them. Take a look at the following code:
//check to see if we are in danger from the Misdirection Gambit
//check to see if the AI owns the center square
if (board[4].Value = = 5)
{
//if so, check to see if the player as two adjacent non-corner cells
if (board[1].Value = = 3 && board[3].Value = = 3 && board[0].Value = = 2)
{
//the player owns the top and left non-corner cells, pick cell 0 to block
moveAI = 0;
return;
}
else if (board[1].Value = = 3 && board[5].Value = = 3 && board[2].Value = = 2)
{
//the player owns the top and right non-corner cells, pick cell 2 to block
moveAI = 2;
return;
}
else if (board[7].Value = = 3 && board[5].Value = = 3 && board[8].Value = = 2)
{
//player owns the bottom and right non-corner cells, pick cell 8 to block
moveAI = 8;
return;
}
else if (board[3].Value = = 3 && board[7].Value = = 3 && board[6].Value = = 2)
{
//player owns the bottom and left non-corner cells, pick cell 6 to block
moveAI = 6; return;
}
}
//else proceed with regular algorithmAwesome! Guess what? We’re done with the AI! Wasn’t that easy?
What’s left? Well, we need to use all these nifty methods we just wrote. Specifically, we need to heavily modify the Update() function. The first thing we need to add is a check of the termination conditions. What are these conditions? We need to check to see if the player or the AI has already won the game.
This is fairly easy to accomplish given the CheckWin() method we just wrote. Let’s look at the following code:
//check to see if the player already won
if ( (! winMsgSent) && CheckWin(1))
{
playerWin = true;
winMsgSent = true;
screenText.Print("YOU WON!",
15000,
BoldBannerPos,
Color.Red,
ScreenText.FontName.ExclaimBold);
}
//check to see if the AI already won
if ( (!winMsgSent) && CheckWin(0))
{
AIWin = true;
winMsgSent = true;
screenText.Print("YOU LOST!",
15000,
BoldBannerPos,
Color.Red,
ScreenText.FontName.ExclaimBold);
}
//check for a draw
if ((!winMsgSent) && turn == drawTurn)
{
screenText.Print("DRAW!",
15000, BoldBannerPos,
Color.Red,
ScreenText.FontName.ExclaimBold);
//turn off the game
AIWin = playerWin = true;
winMsgSent = true;
screenText.Print("No more moves!");
}In these two conditional statements, we simply check to see if the player has won or the AI has won. We also check the Boolean we added called winMsgSent. With this Boolean, we are simply tracking whether we’ve already displayed a win message to the player. Since we set this variable only when the game has been won or tied, this check just helps us skip running the CheckWin() method unnecessarily. Keep in mind the architecture of this game. We run the Update() and Draw() methods regardless of whether we are actually playing a game of Tic-Tac-Toe at present, so we need these guards against game-time processing.
We also need to restructure some of the existing logic in the Update() method. For example, after we’ve checked the termination conditions, we need to do the following:
//update the input handler
input.Update(gameTime);
//update message handler
screenText.Update(gameTime);
//logic to control the background cell flashing after cell selection
if (isFlashing)
{
if (flashCnt >= NUM_FLASHES)
{
flashCnt = 0;
flashtTarget = -1;
isFlashing = false;
}
else
{
flashCnt++;
}
}Note that there is nothing new here; we’re just changing the order of execution a bit. We also need to add some functionality to the play button. What we want this button to do is give the player a way to let the AI move first. We also want the player to be able to start a new game anytime during an existing game, so we need to track whether the game has already started. We are going to do this with a Boolean called inPlay.
We want this functionality to run prior to the reset button logic, so we will move a few more lines of code and implement the play button like this:
//track the state of the buttons, changing textures as appropriate
if (input.PlayBtnDown())
{
//the play button is mid-click - change the texture to down
playBtn = playBtnDown;
}
else if (input.PlayBtnClicked())
{
//the play button just released - change the texture to up
playBtn = playBtnUp;
if (inPlay)
{
ResetBoard();
turn++;
drawTurn++;
inPlay = true;
}
else
{
//tell the AI to play first
if (turn == 0)
{
turn++;
drawTurn++;
inPlay = true;
}
}
}
if (input.ResetBtnDown())
{ //the reset button is mid-click - change the texture to down
resetBtn = resetBtnDown;
}
else if (input.ResetBtnClicked())
{
//the reset button just released - change the texture to up
resetBtn = resetBtnUp;
ResetBoard();
}You’ll see that we are doing something funky with turn counting. Simply put, when we want the AI to move first, we increment the turn counter. We have to do this to make it easy to determine whose turn it is. That way, we’ll know whether to process the inputs from the player or call the AI methods and let the AI move. Check out this code:
if (!AIWin && !playerWin)
{
//see whose turn it is
if (turn % 2 = = 1)
{
//if we are inside this code block, it is the AI's turn
doAI();
//doAI will pick an empty cell, so we don't need to check for emptiness
board[moveAI].TokenTexture = 0Tok;
board[moveAI].TokenColor = drawColor0;
board[moveAI].Value = 5;
flashtTarget = moveAI;
isFlashing = true;
turn++;
}
else
{
}Following this block of code, we’re just going to implement the input handling code. What we’re doing here, however, is first checking to see if we should do anything at all (in other words, if we have already won or lost). To determine whose turn it is, we simply take the modulo of turn and 2 (modulo is a fancy-schmancy math-geek way of saying “get the remainder from integer division”), checking to see if the value is equal to 1. If so, we do the AI, and make the AI move. If not, we process the player’s input like this:
//check for mouse clicks inside the board and add player tokens accordingly
if (input.MouseClicked() = = true)
{
//since typing 'x' is much shorter than 'input.Mouse.X'…
float x = input.Mouse.X;
float y = input.Mouse.Y;
//row and column flags
Boolean r0 = false;
Boolean r1 = false;
Boolean r2 = false;
Boolean c0 = false;
Boolean c1 = false;
Boolean c2 = false;
//cell target found by the row and column test
int cellTarget = -1;
//first find the column by comparing the mouse x to
the known cell limits
if (x >= 74)
{
if (x >= 122 && x <= 170)
{
c2 = true;
}
else
{
c1 = true;
}
}
else
{
c0 = true;
}
//then determine the row by a similar comparision
of mouse y
if (y >= 86)
{
if (y >= 134 && y <= 184)
{
r2 = true;
} else
{
r1 = true;
}
}
else
{
r0 = true;
}
//next, compare the r x c coordinates to find the
correct cell, and add the player token
//test the first row
if (r0)
{
//r0-c0 = cell 0
if (c0)
{
//check to see if the position is open
if (board[0].Value = = 2)
{
cellTarget = 0;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500);
return;
}
}
//r0-c1 = cell 1
if (c1)
{
//check to see if the position is open
if (board[1].Value = = 2)
{
cellTarget = 1;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500); return;
}
}
//r0-c2 = cell 2
if (c2)
{
//check to see if the position is open
if (board[2].Value = = 2)
{
cellTarget = 2;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500);
return;
}
}
}
//test the second row
if (r1)
{
//r1-c0 = cell 3
if (c0)
{
//check to see if the position is open
if (board[3].Value = = 2)
{
cellTarget = 3;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500);
return;
}
}
//r1-c1 = cell 4
if (c1)
{
//check to see if the position is open if (board[4].Value = = 2)
{
cellTarget = 4;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500);
return;
}
}
//r1-c2 = cell 5
if (c2)
{
//check to see if the position is open
if (board[5].Value = = 2)
{
cellTarget = 5;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500);
return;
}
}
}
//test the last row
if (r2)
{
//r2-c0 = cell 6
if (c0)
{
//check to see if the position is open
if (board[6].Value = = 2)
{
cellTarget = 6;
inPlay = true;
}
else {
screenText.Print("That space is taken!",
3500);
return;
}
}
//r2-c1 = cell 7
if (c1)
{
//check to see if the position is open
if (board[7].Value = = 2)
{
cellTarget = 7;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500);
return;
}
}
//r2-c2 = cell 8
if (c2)
{
//check to see if the position is open
if (board[8].Value = = 2)
{
cellTarget = 8;
inPlay = true;
}
else
{
screenText.Print("That space is taken!",
3500);
return;
}
}
}
if (cellTarget > -1 && board[cellTarget].isFree)
{
board[cellTarget].TokenTexture = XTok; board[cellTarget].TokenColor = drawColorX;
board[cellTarget].Value = 3;
flashtTarget = cellTarget;
isFlashing = true;
}
turn++;
}As you can see, not much has changed here. We add some logic to make sure the player is selecting an empty cell and, if not, provide some feedback and wait for a valid choice. Easy.
I’ve also made some changes to the ScreenText.cs file in order to allow the text in the text window to scroll. I’m not going to go through all the changes here, as they don’t really pertain to the AI, but will leave looking at the code as an exercise.
Yep. We did it, Valued Reader! We made an AI that can’t be beaten in the game of Tic-Tac-Toe. Of course, the AI doesn’t win much either, since it plays primarily to tie. It will, however, win if you let it. Actually, it may still be subject to some quirk of the game you forgot to mention to me when we were coding it, but I won’t hold it against you if it does. Honest. (Really, please do contact me if I’ve left a glaring 40-foot-wide hole here!)
That’s all well and good, but it’s time to cast a critical eye on this game and see what’s what. Here’s the first question: Is this game fun to play?
My answer: Not really.
Okay, okay, let’s ignore me for now and talk about you. In terms of game-playing AI, this game is pretty strong. Does the answer change if we look at it from the perspective of VGAI? You betcha—with a capital Betcha!
We discussed VGAI in terms of increasing believability, immersion, and engagement, and adding challenge to the gameplay. Let’s ignore the 800-lb. gorilla in the room and move right on to discussing “adding challenge to gameplay.” Does the AI in this example add challenge to gameplay? Yes. In fact, we could say it adds too much challenge to gameplay, since it can’t be beaten. Challenge is one thing; grinding away at the impenetrable wall of crushing defeat is another. Yes, AI can be too strong in video games and make the game frustrating to play—and that’s probably the case here.
Going back to the 800-lb. gorilla, does our AI increase believability, immersion, and engagement? In my honest opinion, no, it doesn’t. I definitely do not feel like I am playing an opponent; I’m merely beating my head against a bit of clever engineering.
Er … that’s bad, right? I mean, we set out some guidelines for what VGAI has to do and then blissfully ignored them. (I tried to warn you about me, Valued Reader.) But there is a silver lining here. We can fix both of the problems we’ve identified in our game. The first problem—that of making it beatable so we don’t just get frustrated—may appear to be easy; indeed, there are certainly some easy things that we may be able to do (like levels of difficulty á la Doom). Typically, however, this is a very hard problem, as I’ve already alluded to in the first few pages. If we make the AI mess up in too clunky a manner, players will believe the AI is dumb, and the game certainly won’t be very engaging and challenging. The second may appear to be extremely difficult, especially given that we are talking about a tic-tac-toe game here, but there is some low-hanging fruit in this space, and we can probably get a lot of mileage from some simple changes. The good news is that both problems are solvable, and we’re going to tackle them in Chapter 2.