3
Longest Common Subsequence Problems
Longest common subsequence (LCS) problems frequently arise in bio-informatics applications. The most general problem in this class is simply known as the LCS problem. However, this problem class comprises a whole range of specific problems that are mostly restricted cases of the general LCS problem. Apart from the general LCS problem, we will also deal with one specific restriction known as the repetition-free longest common subsequence (RFLCS) problem in this chapter. An important landmark in the development of metaheuristics for LCS problems was the application of beam search to the general LCS problem in 2009. This algorithm significantly outperformed any other algorithm that was known at that time. Most approaches proposed thereafter have been based on beam search.
In this chapter, we will describe the original beam search approach to the general LCS problem. Moreover, we describe Beam–ACO, which is one of the more recent proposals based on beam search. This algorithm is obtained by combining the metaheuristic ant colony optimization (ACO) with beam search. After presenting the adaptation of the Beam–ACO algorithm to solve the RFLCS problem, we will describe current state-of-the-art metaheuristic for the RFLCS problem. This algorithm is a (IPL) hybrid metaheuristics obtained by combining probabilistic solution construction with the application of an integer linear programming of solver for sub-instances of the original problems. The general idea of this approach has been outlined in section 1.2.7.
3.1. Introduction
The classical LCS problem and some well-known restricted cases, including the RFLCS problem, are technically described in the following, followed by a literature review and an outline of the organization of this chapter.
3.1.1. LCS problems
First of all we introduce the general LCS problem. (S, Σ) of the LCS problem consists of a set S = {s1, s2, …, sn} of n strings over a finite alphabet Σ. The problem consists of finding a longest string t∗ that is a subsequence of all the strings in S. Such a string t∗ is called the longest common subsequence of the strings in S. Note that string t is called a subsequence of string s if t can be produced from s by deleting characters. For example, dga is a subsequence of adagtta. As mentioned above, the problem has various applications in computational biology; see [SMI 81, JIA 02]. However, the problem has also been used in the context of more traditional computer science applications, such as data compression [STO 88], syntactic pattern recognition [LU 78], file comparison [AHO 83], text edition [SAN 83], query optimization in databases [SEL 88] and the production of circuits in field programmable gate arrays [BRI 04b].
The LCS problem was shown to be non-deteministic polynomial-time (NP)-hard [MAI 78] for an arbitrary number n of input strings. If n is fixed, the problem is polynomially solvable with dynamic programming [GUS 97]. Standard dynamic programming approaches for this problem require O(ln) of time and space, where l is the length of the longest input string and n is the number of strings. While several improvements may reduce the complexity of standard dynamic programming to O(ln−1) ([BER 00] provide numerous references), dynamic programming quickly becomes impractical when n grows. An alternative to dynamic programming was proposed by Hsu and Du [HSU 84]. This algorithm was further improved in [EAS 07, SIN 07] by incorporating branch and bound (B&B) techniques. The resulting algorithm, called specialized branching (SB), has a complexity of O(n|Σ||t∗|), where t∗ is the LCS. According to the empirical results given by Easton and Singireddy [EAS 08], SB outperforms dynamic programming for large n and small l. Additionally, Singireddy [SIN 07] proposed an integer programming approach based on branch and cut.
Approximate methods for the LCS problem were first proposed by Chin and Poon [CHI 94] and Jiang and Li [JIA 95]. The long run (LR) algorithm [JIA 95] returns the longest common subsequence consisting of a single letter, which is always within a factor of |Σ| of the optimal solution. The expansion algorithm (EXPANSION) proposed by Bonizzoni et al. [BON 01], and the Best-Next heuristic [FRA 95, HUA 04] also guarantee an approximation factor of |Σ|, however their results are typically much better than those of LR in terms of solution quality. Guenoche and Vitte [GUE 95] described a greedy algorithm that uses both forward and backward strategies and the resulting solutions are subsequently merged. Earlier approximate algorithms for the LCS problem can be found in Bergroth et al. [BER 98] and Brisk et al. [BRI 04b].
In 2007, Easton and Singireddy [EAS 08] proposed a large neighborhood search heuristic called time horizon specialized branching (THSB) that makes internal use of the SB algorithm. In addition, they implemented a variant of Guenoche and Vitte’s algorithm [GUE 95], referred to as G&V, that selects the best solution obtained from running the original algorithm with four different greedy functions proposed by Guenoche [GUE 04]. Easton and Singireddy [EAS 08] compared their algorithm with G&V, LR and EXPANSION, showing that THSB was able to obtain better results than all the competitors in terms of solution quality. Their results also showed that G&V outperforms EXPANSION and LR with respect to solution quality, while requiring less computation time than EXPANSION and a computation time comparable to LR. Finally, Shyu and Tsai [SHY 09] studied the application of ACO to the LCS problem and concluded that their algorithm dominates both EXPANSION and Best-Next in terms of solution quality, while being much faster than EXPANSION.
A break-through both in terms of computation time and solution quality was achieved with the beam search (BS) approach described by Blum et al. in [BLU 09]. BS is an incomplete tree search algorithm which requires a solution construction mechanism and bounding information. Blum et al. used the construction mechanism of the Best-Next heuristic that was mentioned above and a very simple upper bound function. Nevertheless, the proposed algorithm was able to outperform all existing algorithms at that time. Later, Mousavi and Tabataba [MOU 12b] proposed an extended version of this BS algorithm in which they use a different heuristic function and a different pruning mechanism. Another extension of the BS algorithm from [BLU 09] is the so-called Beam–ACO approach that was proposed in [BLU 10]. Beam–ACO is a hybrid metaheuristic that combines the algorithmic framework of ACO with a probabilistic, adaptive, solution construction mechanism based on BS. Finally, Lozano and Blum [LOZ 10] presented another hybrid metaheuristic approach which is based on variable neighborhood search (VNS). This technique applies an iterated greedy algorithm in the improvement phase and generates the starting solutions by invoking either BS or a greedy randomized procedure.
3.1.1.1. Restricted LCS problems
Apart from the general LCS as mentioned above, various restricted problems have been tackled in the literature. Some of these are described in the following. Others are mentioned in survey papers such as [BON 10].
3.1.1.2. Repetition-free longest common subsequence
The repetition-free longest common sequence (RFLCS) problem is defined with two input strings s1 and s2 over a finite alphabet Σ. The goal is to find a longest common subsequence of s1 and s2 with the additional restriction that no letter may appear more than once in any valid solution. This problem was introduced in [ADI 08, ADI 10] as a comparison measure for two sequences of biological origin. In the same paper(s), the authors proposed three heuristics for solving this problem.
Three metaheuristic approaches were described in the literature for solving the RFLCS problem. The first one was the adaptation of the Beam–ACO algorithm [BLU 09] from the LCS problem to the RFLCS problem; see [BLU 14b]. A metaheuristic – particularly a genetic algorithm – specifically designed for the RFLCS problem can be found in [CAS 13]. Finally, the current state-of-the-art method is a construct, merge, solve and adapt (CMSA) approach that was presented by Blum and Blesa in [BLU 16a]. This last approach generates, at each iteration, sub-instances of the original problems and solves these by means of an integer linear programming (ILP) solver.
Bonizzoni et al. [BON 07] studied some variants of the RFLCS, such as the one in which some symbols are required to appear in the solution sought possibly more than once. They showed that these variants are approximable (APX)-hard and that, in some cases, the problem of deciding the feasibility of an instance is NP-complete.
3.1.1.3. Constrained longest common subsequence
The constrained longest common subsequence (C-LCS) problem was introduced in [TSA 03] for the case in which a longest common subsequence must be found for two input strings s1 and s2 over alphabet Σ that have a known common substructure. More specifically, given two input strings s1 and s2 and a third string sc, the C-LCS seeks the longest common subsequence of s1 and s2 that is also a supersequence of sc. Note that for this particular problem variant, polynomial time algorithms exist [TSA 03, CHI 04]. However, when the problem is generalized to a set of input strings, or to a set of constraint strings, the problem is NP-hard [GOT 08]. A dynamic programming algorithm for the problem is presented in [ZHU 15].
3.1.1.4. Generalized constrained longest common subsequence
This problem was tackled in [CHE 11b]. Given two input strings s1 and s2 over an alphabet Σ, and a third string t (called the pattern), the task is to find the longest common subsequence of s1 and s2 that includes (or excludes) t as a subsequence (or as a substring). The authors propose dynamic programming algorithms for solving the GC-LCS problem in O(nmr), where n is the length of s1, m the length of s2, and r the length of t.
3.1.2. ILP models for LCS and RFLCS problems
The LCS problem can be stated in terms of an integer linear program in the following way. Let us denote the length of any input string si by |si|. The positions in string si are numbered from 1 to |si|. The letter at position j of si is denoted by si[j]. The set Z of binary variables that is required for the ILP model is composed as follows. For each combination of indices 1 ≤ ki ≤ |si| for all i = 1, … , n such that s1[k1] = … = sn[kn], set Z contains a binary variable zk1,…,kn. Consider, as an example, instance I := (S = {s1, s2, s3}, Σ = {a, b, c, d}), where s1 = dbcadcc, s2 = acabadd and s3 = bacdcdd. In this case set Z would consist of 22 binary variables: three variables concerning letter a (z4,1,2, z4,3,2 and z4,5,2), one variable concerning letter b (z2,4,1), six variables concerning letter c (such as z3,2,3 and z6,2,5) and 12 variables concerning letter d (such as z1,6,4 and z5,7,4). Moreover, we say that two variables ![]() are in conflict, if and only if two indices exist
are in conflict, if and only if two indices exist ![]() such that ki ≤ li and kj ≥ lj. Concerning the problem mentioned above, variable pairs (z4,1,2, z4,3,2) and (z4,5,2, z3,2,3), are in conflict, whereas variable pair (z4,1,2, z6,2,5) is not in conflict. The LCS problem can then be rephrased as the problem of selecting the maximum number of non-conflicting variables from Z. With these notations, the ILP for the LCS problem is stated as follows:
such that ki ≤ li and kj ≥ lj. Concerning the problem mentioned above, variable pairs (z4,1,2, z4,3,2) and (z4,5,2, z3,2,3), are in conflict, whereas variable pair (z4,1,2, z6,2,5) is not in conflict. The LCS problem can then be rephrased as the problem of selecting the maximum number of non-conflicting variables from Z. With these notations, the ILP for the LCS problem is stated as follows:
subject to:
Therefore, constraints [3.2] ensure that selected variables are not in conflict.
In the case of the RFLCS problem, one set of constraints has to be added to the ILP model outlined above in order to ensure that a solution contains each letter from Σ a maximum of once. In this context, let Za ⊂ Z denote the subset of Z that contains all variables zk1,k2 such that s1[k1] = s2[k2] = a, for all a ∈ Σ1. The ILP model for the RFLCS problem is then stated as follows:
subject to:
3.1.3. Organization of this chapter
This chapter is organized as follows. Section 3.2 presents the original BS algorithm for the LCS problem. Moreover, a Beam–ACO metaheuristic is described. This section concludes with an experimental evaluation of both algorithms on a benchmark set for the LCS problem. Algorithms for the RFLCS problem are outlined in section 3.3. We will describe CMSA, which is the current state-of-the-art technique for the RFLCS problem. This section concludes with an experimental evaluation. Finally, the chapter ends with conclusions and some interesting future lines of research.
3.2. Algorithms for the LCS problem
3.2.1. Beam search
BS is an incomplete derivative of B&B that was introduced in [RUB 77]. In the following sections, we will describe the specific variant of BS (from [BLU 09]) that was used to solve the LCS problem. The central idea behind BS is to allow the extension of partial solutions in several possible ways. In each step, the algorithm chooses at most |μkbw| feasible extensions of the partial solutions stored in a set B, which is called the beam. Therefore, kbw is the beam width that serves as an upper limit for the number of partial solutions in B and μ ≥ 1 is a parameter of the algorithm. Feasible extensions are chosen in a deterministic way by means of a greedy function that gives a weight to each feasible extension. At the end of each step, a new beam B is obtained by selecting up to kbw partial solutions from the set of chosen feasible extensions. For this purpose, BS algorithms calculate – in the case of maximization – an upper bound value for each chosen extension. Only the maximally kbw best extensions – with respect to the upper bound – are added to the new B set. Finally, the best complete solution generated in this way is returned.
BS has been applied in quite a number of research papers in recent decades. Examples include scheduling problems [OW 88, SAB 99, GHI 05], berth allocation [WAN 07], assembly line balancing [ERE 05] and circular packing [AKE 09]. Crucial components of BS are: (1) the constructive heuristic that defines the feasible extensions of partial solutions; (2) the upper bound function for evaluating partial solutions. The application of BS to the LCS problem is described by focusing on these two crucial components.
3.2.1.1. Constructive heuristic
BEST-NEXT [FRA 95, HUA 04] is a fast heuristic for the LCS problem. It produces a common subsequence t from left to right, adding exactly one letter from Σ to the current subsequence at each construction step. The algorithm stops when no further letters can be added without producing an invalid solution. The pseudo-code is provided in Algorithm 3.1.
Algorithm 3.1. BEST-NEXT heuristic for the LCS problem

For a detailed technical description of how BEST-NEXT works, let us consider problem I = (S = {s1, s2, s3}, Σ = {a, b, c, d}), where s1 = dbcadcc, s2 = acabadd and s3 = bacdcdd. Given a partial solution t to problem (S, Σ), BEST-NEXT makes use of the following:
- 1) given a partial solution t, each input string si can be split into substrings xi and yi, i.e. si = xi · yi, such that t is a subsequence of xi and yi is of maximum length;
- 2) given a partial solution t, for each si ∈ S we introduce a position pointer pi := |xi|, i.e. pi points to the last character in xi, assuming that the first character of a string has position one. The partition of input strings si into substrings as well as the corresponding position pointers are shown with respect to example I and the partial solution t = ba in Figure 3.1;
- 3) the position in which a letter first appears a ∈ Σ in a string si ∈ S after the position pointer pi is well-defined and denoted by
 . When letter a ∈ Σ does not appear in
. When letter a ∈ Σ does not appear in  is set to ∞. This is also shown in Figure 3.1;
is set to ∞. This is also shown in Figure 3.1;
4) letter a ∈ Σ is dominated if there is at least one letter b ∈ Σ, a ≠ b, such that ![]() for i = 1, … , n. Consider, for example, partial solution t = b in the context of example I. In this case, a dominates d, as letter a always appears before letter d in yi (∀ i ∈ {1, 2, 3});
for i = 1, … , n. Consider, for example, partial solution t = b in the context of example I. In this case, a dominates d, as letter a always appears before letter d in yi (∀ i ∈ {1, 2, 3});
5) ![]() denotes the set of non-dominated letters with respect to partial solution t. Obviously letter
denotes the set of non-dominated letters with respect to partial solution t. Obviously letter ![]() appears in each string si at least once after the position pointer pi.
appears in each string si at least once after the position pointer pi.

Figure 3.1. Consider example I := (S = {s1, s2, s3}, Σ = {a, b, c, d}), where s1 = dbcadcc, s2 = acabadd, and s3 = bacdcdd. Let t = ba be the current partial solution. Figures a), b), and c) show the separation of si into xi and yi. In addition, position pointers pi and the next positions of the four letters in yi are indicated. If, for some i, yi does not contain a specific letter, the corresponding pointer is set to ∞. This happens, for example, in the case of letters a and b in  and
and 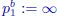
In Function Choose_From![]() – see line 4 of Algorithm 3.1 – exactly one letter is chosen from
– see line 4 of Algorithm 3.1 – exactly one letter is chosen from ![]() at each iteration. Subsequently, the chosen letter is appended to t. The choice of a letter is made by means of a greedy function. We then present the greedy function (labeled
at each iteration. Subsequently, the chosen letter is appended to t. The choice of a letter is made by means of a greedy function. We then present the greedy function (labeled ![]() that works well in the context of the problems considered in this chapter:
that works well in the context of the problems considered in this chapter:

This greedy function calculates the average length of the remaining parts of all strings after the next occurrence of letter a after the position pointer. Function Choose_From![]() chooses
chooses ![]() such that η(a|t) ≥ η(b|t) for all
such that η(a|t) ≥ η(b|t) for all ![]() . In the case of ties, the lexicographically smallest letter is taken.
. In the case of ties, the lexicographically smallest letter is taken.
3.2.2. Upper bound
In addition to the mechanism for extending partial solutions based on a greedy function, the second crucial aspect of BS is the upper bound function for evaluating partial solutions. Remember that any common subsequence t splits each string si ∈ S into a first part xi and a second part yi, i.e. si = xi ·yi. In this context, let |yi|a denote the number of occurrences of letter a ∈ Σ in yi. The upper bound value of t is then defined as follows:
This upper bound is obtained by totalling a ∈ Σ the minimum number (over i = 1, … , n) of occurrences of each letter in yi and adding the resulting sum to the length of t. Consider, as an example, partial solution t = ba concerning the problems shown in Figure 3.1. As letters a, b and c do not occur in the remaining part of input string s2, they do not contribute to the upper bound value. Letter d appears at least once in each yi (∀ i ∈ {1, 2, 3}). Therefore, the upper bound value of ba is |ba| + 1 = 2 + 1 = 3.
Finally, note that this upper bound function can be computed efficiently by keeping appropriate data structures. Even though the resulting upper bound values are not very tight, experimental results have shown that it is capable of guiding the search process of BS effectively.
3.2.3. Beam search framework
The BS algorithm framework for the LCS problem, which is pseudo-coded in Algorithm 3.2, works roughly as follows. Apart from problem (S, Σ), the algorithm asks for values for two input parameters: (1) the beam width (kbw ∈ ![]() ; and (2) a parameter used to determine the number of extensions that can be chosen in each step (μ ∈
; and (2) a parameter used to determine the number of extensions that can be chosen in each step (μ ∈ ![]() ≥ 1). In each step of the algorithm, there is also a set B of subsequences called the beam. At the start of the algorithm, B contains only the empty string denoted by
≥ 1). In each step of the algorithm, there is also a set B of subsequences called the beam. At the start of the algorithm, B contains only the empty string denoted by ![]() , i.e. B := {
, i.e. B := {![]() }. Let EB denote the set of all possible extensions of the partial solutions – i.e. common subsequences – from B. In this context, remember that a subsequence t is extended by appending exactly one letter from
}. Let EB denote the set of all possible extensions of the partial solutions – i.e. common subsequences – from B. In this context, remember that a subsequence t is extended by appending exactly one letter from ![]() . At each step, the best |μkbw| extensions from EB are selected with respect to the greedy function η(.|.). When a chosen extension is a complete solution, it is stored in set Bcompl. When it is not, it is added to the beam of the next step. However, this is only done when its upper bound value, UB(), is greater than the length of the best solution so far tbsf. At the end of each step, the new beam B is reduced (if necessary) to kbw partial solutions. This is done by evaluating the subsequences in B by means of the upper bound function UB() and by selecting the kbw subsequences with the greatest upper bound values.
. At each step, the best |μkbw| extensions from EB are selected with respect to the greedy function η(.|.). When a chosen extension is a complete solution, it is stored in set Bcompl. When it is not, it is added to the beam of the next step. However, this is only done when its upper bound value, UB(), is greater than the length of the best solution so far tbsf. At the end of each step, the new beam B is reduced (if necessary) to kbw partial solutions. This is done by evaluating the subsequences in B by means of the upper bound function UB() and by selecting the kbw subsequences with the greatest upper bound values.
Algorithm 3.2. BS for the LCS problem

The BS algorithm for the LCS problem uses four different functions. Given the current beam B as input, function Produce_Extensions(B) generates the set EB of non-dominated extensions of all the subsequences in B. More specifically, EB is a set of subsequences ta, where t ∈ B and ![]() .
.
The second function, Filter_Extensions(EB), weeds out the dominated extensions from EB. This is done by extending the non-domination relation that was defined in section 3.2.1.1 for two different extensions of one specific subsequence to the extensions of different subsequences of the same length. Formally, given two extensions ta, zb ∈ EB, where t ≠ z but not necessarily a ≠ b, ta dominates zb if and only if the position pointers concerning a appear before the position pointers concerning b in the corresponding remaining parts of the n strings.
The third function, Choose_Best_Extension(EB), is used to choose extensions from EB. Note that for the comparison of two extensions ta and zb from EB, the greedy function is only useful where t = z, while it might be misleading where t ≠ z. This problem is solved as follows. First, the weights assigned by the greedy function are replaced with the corresponding ranks. More specifically, given all extensions ![]() of a subsequence t, the extension tb with η(b|t) ≥ η(a|t) for all
of a subsequence t, the extension tb with η(b|t) ≥ η(a|t) for all ![]() receives rank 1, denoted by r(b|t) = 1. The extension with the second highest greedy weight receives rank 2, etc. The evaluation of an extension ta is then made on the basis of the sum of the ranks of the greedy weights that correspond to the steps performed to construct subsequence ta, i.e.
receives rank 1, denoted by r(b|t) = 1. The extension with the second highest greedy weight receives rank 2, etc. The evaluation of an extension ta is then made on the basis of the sum of the ranks of the greedy weights that correspond to the steps performed to construct subsequence ta, i.e.

where t[1…i] is the prefix of t from position 1 to position i and t[i] the letter at position i of string t. Note that, in contrast to the greedy function weights, these newly defined ν() values can be used to compare extensions of different subsequences. In fact, a call of function Choose_ Best_Extension(EB) returns the extension from EB with maximum ν()−1 value.
Finally, the last function used within the BS algorithm is Reduce(B, kbw). Where |B| > kbw, this function removes from B step-by-step those subsequences t that have an upper bound value UB(t) smaller or equal to the upper bound value of that are the other subsequences in B. The removal process stops once |B| = kbw.
3.2.4. Beam–ACO
Beam–ACO, which is a general hybrid metaheuristic that was first introduced in [BLU 05], works roughly as follows. At each iteration, a probabilistic BS algorithm is applied, based both on greedy/pheromone information and on bounding information. The solutions constructed are used to update the pheromone values. In other words, the algorithmic framework of Beam–ACO is that of ACO; see section 1.2.1 for an introduction to ACO. However, instead of performing a number of sequential and independent solution constructions per iteration, a probabilistic BS algorithm is applied.
3.2.4.1. Pheromone model
One of the most important aspects of any ACO algorithm is the pheromone model, ![]() . In the case of the LCS problem, coming up with a pheromone model is not immediately intuitive. In [BLU 10], the authors finally defined a pheromone model,
. In the case of the LCS problem, coming up with a pheromone model is not immediately intuitive. In [BLU 10], the authors finally defined a pheromone model, ![]() , that for each position j of a string si ∈ S contains a pheromone value 0 ≤ τij ≤ 1, i.e.
, that for each position j of a string si ∈ S contains a pheromone value 0 ≤ τij ≤ 1, i.e. ![]() = {τij | i = 1, … , n, j = 1, … , |si|}. Note that τij ∈
= {τij | i = 1, … , n, j = 1, … , |si|}. Note that τij ∈ ![]() represents the benefit of adding the letter at position j in the string si to the solution under construction: the greater τij, the greater the aim of adding the corresponding letter. Based on this pheromone model, solutions in Beam–ACO – henceforth called ACO-solutions – can be represented in a specific way. Note that any common subsequence t of the strings in S – that is, any solution t – can be translated into a unique ACO-solution T = {Tij ∈ {0, 1} | i = 1, … , n, j = 1, … , |si|} in a well-defined way which works as follows: for each string si ∈ S the positions of the letters of t in si are determined in such a way that each letter is in the farthest left position possible. These positions j are set to 1 in T – that is, Tij = 1 – and Tij = 0 otherwise. For example, consider S = {dbcadcc, acabadd, bacdcdd} from Figure 3.1 and a possible solution t = bad. This solution translates into the ACO-solution T = {0101100, 0001110, 1101000}.
represents the benefit of adding the letter at position j in the string si to the solution under construction: the greater τij, the greater the aim of adding the corresponding letter. Based on this pheromone model, solutions in Beam–ACO – henceforth called ACO-solutions – can be represented in a specific way. Note that any common subsequence t of the strings in S – that is, any solution t – can be translated into a unique ACO-solution T = {Tij ∈ {0, 1} | i = 1, … , n, j = 1, … , |si|} in a well-defined way which works as follows: for each string si ∈ S the positions of the letters of t in si are determined in such a way that each letter is in the farthest left position possible. These positions j are set to 1 in T – that is, Tij = 1 – and Tij = 0 otherwise. For example, consider S = {dbcadcc, acabadd, bacdcdd} from Figure 3.1 and a possible solution t = bad. This solution translates into the ACO-solution T = {0101100, 0001110, 1101000}.
3.2.4.2. Algorithm framework
In the following we outline the Beam–ACO approach for the LCS problem which was originally proposed in [BLU 10]. This Beam–ACO approach is based on a standard min-max ant system (MMAS) implemented in the hyper-cube framework (HCF); see [BLU 04]. The algorithm is pseudo-coded in Algorithm 3.3. The data structures of this algorithm are: (1) the best solution so far Tbs, i.e. the best solution generated since the start of the algorithm; (2) the restart-best solution Trb, i.e. the best solution generated since the last restart of the algorithm; (3) the convergence factor cf, 0 ≤ cf ≤ 1, which is a measure of the state of convergence of the algorithm; (4) the Boolean variable bs_update, which assumes the value TRUE when the algorithm reaches convergence.
Algorithm 3.3. Beam–ACO for the LCS problem

After the initialization of the pheromone values to 0.5, each iteration consists of the following steps. First, the BS from section 3.2.1 is applied in a probabilistic way, guided by greedy information and pheromone values. This results in a solution, Tpbs. Second, the pheromone update is conducted in function ApplyPheromoneUpdate(cf, bs_update, ![]() , Tpbs, Trb, Tbs). Third, a new value for the convergence factor cf is computed. Depending on this value, as well as on the value of the Boolean variable bs_update, a decision on whether or not to restart the algorithm is made. If the algorithm is restarted, all the pheromone values are reset to their initial value (i.e. 0.5). The algorithm is iterated until a maximum computation time limit is reached. Once terminated, the algorithm returns the string version tbs of the best-so-far ACO-solution Tbs, the best solution found. We will describe the two remaining procedures in Algorithm 3.3 in more detail:
, Tpbs, Trb, Tbs). Third, a new value for the convergence factor cf is computed. Depending on this value, as well as on the value of the Boolean variable bs_update, a decision on whether or not to restart the algorithm is made. If the algorithm is restarted, all the pheromone values are reset to their initial value (i.e. 0.5). The algorithm is iterated until a maximum computation time limit is reached. Once terminated, the algorithm returns the string version tbs of the best-so-far ACO-solution Tbs, the best solution found. We will describe the two remaining procedures in Algorithm 3.3 in more detail:
– ApplyPheromoneUpdate(cf,bs_update,![]() ,Tpbs,Trb,Tbs): as usual in MMAS algorithms implemented in the HCF, three solutions are used update pheromone values. These are solution Tpbs generated by BS, the restart-best solution Trb and the best solution so far Tbs. The influence of each solution on pheromone update depends on the state of convergence of the algorithm, as measured by the convergence factor cf. Each pheromone value τij ∈
,Tpbs,Trb,Tbs): as usual in MMAS algorithms implemented in the HCF, three solutions are used update pheromone values. These are solution Tpbs generated by BS, the restart-best solution Trb and the best solution so far Tbs. The influence of each solution on pheromone update depends on the state of convergence of the algorithm, as measured by the convergence factor cf. Each pheromone value τij ∈ ![]() is updated as follows:
is updated as follows:
where:
where κpbs is the weight (i.e. the influence) of solution Tpbs, κrb is the weight of solution Trb, κbs is the weight of solution Tbs and κpbs + κrb + κbs = 1. After the pheromone update rule (equation [3.11]) is applied, pheromone values that exceed τmax = 0.999 are set back to τmax and those pheromone values that fall below τmin = 0.001 are set back to τmin. This is done in order to avoid a complete convergence of the algorithm, which is a situation that should be avoided. Equation [3.12] allows us to choose how to weight the relative influence of the three solutions used for updating the pheromone values. For application to the LCS problem, a standard update schedule as shown in Table 3.1 was used.
– ComputeConvergenceFactor(![]() ): the convergence factor cf, which is a function of the current pheromone values, is computed as follows:
): the convergence factor cf, which is a function of the current pheromone values, is computed as follows:

Note that when the algorithm is initialized (or reset) it holds that cf = 0. When the algorithm has converged, then cf = 1. In all other cases, cf has a value in (0, 1). This completes the description of the learning component of our Beam–ACO approach for the LCS problem.
Table 3.1. Setting of κpbs, κrb, κbs, and ρ depending on the convergence factor cf and the Boolean control variable bs_update

Finally, we will describe the way in which BS is made probabilistic on the basis of the pheromone values. Function Choose_Best_Extension(EB) in line 8 of Algorithm 3.2 is replaced by a function that chooses an extension ta ∈ EB (where t is the current partial solution and a is the letter appended to produce extension ta) based on the following probabilities:

Remember in this context, that ![]() was defined as the next position of letter a after position pointer pi in string si. The intuition of choosing the minimum pheromone values corresponding to the next positions of a letter in the n given strings is as follows: if at least one of these pheromone values is low, the corresponding letter should not yet be appended to the partial solution because there is another letter that should be appended first. Finally, each application of the probabilistic choice function is either executed probabilistically or deterministically. This is decided with uniform probability. In the case of a deterministic choice, we simply choose the extension with the highest probability value. The probability for a deterministic choice, also called the determinism rate, is henceforth denoted by drate ∈ [0, 1].
was defined as the next position of letter a after position pointer pi in string si. The intuition of choosing the minimum pheromone values corresponding to the next positions of a letter in the n given strings is as follows: if at least one of these pheromone values is low, the corresponding letter should not yet be appended to the partial solution because there is another letter that should be appended first. Finally, each application of the probabilistic choice function is either executed probabilistically or deterministically. This is decided with uniform probability. In the case of a deterministic choice, we simply choose the extension with the highest probability value. The probability for a deterministic choice, also called the determinism rate, is henceforth denoted by drate ∈ [0, 1].
3.2.5. Experimental evaluation
The three algorithms outlined in the previous sections – henceforth labeled Best-Next, BS and Beam–ACO – were implemented in ANSI C++ using GCC 4.7.3, without the use of any external libraries. Note that – in the case of the LCS problem – it is not feasible to solve the ILP models corresponding to the problems considered (see section 3.1.2) by means of an ILP solver such as CPLEX. The number of variables is simply too high. The experimental evaluation was performed on a cluster of PCs with Intel(R) Xeon(R) CPU 5670 CPUs of 12 nuclei of 2933 MHz and at least 40 GB of RAM. Initially, the set of benchmarks that were generated to compare the three algorithms considered are described. Then, the tuning experiments that were performed in order to determine a proper setting for the Beam–ACO parameters are outlined. Note that in the case of BS, a low time and a high time configuration, as in [BLU 09], was chosen manually. Finally, an exhaustive experimental evaluation is also presented.
3.2.5.1. Problems
Most algorithmic proposals for the LCS problem from the literature were evaluated using randomly-generated problems. This was also done for the experimental evaluation of Best-Next, BS and Beam–ACO. As many as 10 random instances were generated for each combination of the number of input strings n ∈ {10, 50, 100, 150, 200}, the length of the input stings m ∈ {100, 500, 1000} and the alphabet size |Σ| ∈ {4, 12, 20}. This makes a total of 450 problems. All the results shown in forthcoming sections are averages over the 10 problems of each combination.
3.2.5.2. Tuning
The parameters involved in Beam–ACO – apart from the learning rate ρ which is not critical and which was set as shown in Table 3.1 – are basically those involved in the probabilistic beam search that is employed at each iteration: (1) the beam width (kbw); (2) the parameter that controls the number of extensions that are chosen at each step of beam search (μ); and (3) the determinism rate (drate).
The automatic configuration irace tool [LÓP 11] was used for tuning the three parameters. In fact, irace was applied to tune Beam–ACO separately for each combination of input strings (n) and alphabet size (|Σ|). In preliminary experiments the length of the input strings did not seem to have a major influence on the performance of the algorithm. For each combination of n, |Σ| and m, three tuning instances were randomly generated. This results in nine tuning instances per application of irace.
Each application of irace was given a budget of 1,000 runs of Beam–ACO, where each run was given a computation time limit of ![]() CPU seconds. Finally, the following parameter value ranges were chosen concerning the three parameters considered for tuning:
CPU seconds. Finally, the following parameter value ranges were chosen concerning the three parameters considered for tuning:
- – kbw ∈ {5, 10, 30, 50, 100};
- – μ ∈ {1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0};
- – drate ∈ {0.0, 0.3, 0.6, 0.9}, where a value of 0.0 means that the choice of an extension is made uniformly at random with respect to their probabilities, while a value of 0.9 means that BS is nearly deterministic, in the sense that the extension with the highest probability is nearly always chosen deterministically.
The tuning runs with irace produced the configurations of Beam–ACO as shown in Table 3.2.
3.2.5.3. Experimental results
Four algorithms were included in the comparison. Apart from the Best-Next heuristic and Beam–ACO, BS was applied with two different parameter settings. The first setting, henceforth referred to as the low time setting, is characterized by kbw = 10 and μ = 3.0. The corresponding algorithm version is called BS-L. The second setting, which we refer to as the high quality setting, assumes kbw = 100 and μ = 5.0. This version of BS is referred to as BS-H. Additional experiments have shown that an additional increase in performance by increasing the value of any of these two parameters is rather minor and on the cost of much higher running times. Just like in the tuning phase, the maximum CPU time given to Beam–ACO for the application to each problem was ![]() CPU seconds.
CPU seconds.
Table 3.2. Results of tuning Beam–ACO with irace

The numerical results are presented in Tables 3.3, 3.4 and 3.5 in terms of one table per alphabet size. Each row presents the results averaged over 10 problems of the same type. The results of all algorithms are provided in two columns. The first one (mean) provides the result of the corresponding algorithm averaged over 10 problems, while the second column (time) provides the average computation time (in seconds) necessary to find the corresponding solutions. The best result for each row is marked with a gray background.
The following observations can be made:
- – first of all, both BS variants – i.e. BS-L and BS-H – and Beam–ACO clearly outperform Best-Next. Moreover, the high-performance version of BS outperforms the low time version;
- – for alphabet size |Σ| = 4 – particularly for larger instances – Beam–ACO seems to outperform the other algorithms. However, starting from an alphabet size of |Σ| = 12, BS-H has advantages over Beam–ACO;
- – BS-H requires computation times that are comparable with those of Beam–ACO.
Table 3.3. Results for instances where |Σ| = 4

Table 3.4. Results for instances where |Σ| = 12

Table 3.5. Results for instances where |Σ| = 20

Finally, the results are also presented in graphical form in terms of the improvement of Beam–ACO over the other three algorithms in Figures 3.2, 3.3 and 3.4. The labels on the x-axis indicate the number and length of the input strings of the corresponding instances. More specifically, a label is of the form X-Y, where X is the number of input strings and Y indicates their length.
3.3. Algorithms for the RFLCS problem
We will now present the best available algorithms for the RFLCS problem. The first one is a simple adaption of the Beam–ACO algorithm presented in section 3.2.4 for the general LCS problem. In fact, the extension to the RFLCS problem only concerns function Produce_ Extensions(B) and the calculation of the upper bound function (UB(·)) in Algorithm 3.2. Remember that function Produce_Extensions(B) produces the set EB of all extensions of the common subsequences t ∈ B, where B is the current beam. More specifically, EB is the set of subsequences ta, where t ∈ B and ![]() . To adopt this function to the RFLCS problem, all letters that appear in a common subsequence t ∈ B must be excluded from
. To adopt this function to the RFLCS problem, all letters that appear in a common subsequence t ∈ B must be excluded from ![]() . Additionally, the upper bound function must be adapted. For any common subsequence t, the upper bound value in the context of the RFLCS problem is defined as follows:
. Additionally, the upper bound function must be adapted. For any common subsequence t, the upper bound value in the context of the RFLCS problem is defined as follows:


Figure 3.2. Improvement of Beam–ACO over Best-Next. Each box shows the differences between the objective function value of the solution produced by Beam–ACO and the one of the solution produced by Best-Next for the 10 instances of the same type

Figure 3.3. Improvement of Beam–ACO over BS-L. Each box shows the differences between the objective function value of the solution produced by Beam–ACO and the one of the solution produced by BS-L for the 10 instances of the same type

Figure 3.4. Improvement of Beam–ACO over BS-H. Each box shows the differences between the objective function value of the solution produced by Beam–ACO and the one of the solution produced by BS-H for the 10 instances of the same type
In addition to the Beam–ACO approach, the current state-of-the-art approach is outlined in the subsequent section.
3.3.1. CMSA
The application of the construct, merge, solve and adapt (CMSA) algorithm to the RFLCS problem was originally described in [BLU 16a]. As already described in section 1.2.7, the CMSA approach works as follows. At each iteration, solutions to the problem tackled are generated in a probabilistic way. The components found in these solutions are, then, added to a sub-instance of the original problem. Subsequently, an exact solver such as, for example, CPLEX is used to optimally solve the sub-instance. Moreover, the algorithm is equipped with a mechanism for deleting seemingly useless components from the sub-instance. This is done such that the sub-instance has a moderate size and can be solved quickly.
The pseudo-code of CMSA for the RFLCS problem is given in Algorithm 3.4. Note that in the context of this algorithm, solutions to the problem and sub-instances are both subsets of the complete set Z of variables that was described in section 3.1.2. If a solution S contains a variable zk1, k2, the variable assumes a value of one in the corresponding solution.
CMSA starts by setting the best solution so far Sbsf to NULL and the restricted problem (Zsub) to the empty set. The CMSA main loop is executed before the CPU time limit is reached. It consists of the following actions. First, a number of na solutions is probabilistically constructed in function ProbabilisticSolutionConstruction(Z) in line 6 of Algorithm 3.4. The variables that are found in these solutions are added to Zsub. The age of a newly added variable zk1, k2 (age[zk1, k2]) is set to 0. After the construction of na solutions, an ILP solver is applied to find the best solution ![]() in the sub-instance Zsub (see function ApplyILPSolver(Zsub) in line 12 of Algorithm 3.4.). Where
in the sub-instance Zsub (see function ApplyILPSolver(Zsub) in line 12 of Algorithm 3.4.). Where ![]() is better than the current best solution so far Sbsf, solution
is better than the current best solution so far Sbsf, solution ![]() is stored as the new best solution so far (line 13). Next, sub-instance Zsub is adapted, based on solution
is stored as the new best solution so far (line 13). Next, sub-instance Zsub is adapted, based on solution ![]() and on the age of the variables. This is done in function Adapt(
and on the age of the variables. This is done in function Adapt(![]() ) in line 14 as follows. First, the age of each variable in Zsub is increased by one and, subsequently, the age of each variable in
) in line 14 as follows. First, the age of each variable in Zsub is increased by one and, subsequently, the age of each variable in ![]() is re-set to zero. Finally, those solution components from Zsub that have reached the maximum component age (agemax) are deleted from Zsub. The motivation behind the aging mechanism is that variables which never appear in an optimal solution of Zsub should be removed from Zsub after a while, because they simply slow down the ILP solver. Components which appear in optimal solutions seem to be useful and should, therefore, remain in Zsub.
is re-set to zero. Finally, those solution components from Zsub that have reached the maximum component age (agemax) are deleted from Zsub. The motivation behind the aging mechanism is that variables which never appear in an optimal solution of Zsub should be removed from Zsub after a while, because they simply slow down the ILP solver. Components which appear in optimal solutions seem to be useful and should, therefore, remain in Zsub.
The ILP solver used in function ApplyILPSolver(Zsub) makes use of the ILP model for the RFLCS problem outlined in section 3.1.2. In order to apply this model to a sub-instance, Zsub, all occurrences of Z in this model have to be replaced with Zsub.
The remaining component in the application of CMSA to the RFLCS problem is the probabilistic construction of solutions in function ProbabilisticSolutionConstruction(Z). For this purpose, CMSA uses a probabilistic version of the Best-Next heuristic that was described in section 3.2.1.1 for the more general LCS problem. The probabilistic heuristic is described in terms of the variables used in the context of CMSA. The solution starts with an empty partial solution ![]() . The first action at each step consists of generating the set C of variables that serve as options to be added to S. C is generated in order to contain for each letter a ∈ Σ, for which S does not yet contain a corresponding variable, the variable zk1, k2 ∈ Za (if any) so that k1 < l1 and
. The first action at each step consists of generating the set C of variables that serve as options to be added to S. C is generated in order to contain for each letter a ∈ Σ, for which S does not yet contain a corresponding variable, the variable zk1, k2 ∈ Za (if any) so that k1 < l1 and ![]() . Assuming that zr1, r2 was the last variable added to S, all options zk1, k2 ∈ C are assigned a weight value
. Assuming that zr1, r2 was the last variable added to S, all options zk1, k2 ∈ C are assigned a weight value ![]() . Only when
. Only when ![]() , does r1 = r2 = 0. Note that these weight values correspond exactly to the weight values assigned by greedy function η() from section 3.2.1.1. At each step, exactly one variable is chosen from C and added to S. First, a value δ is chosen uniformly at random from [0, 1]. In the case δ ≤ drate, where drate is a parameter of the algorithm, the variable zi,j ∈ C with the greatest weight is deterministically chosen. Otherwise, a candidate list L ⊆ C of size min{lsize, |C|} containing the options with the highest weight is generated and exactly one variable zi,j ∈ L is then chosen uniformly at random and added to S. Note that lsize is another parameter of the solution construction process. The construction of a complete (valid) solution is finished when the set of options is empty.
, does r1 = r2 = 0. Note that these weight values correspond exactly to the weight values assigned by greedy function η() from section 3.2.1.1. At each step, exactly one variable is chosen from C and added to S. First, a value δ is chosen uniformly at random from [0, 1]. In the case δ ≤ drate, where drate is a parameter of the algorithm, the variable zi,j ∈ C with the greatest weight is deterministically chosen. Otherwise, a candidate list L ⊆ C of size min{lsize, |C|} containing the options with the highest weight is generated and exactly one variable zi,j ∈ L is then chosen uniformly at random and added to S. Note that lsize is another parameter of the solution construction process. The construction of a complete (valid) solution is finished when the set of options is empty.
Algorithm 3.4. CMSA for the RFLCS problem

3.3.2. Experimental evaluation
We implemented both algorithms outlined earlier – henceforth labeled Beam–ACO and CMSA – in ANSI C++ using GCC 4.7.3, without the use of any external libraries. The ILP models of the original RFLCS and the sub-instances within CMSA, were solved with IBM ILOG CPLEX v12.2 in one-threaded mode. The experimental evaluation was performed on a cluster of PCs with Intel(R) Xeon(R) CPU 5670 CPUs of 12 nuclei of 2933 MHz and at least 40 GB of RAM. Initially, the set of benchmarks used to test the algorithms considered are described. Then, the tuning experiments performed in order to determine a proper setting for the algorithm parameters are outlined. Finally, an exhaustive experimental evaluation is presented.
3.3.2.1. Problems
Two different types of problems are proposed in the related literature (see [ADI 08, ADI 10]) for testing algorithms for the RFLCS problem. For the experimental evaluation of this chapter we chose type one instances. More specifically, the instances used in the following are generated on the basis of alphabet sizes |Σ| ∈ {32, 64, 128, 256, 512} and the maximum repetition of each letter rep ∈ {3, 4, 5, 6, 7, 8} in each input string. For each combination of |Σ| and rep the instance set considered consists of 10 randomly generated problems, which makes a total of 300 problems. All the results shown in the forthcoming sections are averages over the 10 problems of each type.
3.3.2.2. Tuning of Beam–ACO
Remember that, the parameters involved in Beam–ACO – apart from the learning rate ρ which is not that critical and which was set to 0.1 – are basically those involved in the probabilistic BS that is employed at each iteration: (1) the beam width (kbw); (2) the parameter that controls the number of extensions that are chosen at each step of beam search (μ); (3) the determinism rate (drate).
The automatic configuration tool irace [LÓP 11] was used for the tuning of the three parameters. In fact, irace was applied to tune Beam–ACO separately for instances concerning a specific alphabet size (|Σ|). This is because – as in the case of the LCS problem; see section 3.2.5.2 – the length of the input strings did not seem to have a major influence on the performance of the algorithm. For each combination of |Σ| and rep, two tuning instances are randomly generated. This results in 12 tuning instances per application of irace.
Table 3.6. Results of Beam–ACO tuning for the RFLCS problem with irace

Table 3.7. Results of CMSA tuning for the RFLCS problem with irace

Each application of irace was given a budget of 1000 runs of Beam–ACO, where each run was given a computation time limit of ![]() CPU seconds. The parameter value ranges for the three parameters considered were chosen as in the case of the LCS problem; see section 3.2.5.2. The tuning runs with irace produced the Beam–ACO configurations shown in Table 3.6.
CPU seconds. The parameter value ranges for the three parameters considered were chosen as in the case of the LCS problem; see section 3.2.5.2. The tuning runs with irace produced the Beam–ACO configurations shown in Table 3.6.
3.3.2.3. Tuning CMSA
There are several parameters involved in CMSA: (na) the number of solution constructions per iteration, (agemax) the maximum allowed age of solution components, (drate) the determinism rate, (lsize) the candidate list size and (tmax) the maximum time in seconds allowed for CPLEX per application to a sub-instance. The last parameter is necessary, because even when applied to reduced problems, CPLEX might still need too much computation time for optimal sub-instance solutions. In any case, CPLEX always returns the best feasible solution found within the given computation time.
As in the case of Beam–ACO, we made use of the automatic configuration tool irace [LÓP 11] to tune the five parameters. Again, irace was applied to tune CMSA separately for each alphabet size. The tuning instances were the same as the ones used to tune Beam–ACO. The tuning process for each alphabet size was given a budget of 1000 runs of CMSA, where each run was given a computation time limit of ![]() CPU seconds. Finally, the following parameter value ranges were chosen concerning the five parameters of CMSA:
CPU seconds. Finally, the following parameter value ranges were chosen concerning the five parameters of CMSA:
- – na ∈ {10, 30, 50};
- – agemax ∈ {1, 5, 10, inf}, where inf means that solution components are never removed from the incumbent sub-instance;
- – drate ∈ {0.0, 0.3, 0.5, 0.7, 0.9}, where a value of 0.0 means that the selection of the component to be added to the partial solution under construction is always selected randomly from the candidate list, while a value of 0.9 means that solution constructions are nearly deterministic;
- – lsize ∈ {3, 5, 10};
- – tmax ∈ {0.5, 1.0, 5.0} (in seconds) for instances where |Σ| ∈ {32, 64} and tmax ∈ {1.0, 10.0, 100.0} for instances where |Σ| > 64.
Tuning with irace produced the CMSA configurations shown in Table 3.7.
3.3.2.4. Experimental results
Three solution techniques were included in the comparison. Apart from Beam–ACO and CMSA, CPLEX was additionally applied to all problems. In contrast to the LCS problem, this is feasible in the case of the RFLCS problem, at least for smaller problems. Just like in the tuning phase, the maximum CPU time given to all algorithms for the application to each problem was ![]() CPU seconds.
CPU seconds.
The numerical results are presented in Table 3.8. Each row presents the results averaged over 10 problems of the same type. The results of Beam–ACO and CMSA are provided in two columns. The first one (mean) provides the result of the corresponding algorithm averaged over 10 problems, while the second column (time) provides the average computation time (in seconds) necessary to find the corresponding solutions. The same information is given for CPLEX. However in this case we will also provide the average optimality gaps (in percent), i.e. the average gaps between the upper bounds and the values of the best solutions when stopping a run.
Table 3.8. Experimental results concerning the RFLCS problem

The following observations can be made:
- – CPLEX is able to solve all instances where |Σ| = 32 and reps < 8 to optimality. Moreover, CPLEX is able to provide valid – although sometimes far from optimal – solutions up to instances where |Σ| = 256 and reps ≤ 4; with the exception of instances where |Σ| = 128 and reps = 8;
- – CMSA is the best-performing algorithm for instances where |Σ| ≤ 256. Curiously, the performance of CMSA seems to degrade with growing alphabet size. More specifically, Beam–ACO outperforms CMSA for instances where |Σ| = 512. Moreover, the computation time required by Beam–ACO for doing so is almost negligible.
Finally, the results are also presented in graphical form in terms of the improvement of CMSA over the other two techniques in Figures 3.5 and 3.6. The labels of the x-axes of these figures provide information on the reps parameter of the corresponding instances. Note that when a box shows negative values – i.e. negative improvements – the competitor algorithm was better than CMSA.

Figure 3.5. Improvement of CMSA over Beam–ACO. Each box shows the differences between the objective function value of the solution produced by CMSA and the one of the solution produced by Beam–ACO for 10 instances of the same type

Figure 3.6. Improvement of CMSA over CPLEX. Each box shows the differences between the objective function value of the solution produced by CMSA and that of the solution produced by CPLEX for 10 instances of the same type. Missing boxes indicate that CPLEX was not able to produce any valid solution
3.4. Future work
In this chapter, after giving an introduction to the family of longest common subsequence problems, the current state-of-the-art metaheuristics for two specific longest common subsequence problems were presented. The first one was the most general LCS problem and the second one the RFLCS problem. The general impression is that the high-performance version of BS is a very strong algorithm for the LCS problem and that it will be difficult to significantly outperform this algorithm by means of some pure metaheuristic framework.
The situation for the RFLCS problem is a bit different. Although the CMSA algorithm works very well and better than Beam–ACO, in the context of small and medium size problems, the performance of CMSA seems to degrade with growing alphabet size. An interesting line for future research would be the combination of both techniques, i.e. using the Beam–ACO algorithm (or a simpler BS algorithm) to feed the sub-instance in the context of CMSA with new solution components. In other words, it might be beneficial to replace the simply probabilistic construction mechanism of CMSA with probabilistic BS or Beam–ACO.
