2 Functions

Chapter Outline

2.1 Functions and Graphs

2.2 Symmetry and Transformations

2.3 Linear Functions

2.4 Quadratic Functions

2.5 Piecewise-Defined Functions

2.6 Combining Functions

2.7 Inverse Functions

2.8 Building a Function from Words

2.9 The Tangent Line Problem

      Chapter 2 Review Exercises

2.1 Functions and Graphs

Introduction Using the objects and the persons around us, it is easy to make up a rule of correspondence that associates, or pairs, the members, or elements, of one set with the members of another set. For example, to each social security number there is a person, to each car registered in the state of California there is a license plate number, to each book there corresponds at least one author, to each state there is a governor, and so on. A natural correspondence occurs between a set of 20 students and a set of, say, 25 desks in a classroom when each student selects and sits in a different desk. In mathematics we are interested in a special type of correspondence, a single-valued correspondence, called a function.

In the student/desk correspondence above suppose the set of 20 students is the set X and the set of 25 desks is the set Y. This correspondence is a function from the set X to the set Y provided no student sits in two desks at the same time.

Terminology A function is usually denoted by a letter such as f, g, or h. We can then represent a function f from a set X to a set Y by the notation f:X → Y. The set X is called the domain of f. The set of corresponding elements y in the set Y is called the range of the function. For our student/desk function, the set of students is the domain and the set of 20 desks actually occupied by the students constitutes the range. Notice that the range of f need not be the entire set Y. The unique element y in the range that corresponds to a selected element x in the domain X is called the value of the function at x, or the image of x, and is written f(x). The latter symbol is read “f of x” or “f at x”, and we write y = f(x).* See FIGURE 2.1.1. Since the value of y depends on the choice of x, y is called the dependent variable; x is called the independent variable. Unless otherwise stated, we will assume hereafter that the sets X and Y consist of real numbers.

FIGURE 2.1.1 Domain and range of a function f

Student-desk correspondence

EXAMPLE 1 The Squaring Function

The rule for squaring a real number is given by the equation y = x²or f(x) = x². The values of f at x = −5 and are obtained by replacing x, in turn, by the numbers −5 and :

Occasionally for emphasis we will write a function using parentheses in place of the symbol x. For example, we can write the squaring function f(x) = x² as

This illustrates the fact that x is a placeholder for any number in the domain of the function y = f(x). Thus, if we wish to evaluate (1) at, say, 3 + h, where h represents a real number, we put 3 + h into the parentheses and carry out the appropriate algebra:

If a function f is defined by means of a formula or an equation, then typically the domain of y = f(x) is not expressly stated. We will see that we can usually deduce the domain of y = f(x) either from the structure of the equation or from the context of the problem.

See (6) of Section 1.5.

EXAMPLE 2 Domain and Range

In Example 1, since any real number x can be squared and the result x² is another real number, f(x) = x² is a function from R to R, that is, f:R → R. In other words, the domain of f is the set R of real numbers. Using interval notation, we also write the domain as (−∞, ∞). The range of f is the set of nonnegative real numbers or [0, ∞); this follows from the fact that x² ≥ 0 for every real number x.

Domain of a Function As mentioned earlier, the domain of a function y = f(x) that is defined by a formula is usually not specified. Unless stated or implied to the contrary, it is understood that:

The domain of a function f is the largest subset of the set of real numbers for which f(x) is a real number.

This set is sometimes referred to as the implicit domain of the function. For example, we cannot compute f(0) for the reciprocal function f(x) = 1/x since 1/0 is not a real number. In this case we say that f is undefined at x = 0. Since every nonzero real number has a reciprocal, the domain of f(x) = 1/x is the set of real numbers except 0. By the same reasoning, the function g(x) = 1/(x² − 4) is not defined at either x = −2 or x = 2, and so its domain is the set of real numbers with −2 and 2 excluded. The square root function is not defined at x = −1 because is not a real number. In order for to be defined in the real number system we must require the radicand, in this case simply x, to be nonnegative. From the inequality x ≥ 0 we see that the domain of the function h is the interval [0, ∞).

EXAMPLE 3 Domain and Range

Determine the domain and range of .

Solution The radicand x − 3 must be nonnegative. By solving the inequality x − 3 ≥ 0 we get x ≥ 3, and so the domain of f is [3, ∞). Now, since the symbol denotes the nonnegative square root of a number, for x ≥ 3 and consequently . The smallest value of f(x) occurs at x = 3 and is . Moreover, because x − 3 and increase as x takes on increasing larger values, we conclude that y ≥ 4. Consequently the range of f is [4, ∞).

EXAMPLE 4 Domain of f

Determine the domain of .

Solution As in Example 3, the expression under the radical symbol—the radicand—must be nonnegative, that is, the domain of f is the set of real numbers x for which x² + 2x - 15 ≥ 0 or (x − 3)(x + 5) ≥ 0. We have already solved the last inequality by means of a sign chart in Example 3 of Section 1.1. The solution set of the inequality (−∞, −5] ∪ [3, 8) is also the domain of f.

EXAMPLE 5 Domains of Two Functions

Determine the domain of the given function.

(a) and (b)

Solution A function that is given by a fractional expression is not defined at the x-values for which its denominator is equal to 0.

(a) The expression under the radical is the same as in Example 4. Since x² + 2x − 15 is in the denominator we must have x² + 2x − 15 ≠ 0. This excludes x = −5 and x = 3. In addition, since x² + 2x − 15 appears under a radical, we must have x² + 2x − 15 > 0 for all other values of x. Thus the domain of the function g is the union of two open intervals (−∞, −5) ∪ (3, ∞).

(b) Since the denominator of h(x) factors,

we see that (x + 1)(x − 4) = 0 for x = −1and x = 4. In contrast to the function in part (a), these are the only numbers for which h is not defined. Hence, the domain of the function h is the set of real numbers with x = −1 and x = 4 excluded.

Using interval notation, the domain of h in part (b) of Example 5 can be written as

As an alternative to this ungainly union of disjoint intervals, this domain can also be written using set-builder notation as {x | x ≠ −1 and x ≠ 4}.

Graphs A function is often used to describe phenomena in fields such as science, engineering, and business. In order to interpret and utilize data, it is useful to display this data in the form of a graph. The graph of a function f is the graph of the set of ordered pairs (x, f(x)), where x is in the domain of f. In the xy-plane an ordered pair (x, f(x)) is a point, so that the graph of a function is a set of points. If a function is defined by an equation y = f(x), then the graph of f is the graph of the equation. To obtain points on the graph of an equation y = f(x), we judiciously choose numbers x₁, x₂, x₃,… in its domain, compute f(x₁), f(x₂), f(x₃),…, plot the corresponding points (x₁, f(x₁)), (x₂, f(x₂)), (x₃, f(x₃)),…, and then connect these points with a curve. See FIGURE 2.1.2. Keep in mind that:

• a value of x is a directed distance from the y-axis, and
• a function value f(x) is a directed distance from the x-axis.

FIGURE 2.1.2 Points on the graph of an equation y = f(x)

A word about the figures in this text is in order. With a few exceptions, it is usually impossible to display the complete graph of a function, and so we often display only the more important features of the graph. In Figure 2.1.3(a), notice that the graph goes down on its left and right sides. Unless indicated to the contrary, we may assume that there are no major surprises beyond what we have shown and the graph simply continues in the manner indicated. The graph in Figure 2.1.3(a) indicates the so-called end behavior or global behavior of the function: for a point (x, y) on the graph, y → − ∞ as x → − ∞ and y→ − ∞ as x → ∞. (More will be said about this concept of global behavior in Chapter 3.) If a graph terminates at either its right or left end, we will indicate this by a dot when clarity demands it. See Figure 2.1.4. We will use a solid dot to represent the fact that the end point is included on the graph and an open dot to signify that the end point is not included on the graph.

Vertical Line Test From the definition of a function we know that for each x in the domain of f there corresponds only one value f(x) in the range. This means a vertical line that intersects the graph of a function y = f(x) (this is equivalent to choosing an x) can do so in at most one point. Conversely, if every vertical line that intersects a graph of an equation does so in at most one point, then the graph is the graph of a function. The last statement is called the vertical line test for a function. See FIGURE 2.1.3(a). On the other hand, if some vertical line intersects a graph of an equation more than once, then the graph is not that of a function. See Figures 2.1.3(b) and 2.1.3(c). When a vertical line intersects a graph in several points, the same number x corresponds to different values of y in contradiction to the definition of a function.

FIGURE 2.1.3 Vertical line test

If you have an accurate graph of a function y = f(x) it is often possible to see the domain and range of f. In FIGURE 2.1.4 assume that the colored curve is the entire, or complete, graph of some function f. The domain of f then is the interval [a, b] on the x-axis and the range is the interval [c, d] on the y-axis.

FIGURE 2.1.4 Domain and range interpreted graphically

EXAMPLE 6 Example 3 Revisited

From the graph of given in FIGURE 2.1.5, we can see that the domain and range of f are, respectively, [3, ∞) and [4, ∞). This agrees with the results in Example 3.

As shown in Figure 2.1.3(b), a circle is not the graph of a function. Actually, an equation such as x² + y² = 9 defines (at least) two functions of x. If we solve this equation for y in terms of x we get . Because of the single-valued convention of the sign, both equations define functions. As we saw in Section 1.4, the first equation defines an upper semicircle and the second defines a lower semicircle. From the graphs shown in FIGURE 2.1.6, the domain of is [−3, 3] on the x-axis and the range is [0, 3] on the y-axis; the domain and range of are [−3, 3] and [−3, 0], respectively.

FIGURE 2.1.5 Graph of function f in Example 6

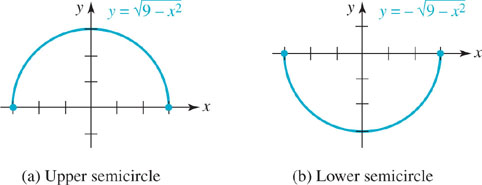
FIGURE 2.1.6 These semicircles are graphs of functions

Intercepts To graph a function defined by an equation y = f(x), it is usually a good idea to first determine whether the graph of f has any intercepts. Recall that all points on the y-axis are of the form (0, y). Thus, if 0 is the domain of a function f, the y-intercept is the point on the y-axis whose y-coordinate is f(0), in other words, (0, f(0)). See FIGURE 2.1.7(a). Similarly, all points on the x-axis have the form (x, 0).This means that to find the x-intercepts of the graph of y = f(x), we determine the values of x that make y = 0. That is, we must solve the equation f(x) = 0 for x. A number c for which

is referred to as either a zero of the function f or a root (or solution) of the equation f(x) = 0. The real zeros of a function f are the x-coordinates of the x-intercepts of the graph of f. In Figure 2.1.7(b), we have illustrated a function that has three zeros x₁, x₂, and x₃ because f(x₁) = 0, f(x₂) = 0, and f(x₃) = 0. The corresponding three x-intercepts are the points (x₁, 0), (x₂, 0), and (x₃, 0). Of course, the graph of the function may have no intercepts. This is illustrated in Figure 2.1.5.

FIGURE 2.1.7 Intercepts of the graph of a function f

A graph does not necessarily have to cross a coordinate axis at an intercept; a graph could simply be tangent to, or touch, an axis. In Figure 2.1.7(c) the graph of y = f(x) is tangent to the x-axis at (x₁, 0). Also, the graph of a function f can have at most one y-intercept since, if 0 is the domain of f, there can correspond only one y-value, namely, y = f(0).

More will be said about this in Chapter 3.

EXAMPLE 7 Intercepts

Find, if possible, the x- and y-intercepts of the given function.

(a) f(x) = x² + 2x − 2

(b)

Solution

(a) Since 0 is in the domain of f, f(0) = −2 is the y-coordinate of the y-intercept of the graph of f. The y-intercept is the point (0,–2). To obtain the x-intercepts we must determine whether f has any real zeros, that is, real solutions of the equation f(x) = 0. Since the left-hand side of the equation x² + 2x − 2 = 0 has no obvious factors, we use the quadratic formula to obtain . Since the zeros of f are the numbers . The x-intercepts are the points and .

(b) Because 0 is not in the domain of f (f(0) = −3/0 is not defined), the graph of f possesses no y-intercept. Now since f is a fractional expression, the only way we can have f(x) = 0 is to have the numerator equal zero. Factoring the left-hand side of x² − 2x − 3 = 0 gives (x + 1) (x − 3) = 0. Therefore the numbers −1 and 3 are the zeros of f. The x-intercepts are the points (−1, 0) and (3, 0).

Approximating Zeros Even when it is obvious that the graph of a function y = f(x) possesses x-intercepts it is not always a straightforward matter to solve the equation f(x) = 0. In fact, it is impossible to solve some equations exactly; some times the best we can do is to approximate the zeros of the function. One way of doing this is to obtain a very accurate graph of f.

EXAMPLE 8 Approximate Intercepts

With the aid of a graphing utility the graph of the function f(x) = x³ − x + 4 is given in FIGURE 2.1.8. From f(0) = 4 we see that the y-intercept is (0, 4). As we see in the figure, there appears to be only one x-intercept with x-coordinate close to − 1.7 or − 1.8. But there is no convenient way of finding the roots of the equation x³ − x + 4 = 0.We can however approximate the real root of this equation with the aid of the, find root feature of either a graphing calculator or computer algebra system. We find that x ≈ − 1.796 and so the approximate x-intercept is (−1.796, 0). As a check, note that the function value

FIGURE 2.1.8 Approximate x-intercept in Example 8

is nearly 0.

NOTES FROM THE CLASSROOM

When sketching the graph of a function, you should never resort to plotting a lot of points by hand. That is something a graphing calculator or a computer algebra system (CAS) does so well. On the other hand, you should not become dependent on a calculator to obtain a graph. Believe it or not, there are precalculus and calculus instructors who do not allow the use of graphing calculators on quizzes or tests. Usually there is no objection to your using calculators or computers as an aid in checking homework problems, but in the classroom instructors want to see the product of your own mind, namely, the ability to analyze. So you are strongly encouraged to develop your graphing skills to the point where you are able to quickly sketch by hand the graph of a function from a basic familiarity of types of functions and by plotting a minimum of well-chosen points.

2.1 Exercises
Answers to selected odd-numbered problems begin on page ANS–3.

In Problems 1–6, find the indicated function values.

1.

2.

3.

4.

5.

6.

In Problems 7 and 8, find

for the given function f and simplify as much as possible.

7. f( ) = −2( )² + 3( )

8. f( ) = ( )³ − 2( )² + 20

9. For what values of x is f(x) = 6x² − 1 equal to 23?

10. For what values of x is equal to 4?

In Problems 11–20, find the domain of the given function f.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

In Problems 21–26, use the sign-chart method to find the domain of the given function f.

21.

22.

23.

24.

25.

26.

In Problems 27–30, determine whether the graph in the figure is the graph of a function.

27.

FIGURE 2.1.9 Graph for Problem 27

28.

FIGURE 2.1.10 Graph for Problem 28

29.

FIGURE 2.1.11 Graph for Problem 29

30.

FIGURE 2.1.12 Graph for Problem 30

In Problems 31–34, use the graph of the function f given in the figure to find its domain and range.

31.

FIGURE 2.1.13 Graph for Problem 31

32.

FIGURE 2.1.14 Graph for Problem 32

33.

FIGURE 2.1.15 Graph for Problem 33

34.

FIGURE 2.1.16 Graph for Problem 34

In Problems 35–42, find the zeros of the given function f.

35. f(x) = 5x + 6

36. f(x) = −2x + 9

37. f(x) = x² − 5x + 6

38. f(x) = x² − 2x − 1

39. f(x) = x(3x − 1)(x + 9)

40. f(x) = x³ − x² − 2x

41. f(x) = x⁴ − 1

42.

In Problems 43–50, find the x- and y-intercepts, if any, of the graph of the given function f. Do not graph.

43.

44. f(x) = x² − 6x + 5

45. f(x) = 4(x − 2)² − 1

46. f(x) = (2x − 3)(x² + 8x + 16)

47.

48.

49.

50.

In Problems 51 and 52, find two functions y = f₁(x) and y = f₂(x) defined by the given equation. Find the domain of the functions f₁ and f₂.

51. x = y² − 5

52. x² − 4y² = 16

In Problems 53 and 54, use the graph of the function f given in the figure to estimate the values of f(−3), f(−2), f(−1), f(1), f(2), and f(3). Estimate the y-intercept.

53.

FIGURE 2.1.17 Graph for Problem 53

54.

FIGURE 2.1.18 Graph for Problem 54

In Problems 55 and 56, use the graph of the function f given in the figure to estimate the values of f(−2), f(−1.5), f(0.5), f(1), f(2), and f(3.2). Estimate the x-intercepts.

55.

FIGURE 2.1.19 Graph for Problem 55

56.

FIGURE 2.1.20 Graph for Problem 56

Miscellaneous Calculus-Related Problems

57. In calculus some of the functions that you will encounter have as their domain the set of positive integers n. The factorial function f(n) = n! is defined as the product of the first n positive integers, that is,

(a) Evaluate f(2), f(3), f(5), and f(7).

(b) Show that f(n + 1) = f(n) • (n + 1).

(c) Simplify f(n + 2)/f(n).

58. Another function of a positive integer n gives the sum of the first n squared positive integers:

(a) Find the value of the sum 1² + 2² + ⋯ + 99²+ 100².

(b) Find n such that 300 < S(n) < 400. [Hint: Use a calculator.]

For Discussion

59. Determine an equation of a function y = f(x) whose domain is (a) [3, ∞), (b) (3, ∞).

60. Determine an equation of a function y = f(x) whose range is (a) [3, ∞), (b) (3, ∞).

2.2 Symmetry and Transformations

Introduction In this section we discuss two aids in sketching graphs of functions quickly and accurately. If you determine in advance that the graph of a function possesses symmetry, then you can cut your work in half. In addition, sketching a graph of a complicated-looking function is expedited if you recognize that the required graph is actually a transformation of the graph of a simpler function. This latter graphing aid is based on your prior knowledge of the graphs of some basic functions.

FIGURE 2.2.1 Brief catalogue of power functions f(x) = xⁿ for various n

Power Functions A function of the form

where n represents a real number, is called a power function. The domain of a power function depends on the power n. For example, we have already seen in Section 2.1 for n = 2, , and n = −1, respectively, that:

• the domain of f(x) = x² is the set R of real numbers or (− ∞, ∞),
• the domain of is [0, ∞),
• the domain of is the set R of real numbers except x = 0.

Simple power functions, or modified versions of these functions, occur so often in problems in calculus that you do not want to spend valuable time plotting their graphs. We suggest that you know (memorize) the short catalogue of graphs of power functions given in FIGURE 2.2.1 on the previous page. You might already know that the graph in part (a) of that figure is a line and the graph in part (b) is called a parabola.

Symmetry In Section 1.4 we discussed symmetry of a graph with respect to the y-axis, the x-axis, and the origin. Of those three types of symmetries, the graph of a function can be symmetric with respect to the y-axis or with respect to the origin, but the graph of a nonzero function cannot be symmetric with respect to the x-axis. See Problem 43 in Exercises 2.2. If the graph of a function is symmetric with respect to the y-axis, we say that f is an even function. A function whose graph is symmetric with respect to the origin is said to be an odd function. For functions, the following two tests for symmetry are equivalent to tests (i) and (iii), respectively, on page 30. See FIGURES 2.2.2 and 2.2.3. The function whose graph is given in FIGURE 2.2.4 is neither even nor odd.

FIGURE 2.2.2 Even function; graph has y-axis symmetry

FIGURE 2.2.3 Odd function; graph has origin symmetry

Can you explain why the graph of a function cannot have symmetry with respect to the x-axis?

FIGURE 2.2.4 Function is neither even nor odd; no y-axis or origin symmetry

The graphical interpretation of these tests is illustrated in Figures 2.2.2 and 2.2.3. In Figure 2.2.2, observe that if f is an even function and

is also on its graph. Similarly we see in Figure 2.2.3 that if f is an odd function and

is on its graph.

EXAMPLE 1 Odd and Even Functions

(a) f(x) = x³ is an odd function since by (2),

Inspection of Figure 2.2.1(c) shows that the graph of f is symmetric with respect to the origin. For example, since f(1) = 1, (1, 1) is a point on the graph of y = x³. Because f is an odd function, f(−1) = −f(1) implies (−1, −1) is on the same graph.

(b) is an even function since by (1) and the laws of exponents

In Figure 2.2.1(i), we see that the graph of f is symmetric with respect to the y-axis. For example, since is a point on the graph of . Because f is an even function, f(−8) = f(8) implies (−8, 4) is on the same graph.

(c) f(x) = x³ + 1 is neither even nor odd. From

we see that f(–x) ≠ f(x), and f(–x) ≠ −f(x).

The graphs in Figure 2.2.1, with part (g) the only exception, possess either y-axis or origin symmetry. The functions in Figures 2.2.1(b), (d), (f), and (i) are even, whereas the functions in Figures 2.2.1(a), (c), (e), and (h) are odd.

Often we can sketch the graph of a function by applying a certain transformation to the graph of a simpler function (such as those given in Figure 2.2.1). We are going to consider two kinds of graphical transformations, rigid and nonrigid.

Rigid Transformations A rigid transformation of a graph is one that changes only the position of the graph in the xy-plane but not its shape. We have already examined this concept briefly in the discussion of the circle in Section 1.4. For example, the circle (x −2)² + (y − 3)² = 1 with center (2, 3) and radius r = 1 has exactly the same shape as the circle x² + y² = 1 with center at the origin. We can think of the graph of (x − 2)² + (y − 3)² = 1 as the graph of x² + y² = 1 shifted horizontally two units to the right followed by an upward vertical shift of three units. For the graph of a function y = f(x) we examine four kinds of shifts or translations.

Consider the graph of a function y = f(x) given in FIGURE 2.2.5. The shifts of this graph described in (i)–(iv) are the graphs in red in parts (a)–(d) of Figure 2.2.6. If (x, y) is a point on the graph of y = f(x) and the graph of f is shifted, say, upward by c > 0 units, then (x, y + c) is a point on the new graph. In general, the x-coordinates do not change as a result of a vertical shift. See FIGURES 2.2.6(a) and 2.2.6(b). Similarly, in a horizontal shift the y-coordinates of points on the shifted graph are the same as on the original graph. See Figures 2.2.6(c) and 2.2.6(d).

FIGURE 2.2.5 Graph of y = f(x)

FIGURE 2.2.6 Vertical and horizontal shifts of the graph of y = f(x) by an amount c > 0

EXAMPLE 2 Vertical and Horizontal Shifts

The graphs of y = x² + 1, y = x² − 1, y = (x + 1)²,and y = (x − 1)² are obtained from the graph of f(x) = x² in FIGURE 2.2.7(a) by shifting this graph, in turn, 1 unit up (Figure 2.2.7(b)), 1 unit down (Figure 2.2.7(c)), 1 unit to the left (Figure 2.2.7(d)), and 1 unit to the right (Figure 2.2.7(e)).

FIGURE 2.2.7 Shifted graphs in Example 2

Combining Shifts In general, the graph of a function

where c₁ and c₂ are positive constants, combines a horizontal shift (left or right) with a vertical shift (up or down). For example, the graph of y = f(x − c₁) + c₂ is the graph of y = f(x) shifted c₁ units to the right and then c₂ units up.

The order in which the shifts are done is irrelevant. We could do the upward shift first followed by the shift to the right.

EXAMPLE 3 Graph Shifted Vertically and Horizontally

Graph y = (x + 1)² − 1.

Solution From the preceding paragraph we identify in (3) the form y = f(x + c₁) − c₂ with c₁ = 1 and c₂ = 1. Thus, the graph of y = (x + 1)² − 1 is the graph of f(x) = x² shifted 1 unit to the left followed by a downward shift of 1 unit. The graph is given in FIGURE 2.2.8.

FIGURE 2.2.8 Shifted graph in Example 3

From the graph in Figure 2.2.8 we see immediately that the range of the function y = (x + 1)² − 1 = x² + 2x is the interval [−1, ∞) on the y-axis. Note also that the graph has x-intercepts (0, 0) and (−2, 0); you should verify this by solving x² + 2x = 0. Also, if you reexamine Figure 2.1.5 in Section 2.1 you will see that the graph of is the graph of the square root function (Figure 2.2.1(g)) shifted 3 units to the right and then 4 units up.

Another way of rigidly transforming a graph of a function is by a reflection in a coordinate axis.

In part (a) of FIGURE 2.2.9 we have reproduced the graph of a function y = f(x) given in Figure 2.2.5. The reflections of this graph described in (i)-(ii) are illustrated in Figures 2.2.9(b) and 2.2.9(c). If (x, y) denotes a point on the graph of y = f(x), then the point (x, −y) is on the graph of y = −f(x), and (−x, y) is on the graph of y = f(−x). Each of these reflections is a mirror image of the graph of y = f(x) in the respective coordinate axis.

FIGURE 2.2.9 Reflections in the coordinate axes

EXAMPLE 4 Reflections

Graph (a) (b)

Solution The starting point is the graph of given in FIGURE 2.2.10(a).

(a) The graph of is the reflection of the graph of in the x-axis. Observe in Figure 2.2.10(b) that since (1, 1) is on the graph of f, the point (1, − 1) is on the graph of .

(b) The graph of is the reflection of the graph of in the y-axis. Observe in Figure 2.2.10(c) that since (1, 1) is on the graph of f the point (− 1, 1) is on the graph of . The function looks a little strange, but bear in mind that its domain is determined by the requirement that −x ≥ 0, or equivalently x ≤ 0, and so the reflected graph is defined on the interval (−∞, 0].

Reflection or mirror image in a horizontal axis

Reflection or mirror image in a vertical axis

FIGURE 2.2.10 Graphs in Example 4

If a function f is even, then f (−x) = f (x) shows that a reflection in the y-axis would give precisely the same graph. If a function is odd, then from f (−x) = −f (x) we see that a reflection of the graph of f in the y-axis is identical to the graph of f reflected in the x-axis. In FIGURE 2.2.11 the blue curve is the graph of the odd function f(x) = x³; the red curve is the graph of y = f(−x) = (−x)³ = −x³. Notice that if the blue curve is reflected in either the y-axis or the x-axis, we get the red curve.

FIGURE 2.2.11 Reflection of an odd function in y-axis

Nonrigid Transformations If a function f is multiplied by a constant c > 0 the shape of the graph is changed but retains, roughly, its original shape. The graph of y = cf(x) is the graph of y = f(x) distorted vertically; the graph of f is either stretched (or elongated) vertically or is compressed (or flattened) vertically depending on the value of c. Stretching or compressing a graph are examples of nonrigid transformations.

If (x, y) represents a point on the graph of f, then the point (x, cy) is on the graph of cf. The graphs of y = x and y = 3x are compared in FIGURE 2.2.12; the y-coordinate of a point on the graph of y = 3x is 3 times as large as the y-coordinate of the point with the same x-coordinate on the graph of y = x. The comparison of the graphs of y = 10x² (blue graph) and (red graph) in FIGURE 2.1.13 is a little more dramatic; the graph of exhibits considerable vertical flattening, especially in a neighborhood of the origin. Note that c is positive in this discussion. To sketch the graph of y = −10x² we think of it as y = − (10x²), which means we first stretch the graph of y = x² vertically by a factor of 10 units and then reflect that graph in the x-axis.

FIGURE 2.2.12 Vertical stretch of the graph of f(x) = x

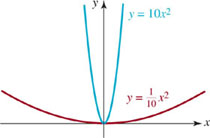
FIGURE 2.2.13 Vertical stretch (blue) and vertical compression (red) of the graph of f(x) = x²

The next example illustrates shifting, reflecting, and stretching of a graph.

EXAMPLE 5 Combining Transformations

Graph .

Solution You should recognize that the given function consists of four transformations of the basic function

We start with the graph of in FIGURE 2.2.14(a). Then stretch this graph vertically by a factor of 2 to obtain in Figure 2.2.14(b). Reflect this second graph in the x-axis to obtain in Figure 2.2.14(c). Shift this third graph 3 units to the right to obtain in Figure 2.2.14(d). Finally, shift the fourth graph upward 2 units to obtain in Figure 2.2.14(e). Note that the point (0, 0) on the graph of remains fixed in the vertical stretch and the reflection in the x-axis, but under the first (horizontal) shift (0, 0) moves to (3, 0) and under the second (vertical) shift (3, 0) moves to (3, 2).

FIGURE 2.2.14 Graph of function in Example 5

2.2 Exercises
Answers to selected odd-numbered problems begin on page ANS–3.

In Problems 1–10, use (1) and (2) to determine whether the given function y = f(x) is even, odd, or neither even nor odd. Do not graph.

1. f(x) = 4 − x²

2. f(x) = x² + 2x

3. f(x) = x³ − x + 4

4. f(x) = x⁵ + x³ + x

5.

6.

7.

8.

9. f(x) = |x³|

10. f(x) = x|x|

In Problems 11–14, classify the function y = f(x) whose graph is given as even, odd, or neither even nor odd.

11.

FIGURE 2.2.15 Graph for Problem 11

12.

FIGURE 2.2.16 Graph for Problem 12

13.

FIGURE 2.2.17 Graph for Problem 13

14.

FIGURE 2.2.18 Graph for Problem 14

In Problems 15–18, complete the graph of the given function y = f(x) if (a) f is an even function and (b) f is an odd function.

15.

FIGURE 2.2.19 Graph for Problem 15

16.

FIGURE 2.2.20 Graph for Problem 16

17.

FIGURE 2.2.21 Graph for Problem 17

18.

FIGURE 2.2.22 Graph for Problem 18

In Problems 19 and 20, suppose that f(−2) = 4 and f(3) = 7. Determine f(2) and f(−3).

19. If f is an even function.

20. If f is an odd function.

In Problems 21 and 22, suppose that g(−1) = −5 and g(4) = 8. Determine g(1) and g(−4).

21. If g is an odd function.

22. If g is an even function.

In Problems 23–32, the points (−2, 1) and (3, −4) are on the graph of the function y = f(x). Find the corresponding points on the graph obtained by the given transformations.

23. the graph of f shifted up 2 units

24. the graph of f shifted down 5 units

25. the graph of f shifted to the left 6 units

26. the graph of f shifted to the right 1 unit

27. the graph of f shifted up 1 unit and to the left 4 units

28. the graph of f shifted down 3 units and to the right 5 units

29. the graph of f reflected in the y-axis

30. the graph of f reflected in the x-axis

31. the graph of f stretched vertically by a factor of 15 units

32. the graph of f compressed vertically by a factor of unit, then reflected in the x-axis

In Problems 33–36, use the graph of the function y = f(x) given in the figure to graph the following functions.

(a) y = f(x) + 2

(b) y = f(x) − 2

(c) y = f(x + 2)

(d) y = f(x − 5)

(e) y = −f(x)

(f) y = f(−x)

33.

FIGURE 2.2.23 Graph for Problem 33

34.

FIGURE 2.2.24 Graph for Problem 34

35.

FIGURE 2.2.25 Graph for Problem 35

36.

FIGURE 2.2.26 Graph for Problem 36

In Problems 37 and 38, use the graph of the function y = f(x) given in the figure to graph the following functions.

(a) y = f(x) + 1

(b) y = f(x) − 1

(c) y = f(x + π)

(d) y = f(x − π/2)

(e) y =−f(x)

(f) y = f(−x)

(g) y = 3f(x)

(h)

37.

FIGURE 2.2.27 Graph for Problem 37

38.

FIGURE 2.2.28 Graph for Problem 38

In Problems 39–42, find the equation of the final graph after the given transformations are applied to the graph of y = f(x).

39. the graph of f(x) = x³ shifted up 5 units and right 1 unit

40. the graph of stretched vertically by a factor of 3 units, then shifted right 2 units

41. the graph of f(x) = x⁴ reflected in the x-axis, then shifted left 7 units

42. the graph of f(x) = 1/x reflected in the y-axis, then shifted left 5 units and down 10 units

In Problems 43–46, describe in words how the graph of the first function is obtained from the graph of the second function using rigid and nonrigid transformations. Carefully graph the first function.

43.

44.

45.

46.

For Discussion

47. Explain why the graph of a nonzero function cannot be symmetric with respect to the x-axis.

48. What points, if any, on the graph of y = f(x) remain fixed, that is, the same on the resulting graph after a vertical stretch or compression? After a reflection in the x-axis? After a reflection in the y-axis?

49. Discuss the relationship between the graphs of y = f(x) and y = f(|x|).

50. Discuss the relationship between the graphs of y = f(x) and y = f(cx), where c>0 is a constant. Consider two cases: 0 < c < 1 and c > 1.

51. Review the graphs of y = x and y = 1/x in Figure 2.2.1. Then discuss how to obtain the graph of the reciprocal y = 1/f(x) from the graph of y = f(x). Sketch the graph of y = 1/f(x) for the function f whose graph is given in Figure 2.2.26.

2.3 Linear Functions

Introduction The notion of a line plays an important role in the study of differential calculus. There are three types of lines in the xy- or Cartesian plane: horizontal lines, vertical lines, and slant or oblique lines. We will see in this section that an equation of each of these lines stems from a linear equation in two variables

where A, B, and C are real constants. The characteristic that gives (1) its name linear is that the variables x and y appear only to the first power. We will refer back to (1) when we review lines and their equations, but let’s note the cases of special interest:

The first and the third of these three equations define functions. By relabeling −C/B in (2) as b we get a constant function.

The domain of a constant function is the set of real numbers (−∞, ∞). In the definition of a function we are pairing each real number x with the same value of y, that is, (x, b). In our student/desk example of a function in Section 2.2 this is equivalent to having all the students in a classroom sit in one desk. On the other hand, the equation in (3) does not define a function. We cannot have one student (the fixed value of x) sit in all the desks in a classroom.

By relabeling −A/B and −C/B in (4) as a and b, respectively, we get the form of a linear function.

The domain of a linear function is the set of real numbers (−∞, ∞).

Graphs Since the graphs of constant and linear functions are straight lines, it is appropriate that we will review equations of all lines. We begin with the recollection from plane geometry that through any two distinct points (x₁, y₁) and (x₂, y₂) in the plane there passes only one line L. If x₁ ≠ x₂, then the number

is called the slope of the line determined by these two points. It is customary to call y₂ − y₁ the change in y or the rise of the line; x₂ − x₁ is the change in x or the run of the line. Therefore (7) is

See FIGURE 2.3.1(a). Any pair of distinct points on a line will determine the same slope. To see why this is so, consider the two similar right triangles in Figure 2.3.1(b). Since we know that the ratios of corresponding sides in similar triangles are equal we have

Hence the slope of a line is independent of the choice of points on the line.

FIGURE 2.3.1 Slope of a line

In FIGURE 2.3.2 we compare the graphs of lines with positive, negative, zero, and undefined slopes. In Figure 2.3.2(a) we see, reading the graph from left to right, that a line with positive slope (m > 0) rises as x increases. Figure 2.3.2(b) shows that a line with negative slope (m < 0) falls as x increases. If (x₁, y₁) and (x₂, y₂) are points on a horizontal line, then y₁ = y₂ and so its rise is y₂ − y₁ = 0. Hence from (7) the slope is zero (m = 0). See Figure 2.3.2(c). If (x₁, y₁) and (x₂, y₂) are points on a vertical line, then x₁ = x₂ and so its run is x₂ − x₁ = 0. In this case we say that the slope of the line is undefined or that the line has no slope. See Figure 2.3.2(d).

FIGURE 2.3.2 Lines with slope (a)–(c); line with no slope (d)

Point-Slope Equation We are now in a position to find an equation of a line L. To begin, suppose L has slope m and that (x₁, y₁) is on the line. If (x, y) represents any other point on L, then (7) gives

Multiplying both sides of the last equality by x − x_l gives an important equation.

EXAMPLE 1 Point-Slope Equation

Find an equation of the line with slope 6 and passing through .

Solution Letting m = 6, , y₁ = 2 we obtain from (8)

Simplifying gives

EXAMPLE 2 Point-Slope Equation

Find an equation of the line passing through the points (4, 3) and (−2, 5).

Solution First we compute the slope of the line through the points. From (7),

The point-slope equation (8) then gives

Slope-Intercept Equation Any line with slope (that is, any line that is not vertical) must cross the y-axis. If this y-intercept is (0, b), then with x₁ = 0, y₁ = b, the point-slope form (8) gives y − b = m(x − 0). The last equation simplifies to the next result.

The distributive law a(b + c) = ab + ac is the source of many errors on students’ papers. A common error goes something like this:

The correct result is:

Family of Lines For m ≠ 0, (8) and (9) give us the form of the linear function in (6). The coefficient a in (6) is, of course, the slope m of the line. When b = 0 in (9), the equation y = mx represents a family of lines that pass through the origin (0, 0). In FIGURE 2.3.3 we have drawn a few of the members of that family.

FIGURE 2.3.3 Lines through the origin are y = mx

EXAMPLE 3 Example 2 Revisited

We can also use the slope-intercept from (9) to obtain the equation of the line through two points in Example 2. As in that example, we start by finding the slope . The equation of the line is then . Substituting the coordinates of either point (4, 3) or (−2, 5) into the last equation enables us to determine b. If we use x = 4 and y = 3, then and so . The equation of the line is .

Horizontal and Vertical Lines We saw in Figure 2.3.2(c) that a horizontal line has slope m = 0. An equation of a horizontal line passing through a point (a, b) can be obtained from (8), that is, y − b = 0(x − a). The equation of a horizontal line is then

We have already seen this in (5) and in (2) where −C/B played the part of the symbol b. A vertical line through (a, b) has undefined slope and all points on the line have the same x-coordinate. The equation of a vertical line is then

Equation (11) is (3) with −C/A replaced by the symbol a.

EXAMPLE 4 Vertical and Horizontal Lines

Find equations for the vertical and horizontal lines through (3, −1). Graph these lines.

Solution Any point on the vertical line through (3, −1) has x-coordinate 3. The equation of this line is then x = 3. Similarly, any point on the horizontal line through (3, −1) has y-coordinate −1. The equation of this line is y = −1. Both lines are graphed in FIGURE 2.3.4. Don’t forget, only y = −1 is a function.

FIGURE 2.3.4 Horizontal and vertical lines in Example 4

Parallel and Perpendicular Lines Suppose L₁ and L₂ are two distinct lines with slope. This assumption means that both L₁ and L₂ are nonvertical lines. Then necessarily L₁ and L₂ are either parallel or they intersect. If the lines intersect at a right angle they are said to be perpendicular. We can determine whether two lines are parallel or are perpendicular by examining their slopes.

There are several ways of proving these theorems. The proof of (12) can be obtained using similar right triangles, as in FIGURE 2.3.5, and the fact that the ratios of corresponding sides in such triangles are equal. We leave the justification of (13) as an exercise. See Problem 64 in Exercises 2.3. Note that the condition m₁m₂ = − 1 implies that m₂ = −1/m₁, that is, the slopes are negative reciprocals of each other. A horizontal line y = b and a vertical line x = a are perpendicular, but the latter is a line with no slope.

Parallel lines

FIGURE 2.3.5 Parallel lines

EXAMPLE 5 Parallel Lines

The linear equations 3x + y = 2 and 6x + 2y = 15 can be rewritten in the slope-intercept forms

respectively. As noted in color in the preceding line the slope of each line is −3. Therefore the lines are parallel. The graphs of these equations are shown in FIGURE 2.3.6.

FIGURE 2.3.6 Parallel lines in Example 5

EXAMPLE 6 Perpendicular Lines

Find an equation of the line through (0, −3) that is perpendicular to the graph of 4x − 3y + 6 = 0.

Solution We express the given linear equation in slope-intercept form:

Dividing by 3 gives . This line, whose graph is given in blue in FIGURE 2.3.7, has slope . The slope of any line perpendicular to it is the negative reciprocal of , namely, . Since (0, −3) is the y-intercept of the required line, it follows from (9) that its equation is . The graph of the last equation is the red line in Figure 2.3.7.

FIGURE 2.3.7 Perpendicular lines in Example 6

Graphs As mentioned in the earlier sections of this chapter, when graphing an equation it is always a good habit to try to find x- and y-intercepts of its graph. Except in the cases of horizontal and vertical lines, and lines through the origin, a line will have distinct x- and y-intercepts. Of course, that is all we need to draw a line: two points.

EXAMPLE 7 Graph of a Linear Equation

Graph the linear equation 3x − 2y + 8 = 0.

Solution There is no need to rewrite the linear equation in the form y = mx + b. We simply find the intercepts.

y-intercept:	Setting x = 0 gives − 2y + 8 = 0 or y = 4. The y-intercept is (0, 4).
x-intercept:	Setting y = 0 gives 3x + 8 = 0 or . The x-intercept is .

As shown in FIGURE 2.3.8, the line is drawn through the two intercepts (0, 4) and

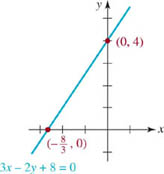
FIGURE 2.3.8 Graph of equation in Example 7

Increasing-Decreasing Functions We have just seen in Figures 2.3.2(a) and 2.3.2(b) that if a > 0 (which, as we have just seen plays the part of m) the values of a linear function f(x) = ax + b increase as x increases, whereas for a < 0, the values f(x) decrease as x increases. The notions of increasing and decreasing can be extended to any function. The ability to determine intervals over which a function f is either increasing or decreasing plays an important role in applications of calculus.

In FIGURE 2.3.9(a) the function f is increasing on the interval [a, b], whereas f is decreasing on [a, b] in Figure 2.3.9(b). A linear function f(x) = ax + b increases on the interval (−∞, ∞) for a > 0 and decreases on the interval (−∞, ∞) for a < 0.

FIGURE 2.3.9 Increasing function in (a); decreasing function in (b)

Points of Intersection We are often interested in finding the points where the graphs of two functions intersect. The x-intercepts of the graph of a function f can be interpreted as the points where the graph of f intersects the graph of the constant function y = 0. In general, at a point P of intersection of the graphs of two functions f and g, the coordinates (x, y) of P must satisfy both equations y = f(x)and y = g(x),and so f(x) = g(x).

EXAMPLE 8 Intersecting Lines

Find the point where the two lines in Figure 2.3.7 intersect.

Solution We equate and solve for x:

By substituting into either equation we find that . The point of intersection of the lines is .

2.3 Exercises
Answers to selected odd-numbered problems begin on page ANS–4.

In Problems 1–6, find the slope of the line through the given points. Graph the line through the points.

1. (3, −7), (1, 0)

2. (−4, −1), (1, −1)

3. (5, 2), (4, −3)

4. (1, 4), (6, −2)

5. (−1, 2), (3, −2)

6.

In Problems 7 and 8, use the graph of the given line to estimate its slope.

7.

FIGURE 2.3.10 Graph for Problem 7

8.

FIGURE 2.3.11 Graph for Problem 8

In Problems 9–16, find the slope and the x- and y-intercepts of the given line. Graph the line.

9. 3x − 4y + 12 = 0

10.

11. 2x − 3y = 9

12. −4x − 2y + 6 = 0

13. 2x + 5y − 8 = 0

14.

15.

16. y = 2x + 6

In Problems 17–22, find an equation of the line through (1, 2) with the indicated slope.

17.

18.

19. 0

20. −2

21. −1

22. undefined

In Problems 23–36, find an equation of the line that satisfies the given conditions.

23. through (2, 3) and (6, −5)

24. through (5, −6) and (4, 0)

25. through (8, 1) and (−3, 1)

26. through (2, 2) and (−2, −2)

27. through (−2, 0) and (−2, 6)

28. through (0, 0) and (a, b)

29. through (−2, 4) parallel to 3x + y − 5 = 0

30. through (1, −3) parallel to 2x − 5y + 4 = 0

31. through (5, −7) parallel to the y-axis

32. through the origin parallel to the line through (1, 0) and (−2, 6)

33. through (2, 3) perpendicular to x − 4y + 1 = 0

34. through (0, −2) perpendicular to 3x + 4y + 5 = 0

35. through (−5, −4) perpendicular to the line through (1, 1) and (3, 11)

36. through the origin perpendicular to every line with slope 2

37. Find the coordinates of the point P shown in FIGURE 2.3.12.

FIGURE 2.3.12 Lines in Problem 37

38. A line through (2, 4) has slope 8. Without finding an equation of the line, determine whether the point (1, −5) is on the line.

In Problems 39–42, determine which of the given lines are parallel to each other and which are perpendicular to each other.

39. (a) 3x − 5y + 9 = 0

(b) 5x = −3y

(c) −3x + 5y = 2

(d) 3x + 5y + 4 = 0

(e) −5x − 3y + 8 = 0

(f) 5x − 3y − 2 = 0

40. (a) 2x + 4y + 3 = 0

(b) 2x − y = 2

(c) x + 9 = 0

(d) x = 4

(e) y − 6 = 0

(f) −x − 2y + 6 = 0

41. (a) 3x − y − 1 = 0

(b) x − 3y + 9 = 0

(c) 3x + y = 0

(d) x + 3y = 1

(e) 6x − 3y + 10 = 0

(f) x + 2y = −8

42. (a) y + 5 = 0

(b) x = 7

(c) 4x + 6y = 3

(d) 12x − 9y + 7 = 0

(e) 2x − 3y − 2 = 0

(f) 3x + 4y − 11 = 0

In Problems 43 and 44, find a linear function (6) that satisfies both of the given conditions.

43. f (−1) = 5, f(1) = 6

44. f (−1) = 1 + f(2), f(3) = 4f(1)

In Problems 45–48, find the point of intersection of the graphs of the given linear functions. Sketch both lines.

45. f(x) = −2x + 1, g(x) = 4x + 6

46.

47.

48. f(x) = 2x − 10, g(x) = −3x

In Problems 49 and 50, for the given linear function compute the quotient

where h is a constant.

49. f(x) = −9x + 12

50.

51. Find an equation of the red line L shown in FIGURE 2.3.13 if an equation of the blue curve is y = x² + 1.

FIGURE 2.3.13 Graphs for Problem 51

52. A tangent line L to a circle at a point P on the circle is perpendicular to the line through P and the center of the circle. Find an equation of the red line L shown in FIGURE 2.3.14.

FIGURE 2.3.14 Circle and tangent line in Problem 52

Miscellaneous Applications

53. Thermometers The functional relationship between degrees Celsius T_C and degrees Fahrenheit T_F is linear.

(a) Express T_F as a function of T_C if (0°C, 32°F) and (60°C, 140°F) are on the graph of T_F.

(b) Show that 100°C is equivalent to the Fahrenheit boiling point 212°F. See FIGURE 2.3.15.

FIGURE 2.3.15 Thermometers in Problems 53 and 54

54. Thermometers––Continued The functional relationship between degrees Celsius T_C and temperature measured in kelvin units T_K is linear.

(a) Express T_K as a function of T_C if (0°C, 273K) and (27°C, 300K) are on the graph of T_K.

(b) Express the boiling point of water 100°C in kelvin units. See Figure 2.3.15.

(c) Absolute zero is defined as 0 K. What is 0 K in degrees Celsius?

(d) Express T_K as a linear function of T_F.

(e) What is 0 K in degrees Fahrenheit?

55. Simple Interest In simple interest, the amount A accrued over time is the linear function A = P + Prt, where P is the principal, t is measured in years, and r is the annual interest rate (expressed as a decimal). Compute A after 20 years if the principal is P = 1000 and the annual interest rate is 3.4%. At what time is A = 2200?

56. Linear Depreciation Straight line, or linear, depreciation consists of an item losing all its initial worth of A dollars over a period of n years by an amount A/n each year. If an item costing $20,000 when new is depreciated linearly over 25 years, determine a linear function giving its value V after x years, where 0 < x < 25. What is the value of the item after 10 years?

For Discussion

57. Consider the linear function . If x is changed by 1 unit, how many units will y change? If x is changed by 2 units? If x is changed by n (n a positive integer) units?

58. Consider the interval [x₁, x₂] and the linear function f(x) = ax + b, a ≠ 0. Show that

and interpret this result geometrically for a > 0.

59. How would you find an equation of the line that is the perpendicular bisector of the line segment through ?

60. Using only the concepts of this section, how would you prove or disprove that the triangle with vertices (2, 3), (−1, −3), and (4, 2) is a right triangle?

61. Using only the concepts of this section, how would you prove or disprove that the quadrilateral with vertices (0, 4), (−1, 3), (−2, 8), and (−3, 7) is a parallelogram?

62. If C is an arbitrary real constant, the equation 2x − 3y = C defines a family of lines. Choose four different values of C and plot the corresponding lines on the same coordinate axes. What is true about the lines that are members of this family?

63. Find the equations of the lines through (0, 4) that are tangent to the circle x² + y² = 4.

64. To prove (13) you have to prove two things, the “only if” and the “if” parts of the theorem.

(a) In FIGURE 2.3.16, without loss of generality, we have assumed that two perpendicular lines, y = m₁x, m₁ > 0 and y = m₂x, m₂ < 0, intersect at the origin. Use the information in the figure to prove the “only if” part:

FIGURE 2.3.16 Lines through origin in Problem 64

If L₁ and L₂ are perpendicular lines with slopes m₁ and m₂, then m₁m₂ = −1.

(b) Reverse your argument in part (a) to prove the “if” part:

If L₁ and L₂ are lines with slopes m₁ and m₂ such that m₁m₂ = −1, then L₁ and L₂ are perpendicular.

2.4 Quadratic Functions

Introduction The squaring function y = x² that played an important role in Section 2.2 is a member of a family of functions called quadratic functions.

The domain of a quadratic function f is the set of real numbers (−∞, ∞).

Graphs The graph of any quadratic function is called a parabola. The graph of a quadratic function has the same basic shape of the squaring function y = x² shown in FIGURE 2.4.1. In the examples that follow we will see that the graphs of quadratic functions (1) are simply transformations of the graph of y = x²:

FIGURE 2.4.1 Graph of simplest parabola

• The graph of f(x) = ax², a > 0, is the graph of y = x² stretched vertically when a > 1, and compressed vertically when 0 < a < 1.
• The graph of f(x) = ax², a < 0, is the graph of y = ax², a > 0, reflected in the x-axis.
• The graph of f(x) = ax² + bx + c, b ≠ 0, is the graph of y = ax² shifted horizontally or vertically.

From the first two items in the bulleted list, we conclude that the graph of a quadratic function opens upward (as in Figure 2.4.1) if a > 0 and opens downward if a < 0.

EXAMPLE 1 Stretch, Compression, and Reflection

(a) The graphs of y = 4x² and are, respectively, a vertical stretch and a vertical compression of the graph of y = x². The graphs of these functions are shown in FIGURE 2.4.2(a); the graph of y = 4x² is shown in red, the graph of is green, and the graph of y = x² is blue.

(b) The graphs of y = −4x², , y = −x² are obtained from the graphs of the functions in part (a) by reflecting their graphs in the x-axis. See Figure 2.4.2(b).

FIGURE 2.4.2 Graphs of quadratic functions in Example 1

Vertex and Axis If the graph of a quadratic function opens upward a > 0 (or downward a < 0), the lowest (highest) point (h, k) on the parabola is called its vertex. All parabolas are symmetric with respect to a vertical line through the vertex (h, k). The line x = h is called the axis of symmetry or simply the axis of the parabola. See FIGURE 2.4.3.

FIGURE 2.4.3 Vertex and axis of a parabola

Standard Form The vertex of a parabola can be determined by recasting the equation f(x) = ax² + bx + c into the standard form

The form (2) is obtained from the equation (1) by completing the square in x. Completing the square in (1) starts with factoring the number a from all terms involving the variable x:

Within the parentheses we add and subtract the square of one-half the coefficient of x:

The last expression is equation (2) with the identifications h = −b/2a and k = (4ac − b²)/4a. If a > 0, then necessarily a (x − h)² ≥ 0. Hence f(x) in (2) is a minimum when (x − h)² = 0, that is, for x = h. A similar argument shows that if a < 0 in (2), f(x) is a maximum value for x = h. Thus (h, k) is the vertex of the parabola. The equation of the axis of the parabola is x = h or x = −b/2a.

If a > 0, then the function f in (2) is decreasing on the interval (−∞, h] and increasing on the interval [h, ∞). If a < 0, we have just the opposite, that is, f is increasing on (−∞, h] followed by decreasing on [h, ∞).

We strongly suggest that you do not memorize the result in the last line of (3), but practice completing the square each time. However, if memorization is permitted by your instructor to save time, then the vertex can be found by computing the coordinates of the point

Intercepts The graph of (1) always has a y-intercept since f(0) = c, and so the y-intercept is (0, c). To determine whether the graph has x-intercepts we must solve the equation f(x) = 0. The last equation can be solved either by factoring or by using the quadratic formula. Recall that a quadratic equation ax² + bx + c = 0, a ≠ 0, has the solutions

We distinguish three cases according to the algebraic sign of the discriminant b² − 4ac.

•    If b² − 4ac > 0, then there are two distinct real solutions x₁ and x₂. The parabola crosses the x-axis at (x₁, 0) and (x₂, 0).

•    If b² − 4ac = 0, then there is a single real solution x₁. The vertex of the parabola is located on the x-axis at (x₁, 0). The parabola is tangent to, or touches, the x-axis at this point.

•    If b² − 4ac < 0, then there are no real solutions. The parabola does not cross the x-axis.

See Section 1.4.

As the next example shows, a reasonable sketch of a parabola can be obtained by plotting the intercepts and the vertex.

EXAMPLE 2 Graph Using Intercepts and Vertex

Graph f(x) = x² − 2x − 3.

Solution Since a = 1 > 0 we know that the parabola will open upward. From f(0) = −3 we get the y-intercept (0, −3). To see whether there are any x-intercepts we solve x² − 2x − 3 = 0. By factoring

we find the solutions x = −1 and x = 3. The x-intercepts are (− 1, 0) and (3, 0). To locate the vertex we complete the square:

Thus the standard form is f(x) = (x − 1)² − 4. With the identifications h = 1 and k = −4, we conclude that the vertex is (1, −4). Using this information we draw a parabola through these four points as shown in FIGURE 2.4.4.

FIGURE 2.4.4 Parabola in Example 2

One last observation. By finding the vertex we automatically determine the range of a quadratic function. In our current example, y = −4 is the smallest number in the range of f and so the range of f is the interval [− 4, ∞) on the y-axis.

EXAMPLE 3 Vertex Is the x-intercept

Graph f(x) = −4x² + 12x − 9.

Solution The graph of this quadratic function is a parabola that opens downward because a = − 4 < 0. To complete the square we start by factoring −4 from the two x-terms:

Thus the standard form is . With and k = 0 we see that the vertex is . The y-intercept is (0, f(0)) = (0, −9). Solving −4x² + 12x − 9 = 0, we find that there is only one x-intercept, namely, . Of course, this was to be expected because the vertex is on the x-axis. As shown in FIGURE 2.4.5 a rough sketch can be obtained from these two points alone. The parabola is tangent to the x-axis at .

FIGURE 2.4.5 Parabola in Example 3

EXAMPLE 4 Using (4) to Find the Vertex

Graph f(x) = x² + 2x + 4.

Solution The graph is a parabola that opens upward because a = 1 > 0. For the sake of illustration we will use (4) this time to find the vertex. With b = 2, −b/2a = −2/2 = −1 and

the vertex is (−1, f(−1)) = (−1, 3). Now the y-intercept is (0, f(0)) = (0, 4) but the quadratic formula shows that the equation f(x) = 0 or x² + 2x + 4 = 0 has no real solutions. Therefore the graph has no x-intercepts. Since the vertex is above the x-axis and the parabola opens upward, the graph must lie entirely above the x-axis. See FIGURE 2.4.6.

FIGURE 2.4.6 Parabola in Example 4

Graphs by Transformations The standard form (2) clearly describes how the graph of any quadratic function is constructed from the graph of y = x² starting with a non-rigid transformation followed by two rigid transformations:

•    y = ax² is the graph of y = x² stretched or compressed vertically.

•    y = a(x − h)² is the graph of y = ax² shifted |h| units horizontally.

•    y = a(x − h)² + k is the graph of y = a(x − h)² shifted |k| units vertically.

FIGURE 2.4.7 illustrates the horizontal and vertical shifting in the case where a > 0,h > 0, and k > 0.

FIGURE 2.4.7 The red graph is obtained by shifting the blue graph h units to the right and k units upward.

EXAMPLE 5 Horizontally Shifted Graphs

Compare the graphs of (a) y = (x − 2)²and (b) y = (x + 3)².

Solution The blue dashed graph in FIGURE 2.4.8 is the graph of y = x². Matching the given functions with (2) shows in each case that a = 1 and k = 0. This means that neither graph undergoes a vertical stretch or compression, and neither graph is shifted vertically.

FIGURE 2.4.8 Shifted graphs in Example 5

(a) With the identification h = 2, the graph of y = (x − 2)² is the graph of y = x² shifted horizontally 2 units to the right. The vertex (0, 0) for y = x² becomes the vertex (2, 0) for y = (x − 2)². See the red graph in Figure 2.4.8.

(b) With the identification h = −3, the graph of y = (x + 3)² is the graph of y = x² shifted horizontally |−3| =3 units to the left. The vertex (0, 0) for y = x² becomes the vertex (−3, 0) for y = (x + 3)². See the green graph in Figure 2.4.8.

EXAMPLE 6 Shifted Graph

Graph y = 2(x − 1)² − 6.

Solution The graph is the graph of y = x² stretched vertically upward, followed by a horizontal shift to the right of 1 unit, followed by a vertical shift downward of 6 units. In FIGURE 2.4.9, you should note how the vertex (0, 0) on the graph of y = x² is moved to 11, 26) on the graph of y = 2(x − 1)² − 6 as a result of these transformations. You should also follow how the point (1, 1) shown in Figure 2.4.9(a) ends up as (2, −4) in Figure 2.4.9(d).

FIGURE 2.4.9 Graphs in Example 6

Graphs can be of help in solving certain inequalities when a sign chart is not useful because the quadratic does not factor conveniently. For example, the quadratic function in Example 6 is equivalent to y = 2x² − 4x − 4. Were we required to solve the inequality 2x² − 4x − 4 ≥ 0, we see in Figure 2.4.9(d) that y > 0 to the left of the x-intercept on the negative x-axis and to the right of the x-intercept on the positive x-axis. The x-coordinates of these intercepts, obtained by solving 2x² − 4x − 4 = 0 by the quadratic formula, are . Thus the solution of 2x² − 4x − 4 ≥ 0 is .

Freely Falling Object Suppose an object, such as a ball, is either thrown straight upward (downward) or simply dropped from an initial height s₀. Then if the positive direction is taken to be upward, the height s(t) of the object above ground is given by the quadratic function

where g is the acceleration due to gravity (−32 ft/s² or −9.8 m/s²), v₀ is the initial velocity imparted to the object, and t is time measured in seconds. See FIGURE 2.4.10. If the object is dropped, then v₀ = 0. An assumption in the derivation of (5), a straightforward exercise in integral calculus, is that the motion takes place close to the surface of Earth and so the retarding effects of air resistance is ignored. Also, the velocity of the object while it is in the air is given by the linear function

FIGURE 2.4.10 Rock thrown upward from an initial height s₀

See Problems 49–52 in Exercises 2.4.

2.4 Exercises
Answers to selected odd-numbered problems begin on page ANS–5.

In Problems 1–6, sketch the graph of the given function f.

1. f(x) = 2x²

2. f(x) = −2x²

3. f(x) = 2x² − 2

4. f(x) = 2x² + 5

5. f(x) = −2x² + 1

6. f(x) = −2x² − 3

In Problems 7–18, consider the quadratic function f.

(a) Find all intercepts of the graph of f.

(b) Express the function f in standard form.

(c) Find the vertex and axis of symmetry.

(d) Sketch the graph of f.

7. f(x) = x(x + 5)

8. f(x) = −x² + 4x

9. f(x) = (3 − x) (x + 1)

10. f(x) = (x − 2)(x − 6)

11. f(x) = x² − 3x + 2

12. f(x) = − x² + 6x − 5

13. f(x) = 4x² − 4x + 3

14. f(x) = −x² + 6x − 10

15.

16. f(x) = x² − 2x − 7

17. f(x) = x² − 10x + 25

18. f(x) = −x² + 6x − 9

In Problems 19 and 20, find the maximum or the minimum value of the function f. Give the range of the function f.

19. f(x) = 3x² − 8x + 1

20. f(x) = −2x² − 6x + 3

In Problems 21–24, find the largest interval on which the function f is increasing and the largest interval on which f is decreasing.

21.

22. f(x) = − (x + 10)²

23. f(x) = −2x² − 12x

24. f(x) = x² + 8x − 1

In Problems 25–30, describe in words how the graph of the given function can be obtained from the graph of y = x² by rigid or nonrigid transformations.

25. f(x) = (x − 10)²

26. f(x) = (x + 6)²

27.

28. f(x) = 10(x − 2)² − 1

29. f(x) = (−x − 6)² − 4

30. f(x) = − (1 − x)² + 1

In Problems 31–36, the given graph is the graph of y = x² shifted/reflected in the xy-plane. Write an equation of the graph.

31.

FIGURE 2.4.11 Graph for Problem 31

32.

FIGURE 2.4.12 Graph for Problem 32

33.

FIGURE 2.4.13 Graph for Problem 33

34.

FIGURE 2.4.14 Graph for Problem 34

35.

FIGURE 2.4.15 Graph for Problem 35

36.

FIGURE 2.4.16 Graph for Problem 36

In Problems 37 and 38, find a quadratic function f(x) = ax² + bx + c that satisfies the given conditions.

37. f has the values f(0) = 5, f(1) = 10, f(−1) =4

38. graph passes through (2, −1), zeros of f are 1 and 3

In Problems 39 and 40, find a quadratic function in standard form f(x) = a(x − h)² + k that satisfies the given conditions.

39. the vertex of the graph of f is (1, 2), graph passes through (2, 6)

40. the maximum value of f is 10, axis of symmetry is x = −1, and y-intercept is (0, 8)

In Problems 41–44, sketch the region in the xy-plane that is bounded between the graphs of the given functions. Find the points of intersection of the graphs.

41. y = −x + 4, y = x² + 2x

42. y = 2x − 2, y = 1 − x²

43. y = x² + 2x + 2, y = −x² − 2x + 2

44. y = x² − 6x + 1, y = 2x² + 2x + 1

45. Find the maximum value of . [Hint: See Problems 19 and 20. Let

46. Consider the graphs shown in FIGURE 2.4.17. Find the points on both graphs for 1 ≤ x ≤ 6 such that the vertical distance d between the graphs is a maximum. What is the maximum vertical distance?

FIGURE 2.4.17 Graphs for Problem 46

47. (a) Express the square of the distance d from the point (x, y) on the graph of y = 2x to the point (5, 0) shown in FIGURE 2.4.18 as a function of x.

FIGURE 2.4.18 Distance in Problem 47

(b) Use the function in part (a) to find the point (x, y) that is closest to (5, 0).

48. As shown in FIGURE 2.4.19, an arrow that is shot at a 45° angle with the horizontal travels along a parabolic arc defined by the equation y = ax² + x + c. Use the fact that the arrow is launched at a vertical height of 6 ft and travels a horizontal distance of 200 ft to find the coefficients a and c. What is the maximum height attained by the arrow?

FIGURE 2.4.19 Arrow in Problem 48

49. An arrow is shot vertically upward with an initial velocity of 64 ft/s from a point 6 ft above the ground. See FIGURE 2.4.20.

FIGURE 2.4.20 Arrow in Problem 49

(a) Find the height s(t) and the velocity v(t) of the arrow at time t ≥ 0.

(b) What is the maximum height attained by the arrow? What is the velocity of the arrow at the time the arrow attains its maximum height?

(c) At what time does the arrow fall back to the 6-ft level? What is its velocity at this time?

50. The height above ground of a toy rocket launched upward from the top of a building is given by s(t) = −16t² + 96t + 256.

(a) What is the height of the building?

(b) What is the maximum height attained by the rocket?

(c) Find the time when the rocket strikes the ground.

51. A ball is dropped from the roof of a building that is 122.5 meters above ground level.

(a) What is the height and velocity of the ball at t = 1 s?

(b) At what time does the ball hit the ground?

(c) What is the impact velocity of the ball when it hits the ground?

52. A few years ago a newspaper in the Midwest reported that an escape artist was planning to jump off a bridge into the Mississippi River wearing 70 lb of chains and manacles. The newspaper article stated that the height of the bridge was 48 ft and predicted that the escape artist’s impact velocity on hitting the water would be 85 mi/h. Assuming that he simply dropped from the bridge, then his height (in feet) and velocity (in feet/second) t seconds after jumping off the bridge are given by the functions s(t) = −16t² + 48 and v(t) = −32t, respectively. Determine whether the newspaper’s estimate of his impact velocity was accurate.

Miscellaneous Applications

53. Spread of a Disease One model for the spread a flu virus assumes that within a population of P persons the rate at which a disease spreads is jointly proportional to the number D of persons already carrying the disease and the number P − D of persons not yet infected. Mathematically, the model is given by the quadratic function

where R(D) is the rate of spread of the flu virus (in cases per day) and k > 0 is a constant of proportionality.

(a) Show that if the population P is a constant, then the disease spreads most rapidly when exactly one-half the population is carrying the flu.

(b) Suppose that in a town of 10,000 persons, 125 are sick on Sunday, and 37 new cases occur on Monday. Estimate the constant k.

(c) Use the result of part (b) to estimate the number of new cases on Tuesday. [Hint: The number of persons carrying the flu on Monday is 162 = 125 + 37.]

(d) Estimate the number of new cases on Wednesday, Thursday, Friday, and Saturday.

Spreading a virus

For Discussion

54. In Problems 50 and 52, what is the domain of the function s(t)? [Hint: It is not (−∞, ∞).]

55. On the Moon the acceleration due to gravity is one-sixth the acceleration due to gravity on Earth. If a ball is tossed vertically upward from the surface of the Moon, would it attain a maximum height six times that on Earth when the same initial velocity is used? Defend your answer.

56. Suppose the quadratic function f(x) = ax² + bx + c has two distinct real zeros. How would you prove that the x-coordinate of the vertex is the midpoint of the line segment between the x-coordinates of the intercepts? Carry out your ideas.

2.5 Piecewise-Defined Functions

Introduction A function f may involve two or more expressions or formulas, with each formula defined on different parts of the domain of f. A function defined in this manner is called a piecewise-defined function. For example,

is not two functions, but a single function in which the rule of correspondence is given in two pieces. In this case, one piece is used for the negative real numbers (x < 0) and the other part on the nonnegative numbers (x ≥ 0); the domain of f is the union of the intervals (−∞, 0) ∪ [0, ∞) = (− ∞, ∞). For example, since −4 < 0, the rule indicates that we square the number:

on the other hand, since 6 ≥ 0 we add 1 to the number:

The USPS first-class mailing rates for a letter, a card, or a package provide a real-world illustration of a piecewise-defined function. As of this writing, the postage for sending a letter in a standard-size envelope by first-class mail depends on its weight in ounces:

The rule in (1) is a function P consisting of 13 pieces (letters over 13 ounces are sent priority mail). A value P(w) is one of thirteen constants; the constant changes depending on the weight w (in ounces) of the letter. For example,

The domain of the function P is the union of the intervals:

EXAMPLE 1 Graph of a Piecewise-Defined Function

Graph the piecewise-defined function

Solution Although the domain of f consists of all real numbers (−∞, ∞), each piece of the function is defined on a different part of this domain. We draw

• the horizontal line y = − 1 for x < 0,
• the point (0, 0) for x = 0, and
• the line y = x + 1 for x > 0.

The graph is given in FIGURE 2.5.1.

FIGURE 2.5.1 Graph of piecewise-defined function in Example 1

The solid dot at the origin in Figure 2.5.1 indicates that the function in (2) is defined at x = 0 only by f(0) = 0; the open dots indicate that the formulas corresponding to x < 0 and to x > 0 do not define f at x = 0. Since we are making up a function, consider the definition:

The graph of g shown in FIGURE 2.5.2 is very similar to the graph of (2), but (2) and (3) are not the same function since f(0) = 0 but g(0) = − 1.

FIGURE 2.5.2 Graph of function g defined in (3)

Greatest Integer Function We consider next a piecewise-defined function that is similar to the “postage stamp” function (1) in that both are examples of step functions; each function is constant on an interval and then jumps to another constant value on the next abutting interval. This new function, which has many notations, will be denoted here by f(x) = [x], and is defined by the rule

The function f is called the greatest integer function because (4), translated into words, means that:

F(x) is the greatest integer n that is less than or equal to x.

For example,

and so on. The domain of f is the set of real numbers and consists of the union of an infinite number of disjoint intervals; in other words, f(x) = [x] is a piecewise-defined function given by

The range of f is the set of integers. A portion of the graph of f is given on the closed interval [−2, 5 ] in FIGURE 2.5.3.

FIGURE 2.5.3 Greatest integer function

In computer science the greatest integer function is known as the floor function and is denoted by f(x) = [x]. See Problems 47, 48, and 53 in Exercises 2.5.

EXAMPLE 2 Shifted Graph

Graph y = [x −2].

Solution The function is y = f(x − 2), where f(x) = [x]. Thus the graph in Figure 2.5.3 is shifted horizontally 2 units to the right. Note in Figure 2.5.3 that if n is an integer, then f(n) = [n] = n. But in FIGURE 2.5.4, for x = n, y = n − 2

FIGURE 2.5.4 Shifted graph in Example 2

Continuous Functions The graph of a continuous function has no holes, finite gaps, or infinite breaks. While the formal definition of continuity of a function is an important topic of discussion in calculus, in this course it suffices to think in informal terms. A continuous function is often characterized by saying that its graph can be drawn “without lifting pencil from paper.” Parts (a)−(c) of Figure 2.5.5 illustrate functions that are not continuous, or discontinuous, at x = 2. The function

in FIGURE 2.5.5(a) has a hole in its graph (there is no point (2, f (2))); the function in Figure 2.5.5(b) has a finite gap or jump in its graph at x = 2; the function in Figure 2.5.5(c) has an infinite break in its graph at x = 2. The function f(x) = x³ − 3x + 2 is continuous; its graph given in Figure 2.5.5(d) has no holes, gaps, or infinite breaks.

FIGURE 2.5.5 Discontinuous functions (a)–(c); continuous function (d)

You should be aware that constant functions, linear functions, and quadratic functions are continuous. Piecewise-defined functions can be continuous or discontinuous. The functions given in (2), (3), and (4) are discontinuous.

Absolute-Value Function The function y = |x|, called the absolute-value function, appears frequently in the study of calculus. To obtain the graph, we graph its two pieces consisting of perpendicular half lines:

See FIGURE 2.5.6(a). Since y ≥ 0 for all x, another way of graphing (6) is simply to sketch the line y = x and then reflect in the x-axis that portion of the line that is below the x-axis. See Figure 2.5.6(b). The domain of (6) is the set of real numbers (−∞, ∞), and as is seen in Figure 2.5.6(a), the absolute-value function is an even function, decreasing on the interval (− ∞, 0), increasing on the interval (0, ∞), and is continuous.

FIGURE 2.5.6 Absolute-value function (6)

In some applications we are interested in the graph of the absolute value of an arbitrary function y = f(x); in other words, y = | f(x) |. Since | f(x) | is nonnegative for all numbers x in the domain of f, the graph of y = | f(x)| does not extend below the x-axis. Moreover, the definition of the absolute value of f(x),

shows that we must negate f(x) whenever f(x) is negative. There is no need to worry about solving the inequalities in (7); to obtain the graph of y = |f (x)|, we can proceed just as we did in Figure 2.5.6(b): Carefully draw the graph of y = f(x) and then reflect in the x-axis all portions of the graph that are below the x-axis.

EXAMPLE 3 Absolute Value of a Function

Graph y = | −3x + 2|.

Solution We first draw the graph of the linear function f(x) = −3x + 2. Note that since the slope is negative, f is decreasing and its graph crosses the x-axis at . We dash the graph for since that portion is below the x-axis. Finally, we reflect that portion upward in the x-axis to obtain the solid blue v-shaped graph in FIGURE 2.5.7. Since f(x) = x is a simple linear function, it is not surprising that the graph of the absolute value of any linear function f(x) = ax + b, a ≠ 0, will result in a graph similar to that of the absolute-value function shown in Figure 2.5.6(a).

FIGURE 2.5.7 Graph of function in Example 3

EXAMPLE 4 Absolute Value of a Function

Graph y = |−x² + 2x + 3|.

Solution As in Example 3, we begin by drawing the graph of the function f(x) = −x² + 2x + 3 by finding its intercepts (−1, 0), (3, 0), (0, 3) and, since f is a quadratic function, its vertex (1, 4). Observe in FIGURE 2.5.8(a) that y < 0 for x < −1 and for x > 3. These portions of the graph of f are reflected in the x-axis to obtain the graph of y = |−x² + 2x + 3| given in Figure 2.5.8(b).

FIGURE 2.5.8 Graphs of functions in Example 4

2.5 Exercises
Answers to selected odd-numbered problems begin on page ANS–6.

In Problems 1–4, find the indicated values of the given piecewise-defined function f.

1.

2.

3.

4.

5. If the piecewise-defined function f is defined by

find each of the following values.

(a)

(b) f(−1)

(c)

(d)

(e) (5.72)

(f) f(π)

6. What is the y-intercept of the graph of the function f in Problem 5?

7. Determine the values of x for which the piecewise-defined function

is equal to the given number.

(a) 7

(b) 0

(c) -1

(d) -2

(e) 1

(f) -7

8. Determine the values of x for which the piecewise-defined function

is equal to the given number.

(a) 1

(b) 0

(c) 4

(d)

(e) 2

(f) - 4

In Problems 9–34, sketch the graph of the given piecewise-defined function. Find any x- and y-intercepts of the graph. Give any numbers at which the function is discontinuous.

9.

10.

11.

12.

13. y = [x + 2]

14. y = 2 + [x]

15. y = − [x]

16. y = [−x]

17. y = | x + 3|

18. y = − | x − 4|

19. y = 2 − | x |

20. y = − 1 − | x|

21. y = − 2 − |x + 1|

22.

23. y = − |5 − 3x |

24. y = |2x − 5|

25. y = |x² − 1|

26. y = |4 − x² |

27. y = | x² − 2x |

28. y = | −x² − 4x + 5|

29. y = ||x| − 2|

30.

31. y = |x³ − 1|

32. y = |[x]|

33.

34.

35. Without graphing, give the range of the function f(x) = (−1)^[x].

36. Compare the graphs of y = 2[x] and y = [2x].

In Problems 37–40, find a piecewise-defined formula for the function f whose graph is given. Assume that the domain of f is (− ∞, ∞).

37.

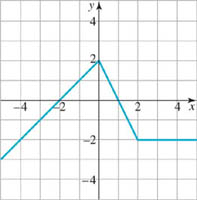
FIGURE 2.5.9 Graph for Problem 37

38.

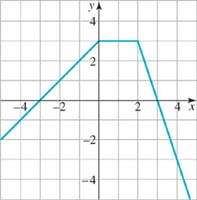
FIGURE 2.5.10 Graph for Problem 38

39.

FIGURE 2.5.11 Graph for Problem 39

40.

FIGURE 2.5.12 Graph for Problem 40

In Problems 41 and 42, sketch the graph of y = |f(x) |.

41. f is the function whose graph is given in Figure 2.5.9.

42. f is the function whose graph is given in Figure 2.5.10.

In Problems 43 and 44, use the definition of absolute value and express the given function f as a piecewise-defined function.

43.

44.

In Problems 45 and 46, find the value of the constant k such that the given piecewise-defined function f is continuous at x = 2. That is, the graph of f has no holes, gaps, or breaks in its graph at x = 2.

45.

46.

47. The ceiling function g(x) = [x] is defined to be the least integer n that is greater than or equal to x. Fill in the blanks.

48. Graph the ceiling function g(x) = [x] defined in Problem 47.

For Discussion

In Problems 49–52, describe in words how the graphs of the given functions differ. [Hint: Factor and cancel.]

49.

50.

51.

52.

53. Using the notion of a reflection of a graph in an axis, express the ceiling function g(x) = [x] in terms of the floor function f(x) = [x] (see page 86).

54. Discuss how to graph the function y = |x| + |x − 3|. Carry out your ideas.

2.6 Combining Functions

Introduction Two functions f and g can be combined in several ways to create new functions. In this section we will examine two such ways in which functions can be combined: through arithmetic operations, and through the operation of function composition.

Arithmetic Combinations Two functions can be combined through the familiar four arithmetic operations of addition, subtraction, multiplication, and division.

EXAMPLE 1 Sum, Difference, Product, and Quotient

Consider the functions f(x) = x² + 4x and g(x) = x² − 9. From (1)–(4) we can produce four new functions:

Domain of an Arithmetic Combination When combining two functions arithmetically it is necessary that both f and g be defined at a same number x. Hence the domain of the functions f + g, f − g, and fg is the set of real numbers that are common to both domains, that is, the domain is the intersection of the domain of f with the domain of g. In the case of the quotient f/g, the domain is also the intersection of the two domains, but we must also exclude any values of x for which the denominator g(x) is zero. In Example 1 the domain of f and the domain of g is the set of real numbers (−∞, ∞), and so the domain of f + g, f − g, and fg is also (−∞, ∞). However, since g(−3) = 0 and g(3) = 0, the domain of the quotient (f/g)(x) is (− ∞, ∞) with x = 3 and x = −3 excluded, in other words, (− ∞, −3) ∪ (−3, 3) ∪ (3, ∞). In summary, if the domain of is the set X₁ and the domain of g is the set X₂ then:

• the domain of f + g, f − g, and fg is X₁ ∩ X₂, and
• the domain of f/g is the set{x|x ∈. X₁ ∩ X₂, g(x) ≠ 0}.

EXAMPLE 2 Domain of f + g

By solving the inequality 1 − x ≥ 0, it is seen that the domain of is the interval (−∞, 1]. Similarly, the domain of the function is the interval [−2, ∞). Hence, the domain of the sum is the intersection (−∞, 1] ∩ [−2, ∞).You should verify this result by sketching these intervals on the number line that this intersection, or the set of numbers common to both domains, is the closed interval [−2, 1].

Composition of Functions Another method of combining functions f and g is called function composition. To illustrate the idea, let’s suppose that for a given x in the domain of g the function value g(x) is a number in the domain of the function f. This means we are able to evaluate f at g(x), in other words, f(g(x)). For example, suppose f(x) = x² and g(x) = x + 2. Then for x = 1, g(1) = 3, and since 3 is the domain of f, we can write f(g(1)) = f(3) = 3² = 9. Indeed, for these two particular functions it turns out that we can evaluate f at any function value g(x), that is,

The resulting function, called the composition of f and g, is defined next.

When computing a composition such as (f ° g) (x) = f(g(x)), be sure to substitute g(x) for every x that appears in f(x). See part (a) of the next example.

EXAMPLE 3 Two Compositions

If f(x) = x² + 3x −1 and g(x) = 2x² + 1, find (a) (f ° g)(x) and (b) (g ° f)(x).

Solution

(a) For emphasis we replace x by the set of parentheses () and write f in the form

.

Thus to evaluate (f ° g) (x) we fill each set of parentheses with g(x). We find

(b) In this case write g in the form

Then

Parts (a) and (b) of Example 3 illustrate that function composition is not commutative. That is, in general

.

The next example shows that a function can be composed with itself.

EXAMPLE 4 Composed with

If f(x) = 5x − 1, then the composition f ° f is given by

EXAMPLE 5 Writing a Function as a Composition

Express as the composition of two functions f and g.

Solution If we define f and g as xand g(x) = 6x³ + 8, then

There are other solutions to Example 5. For instance, if the functions f and g are defined by and g(x) = x³, then observe .

Domain of a Composition As stated in the introductory example to this discussion, to evaluate the composition (f ° g)(x) = f(g(x)) the number g(x) must be in the domain of f. For example, the domain is x ≥ 0, and the domain of g(x) = x − 2 is the set of real numbers (− ∞, ∞). Observe that we cannot evaluate f(g(1)) because g(1) = − 1 and − 1 is not in the domain of f. In order to substitute g(x) into f(x), g(x) must satisfy the inequality that defines the domain of f, namely, g(x) > 0. This last inequality is the same as x − 2 ≥ 0 or x ≥ 2. The domain of the composition is [2, ∞), which is only a portion of the original domain (−∞, ∞) of g. In general,

•    the domain of the composition f ° g consists of the numbers x in the domain of g such that g(x) is in the domain of f.

Read this sentence several times.

EXAMPLE 6 Domain of a Composition

Consider the function . From the requirement that x − 3 ≥ 0 we see that whatever number x is substituted into f must satisfy x ≥ 3. Now suppose g(x) = x² + 2 and we want to evaluate f(g(x)). Although the domain of g is the set of all real numbers, in order to substitute g(x) into f(x) we require that x be a number in that domain so that g(x) ≥ 3. From FIGURE 2.6.1 we see that the last inequality is satisfied whenever x ≤ −1 or x ≥ 1. In other words, the domain of the composition

is(−∞, −1] ∪ [1, ∞).

FIGURE 2.6.1 Domain of (f ° g)(x) in Example 6

In certain applications a quantity y is given as a function of a variable x which in turn is a function of another variable t. By means of function composition we can express y as a function of t. The next example illustrates the idea; the symbol V plays the part of y and r plays the part of x.

EXAMPLE 7 Inflating a Balloon

A weather balloon is being inflated with a gas. If the radius of the balloon is increasing at a rate of 5 cm/s, express the volume of the balloon as a function of time t in seconds.

Solution Let’s assume that as the balloon is inflated, its shape is that of a sphere. If r denotes the radius of the balloon, then r(t) = 5t. Since the volume of a sphere is , the composition is (V ° r)(t) = V(r(t)) = V(5t) or

Postscript The rigid and nonrigid transformations that were studied in Section 2.2 are examples of the operations on functions just discussed. For c > 0 a constant, the rigid transformations defined by y = f(x) + c and y = f(x) − c are the sum and difference of the function f(x) and the constant function g(x) = c. The nonrigid transformation y = cf(x) is the product of f(x) and the constant function g(x) = c. The rigid transformations defined by y = f(x + c) and y = f(x − c) are compositions of f(x) with the linear functions g(x) = x + c and g(x) = x − c, respectively.

2.6 Exercises
Answers to selected odd-numbered problems begin on page ANS–7.

In Problems 1–8, find the functions f + g, f − g, fg, and f/g, and give their domains.

1. f(x) = x ² + 1, g(x) = 2 x ² − x

2. f(x) = x ² − 4, g(x) = x + 3

3.

4.

5. f(x) = 3 x ³ − 4 x ² + 5 x, g(x) = (1 − x)2

6.

7.

8.

9. Fill in the table.

10. Fill in the table where g is an odd function.

In Problems 11–14, find the functions f ° g and g ° f and give their domains.

11.

12. f(x) = x² − x + 5, g(x) = −x + 4

13.

14.

In Problems 15–20, find the functions f ° g and g ° f.

15.

16. f(x) = x - 1, g(x) = x³

17.

18.

19.

20.

In Problems 21–24, find f ° f and f ° (1/f).

21. f(x) = 2x + 6

22. f(x) = x² + 1

23.

24.

In Problems 25 and 26, find (f ° g ° h)(x) = f(g(h(x))).

25.

26. f(x) = x², g(x) = x² + 3x, h(x) = 2x

27. For the functions f(x) = 2x + 7, g(x) = 3x², find (f ° g ° g)(x).

28. For the functions f(x) = −x + 5, g(x) = −4x² + x, find (f ° g ° f)(x).

In Problems 29 and 30, find (f ° f ° f)(x) = f(f(f(x))).

29. f(x) = 2x − 5

30. f(x) = x² − 1

In Problems 31–34, find functions f and g such that F(x) = f ° g.

31. F(x) = (x² − 4x) ⁵

32.

33.

34. F(x) = 1 + | 2x + 9 |

In Problems 35 and 36, sketch the graphs of the compositions f ° g and g ° f.

35. f(x) = |x| − 2, g(x) = |x − 2|

36.f(x) = [x − 1], g(x) = |x|

37. Consider the function y = f(x) + g(x), where f(x) = x and g(x) = − [x]. Fill in the blanks and then sketch the graph of the sum f + g on the indicated intervals.

38. Consider the function y = f(x) + g(x), where f(x) = |x| and g(x) = [x]. Proceed as in Problem 37 and then sketch the graph of the sum f + g.

In Problems 39 and 40, sketch the graph of the sum f + g.

39. f(x) = |x − 1|, g(x) = |x|

40. f(x) = x, g(x) = |x|

In Problems 41 and 42, sketch the graph of the product fg.

41. f(x) = x, g(x) = |x|

42. f(x) = x, g(x) = [x]

In Problems 43 and 44, sketch the graph of the reciprocal 1/f.

43. f(x) = |x|

44. f(x) = x − 3

Miscellaneous Calculus-Related Problems

In Problems 45 and 46,

(a) find the points of intersection of the graphs of the given functions,

(b) find the vertical distance d between the graphs on the interval I determined by the x-coordinates of their points of intersection,

(c) use the concept of a vertex of a parabola to find the maximum value of d on the interval I.

45.

FIGURE 2.6.2 Graph for Problem 45

46.

FIGURE 2.6.3 Graph for Problem 46

Miscellaneous Applications

47. For the Birds A birdwatcher sights a bird 100 ft due east of her position. If the bird is flying due south at a rate of 500 ft/min, express the distance d from the birdwatcher to the bird as a function of time t. Find the distance 5 minutes after the sighting. See FIGURE 2.6.4.

FIGURE 2.6.4 Birdwatcher in Problem 47

48. Bacteria A certain bacteria when cultured grows in a circular shape. The radius of the circle, measured in centimeters, is given by

where time t is measured in hours.

(a) Express the area covered by the bacteria as a function of time t.

(b) Express the circumference of the area covered as a function of time t.

For Discussion

49. Suppose f(x) = x² + 1and . Discuss: Why is the domain of

not (−∞, ∞)?

50. Suppose . Discuss: Why is the domain of

not{x|x ≠ 2}?

51. Find the error in the following reasoning: If f(x)=1/(x-2) and , then

52. Suppose 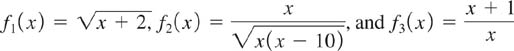. What is the domain of the function y = f₁(x) + f₂(x) + f₃(x)?

53. Suppose f(x) = x³ + 4x, g(x) = x − 2, and h(x) = −x. Discuss:Without actually graphing, how are the graphs of f °g, g ° f, f ° h, and h ° f related to the graph of f?

54. The domain of each piecewise-defined function,

is (− ∞, ∞). Discuss how to find f + g, f − g, and fg. Carry out your ideas.

55. Discuss how the graph of is related to the graph of y = f(x). Illustrate your ideas using f(x) = x² − 6x + 5.

56. Discuss:

(a) Is the sum of two even functions f and g even?

(b) Is the sum of two odd functions f and g odd?

(c) Is the product of an even function f with an odd function g even, odd, or neither?

(d) Is the product of an odd function f with an odd function g even, odd, or neither?

57. The product fg of two linear functions with real coefficients, f(x) = ax + b and g(x) = cx + d, is a quadratic function. Discuss: Why must the graph of this quadratic function have at least one x-intercept?

58. Make up two different functions f and g so that the domain of F(x) = f ° g is [−2, 0) ∪ (0, 2].

2.7 Inverse Functions

Introduction Recall that a function f is a rule of correspondence that assigns to each value x in its domain X, a single or unique value y in its range. This rule does not preclude having the same number y associated with several different values of x. For example, for f(x) = x² + 1, the value y = 5 occurs at either x = −2 or x = 2. On the other hand, for the function g(x) = x³, the value y = 64 occurs only at x = 4. Indeed, for every value y in the range of g (x) = x³, there corresponds only one value of x in the domain. Functions of this last kind are given a special name.

Horizontal Line Test Interpreted geometrically, this means that a horizontal line (y = constant) can intersect the graph of a one-to-one function in at most one point. Furthermore, if every horizontal line that intersects the graph of a function does so in at most one point, then the function is necessarily one-to-one. A function is not one-to-one if some horizontal line intersects its graph more than once.

EXAMPLE 1 Horizontal Line Test

The graphs of the functions f(x) = x² + 1and g(x) = x³, and a horizontal line y = c intersecting the graphs of f and g, are shown in FIGURE 2.7.1. Figure 2.7.1(a) indicates that there are two numbers x₁ and x₂ in the domain of f for which f(x₁) = f(x₂) = c. Inspection of Figure 2.7.1(b) shows that for every horizontal line y = c intersecting the graph, there is only one number x₁ in the domain of g such that g(x₁) = c. Hence the function f is not one-to-one, whereas the function g is one-to-one.

FIGURE 2.7.1 Two types of functions in Example 1

A one-to-one function can be defined in several different ways. Based on the preceding discussion, the following statement should make sense.

Stated in a negative way, (1) indicates that a function f is not one-to-one if different numbers x₁ and x₂(that is, x₁ ≠ x₂)can be found in the domain of f such that f(x₁) = f(x₂). You will see this formulation of the one-to-one concept when we solve certain kinds of equations in Chapter 5.

Consider (1) as a way of determining whether a function f is one-to-one without the benefit of a graph.

EXAMPLE 2 Checking for One-to-One

(a) Consider the function f(x) = x⁴ − 8x + 6. Now 0 ≠ 2 but observe that f(0) = f(2) = 6. Therefore f is not one-to-one.

(b) Consider the function , and let x₁ and x₂ be numbers in the domain of f. If we assume f(x₁) = f(x₂), that is, , then by taking the reciprocal of both sides we see

We conclude from (1) that f is one-to-one.

Inverse of a One-to-One Function Suppose f is a one-to-one function with domain X and range Y. Since every number y in Y corresponds to precisely one number x in X, the function f must actually determine a “reverse” function f⁻¹ whose domain is Y and range is X. As shown in FIGURE 2.7.2, f and f⁻¹ must satisfy

The equations in (2) are actually the compositions of the functions f and f⁻¹:

The function f⁻¹ is called the inverse of f or the inverse function for f. Following the convention that each domain element be denoted by the symbol x, the first equation in (3) is rewritten as f(f⁻¹(x)) = x. We summarize the results in (3).

Note of Caution: The symbol f⁻¹ does not mean the reciprocal 1/f. The number −1 is not an exponent.

FIGURE 2.7.2 Functions f and f⁻¹

Of course, if a function f is not one-to-one, then it has no inverse function.

EXAMPLE 3 Verifying an Inverse

Verify that the inverse of the one-to-one function .

Solution First observe that the domain and range of both functions is the entire set of real numbers (−∞, ∞). Now we can use (4) and (5).

First from (4) we see that

for every real number x. Similarly, from (5)

for every real number x. This shows that g = f ⁻¹

Properties Before we actually examine methods for finding the inverse of a one-to-one function f, let’s list some important properties about f and its inverse f^-1.

First Method for Finding f ⁻¹ We will consider two ways of finding the inverse of a one-to-one function f. Both methods require that you solve an equation; the first method begins with (4).

EXAMPLE 4 Inverse of a Function

(a) Find the inverse of . (b) Find the domain and range of f ⁻¹. Find the range of f.

Solution

(a) We proved in part (b) of Example 2 that f is one-to-one. To find the inverse of f using (4), we must substitute f ⁻¹(x) wherever x appears in f and then set the expression f(f ⁻¹(x)) equal to x:

By taking the reciprocal of both sides of the equation in the outline box we get,

Dividing both sides of the last equation by 2 yields the inverse of f:

(b) Inspection of f reveals that its domain is the set of real numbers except , that is, . Moreover, from the inverse just found we see that the domain of f ⁻¹ is {x | x ≠ 0}. Because range of f ⁻¹ = domain of f we then know that the range of f ⁻¹ is . From domain of f ⁻¹ = range of f we have also discovered that the range of f is {y | y ≠ 0}.

Second Method for Finding f ⁻¹ The inverse of a function f can be found in a different manner. If f ⁻¹ is the inverse of f, then x = f ⁻¹(y). Thus we need only do the following two things:

• Solve y = f(x) for the symbol x in terms of y (if possible). This gives x = f ⁻¹(y).

• Relabel the variable x as y and the variable y as x. This gives y = f ⁻¹(x).

EXAMPLE 5 Inverse of a Function

Find the inverse of f(x) = x³.

Solution In Example 1 we saw that this function was one-to-one. To begin, we rewrite the function as y = x³. Solving for x then gives x = y^1/3. Next we relabel variables to obtain y = x^1/3. Thus f ⁻¹(x) = x^1/3 or equivalently .

Finding the inverse of a one-to-one function y = f(x) is sometimes difficult and at times impossible. For example, it can be shown that the function f(x) = x³ + x + 3 is one-to-one and so has an inverse f ⁻¹, but solving the equation y = x³ + x + 3 for x is difficult for everyone (including your instructor). Nevertheless since f only involves positive integer powers of x, its domain is (−∞, ∞). If you investigate f graphically you are led to the fact that the range of f is also (− ∞, ∞). Consequently the domain and range of f ⁻¹ are (− ∞, ∞). Even though we don’t know f ⁻¹ explicitly it makes complete sense to talk about values such as f ⁻¹ (3) and f ⁻¹(5). In the case of f ⁻¹ (3) note that f(0) = 3. This means that f ⁻¹(3) = 0. Can you figure out the value of f ⁻¹(5)?

Graphs of f and f ⁻¹ Suppose that (a, b) represents any point on the graph of a one-to-one function f. Then f(a) = b and

implies that (b, a) is apointon the graph of f ⁻¹. As shownin FIGURE 2.7.3(a), the points (a, b) and (b, a) are reflections of each other in the line y = x. This means that the line y = x is the perpendicular bisector of the line segment from (a, b) to (b, a). Because each point on one graph is the reflection of a corresponding point on the other graph, we see in Figure 2.7.3(b) that the graphs of f ⁻¹ and f are reflections of each other in the line y = x. We also say that the graphs of f ⁻¹ and f are symmetric with respect to the line y = x.

FIGURE 2.7.3 Graphs of f and f⁻¹ are reflections in the line y = x.

EXAMPLE 6 Graphs of f and f⁻¹

In Example 5 we saw that the inverse of y = x³ is y = x^1/3. In FIGURES 2.7.4(a) and 2.7.4(b) we show the graphs of these functions; in Figure 2.7.4(c) the graphs are superimposed on the same coordinate system to illustrate that the graphs are reflections of each other in the line y = x.

FIGURE 2.7.4 Graphs of f and f ⁻¹ in Example 6

Every linear function f(x) = ax + b, a + 0, is one-to-one.

EXAMPLE 7 Inverse of a Function

Find the inverse of the linear function f(x) = 5x − 7.

Solution Since the graph of y = 5x − 7 is a nonhorizontal line, it follows from the horizontal line test that f is a one-to-one function. To find f ⁻¹ solve y = 5x − 7 for x:

Relabeling variables in the last equation gives . Therefore . The graphs of f and f ⁻¹ are compared in FIGURE 2.7.5.

Every quadratic function f(x) = ax² + bx + c, a ≠ 0, is not one-to-one.

FIGURE 2.7.5 Graphs of f and f⁻¹ in Example 7

Restricted Domains For a function f that is not one-to-one, it may be possible to restrict its domain in such a manner so that the new function consisting of f defined on this restricted domain is one-to-one and so has an inverse. In most cases we want to restrict the domain so that the new function retains its original range. The next example illustrates this concept.

EXAMPLE 8 Restricted Domain

In Example 1 we showed graphically that the quadratic function f(x) = x² + 1 is not one-to-one. The domain of f is (− ∞, ∞), and as seen in FIGURE 2.7.6(a), the range of f is [1, ∞). Now by defining f(x) = x² + 1 only on the interval [0, ∞), we see two things in Figure 2.7.6(b): the range of f is preserved and f(x) = x² + 1 confined to the domain [0, ∞) passes the horizontal line test, in other words, is one-to-one. The inverse of this new one-to-one function is obtained in the usual manner. Solving y = x² + 1 implies

The appropriate algebraic sign in the last equation is determined from the fact that the domain and range of f ⁻¹ are [1, ∞) and [0, ∞), respectively. This forces us to choose as the inverse of f. See Figure 2.7.6(c).

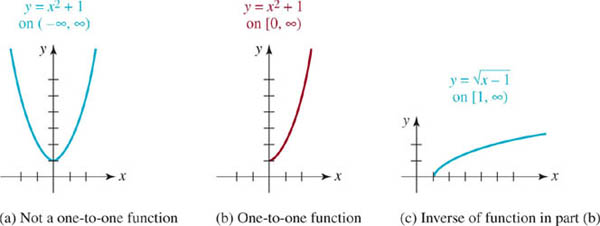
FIGURE 2.7.6 Inverse function in Example 8

2.7 Exercises
Answers to selected odd-numbered problems begin on page ANS–7.

In Problems 1–6, the graph of a function f is given. Use the horizontal line test to determine whether f is one-to-one.

1.

FIGURE 2.7.7 Graph for Problem 1

2.

FIGURE 2.7.8 Graph for Problem 2

3.

FIGURE 2.7.9 Graph for Problem 3

4.

FIGURE 2.7.10 Graph for Problem 4

5.

FIGURE 2.7.11 Graph for Problem 5

6.

FIGURE 2.7.12 Graph for Problem 6

In Problems 7–10, sketch the graph of the given piecewise-defined function f to determine whether it is one-to-one.

7.

8.

9.

10.

In Problems 11–14, proceed as in Example 2(a) to show that the given function f is not one-to-one.

11. f(x) = x² − 6x

12. f(x) = (x − 2)(x + 1)

13.

14. f(x) = |x + 10|

In Problems 15-18, proceed as in Example 2(b) to show that the given function f is one-to-one.

15.

16.

17.

18.

In Problems 19–24, proceed as in Example 3 and verify that the inverse of the one-to-one function f is the function g by showing f(g(x)) = x and g(f(x)) = x.

19. f(x) = x + 5; g(x) = x − 5

20.

21.

22.

23.

24.

In Problems 25 and 26, the given function f is one-to-one. Without finding f⁻¹ find its domain and range.

25.

26.

In Problems 27 and 28, the given function f is one-to-one. The domain and range of f is given. Find f ⁻¹ and give its domain and range.

27.

28.

In Problems 29–34, the given function f is one-to-one. Find f ⁻¹. Sketch the graph of f and f ⁻¹ on the same coordinate axes.

29. f(x) = −2x + 6

30. f(x) = −2x + 1

31. f(x) = x³ + 2

32. f(x) = 1 − x³

33.

34.

In Problems 35–38, the given function f is one-to-one. Find f ⁻¹. Proceed as in Example 4(b) and find the domain and range of f^–1. Then find the range of f.

35.

36.

37.

38.

In Problems 39–42, the given function f is one-to-one. Without finding f ⁻¹, find the point on the graph of f ⁻¹ corresponding to the indicated value of x in the domain of f.

39. f(x) = 2x³ + 2x; x = 2

40. f(x) = 8x - 3; x = 5

41.

42.

In Problems 43 and 44, sketch the graph of f ⁻¹ from the graph of f ¹.

43.

FIGURE 2.7.13 Graph for Problem 43

44.

FIGURE 2.7.14 Graph for Problem 44

In Problems 45 and 46, sketch the graph of f from the graph of f ⁻¹.

45.

FIGURE 2.7.15 Graph for Problem 45

46.

FIGURE 2.7.16 Graph for Problem 46

In Problems 47-50, the function f is not one-to-one on the given domain but is one-to-one on the restricted domain (the second interval). Find the inverse of the one-to-one function and give its domain. Sketch the graph of f on the restricted domain and the graph of f ⁻¹ on the same coordinate axes.

47. f(x) = 4x² + 2, (− ∞, ∞); [0, ∞)

48.

49.

50.

In Problems 51and 52, verify that f(f ⁻¹(x)) = x and f ⁻¹ (f(x)) = x.

51.

52.

Discussion Problems

53. Suppose f is a continuous function that is increasing (or decreasing) for all x in its domain. Explain why f is necessarily one-to-one.

54. Explain why the graph of a one-to-one function f can have at most one x-intercept.

55. The function f(x) = |2x − 4| is not one-to-one. How should the domain of f be restricted so that the new function has an inverse? Find f ⁻¹ and give its domain and range. Sketch the graph of f on the restricted domain and the graph of f ⁻¹ on the same coordinate axes.

56. What property do the one-to-one functions y = f(x) shown in FIGURES 2.7.17(a) and 2.7.17(b) have in common? Find two more explicit functions with this same property. Be very explicit about what this property has to do with f ⁻¹.

FIGURE 2.7.17 Graphs for Problem 56

2.8 Building a Function from Words

Introduction In calculus there will be several instances when you will be expected to translate the words that describe a problem into mathematical symbols and then set up or construct either an equation or a function.

In this section we focus on problems that involve functions. We begin with a verbal description about the product of two numbers.

EXAMPLE 1 Product of Two Numbers

The sum of two nonnegative numbers is 15. Express the product of one and the square of the other as a function of one of the numbers.

Solution We first represent the two numbers by the symbols x and y and recall that “nonnegative” means that x ≥ 0 and y ≥ 0. The first sentence then says that x + y = 15; this is not the function we are seeking. The second sentence describes the function we want; it is called “the product.” Let’s denote “the product” by the symbol P. Now P is the product of one of the numbers, say, x and the square of the other, that is, y²:

No, we are not finished because P is supposed to be a “function of one of the numbers.” We now use the fact that the numbers x and y are related by x + y = 15. From this last equation we substitute y = 15 − x into (1) to obtain the desired result:

Here is a symbolic summary of the analysis of the problem given in Example 1:

Notice that the second sentence is vague about which number is squared. This means that it really doesn’t matter; (1) could also be written as P = yx². Also, we could have used x = 15 − y in (1) to arrive at P(y) = (15 − y)y². In a calculus setting it would not have mattered whether we worked with P(x) or with P(y) because by finding one of the numbers we automatically find the other from the equation x + y = 15. This last equation is commonly called a constraint. A constraint not only defines the relationship between the variables x and y but often puts a limitation on how x and y can vary. As we see in the next example, the constraint helps in determining the domain of the function that you have just constructed.

EXAMPLE 2 Example 1 Continued

What is the domain of the function P(x) in (2)?

Solution Taken out of the context of the statement of the problem in Example 1, one would have to conclude from the discussion on page 50 of Section 2.1 that the domain of

is the set of real numbers (− ∞, ∞). But in the context of the original problem, the numbers were to be nonnegative. From the requirement that x ≥ 0 and y = 15 − x ≥ 0 we get x ≥ 0 and x ≤ 15, which means that x must satisfy the simultaneous inequality 0 ≤ x ≤ 15. Using interval notation, the domain of the product function P in (2) is the closed interval [0, 15].

Another way of looking at the conclusion of Example 2 is this: The constraint x + y = 15 dictates that y = 15 − x. Thus if x were allowed to be larger than 15 (say, x = 17.5), then y = 15 − x would be a negative number, which contradicts the initial assumption that y ≥ 0.

Optimization Problems For the remainder of this section we are going to examine “word problems” taken directly from a calculus text. These problems, variously called “optimization problems” or “applied maximum and minimum problems,” consist of two parts, the “precalculus part” where you set up the function to be optimized and the “calculus part” where you perform calculus-specific operations on the function that you have just found to find its maximum or minimum value. The calculus part is usually identifiable by words such as “maximum (or minimum),” “least,” “greatest,” “large as possible,” “find the dimensions,” and so on. For example, the actual statement of Example 1 as it appears in a calculus text is:

Find two nonnegative numbers whose sum is 15 such that the product of one and the square of the other is a maximum.

The big hurdle for many students is separating out the words that define the function to be optimized from all the words contained in the statement of the problem.

Before proceeding with the examples, you are encouraged to read the Notes from the Classroom at the end of this section.

The next example describes a geometric problem that asks for a “largest rectangle.” Remember, you are not expected to work the entire problem by trying to actually find the “largest rectangle,” which you would do in a calculus course. Right now your only job is to pick out the words, as we illustrated in (3), that tell you what the function is and then construct it using the variables introduced. In calculus, the function to be optimized is called the objective function.

Please note.

EXAMPLE 3 Largest Rectangle

Find the objective function in the following calculus problem:

A rectangle has two vertices on the x-axis and two vertices on the semicircle whose equation . See FIGURE 2.8.1(a). Find the dimensions of 'the largest rectangle.

FIGURE 2.8.1 Rectangle in Example 3

Solution In calculus the words “largest rectangle” mean that we are seeking the rectangle, of the many that can be drawn in the semicircle, that has the greatest or maximum area. Hence, the function we must construct is the area A of the rectangle. If (x, y), x > 0, y > 0, denotes the vertex of the rectangle on the circle in the first quadrant, then as shown in Figure 2.8.1(b) the area A is length × width, or

The constraint in this problem is the equation of the semicircle. We use the constraint equation to eliminate y in (4) and obtain the area of the rectangle or the objective function,

This ends the “precalculus part” of the problem.

The next step would be calculus procedures to determine the value of x for which the objective function A(x) takes on its largest value.

Were we again to consider the function A(x) out of the context of the problem in Example 3, its domain would be [−5, 5]. Because we assumed that x > 0 the domain of A(x) in (4) is actually the open interval (0, 5). But in calculus we would use the closed interval [0, 5] even though when x = 0 and x = 5 the area would be A(0) = 0 and A(5) = 0, respectively. Do not worry about this last technicality.

EXAMPLE 4 Least Amount of Fencing

Find the objective function in the following calculus problem:

A rancher intends to mark off a rectangular plot of land that will have an area of 1000 m². The plot will be fenced and divided into two equal portions by an additional fence parallel to two sides. Find the dimensions of the land that require the least amount of fence.

Solution Your drawing should be a rectangle with a line drawn down its middle, similar to that given in FIGURE 2.8.2. As shown in the figure, let x > 0 be the length of the rectangular plot of land and let y > 0 denote its width. The function we seek is the “amount of fence.” If the symbol F represents this amount, then the sum of the lengths of the five portions—two horizontal and three vertical—of the fence is

FIGURE 2.8.2 Rectangular plot of land in Example 4

But the fenced-in land is to have an area of 1000 m², and so x and y must be related by the constraint xy = 1000. From the last equation we get y = 1000/x which can be used to eliminate y in (6). Thus, the amount of fence F as a function of x is

Since x represents a physical dimension that satisfies xy = 1000, we conclude that it is positive. But other than that, there is no restriction on x. Thus, unlike the previous example, the objective function (7) is not defined on a closed interval. The domain of F(x) is (0, ∞).

As can be seen from the graph of (7) given in FIGURE 2.8.3, F has a minimum at some value of x, say x = c. With a graphing calculator or computer we can approximate c and F(c), but with calculus we can find their exact values.

FIGURE 2.8.3 In Example 4, F(c) is the smallest value of F for x > 0

If a problem involves triangles, you should study the problem carefully and determine whether the Pythagorean theorem, similar triangles, or trigonometry is applicable.

EXAMPLE 5 Shortest Ladder

Find the objective function in the following calculus problem:

A 10-ft wall stands 5 ft from a building. Find the length of the shortest ladder, supported by the wall, that reaches from the ground to the building.

Solution The words “shortest ladder” indicate that we want a function that describes the length of the ladder. Let L denote this length. With x and y defined in FIGURE 2.8.4, we see that there are two right triangles, the larger triangle has three sides with lengths L, y, and x + 5, and the smaller triangle has two sides of lengths x and 10. Now the ladder is the hypotenuse of the larger right triangle, so by the Pythagorean theorem,

FIGURE 2.8.4 Ladder in Example 5

The right triangles in Figure 2.8.4 are similar because they both contain a right angle and share the common acute angle the ladder makes with the ground. We then use the fact that the ratios of corresponding sides of similar triangles are equal. This enables us to write

Using the last result, (8) becomes

Taking the square root gives us L as a function of x

The domain of the objective function L(x) is (0, ∞).

EXAMPLE 6 Closest Point

Find the objective function in the following calculus problem:

Find the point in the first quadrant on the circle x² + y² = 1 that is closest to the point (2, 4).

Solution Let (x, y) denote the point in the first quadrant on the circle closest to (2, 4) and let d represent the distance from (x, y) to (2, 4). See FIGURE 2.8.5. Then from the distance formula, (2) of Section 1.3,

FIGURE 2.8.5 Distance d in Example 6

The constraint in this problem is the equation of the circle x² + y² = 1. From this we can immediately replace x² + y² in (9) by the number 1. Moreover, using the constraint to write allows us to eliminate y in (9). Thus the distance d as a function of x is:

Since (x, y) is a point on the circle in the first quadrant the variable x can range from 0 to 1, that is, the domain of the objective function in (10) is the closed interval [0, 1 ].

NOTES FROM THE CLASSROOM

When we get to the sections in a calculus text devoted to word problems students often react with groans, ambivalence, and dismay. While not guaranteeing anything, the following suggestions might help you to get through the problems in Exercises 2.8.

• At least try to develop a positive attitude. Try to be neat and organized.
• Read the problem slowly. Then read the problem several more times.
• Pay attention to words such as “maximum,” “least,” “greatest,” and “closest” because they may provide a clue about the nature of the function you are seeking. For example, if a problem asks for “closest,” then the function you are seeking most probably involves distance; if a problem asks for “least material,” then the function you want may be surface area. See Problems 35 and 42 in Exercises 2.8.
• Whenever possible, sketch a curve or a picture and identify given quantities in your sketch. Keep your sketch simple.
• Introduce variables and note any constraint or relationship between the variables (such as x + y = 15 in Example 1).
• Identify the domain of the function just constructed. Keep in mind that if the problem mentions “dimensions” then the variables representing those quantities must be nonnegative.

2.8 Exercises
Answers to selected odd-numbered problems begin on page ANS–8.

In Problems 1–26, proceed as in Example 1 and translate the words into an appropriate function. Give the domain of the function.

1. The product of two positive numbers is 50. Express their sum as a function of one of the numbers.

2. Express the sum of a nonzero number and its reciprocal as a function of the number.

3. The sum of two nonnegative numbers is 1. Express the sum of the square of one and twice the square of the other as a function of one of the numbers.

4. Let m and n be positive integers. The sum of two nonnegative numbers is S. Express the product of the mth power of one and the nth power of the other as a function of one of the numbers.

5. A rectangle has a perimeter of 200 in. Express the area of the rectangle as a function of the length of one of its sides.

6. A rectangle has an area of 400 in². Express the perimeter of the rectangle as a function of the length of one of its sides.

7. Express the area of the rectangle shaded in FIGURE 2.8.6 as a function of x.

FIGURE 2.8.6 Rectangle in Problem 7

8. Express the length of the line segment containing the point (2, 4) shown in FIGURE 2.8.7 as a function of x.

FIGURE 2.8.7 Line segment in Problem 8

9. Express the distance from a point (x, y) on the graph of x + y = 1 to the point (2, 3) as a function of x.

10. Express the distance from a point (x, y) on the graph of y = 4 − x² to the point (0, 1) as a function of x.

11. Express the perimeter of a square as a function of its area A.

12. Express the area of a circle as a function of its diameter d.

13. Express the diameter of a circle as a function of its circumference C.

14. Express the volume of a cube as a function of the area A of its base.

15. Express the area of an equilateral triangle as a function of its height h.

16. Express the area of an equilateral triangle as a function of the length s of one of its sides.

17. A wire of length x is bent into the shape of a circle. Express the area of the circle as a function of x.

18. A wire of length L is cut x units from one end. One piece of the wire is bent into a square and the other piece is bent into a circle. Express the sum of the areas as a function of x.

19. A tree is planted 30 ft from the base of a street lamp that is 25 ft tall. Express the length of the tree’s shadow as a function of its height.

20. The frame of a kite consists of six pieces of lightweight plastic. The outer frame of the kite consists of four precut pieces, two pieces of length 2 ft, and two pieces of length 3 ft. Express the area of the kite as a function of x, where 2x is the length of the horizontal cross bar piece shown in FIGURE 2.8.8.

FIGURE 2.8.8 Kite in Problem 20

21. A company wants to construct an open rectangular box with a volume of 450 in³ so that the length of its base is 3 times its width. Express the surface area of the box as a function of the width.

22. A conical tank, with vertex down, has a radius of 5 ft and a height of 15 ft. Water is pumped into the tank. Express the volume of the water as a function of its depth. [Hint: The volume of a cone is . Although the tank is a three-dimensional object, examine it in cross section as a two-dimensional triangle.]

23. Car A passes point O heading east at a constant rate of 40 mi/h; car B passes the same point 1 hour later heading north at a constant rate of 60 mi/h. Express the distance between the cars as a function of time t, where t is measured starting when car B passes point O.

24. At time t = 0 (measured in hours), two airliners with a vertical separation of 1 mile pass each other going in opposite directions. If the planes are flying horizontally at rates of 500 mi/h and 550 mi/h, express the horizontal distance between them as a function of t. [Hint: distance = rate × time.]

25. The swimming pool shown in FIGURE 2.8.9 is 3 ft deep at the shallow end, 8 ft deep at the deepest end, 40 ft long, 30 ft wide, and the bottom is an inclined plane. Water is pumped into the pool. Express the volume of the water in the pool as a function of height h of the water above the deep end. [Hint: The volume will be a piecewise-defined function with domain 0 ≤ h ≤ 8.]

FIGURE 2.8.9 Swimming pool in Problem 25

26. USPS regulations for parcel post stipulate that the length plus girth (the perimeter of one end) of a package must not exceed 108 inches. Express the volume of the package as a function of the width x shown in FIGURE 2.8.10.

FIGURE 2.8.10 Package in Problem 26

In Problems 27–48, proceed as in Examples 3–5 and find the objective function for the given calculus problem. Give the domain of the objective function, but do not attempt to solve the problem.

27. Find a number that exceeds its square by the greatest amount.

28. Of all rectangles with perimeter 20 inches, find the one with the shortest diagonal.

29. A rectangular plot of land will be fenced into three equal portions by two dividing fences parallel to two sides. If the area to be enclosed is 4000 m², find the dimensions of the land that require the least amount of fence.

30. A rectangular plot of land will be fenced into three equal portions by two dividing fences parallel to two sides. If the total fence to be used is 8000 m, find the dimensions of the land that has the greatest area.

31. A rancher wishes to build a rectangular corral with an area of 128,000 ft² with one side along a straight river. The fencing along the river costs $1.50 per foot, whereas along the other three sides the fencing costs $2.50 per foot. Find the dimensions of the corral so that the cost of construction is a minimum. [Hint: Along the river the cost of x ft of fence is 1.50x]

32. A rectangular yard is to be enclosed with a fence by attaching it to a house whose length is 40 feet. See FIGURE 2.8.11. The amount of fencing to be used is 160 feet. Find the dimensions of the yard so that the greatest area is enclosed.

FIGURE 2.8.11 House and yard in Problem 32

33. Consider all rectangles that have the same perimeter p. (Here p represents a constant.) Of these rectangles, show that the one with the largest area is a square.

34. Find the vertices (x, 0) and (0, y) of the shaded triangular region in FIGURE 2.8.12 so that its area is a minimum.

FIGURE 2.8.12 Line segment in Problem 34

35. (a) An open rectangular box is to be constructed with a square base and a volume of 32,000 cm³. Find the dimensions of the box that require the least amount of material. See FIGURE 2.8.13.

(b) If the rectangular box in part (a) is closed, find the dimensions that require the least amount of material.

FIGURE 2.8.13 Box in Problem 35

36. A closed rectangular box is to be constructed with a square base. The material for the top costs $2 per square foot whereas the material for the remaining sides costs $1 per square foot. If the total cost to construct each box is $36, find the dimensions of the box of greatest volume that can be made.

37. A rain gutter with a rectangular cross section is made from a 1 ft × 20 ft piece of metal by bending up equal amounts from the 1-ft side. See FIGURE 2.8.14. How should the metal be bent up on each side in order to make the capacity of the gutter a maximum? [Hint: Capacity = volume.]

FIGURE 2.8.14 Rain gutter in Problem 37

38. A Norman window consists of a rectangle surmounted by a semicircle as shown in FIGURE 2.8.15. If the total perimeter of the window is 10 m, find the dimensions of the window with the largest area.

FIGURE 2.8.15 Norman window in Problem 38

39. A printed page will have 2-in. margins of white space on the sides and 1-in. margins of white space on the top and bottom. The area of the printed portion is 32 in². Determine the dimensions of the page so that the least amount of paper is used.

40. Find the dimensions of the right circular cylinder with greatest volume that can be inscribed in a right circular cone of radius 8 in. and height 12 in. See FIGURE 2.8.16.

FIGURE 2.8.16 Inscribed cylinder in Problem 40

41. Find the maximum length L of a thin board that can be carried horizontally around the right-angle corner shown in FIGURE 2.8.17. [Hint: Use similar triangles.]

FIGURE 2.8.17 Board in Problem 41

42. A juice can is to be made in the form of a right circular cylinder and have a volume of 32 in³. See FIGURE 2.8.18. Find the dimensions of the can so that the least amount of material is used in its construction. [Hint: Material = total surface area of can = area of top + area of bottom + area of lateral side. If the circular top and bottom covers are removed and the cylinder is cut straight up its side and flattened out, the result is the rectangle shown in Figure 2.8.18(c).]

FIGURE 2.8.18 Juice can in Problem 42

43. The lateral side of a cylinder is to be made from a rectangle of flimsy sheet plastic. Because the plastic material cannot support itself, a thin, stiff wire is embedded in the material as shown in FIGURE 2.8.19(a). Find the dimensions of the cylinder of largest volume that can be constructed if the wire has a fixed length L. [Hint: There are two constraints in this problem. In Figure 2.8.19(b), the circumference of a circular end of the cylinder is y.]

FIGURE 2.8.19 Cylinder in Problem 43

44. Many medications are packaged in capsules as shown in the accompanying photo. Assume that a capsule is formed by adjoining two hemispheres to the ends of a right circular cylinder as shown in FIGURE 2.8.20. If the total volume of the capsule is to be 0.007 in.³, find the dimensions of the capsule so that the least amount of material is used in its construction. [Hint: The volume of a sphere is and its surface area is 4πr².]

FIGURE 2.8.20 Model of a capsule in Problem 44

45. A 20-ft long water trough has ends in the form of isosceles triangles with sides that are 4 ft long. See FIGURE 2.8.21. Determine the dimension across the top of the triangular end so that the volume of the trough is a maximum. [Hint:A right cylinder is not necessarily a circular cylinder where the top and bottom are circles. The top and bottom of a right cylinder are the same but could be a triangle, a pentagon, a trapezoid, and so on. The volume of a right cylinder is the area of the base × the height.]

Capsule

FIGURE 2.8.21 Water trough in Problem 45

46. Some birds fly more slowly over water than over land. A bird flies at constant rates 6 km/h over water and 10 km/h over land. Use the information in FIGURE 2.8.22 to find the path the bird should take to minimize the total flying time between the shore of one island and its nest on the shore of another island. [Hint: distance = rate × time.]

FIGURE 2.8.22 The bird in Problem 46

47. In a race a woman is required to swim from a floating dock A to the beach and, without stopping, swim from the beach out to another floating dock C. The distances are shown in FIGURE 2.8.23. She estimates that she can swim from dock A to the beach at a constant rate of 3 mi/h and out from the beach to dock C at a rate of 2 mi/h. Where should she touch the beach in order to minimize the total swimming time from A to C?

FIGURE 2.8.23 Swimmer in Problem 47

48. Two flag poles are secured by wires that are attached at a single point between the poles. See FIGURE 2.8.24. Where should the point be located to minimize the total length of wire used?

FIGURE 2.8.24 Flag poles in Problem 48

For Discussion

49. In Problem 19, what happens to the length of the tree’s shadow as its height approaches 25 ft?

50. In an engineering text, the area of the octagon shown in FIGURE 2.8.25 is given as A = 3.31r². Show that this formula is actually an approximation to the area; that is, find the exact area A of the octagon as a function of r.

FIGURE 2.8.25 Octagon in Problem 50

2.9 The Tangent Line Problem

Introduction In a calculus course you will study many different things, but roughly, the subject “calculus” is divided into two broad but related areas known as differential calculus and integral calculus. The discussion of each of these topics invariably begins with a motivating problem involving the graph of a function. Differential calculus is motivated by the problem

Find a tangent line to the graph of a function f,

whereas integral calculus is motivated by the problem

Find the area under the graph of a function f.

The first problem will be addressed in this section; the second problem will be discussed in Section 3.7.

Tangent Line to a Graph The word tangent stems from the Latin verb tangere, meaning “to touch.” You might remember from the study of plane geometry that a tangent to a circle is a line L that intersects, or touches, the circle in exactly one point P. See FIGURE 2.9.1. It is not quite as easy to define a tangent line to the graph of a function f. The idea of touching carries over to the notion of a tangent line to the graph of a function, but the idea of intersecting the graph in one point does not carry over.*

FIGURE 2.9.1 Tangent line L touches a circle at point P

Suppose y = f(x) is a continuous function. If, as shown in FIGURE 2.9.2, f possesses a line L tangent to its graph at a point P, then what is the equation of this line? To answer this question, we need the coordinates of P and the slope m_tan of L. The coordinates of P pose no difficulty, since a point on the graph of a function f is obtained by specifying a value of x in the domain of f.The coordinates of the point of tangency at x = a are then(a, f(a)). As a means of approximating the slope m_tan, we can readily find the slopes m_sec of secant lines that pass through the point P and any other point Q on the graph. See FIGURE 2.9.3.

FIGURE 2.9.2 Tangent line L to a graph at point P

FIGURE 2.9.3 Slopes of secant lines approximate the slope m_tan of L

Slope of Secant Lines If P has coordinates (a, f(a)) and if Q has coordinates (a + h, f(a + h)), then as shown in FIGURE 2.9.4, the slope of the secant line through P and Q is

FIGURE 2.9.4 Secant lines swing into the tangent line L as h → 0

or

The expression on the right-hand side of the equality in (1) is called a difference quotient. When we let h take on values that are closer and closer to zero, that is, as h → 0, the sequence of points Q(a + h, f(a + h)) move along the curve closer and closer to the point P(a, f(a)). Intuitively, we expect the secant lines to approach the tangent line L, and that m_sec → m_tan as h → 0. Using the idea of a limit introduced in Section 1.5 we write , or equivalently from (1),

provided the limit exists. Just like the problems discussed in Section 1.5, observe that the limit in (2) has the indeterminate form 0/0 as h → 0.

We are not going to delve into any theoretical details about when the limit (2) exists or does not exist—that discussion properly belongs in a calculus course. So to simplify the discussion, we will drop the phase “provided the limit exists.” For this course it suffices simply to be aware of the fact that the limit (2) may not exist for certain values of a.

It is very likely that early on in your calculus course you will be asked to compute the limit of a difference quotient such as (2). The computation of (2) is essentially a four-step process, and three of these steps involve only precalculus mathematics: algebra and trigonometry. Getting over the hurdles of algebraic or trigonometric manipulations in these first three steps is your primary goal. If done accurately, the fourth step, or the calculus step, may be the easiest part of the problem. In preparation for calculus we recommend that you be able to carry out the calculation of (2) for functions involving

• positive integer powers of x such as xⁿ for n = 1,2, and 3,

• division of functions such as , and

• radicals such as .

See Problems 1–10 in Exercises 2.9.

review (a = b)ⁿ for n = 2 and 3

review adding symbolic fractions

review rationalization of numerators and denominators

EXAMPLE 1 The Four-Step Process

Find the slope of the tangent line to the graph of y = x² = 2 at x = 1.

Solution We first compute the difference quotient in (2) with the identification that a = 1.

(i) The initial step is the computation of f(a + h). Because functions can be complicated, it might help in this step to think of x wherever it appears in the function f (x) as a set of parentheses ( ). For the given function we write f( ) ⁼ ( )² = 2. The idea is to substitute 1 + h into those parentheses and carry out the required algebra:

(ii) The computation of the difference f(a + h) – f(a) is the most important step. It is imperative that you simplify this step as much as possible. Here is a tip: In many of the problems that you will be required to do in calculus you will be able to factor h from the difference f(a + h) – f(a). To begin, compute f(a), which in this case is f(1) = 1² + 2 = 3. Next, you can use the result from the preceding step:

(iii) The computation of the difference quotient is now straightforward. Again, we use the results from the preceding step:

(iv) The calculus step is now easy. From (2) we have

      The slope of the tangent line to the graph of y = x² + 2 at(1, 3)is 2.

EXAMPLE 2 Equation of Tangent Line

Find an equation of the tangent line whose slope was found in Example 1.

Solution We know a point (1, 3) and a slope m_tan = 2, and so from the point-slope equation of a line we find

Observe that the last equation is consistent with the x- and y-intercepts of the red line in FIGURE 2.9.5.

The Derivative As you inspect Figure 2.9.5, imagine tangent lines at various points on the graph of f(x) = x² + 2. This particular function is known to have a tangent line at every point on its graph. The tangent lines to the left of the origin have negative slope, the tangent line at (0, 2) has zero slope, and the tangent lines to the right of the origin have positive slope (as seen in Example 1). In other words, for a function f the value of m_tan at a point (a, f(a)) depends on the choice of the number a. Roughly speaking, there is at most one value of m_tan for each number a in the domain of a function f. More specifically, m_tan is itself a function with a domain that is a subset of the domain of the function f. Furthermore, it is usually possible to obtain a formula for this slope function. This is accomplished by computing the limit of the difference quotient as h → 0. We then substitute a value of x after the limit has been found. The slope function derived in this manner from f is said to be the derivative of f and (instead of m_tan) is denoted by the symbol f '.

FIGURE 2.9.5 Tangent line in Example 2

EXAMPLE 3 Example 1 Revisited

Compute the derivative of f(x) = x² + 2.

Solution We proceed exactly as in Example 1 except that we find f(x + h) instead of f (1 + h). In the first three steps we calculate the difference quotient; in steps (ii) and (iii) we use the results in the preceding step. In step (iv) we compute the limit of the difference quotient.

(iv) From (3) the derivative of f is the limit as h → 0 of the result in (iii). During the process of shrinking h smaller and smaller, x is held fixed. Hence

So now we have two functions; from f(x) = x² + 2 we have obtained the derivative f ' (x) = 2x. When evaluated at a number x, the function f gives the y-coordinate of a point on the graph and the derived function f ' gives the slope of the tangent line at that point. We have already seen in Example 1 that f(1) = 3 and f ' (1) = 2.

With the aid of the derivative f ' (x) = 2x we can find slopes at other points on the graph of f(x) = x² + 2. For example,

The fact that f '(0) = 0 means that the tangent line is horizontal at (0, 2).

EXAMPLE 4 Derivative of a Function

Compute the derivative of f(x) = 2x³ – 4x + 5.

Solution

(i ) The function is f( ) = 2( )³ – 4( ) + 5 and so

 The algebra here is a bit more complicated than in the previous example. We will use the binomial expansion for (a + b)³ and the distributive law. Continuing,

See (7) on page 36.

(ii) As mentioned previously, in this step we are looking for a factor of h:

(iii) We use the last result:

(iv) From (3) and the preceding step the derivative of f is

EXAMPLE 5 Equation of Tangent Line

Find an equation of the tangent line to the graph of f(x) = 2/x at x = 2.

Solution We start by finding the derivative of f. In the second of the four steps we will have to combine two symbolic fractions by means of a common denominator.

(iii) The last result is to be divided by h, or more precisely . We invert and multiply by :

(iv) From (3) the derivative of f is

We are now in a position to find an equation of the tangent line at the point corresponding to x = 2. From f(2) = 2/2 = 1, we get the point of tangency (2, 1). Then from the derivative f'(x) = –2/x² we see that f' (2) = –2/4, and so the slope of the tangent line at (2, 1) is From the point-slope equation of a line, the tangent line is

The graph of y = 2/x is the graph of y = 1/x stretched vertically. (See Figure 2.2.1(e).) The tangent line at (2, 1) is shown in red in FIGURE 2.9.6.

FIGURE 2.9.6 Tangent line in Example 5

Postscript There is an alternative definition of the derivative. If we let x = a + h in (2), then h = x – a.Consequently the slope of the secant line through P(a, f(a)) and Q(x, f(x)), as shown in FIGURE 2.9.7, is . As h → 0 we must have x → a, and so the derivative (3) takes on the form

EXAMPLE 6 Using (4)

Use (4) to compute the derivative of f(x) = 4x² − 5x + 9.

Solution We use the four-step process exactly as in Examples 3 and 4. The algebra is a slightly different; the analogue of the tip in (ii) of Example 1 is that we look for the factor x − a in the difference f(x) − f(a). Thus step (ii) will often require factoring the difference of two squares, the difference of two cubes, and so on.

FIGURE 2.9.7 Secant line and tangent line at (a, f(a))

Review (1) and (2) of Section 1.5.

(iii)

(iv) In the limit process indicated in (4), a is held fixed. Hence

As you can see in (4) and the final line in Example 6, the derivative comes out a function of the symbol a rather than x, that is, f'(a) = 8a − 5. As a consequence, (4) is not used as often as (3) to compute a derivative. See Problems 33–40 in Exercises 2.9. Nevertheless, (4) is important because it is convenient to use in some theoretical aspects of differential calculus.

2.9 Exercises
Answers to selected odd-numbered problems begin on page ANS–8.

In Problems 1–10, proceed as in Example 1.

(a) Compute the difference quotient at the given value of a.

(b) Then, if instructed, compute

(c) Use the result of part (b) to find an equation of the tangent line at the point of tangency.

1. f(x) = x² − 6, a = 3

2. f(x) = − 3x² + 10, a = −1

3. f(x) = x² − 3x, a = 1

4. f(x) = −x² + 5x − 3, a = − 2

5. f(x) = − 2x³ + x, a = 2

6.

7.

8.

9.

10.

In Problems 11–26, proceed as in Examples 3 and 4.

(a) Compute the difference quotient for the given function.

(b) Then, if instructed, compute the derivative

11. f(x) = 10

12. f(x) = − 3x + 8

13. f(x) = −4x²

14. f(x) = x² − x

15. f(x) = 3x² − x + 7

16. f(x) = 2x² + x − 1

17. f(x) = x³ + 5x − 4

18. f(x) = 2x³ + x²

19.

20.

21.

22.

23.

24.

25.

26.

In Problems 27–32, use the appropriate derivatives obtained in Problems 11–26. For the given function, find the point of tangency and slope of the tangent line at the indicated value of x. Find an equation of the tangent line at that point.

27. f(x) = 3x² − x + 7, x = 2

28. f(x) = x² − x, x = 3

29. f(x) = x³ + 5x − 4, x = 1

30.

31.

32.

In Problems 33–40, proceed as in Example 6.

(a) Compute the difference quotient for the given function.

(b) Then, if instructed, compute the derivative

33. f(x) = 3x² + 1

34. f(x) = x² − 8x − 3

35. f(x) = 10x³

36. f(x) = x⁴

37.

38.

39.

40.

For Discussion

41. Use either (3) or (4) to compute the derivative of f(x) = x³ – 3x² – 9x. Find the points on the graph of f at which f'(x) = 0. Interpret your answers geometrically.

42. Use either (3) or (4) to compute the derivative of f(x) = x^1/3. [Hint: Recall from Section 1.5, a³ − b³ = (a − b)(a² + ab + b²).]

43. What is the tangent line to the graph of a linear function f(x) = ax + b?

44. If f ' (x) > 0 for every x in an interval, then what can be said about f on the interval? If ' (x) < 0 for every x in an interval, then what can be said about f on the interval? [Hint: Draw a graph.]

45. If f is an even function and if (x, y) is on the graph of f, then (−x, y) is also on the graph of f. How are the slopes of the tangent lines at (x, y) and (−x, y) related?

46. If f is an odd function and if (x, y) is on the graph of f, then (−x, −y) is also on the graph of f. How are the slopes of the tangent lines at (x, y) and (−x, −y) related?

47. Consider the semicircle whose equation is . Discuss: How can the derivative f ' (x) be found using only the geometric fact that the radius of a circle is perpendicular to the tangent line at a point (x, y) on the circle?

48. Consider the semicircle whose equation is . Use (3) to find the derivative f ' (x) and compare your result with that in Problem 47.

49. Find an equation of the tangent line, shown in red in FIGURE 2.9.8, to the graph of y = f(x) at point P. What are f(−3) and f '(−3)?

FIGURE 2.9.8 Graph for Problem 49

50. Find an equation of the tangent line, shown in red in FIGURE 2.9.9, to the graph of y = f(x) at point P. What is f '(3)? What is the y-intercept of the tangent line?

FIGURE 2.9.9 Graph for Problem 50

 

CHAPTER 2 Review Exercises
Answers to selected odd-numbered problems begin on page ANS–8.

In Problems 1–20, fill in the blanks.

1. If is a point on the graph of f.

2. If and f(2) = 3, then A = ______.

3. The domain of the function is______.

4. The range of the function f(x) = |x| − 10 is______.

5. The zeros of the function are______.

6. If the graph of f is symmetric with respect to the y-axis, f(−x) = ______.

7. The lines 2x − 5y = 1 and kx + 3y + 3 = 0 are parallel if k =______.

8. The x- and y-intercepts of the line −4x + 3y − 48 = 0 are______.

9. The graph of a linear function for which f(−2) = 0 and f(0) = − 3 has slope m =______.

10. An equation of a line through (1, 2) that is perpendicular to y = 3x − 5 is______.

11. The x- and y-intercepts of the parabola f(x) = x² − 2x − 1 are______.

12. The range of the function f(x) = − x² = 6x − 21 is______.

13. The quadratic function f(x) = ax² = bx = c for which f(0) = 7 and whose only x-intercept is (−2, 0) is f(x) =______.

14. If f(x) = x + 2 and g(x) = x² − 2x, then (f ° g) (−1) =______.

15. The vertex of the graph of f(x) = x² is (0, 0). Therefore, the vertex of the graph of y = − 5(x − 10)² = 2 is______.

16. Given that is the inverse of a one-to-one function f, and without finding f, the domain of f is______and range of f is______.

17. The x-intercept of a one-to-one function f is (5, 0), and so the y-intercept of f⁻¹ is______.

18. The inverse of is f −¹ =______.

19. The point (a, 16a) lies on the graph of

for a =______.

20. For f(x) = [x = 2] − 4, f(− 5.3) =______.

In Problems 21–40, answer true or false.

21. The points (0, 3), (2, 2), and (6, 0) are collinear.______

22. The graph of a function can have only one y-intercept.______

23. If f is a function such that f(a) = f(b),then a = b.______

24. No nonzero function f can be symmetric with respect to the x-axis.______

25. The domain of f (x) = (x − 1)^1/3is (− ∞, ∞).______

26. If f(x) = x and , then the domain of g/f is [−2, ∞).______.

27. A function f is one-to-one if it never takes on the same value twice.______

28. Two lines with positive slopes cannot be perpendicular.______

29. The equation of a vertical line through (2, − 5) is x = 2.______

30. A point of intersection of the graphs of f and f^-1 must lie on the line y = x.______

31. The one-to-one function f(x) = 1/x has the property that f = f^-1.______

32. The function f(x) = 2x² + 16x − 2 decreases on the interval [−7, −5].______

33. No even function can be one-to-one.______

34. All odd functions are one-to-one.______

35. If a function f is one-to-one, then .______

36. If f is an increasing function on an interval containing x₁ < x₂, then f(x₁)< f(x₂)._____

37. The function f(x) = |x| − 1 is decreasing on the interval [0, ∞).______

38. For function composition, f ° (g + h) = f °g + f°h.______

39. If the y-intercept for the graph of a function f is (0, 1), then the y-intercept for the graph of y = 4 − 3f(x) is (0, 1).______

40. For any function f, f(x₁ + x₂) = f(x₁) + f(x₂).______

In Problems 41 and 42, identify two functions f and g so that h = f ° g.

41.

42.

43. Write the equation of each new function if the graph of f(x) = x³ − 2 is

(a) shifted to the left 3 units.

(b) shifted down 5 units.

(c) shifted to the right 1 unit and up 2 units.

(d) reflected in the x-axis.

(e) reflected in the y-axis.

(f) vertically stretched by a factor of 3.

44. FIGURE 2.R.1 shows the graph of a function f whose domain is (−∞, ∞). Sketch the graph of the following functions.

(a) y = f(x) − π

(b) y = f(x − 2)

(c)

(d) y = −f(x)

(e) y = f(− x)

(f) y = 2f(x)

FIGURE 2.R.1 Graph for Problem 44

In Problems 45 and 46, use the graph of the one-to-one function f in Figure 2.R.1.

45. Give the domain and range of f^-1.

46. Sketch the graph of f^-1.

47. Express y = x − |x| + |x − 1|as a piecewise-defined function. Sketch the graph of the function.

48. Sketch the graph of the function y = [x] = [−x]. Give the numbers at which the function is discontinuous.

In Problems 49 and 50, by examining the graph of the function f give the domain of the function g.

49.

50.

In Problems 51 and 52, the given function f is one-to-one. Find f^-1.

51. f(x) = (x + 1)³

52.

53. Express the area of the shaded region in FIGURE 2.R.2 as a function of h.

FIGURE 2.R.2 Circle in Problem 53

54. Determine a quadratic function that describes the parabolic arch shown in FIGURE 2.R.3.

FIGURE 2.R.3 Arch in Problem 54

55. The diameter d of a cube is the distance between opposite vertices as shown in FIGURE 2.R.4. Express the diameter d as a function of the length s of a side of the cube by first expressing the length y of the diagonal in Figure 2.R.4 as a function of s.

FIGURE 2.R.4 Cube in Problem 55

56. A circular cylinder of height h is inscribed in a sphere of radius 1 as shown in FIGURE 2.R.5. Express the volume of the cylinder as a function of h.

FIGURE 2.R.5 Inscribed cylinder in Problem 56

57. A baseball diamond is a square that is 90 ft on a side. See FIGURE 2.R.6. After a player hits a home run, he jogs around the bases at a rate of 6 ft/s.

(a) As the player jogs between home base and first base, express his distance from home base as a function of time t, where t = 0 corresponds to the time he left home base—that is, 0 ≤ t ≤ 15.

(b) As the player jogs between home base and first base, express his distance from second base as a function of time t, where 0 ≤ t ≤ 15.

FIGURE 2.R.6 Baseball player in Problem 57

FIGURE 2.R.7 Circles in Problem 58

58. Consider the four circles shown in FIGURE 2.R.7. Express the area of the shaded region between them as a function of h.

In Problems 59–62, find the objective function for the given calculus problem. Do not actually attempt to solve the problem.

59. Find the minimum value of the sum of 20 times a positive number and 5 times the reciprocal of that number.

60. A rancher wants to use 100 m of fence to construct a diagonal fence connecting two existing walls that meet at a right angle. How should this be done so that the area enclosed by the walls and fence is a maximum?

61. The running track shown as the black outline curve in FIGURE 2.R.8 is to consist of two parallel straight parts and two semicircular parts. The length of the track is to be 2 km. Find the design of the track so that the rectangular plot of land enclosed by the track is a maximum.

FIGURE 2.R.8 Running track in Problem 61

62. A pipeline is to be constructed from a refinery across a swamp to storage tanks. See FIGURE 2.R.9. The cost of construction is $25,000 per mile over the swamp and $20,000 per mile over land. How should the pipeline be made so that the cost of construction is a minimum?

In Problems 63–66, compute for the given function. Find an equation of the tangent line at the indicated value of x.

63. f(x) = − 3x² + 16x + 12, x = 2

64. f(x) = x³ − x², x = − 1

65.

66.

FIGURE 2.R.9 Pipeline in Problem 62

---

* Many instructors like to call x the input of the function and f(x) the output.

* We leave the discussion of the many subtleties and questions surrounding the tangent line problem to a course in calculus.