5

Number Theory

1. What are prime numbers and relatively prime numbers?

Ans.: Any positive integer greater than 1 is a prime number if and only if it is divisible by only two integers, 1 and itself. For example, the numbers 2, 3, 5, 7, 11, 13, 17 and 19 are all prime numbers, whereas the numbers 4, 6, 8 and 10 are composite (means not prime), because they have more than two divisors.

Two positive integers a and b are said to be relatively prime, or co-prime, if gcd(a, b)= 1. In other words, two numbers are said to be relatively prime if they have no common factors except the integer 1. For example, the integers 14 and 15 are relatively prime; however, the integers 14 and 16 are not relatively prime because they have a common factor other than the integer 1. Note that the integer 1 is relatively prime with any integer. Also, if n is a prime number, all integers ranging from 1 to n-1 are relatively prime to n.

2. State and prove Fermat's theorem.

Ans.: Fermat's theorem, also called Fermat's little theorem, plays an important role in public-key cryptography. The theorem states that if p is a prime number and x is a positive integer not divisible by p, then:

xp-1 ≡ 1 (mod p)

In other words, we can say that:

xp-1 mod p = 1

Proof

Consider a set of integers Zp={1, 2,…, p-1} where each element of Zp is relatively prime to p.

If all elements of Zp are multiplied by x, and the result is mapped to Zp using modular arithmetic, we get another set (say, S), as shown here:

S = {x mod p, 2x mod p,…, (p-1)x mod p}

As x is not divisible by p, none of the elements of S is zero. Also, no two elements of S are equal. Thus, we can say that the set S contains the elements of Zp, that is, {1, 2,…, p-1} in some order. On multiplying the elements in both the sets and taking the result modulo p, we get:

As p and (p-1) are relatively prime, the term (p-1)! can be cancelled out from both sides. Thus, equation (1) becomes:

xp-1 ≡ 1 (mod p)

Hence, proved.

There is another version of Fermat's theorem which states that, if p is a prime number and x is a positive integer, then:

xp ≡ x (mod p)

3. Explain Euler's totient function.

Ans.: Euler's totient function, also called Euler's phi function [denoted as Φ(n)], has an important role in cryptography. The value of this function is the number of positive integers that are smaller than n and relatively prime to n. The set of these numbers is represented by Zn.

A set of rules is to be followed while calculating the value of Φ(n) in the set Zn. These rules are as follows:

Rule 1: Φ(1)= 1

Rule 2: Φ(p)= p-1, if p is a prime number

Rule 3: Φ(m * n)= Φ(m)* Φ(n), if m and n are relatively prime

Rule 4: Φ(pe)= pe-pe-1, if p is prime

To compute Φ(n), suppose that we have two prime numbers p and q, such that p ≠ q and n = pq. Thus, we can write:

For example, for n = 21

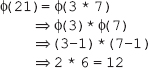
From the preceding example, it is clear that there are 12 integers that are smaller than the number 21 and relatively prime to 21.

4. State and prove Euler's theorem with the help of an example.

Ans.: Euler's theorem is also known as Fermat-Euler theorem or Euler's totient theorem. This theorem has two forms. The first form of Euler's theorem states that for every positive integer x that is relatively prime to n,

xΦ(n) ≡ 1(mod n)

Proof

If n is a prime number, then Φ(n)= n-1. Thus, the preceding equation becomes xn-1 ≡ 1(mod n), which is true by the Fermat's theorem, discussed in Question 2. Now, consider the case when n is not prime.

Let us consider a set R = {a1, a2, …, aΦ(n)}, where each ai is less than n and relatively prime to n. Multiplying each element of the set R by x and taking the result mod n, we get another set S, as shown here:

S = {(xa1 mod n),(xa2 mod n),…,(xaΦ(n) mod n)}

The set S is a permutation of R, because of the following reasons:

   As ai and x are relatively prime to n, xai must also be relatively prime to n. Thus, all the elements of S are positive integers that are less than n and relatively prime to n.

   The set S does not contain any duplicate elements. That is, if xai mod n = xaj mod n, then ai = aj.

Therefore, we can write that:

Hence, proved.

The alternative form of Euler's theorem states that:

xΦ(n)+1 ≡ x mod n

Unlike the first form, this form does not require x be relatively prime to n.

5. What is primality testing? What are its categories?

Ans.: In cryptographic algorithms, we often need to create large prime numbers. The selection of such numbers is a very challenging task. Thus, an algorithm is needed that can efficiently check whether a given large number is prime or composite. That is, we need an algorithm that can efficiently perform primality test on numbers. The algorithms for checking the primality are divided into two categories: deterministic and probabilistic.

   Deterministic algorithms: As the name suggests, these algorithms determine whether a given number is prime or not. They accept a number (say, p) as input and output the result, either that p is prime or that p is composite. There are two types of deterministic algorithms, which are as follows:

   Basic algorithm: A simple way to check whether a number p is prime or not is to divide p by all values m (from 2 to p-1) and check whether p is fully divisible by any value of m. If so, then p is composite; else, it is prime.

   Divisibility algorithm: In this algorithm, instead of testing up to p-1, testing up to only √p is sufficient. The reason behind this is that if p is composite, then it can be factored into two values, and at least one of the values must be less than or equal to √p. Thus, if the number p is divisible by any of the prime numbers less than √p, then it is composite.

   Probabilistic algorithms: As the name suggests, these tests are based on the probability theory and are used to check the probability of a number being prime. These algorithms are also referred to as randomized algorithms. They accept an integer p and output the probability of p being prime. There are two types of tests based on the probability theory.

   Fermat's primality test: This is a probabilistic test that checks whether a number is prime or not. We check the probability of the Fermat's little theorem to be true or false. As we know that the theorem states that if p is prime and x is relatively prime to p such that 1 < x < p ε Zp, then:

xp-1 ≡ 1 (mod p)

     To test whether p is prime or not, we pick a random number x from Zp and check whether equality holds. If equality does not hold, then p is composite, whereas if equality holds for many values of x, then p is said to be probably prime or pseudoprime. Usually, it is not possible to check the equality for all values of x. In case we pick such a value of x for which the equality holds, but p is composite, then x is known as a Fermat liar. In contrast, if we do pick a value for x such that the equality fails and p is also composite, then x is known as Fermat witness for the compositeness of p.

   Miller-Rabin test: It is also a probabilistic test to check whether a number taken at random is prime or not. This test returns the result as composite if p is not prime, or as inconclusive if p may or may not be a prime number. We check the probability of the number being composite or inconclusive with the help of an algorithm given by Miller and Rabin.

6. Give the Miller-Rabin algorithm for testing primality.

Ans.: The Miller-Rabin algorithm (also known as the Rabin-Miller test) is used to test a large number for primality. It is a polynomial-time algorithm with a run-time complexity of O((log n)3).

As we know, a positive odd integer p can be written in the power of 2 as follows:

p-1 = 2kq

Where, q is an odd number that is obtained by dividing (p-1) by 2, and k is the number of times and k > 0.

For example, let p = 37. Then, p-1 = 36, which can be written as 36 = 2² * 9. Here, 9 is obtained when 36 is divided twice by 2.

In Miller-Rabin algorithm, we take into account two basic properties of prime numbers, which are as follows.

1.   If p is a prime number and x is a positive integer (1 < x < p), then x2 mod p = 1 if and only if x mod p = 1 or x mod p = -1. As in modular arithmetic, -1 mod p =(p-1); therefore, x mod p = -1 means x mod p =(p-1). As we know, (x mod p)*(x mod p)= x2 mod p. Hence, whether x mod p = 1 or x mod p = -1, we always get x2 mod p = 1.

2.   If p is a prime number greater than 2, we can say that p-1 = 2kq where k > 0 and q is odd, then any one of the following conditions is true:

   xq mod p = 1 or xq ≡ 1 (mod p)

   One of the numbers from(xq, x2q, x4q,…, x2(k-1)q, x2kq) is congruent to -1 modulo p. This implies that there is some j in the range(1 ≤ j ≤ k)such that:

x2(j-1)q mod p = -1 or x2(j-1)q mod p = p-1.

After considering these two properties, we can come to the conclusion that a number p can be prime if either the first element of the list (xq, x2q,x4q,…, x2(k-1)q, x2kq) modulo p is equal to 1 or if some element in this list (say, x2(j-1)q) modulo p is equal to p-1. If neither of the conditions is satisfied, the number p is not prime (that is, it is composite).

Here, it is important to note that if the condition is satisfied, it does not necessarily mean that p is prime. That is, even if the condition is satisfied, p may or may not be prime. For example, let p = 2047. Then p-1, that is, 2046, can be written as 2 * 1023, yielding k = 1 and q = 1023. Now, as 21023 mod 2047 = 1, 2047 should be prime; however, it is not. Thus, it is clear that even though a number may satisfy a condition, it may not be prime.

Miller-Rabin algorithm

Let p be an integer to be checked for primality. The algorithm returns the result as composite if p is not prime and inconclusive if p may or may not be a prime number.

1.   Find integers k and q where k > 0 and q is odd such that (p-1 = 2kq).

2.   Choose a random integer x such that 1< x < p-1

3.   S:= xq mod p

4.   If S = 1, then print (‘inconclusive’)and exit

5. for j = 0 to k-1
{
 S:= x2jq mod p          //equivalent to S:= S2 mod p
 if S = p-1
      print(‘inconclusive’)and exit
}

6.   print(‘composite’)

7. Describe and illustrate the Chinese Remainder Theorem.

Ans.: Chinese Remainder Theorem (CRT) is so named as it was discovered by the Chinese mathematician Sun-Tsu in around 100 AD. It is used to solve a set of congruent equations with a single variable but different moduli, which are relatively prime. Consider such a set of equations as shown here:

a = x1 mod m1
a = x2 mod m2
.
.
.
a = xk mod mk

All these equations have a unique solution if the moduli for the equations are pair-wise relatively prime, that is, gcd(mi, mj) = 1. In case the moduli are not relatively prime but satisfy other conditions, then even we can have the solution. In cryptography, we prefer to solve the equations with relatively prime moduli.

The solution to the set of simultaneous equations can be obtained by performing the following steps:

1.   Find the common modulus, M = m1* m2*…* mk.

2.   Find M1 = M/m1, M2 = M/m2,…, Mk = M/mk.

3.   Find the multiplicative inverse of M1, M2,…, Mk using the corresponding moduli m1, m2,…, mk. Let the inverses be M1-1, M2-1,…, Mk-1.

4.   The solution to the simultaneous equations is:

a =(x1 * M1 * M1-1 + x2 * M2 * M2-1 +…+ xk * Mk * Mk-1) mod M

8. Define the following terms:

(a) Finite multiplicative group

(b) Order of the group

(c) Order of an element

(d) Primitive roots of a group

(e) Cyclic group

Ans.: (a) Finite multiplicative group: A finite multiplicative group is often used in cryptography. It is represented as G = <, *>
     Where:
        G = finite multiplicative group
         = a set containing integers between 1 and n-1 that are relatively prime to n
        * = the multiplication operation
     The identity element (e) of the finite multiplicative group G is equal to 1.

(b) Order of the group: As we know, the order of a group is the number of elements in the group. For a finite multiplicative group G = <, *>, the order of the group is Φ(n), where Φ(n) is the Euler's totient function.

(c) Order of an element: For a finite multiplicative group G = <, *>, the order of an element (say, a), represented as Ord(a), is the smallest integer i such that ai ≡ e(mod n), where e is the identity element of the group G. Here, the value of e is 1.

(d) Primitive roots of a group: For a finite multiplicative group G = <,*>, the primitive roots are the elements that have the order equal to Φ(n). The number of primitive roots in a group is equal to Φ(Φ(n)).

(e) Cyclic group: If a finite multiplicative group G = <, *> has primitive roots, it is called a cyclic group. Each primitive root of the cyclic group can be used to generate the elements of the set , thus termed as generator. If x is a generator, then elements can be created using xa modulo n, where a is an integer ranging from 1 to Φ(n), as shown here:

={x1 mod n, x2 mod n, x3 mod n,…, xΦ(n) mod n}

      Notice that a finite multiplicative group G = <, *> is always cyclic if p is a prime number.

9. Write a short note on discrete logarithmic problems.

Ans.: In cryptography, exponentiation and modular logarithm are often used. Exponentiation and logarithm are reverse of each other. Whenever exponentiation is used to encrypt the plaintext or decrypt the ciphertext, the opponent can use logarithm to attack. Thus, it is required to identify how difficult it is to reverse the exponentiation. An approach to determine this is to use the concept of discrete logarithm.

Consider a finite multiplicative group G = <, *>, where p is prime. The elements of this group are the integers from 1 to p-1. In addition, the group is cyclic, as p is prime and thus has primitive roots. The primitive roots of such a group can be considered as the base of the logarithm. Thus, in case the group has m primitive roots, the calculation can be performed in m different bases.

Let us consider a as a primitive root of group G. Then, an element (say, y) of can be created as:

y = ax mod p

Where, x is an integer ranging from 1 to Φ(p) (which is p-1, in this case). Suppose we are given the value of y, and we are to find the value of x. Such type of problem is referred to as a discrete logarithmic problem, and the solution to this problem is given as:

x = logay mod p

That is, we need to find the log of y in base a, and then take the result mod p.

10. Find out the result of 3¹² mod 11.

Ans.: We can write:

Now, according to second version of Fermat's theorem, xp ≡ x(mod p)or xp mod p = x. Thus, we get (311 mod 11)= 3. Also, (3 mod 11)= 3. Putting both these values in equation (1), we have:

11. Find out the result of 5¹² mod 13.

Ans.: We can write:

512 mod 13 = 513-1 mod 13

Now, according to Fermat's theorem for a prime number p, which states that xp-1 mod p = 1, we have:

513-1 mod 13 = 1, as 13 is a prime number.

12. Find Φ(7).

Ans.: As 7 is a prime number, according to Rule 2 of the Euler's totient function [f(n)= n-1], we have:

This implies that there are six positive integers that are less than 7 and relatively prime to 7. These integers include 1, 2, 3, 4, 5 and 6.

13. Find Φ(10).

Ans.: The integer 10 is a multiple of 5 and 2, therefore, we can write:

Φ(10)= Φ(5*2)

As 5 and 2 are relatively prime, by applying Rule 3 of Euler's totient function [Φ(m * n)= Φ(m)* Φ(n)], we can write:

14. Check whether 89 is a prime.

Ans.: To check 89 for primeness, we can apply the divisibility test, where we check whether 89 is divisible by any of the prime numbers less than √89. Now, the integral value of √89 is 9 and the prime numbers less than 9 are {2, 3, 5, 7}. As 89 is not divisible by any of these numbers, it is a prime.

15. Apply Miller-Rabin's algorithm and use base 2 to test whether the number 561 passes the test.

Ans.: Using Miller-Rabin algorithm, explained in Question 6, we can test the number 561 as follows:

As for no value of j, S is equal to 560. Thus, 561 is composite.

16. Solve the following simultaneous congruence using Chinese Remainder Theorem to find the value of a.

a ≡ 2 mod 3

a ≡ 3 mod 5

a ≡ 2 mod 7

Ans.: Applying Chinese Remainder Theorem, explained in Question 7, the solution to the given equations is obtained as follows:

Step 1: Given m1 = 3, m2 = 5, m3 = 7
                 Thus, the common modulus, M = 3*5*7 = 105

Step 2: Compute M₁, M₂ and M₃.
                 

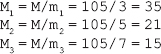
Step 3: Compute the multiplicative inverse of M1, M2 and M3 in modulo m1, m2 and m3, respectively.
                 

Step 4: The solution to the simultaneous equations is as follows:
                 

Thus, the value of a is 23.

17. Find the order of all the elements in G = <,*>. Also find the primitive roots in the group G.

Ans.: For the group G = <, *>, the set contains those integers between 1 and 6 that are relatively prime to 7. That is, = {1, 2, 3, 4, 5, 6}. The order of this group = Φ(7)= 6.

For each element a of the set , we will find out for which value of i (from 1 to 6), the condition ai ≡ 1(mod n), that is, ai mod n = 1, holds true. That value of i will be the order of the element.

1.   For a = 1,
11 mod 7 = 1
Thus, the order of element 1, that is, Ord(1)= 1.

2.   For a = 2,
21 mod 7 = 2 ≠ 1
22 mod 7 = 4 mod 7 = 4 ≠ 1
23 mod 7 = 8 mod 7 = 1
Thus, the order of element 2, that is, Ord(2)= 3.

3.   For a = 3,
3¹ mod 7 = 3 ≠ 1
3² mod 7 = 9 mod 7 = 2 ≠ 1
3³ mod 7 = 27 mod 7 = 6 ≠ 1
3⁴ mod 7 = 81 mod 7 = 4 ≠ 1
3⁵ mod 7 = 243 mod 7 = 5 ≠ 1
3⁶ mod 7 = 729 mod 7 = 1
Thus, the order of element 3, that is, Ord(3)= 6.

4.   For a = 4,
41 mod 7 = 4 mod 7 = 4 ≠ 1
42 mod 7 = 16 mod 7 = 2 ≠ 1
43 mod 7 = 64 mod 7 = 1
Thus, the order of element 4, that is, Ord(4)= 3.

5.   For a = 5
51 mod 7 = 5 ≠ 1
52 mod 7 = 25 mod 7 = 4 ≠ 1
53 mod 7 = 125 mod 7 = 6 ≠ 1
54 mod 7 = 625 mod 7 = 2 ≠ 1
55 mod 7 = 3125 mod 7 = 3 ≠ 1
56 mod 7 = 15625 mod 7 = 1
Thus, the order of element 5, that is, Ord(5)= 6.

6.   For a = 6,
61 mod 7 = 6 ≠ 1
62 mod 7 = 36 mod 7 = 1
Thus, the order of element 6, that is, Ord(6)= 2.

Only the elements 3 and 5 have the order equal to Φ(7), that is, 6, and therefore the primitive roots of the group G are 3 and 5.

18. Find the value of x in the group G =(,*)for the following cases with the help of the given table.

(a) 4 ≡ 3x mod 7

(b) 6 ≡ 5x mod 7

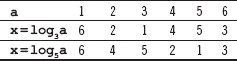
Ans.: For the group G =(,*), Φ(7)= 6 and ={1, 2, 3, 4, 5, 6}. The given equations are of the form a = bx mod n. These equations can be solved using the table for each and different bases, as provided in the question.

(a) 4 ≡ 3x mod 7
Here, a = 4. Thus, x = log34 mod 7

From the given table, it is clear that log34 = 4. Therefore,
x = 4 mod 7
4

(b) 6 ≡ 5x mod 7
Here, a = 5. Thus, x = log56 mod 7

From the given table, it is clear that log56 = 3. Therefore,
x = 3 mod 7
3

Multiple-choice Questions

1.   What is the value of Φ(1)?

(a) Zero

(b) One

(c) Not defined

(d) None of these

2.   The gcd of 14 and 15 is __________.

(a) One

(b) Two

(c) Three

(d) Four

3.   Two positive integers a and b are said to be relatively prime if __________.

(a) Their gcd is 1

(b) They have no common prime factors

(c) If 1 is their only common divisor

(d) All of these

4.   Which of the following is used for testing primality?

(a) Fermat's primality test

(b) Miller-Rabin

(c) Divisibility test

(d) All of these

5.   Chinese remainder theorem is given by __________

(a) Fermat

(b) Euler

(c) Sun-Tsu

(d) Miller and Rabin

6.   The number of primitive roots in a group is computed by __________

(a) Φ(Φ(n))

(b) Φ(n)

(c) Ord(n)

(d) None of these

Answers

1. (b)

2. (a)

3. (d)

4. (d)

5. (c)

6. (a)