2

Cryptography and Finite Fields

1. Explain the term cryptography in brief.

Ans.: Cryptography is a means for implementing some security mechanisms. The term cryptography is derived from the Greek word kryptos, which means “secret writing”. In simple terms, cryptography is the process of altering messages in a way that their meaning is hidden from adversaries who might intercept them. It allows the sender to disguise a message to prevent it from being read or altered by an intruder, and it also enables the receiver to recover the original message from the disguised one.

In data and telecommunications, cryptography is an essential technique required for communicating over any untrusted medium, which includes any network, such as the Internet. By using cryptographic techniques, the sender can first encrypt a message and then transmit it through the network. The receiver on the other hand can decrypt the message and recover its original contents.

Cryptography relies upon two basic components: an algorithm (or cryptographic methodology) and a key. Algorithms are the complex mathematical formulae and keys are the strings of bits. For two parties to communicate over a network (the Internet), they must use the same algorithm (or algorithms that are designed to work together). In some cases, they must also use the same key.

2. Define the following terms:

(a) Plaintext

(b) Ciphertext

(c) Encryption

(d) Decryption

(e) Cipher

(f) Key

Ans.: These terms can be defined as follows:

(a) Plaintext: It refers to the original unencrypted message that the sender wishes to send.

(b) Ciphertext: It refers to the encrypted message that is received by the receiver.

(c) Encryption: It is the process of encrypting the plaintext so that the ciphertext can be produced. Plaintext is transformed into ciphertext using the encryption algorithm.

(d) Decryption: It is the reverse of the encryption process. In this process, the ciphertext is converted back to the plaintext using a decryption algorithm.

(e) Ciphers: The encryption and decryption algorithms are together known as ciphers. Ciphers need not necessarily be unique for each communicating pair; rather a single cipher can be used for communication between multiple pairs of senders and receivers.

(f) Key: A key is usually a number or a set of numbers on which the cipher operates. Encryption and decryption algorithms make use of a key to encrypt or decrypt messages, respectively. At the sender's end, the encryption algorithm and encryption key are required to convert the plaintext into ciphertext. At the receiver's end, a decryption algorithm uses the decryption key to convert ciphertext back into the plaintext. The longer the key is, the harder it is for an attacker to decrypt the message.

3. Explain symmetric-key and asymmetric-key encipherment.

Ans.: Traditionally, cryptography involves the use of the same key for encrypting or decrypting the messages (symmetric-key encipherment). However, modern cryptography involves the use of different keys for encryption and decryption (asymmetric-key encipherment).

Symmetric-key Encipherment

The symmetric-key encipherment, sometimes also called secret-key encipherment or secret-key cryptography, uses a single shared key (secret key) for both encryption and decryption of data. Thus, it is obvious that the key must be known to both the sender and the receiver. As shown in Figure 2.1, the sender uses the shared key and the encryption algorithm to transform the plaintext into ciphertext. The ciphertext is then sent to the receiver via a communication network. The receiver applies the same key and the decryption algorithm to decrypt the ciphertext and to recover the plaintext. Some examples of symmetric-key algorithms include Data Encryption Standard (DES), double DES, triple DES, and Advanced Encryption Standard (AES).

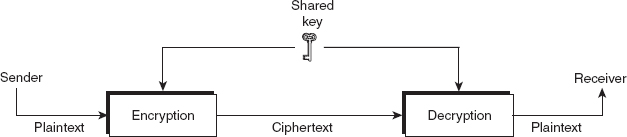
Figure 2.1 Message exchange using secret key

The main problem in secret-key cryptography is getting the sender and receiver to agree on the secret key without anyone else finding it out. If the key is compromised, the security offered by secret-key cryptography is severely reduced or eliminated. Secret-key cryptography assumes that the parties who share a key rely upon each other not to disclose the key and protect it against modification. If they are in separate physical locations, they must trust a medium such as the courier or a phone system to prevent the disclosure of the secret key. Anyone who overhears or intercepts the key in transit can later read, modify, and forge all messages encrypted or authenticated using that key.

Asymmetric-key Encipherment

The asymmetric-key encipherment, sometimes also called public-key encipherment or public-key cryptography, was introduced by Diffie and Hellman in 1976 to overcome the problem found in symmetric-key cryptography. It involves the use of two different keys for encryption and decryption. These two keys are referred to as the public key (used for encryption) and the private key (used for decryption). Each authorized user has a pair of public and private keys. The public key of each user is known to everyone, whereas the private key is known to its owner only.

Now, suppose that a user A wants to transfer some information to user B securely. The user A encrypts the data by using the public key of B and sends the encrypted message to B. On receiving the encrypted message, B decrypts it by using his/her private key. Since decryption process requires a private key of user B, which is only known to B, the information is transferred securely. Figure 2.2 illustrates the whole process. RSA is a well-known example of asymmetric-key algorithm.

Figure 2.2 Message exchange using public key

The main advantage of public-key cryptography is that the need for the sender and the receiver to share the secret key is eliminated and all communication involves only public keys. Thus, the private key is never transmitted or shared. Anyone can send a confidential message using a public key, but the message can only be decrypted with a private key, which is in the sole possession of the intended recipient.

4. Differentiate between symmetric-key and asymmetric-key cryptography.

Ans.: Some differences between symmetric-key and asymmetric-key cryptography are listed in Table 2.1.

Table 2.1 Differences Between Symmetric-key and Asymmetric-key Cryptography

Symmetric-key cryptography	Asymmetric-key cryptography
1. It uses a single key for both encryption and decryption of data.	1. It uses two different keys—public key for encryption and private key for decryption.
2. Both the communicating parties share the same algorithm and the key.	2. Both the communicating parties should have at least one of the matched pair of keys.
3. The processes of encryption and decryption are very fast.	3. The encryption and decryption processes are slower as compared to symmetric-key cryptography.
4. Key distribution is a big problem.	4. Key distribution is not a problem.
5. The size of encrypted text is usually same or less than the original text.	5. The size of encrypted text is usually more than the size of the original text.
6. It can only be used for confidentiality, that is, only for encryption and decryption of data.	6. It can be used for confidentiality of data as well as for integrity and non-repudiation checks (that is, for digital signatures).
7. DES and AES are the commonly used symmetric-key algorithms.	7. The most commonly used asymmetric-key algorithm is RSA.

5. What is cryptanalysis? Also, discuss different cryptanalysis attacks.

Ans.: Cryptanalysis is the art and science of breaking the encrypted codes that are created by applying some cryptographic algorithms. The person who performs cryptanalysis is known as a cryptanalyst. A cryptanalysis attack is made by a cryptanalyst to obtain the plaintext or the key that was used to encrypt a message. Depending on the information that the cryptanalyst has, cryptanalysis attacks can be classified under the following categories:

   Ciphertext-only attack: In this type of attack, the cryptanalyst has a part of the ciphertext available and using this information, he/she tries to find out the corresponding key and decipher the plaintext. This attack is based on the assumption that the cryptanalyst knows the algorithm that has been used to encrypt the message and can easily intercept the ciphertext. These types of attacks are very common because the attacker just needs to have the knowledge of the ciphertext. However, we can prevent a cryptanalyst from decrypting the ciphertext by using a strong cipher, which makes it very difficult for the cryptanalyst to decrypt the message. Some common methods that can be used to determine the key or break the ciphers in ciphertext-only attacks include brute-force, statistical, and pattern attacks. Figure 2.3 depicts the process of ciphertext-only attack where A and B are the communicating parties and C is the cryptanalyst (attacker).

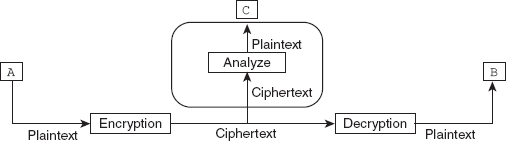
Figure 2.3 Ciphertext-only attack

   Known-plaintext attack: In this type of attack, the attacker already has some plaintext-ciphertext pairs in addition to the ciphertext that he/she wishes to break. Figure 2.4 depicts the process of known-plaintext attack by C during communication between A and B. Suppose that A sent a secret message to B; however, later, A made the contents of that message public. Further, assume that the attacker C has kept both ciphertext and plaintext (which is now public). Thus, C tries to obtain a relationship between these pairs to find the key used to encrypt the plaintext so that he/she can break the next block of ciphertext from A to B; provided that A uses the same key to encrypt the message as that for the previous message. This type of attack is easy to implement because the attacker has more information to analyze the ciphertext. However, this attack happens rarely because it is more likely that the sender changes the key for every transmission of message, or that the message contents are not made public.

Figure 2.4 Known-plaintext attack

   Chosen-plaintext attack: This attack is similar to the known-plaintext attack with the only difference being that in this attack, the attacker C himself/herself chooses the plaintext–ciphertext pairs. However, it is possible only if C gets access to A's computer by some means. The attacker C can then select some plaintext from A's computer that helps him/her to intercept the created ciphertext. This process is shown in Figure 2.5.

Figure 2.5 Chosen-plaintext attack

   Chosen-ciphertext attack: A chosen-ciphertext attack is similar to a chosen-plaintext attack. The only difference between the two being that in chosen-ciphertext attack, the attacker C chooses some ciphertext and then decrypts it to make a ciphertext-plaintext pair. This is possible if C gets access to B's computer. This process is shown in Figure 2.6.

Figure 2.6 Chosen-ciphertext attack

   Chosen-text attack: A chosen-text attack is a combination of chosen-plaintext and chosen-ciphertext attack.

6. What is key management? Also, explain the functions of key management.

Ans.: Though cryptography enables maintaining the secrecy of a message, it works only as long as the keys used for encryption and decryption are kept secret. Thus, the secrecy of cryptographic keys is central to the encryption mechanism, and it is achieved through key management. Key management refers to the collection of processes used for the generation, storage, installation, transcription, recording, change, disposition, and control of keys that are used in cryptography. It is essential to the secure ongoing operation of any cryptosystem. The various functions of key management are as follows:

   Generation: This process involves the selection of a key that is to be used for encrypting and decrypting the messages. The key may be generated for the sender, receiver, or an application. It must be long enough to be predicted by a cryptanalyst. Moreover, it must be chosen randomly and its information must not be leaked during the whole process.

   Distribution: This process involves all the efforts made in carrying the key from the point where it is generated to the point where it is to be used. Distribution is more difficult in symmetric-key cryptography where the key has to be transmitted via a secure channel.

   Installation: This process involves getting the key into the storage of the device or the process that needs to use this key. Note that if this process involves manual operations, then it might result in leakage of key information.

   Storage: This process involves maintaining the confidentiality of stored or installed keys while preserving the integrity of the storage mechanism. The mechanism may be designed in such a way that once the key is installed, no one from the outside the encryption machine can intercept it. Alternatively, for an effective implementation, the key may be stored in an encrypted form such that the knowledge of the stored key does not disclose the behaviour of the device in which the key is being used.

   Change: This process involves ending with the use of one key and starting the use of another. The longer the key is in use and more is the traffic encrypted by it, higher are the chances that it will be intercepted. Therefore, the key must be changed after some time. It may noted that the information about the key is prone to leakage during the key change time.

7. Describe the general rules for maintaining an effective key management system?

Ans.: An effective key management system should follow certain basic rules that are defi ned as follows:

   The secret key must be stored and transmitted in a secure manner because disclosure of the secret key makes the data unsecured.

   The longer the same key is in use, the easier it becomes to crack the key. Thus, the key must be changed from time to time.

   The key must be generated randomly, so that it is hard for any attacker to guess it. The higher the randomness of the key is, higher will be the quality of the key, making it progressively more difficult to guess it.

   If the length of the key is short, its lifetime must also be short. That is, a short key must not be used for a longer period of time.

   The key must be destroyed properly after its use.

8. Briefly discuss the concept of steganography.

Ans.: Steganography, like cryptography, is a technique to implement security mechanisms. The term steganography comes from the Greek word steganos, which means “concealed writing”. Steganography is the technique of writing a message in such a way that apart from the sender and the receiver, no one will suspect the existence of the message. It enables the sender to hide a message inside another message. Although both steganography and cryptography are security mechanisms intended to protect the messages from attackers, but still they differ from each other. Where cryptography conceals the contents of a message by enciphering, steganography conceals the message itself by covering it with something.

Some of the traditional techniques of steganography include:

   Marking selected letters of a printed document with a pencil such that the marks are visible only when the document is exposed at a specific angle to bright light.

   Use of some invisible ink (such as onion juice, lemon juice, or some ammonia salt) to write a secret message such that the contents of a message are not visible until heated or some other chemical is applied.

   Use of microdots or pin punchers on selected letters such that these dots are not visible until the paper is exposed in front of a light.

Some modern techniques of steganography include hiding of a secret message within an image, audio or video file by inserting secret binary message information during the digitization process. Although the digitization process may result in an extra overhead to hide a relatively small message, it is more effective when used along with cryptography.

9. Explain Euclidean algorithm for finding the greatest common divisor.

Ans.: The Euclidean algorithm (also called Euclid's algorithm) is an efficient algorithm for finding the greatest common divisor (GCD) of two positive integers. This algorithm was invented by the Greek mathematician Euclid and is hence named after him. Given two positive integers x and y, then another positive number (say, a) is called the gcd of x and y if and only if the following conditions are satisfied:

(i) a divides both x and y.

(ii) Any other common divisor of x and y also divides a.

In other words, gcd(x,y)=a if a is the largest integer that divides both x and y.

Euclidean's algorithm computes the gcd of two positive integers, x and y, based on the following facts:

(i) gcd(x,0)=x, that is, if the second integer is zero, then the gcd is the first integer.

(ii) gcd(x,y)=gcd(y,r), where r is the remainder obtained on dividing x by y.

Algorithm

The following are the steps to find the gcd of two positive integers x and y, where x>y>0 using Euclidean's algorithm, are as follows:

1. a:=x
2. b:=y
3. while (b>0)
   {
    q:=a/b
    r:=a-q*b
    a:=b
    b:=r
   }
4. gcd(x,y):=a

In this algorithm, we have used two variables a and b to hold the remainders produced during the reduction process. To start with, variables a and b are initialized with x and y, respectively. During each step in the reduction process, we calculate the remainder of a divided by b and then store it into the variable r. Then, a and b are replaced with b and r, respectively. This process is continued until the value of b becomes zero. Eventually, we get the gcd(x, y)as a.

10. Write a short note on modular arithmetic.

Ans.: In mathematics, to perform a division operation, we need two inputs, a divisor (say, m) and a dividend (say, x). After performing the operation we get two outputs, a quotient (say, q) and a remainder (say, r). That is, the division relationship can be expressed as follows:

x=m*q+r

However, in modular arithmetic, we are interested in only one output, that is, the remainder, while the other output (that is, the quotient) is not considered. Thus, in this case, the division operation can be expressed as a binary operator having two inputs, the integers x and m and only one output r. This binary operator is referred to as the modulo operator (written as mod). The input m (divisor) to the modulo operator is referred to as the modulus, while the output r is referred to as the residue. Thus, we can say that:

x mod m=r

where x is an integer from the set of integers Z={…,-3,-2,-1,0,1,2,3,…} and the modulus (m) and residue (r) are the positive integers. In case the value of x is negative, the value of r also comes out negative. Thus, to make it non-negative, the modulus m is added to r.

11. Explain the following with reference to modular arithmetic:

(a) Set of residues

(b) Congruence

(c) Additive and multiplicative inverse

Ans.: (a) Set of residues: Consider a modulo operation x mod m=r, where x is an integer from a set of integers Z while m and r are positive integers. The result of this operation is always an integer less than m. That is, the value of r lies between 0 and m-1. Thus, it can be said that the modulo operation results in a set containing elements from 0 to m-1. In modular arithmetic, this set is called the set of least residues modulo m (denoted as Zm) or simply the set of residues. There can be infinite possible instances of Zm, one for each value of m. For example, Z11 can have 11 values {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, Z4 can have four values {0, 1, 2, 3}, and so on.

Modular arithmetic allows three binary operations: addition, subtraction, and multiplication to be applied on the elements of Zm. After applying each operation, the result obtained may need to be mapped to Zm with the help of the modulo operator. To understand, consider three elements x, y, and z such that both x and y belong to Z (or Zm) and z belongs to Zm. Then the binary operations in Zm can be expressed as (also see Figure 2.7):

(x+y) mod m=z
(x-y) mod m=z
(x*y) mod m=z

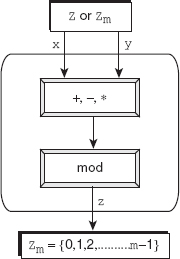
Figure 2.7 Binary operations in Z_m

(b) Congruence: There is always a many-to-one relationship between Z and Zm. That is, many elements of the set Z can map to a single element of Zm. For example, modulo operations 3 mod 10, 13 mod 10, and 23 mod 10 result in the same value (equal to 3). Thus, these numbers (3, 13, and 23) are referred to as congruent mod 10 in modular arithmetic. To represent the congruence relationship between two integers, the congruence operator represented by the ‘≡’ symbol is used. For example, we can write that 3 ≡ 13 (mod 10), 13 ≡ 23 (mod 10), and 3 ≡ 23 (mod 10).

(c) Additive and multiplicative inverse: While working with modular arithmetic, we often need to determine the inverse of an element with respect to some operation. Two commonly required inverses are additive and multiplicative inverses. The former is the inverse with respect to the addition operation, while the latter is the inverse with respect to the multiplication operation.

Each element in modular arithmetic has only one additive inverse, which is always unique; sometimes, the additive inverse of an element is the element itself. Let x and y be two elements of the set Zm. Now, x is said to be the additive inverse of y and vice versa if:

x+y≡0 (mod m)

Simply put, the additive inverse of any element, say x in Zm is equal to m-x. For example, the additive inverse of 11 in Z15={0,1,2,…,13,14} is 4 (15-11).

On the other hand, an element may or may not have a multiplicative inverse. Let x and y be two elements of the set Zm. Now, x is said to the multiplicative inverse of y and vice versa if:

x*y≡1 (mod m)

For example, the multiplicative inverse of 7 in Z15={0,1,2,…,13,14} is 13, as 7*13≡1 (mod 15).

The simple method to determine whether or not a number (x) in Zm has a multiplicative inverse is to compute the GCD of x and m. If gcd(x,m)comes out to be one, x has a multiplicative inverse; otherwise, the multiplicative inverse for x in Zm does not exist. For example, there does not exist a multiplicative inverse for number 5 in Z15 because gcd(5,15)≠ 1. Notice that if gcd(x,m)=1, x and m are said to be relatively prime.

12. Describe the extended Euclidean algorithm to find the multiplicative inverse.

Ans.: The extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the gcd of two positive integers x and y, it simultaneously finds the multiplicative inverses a and b such that:

m*x+n*y=gcd(x,y)

where m is the multiplicative inverse of x mod y and n is the multiplicative inverse of y mod x.

Algorithm

The following are the steps involved in the extended Euclidean algorithm to find the gcd of two positive integers along with the multiplicative inverses are as follows:

1. a:=x
2. b:=y
3. c:=1
4. d:=0
5. e:=0
6. f:=1
7. while (b>0)
   {
     q:=a/b

     r:=a-q*b
     a:=b
     b:=r

     m:=c-q*d
     c:=d
     d:=m

     n:=e-q*f
     e:=f
     f:=n
   }
 8. gcd(x,y):=a
 9. m:=c
10. n:=e

Similar to the Euclidean algorithm, the extended Euclidean algorithm also uses the reduction process to find the gcd and multiplicative inverses. It uses three sets of variables, (a,b), (c,d), and (e,f) and during each step of the reduction process, three sets of calculations are made, one per each set of variables. To start with, the variables a, b, c, d, e, and f are initialized with x, y, 1, 0, 0, and 1, respectively. In the while loop, variables q and r are used to hold the quotient and the remainder of a divided by b, respectively. Then, variables a and b are updated in a similar manner as in the Euclidean algorithm. The set of variables (c,d) and (e,f) are also updated on the basis of q's value. This process continues until the value of b becomes zero. Finally, we obtain the gcd(x,y) as a as well as the values of m and n.

13. What is an algebraic structure? Also, explain group, ring, and field.

Ans.: An algebraic structure refers to the combination of a set of integers and the operations that are defined on the elements of the set. The commonly used algebraic structures are as follows:

Group

A group (G), denoted as G=<{…},•>, is a set of elements along with a binary operation “•” performed on each ordered pair (x,y) of elements of G such that x•y satisfies the following four properties:

(a) Closure: If both x and y belong to the same group G, then x•y also is in G. That is, if x and y are the elements of the same group, then the result of a binary operation on these elements is another element of that group.

(b) Associativity: If x, y, and z belong to the same group G, then (x•y)•z=x•(y•z). That is, the order of operation does not affect the result.

(c) Existence of identity: For each element x in G, there always exists an identity element e within the same group such that x•e=e•x = x.

(d) Existence of inverse: For each element x in G, there always exists an inverse element x′ within the same group such that x•x′=x′•x=e.

A group that satisfies all the four properties of a group and an additional property called commutativity is said to be an abelian group, also called commutative group. The commutative property states that for all x and y belonging to G, x•y = y•x.

A group that contains a finite number of elements is referred to as a finite group, whereas a group that is not finite is called an infinite group. For example, a group G1=<{1,3,5,7,9},+> is a finite group while a group G2=<Zn,+> where Zn is a set of integers, is an infinite group. The number of elements in a group indicates the order of the group. For example, the order of group G1 is five while the order of group G2 is infinite.

Ring

A ring (R), denoted as R=<{…},•, >, is a set of elements with two binary operations, “•” and “” such that:

   R is an abelian group with respect to the first operation (•). In other words, R satisfies the closure, associativity, commutativity, existence of identity, and existence of inverse properties with respect to the “•” operation.

   R satisfies the closure and associativity properties with respect to the second operation (). In addition, the second operation () must be distributed over the first operation (•). The distributivity of the second operation over the first means that if x, b, and c are the elements of ring R, then x (y•z) = (x y) • (x z) and (x•y) z = (x z) • (y z).

A ring is said to be a commutative ring if it satisfies all the properties of a ring plus if the second operation () also satisfies the commutative property, that is for all x and y belonging to the ring R, x y=y x.

Field

A field (F), denoted as F=<{…},•,>, is a set of elements with two binary operations, “•” and “”, such that F is a commutative ring where the second operation () satisfies all the five properties defined for the first operation (•) except that there is no inverse for the identity element of the first operation with respect to the second operation.

14. Explain each finite field of the form GF(pn).

Ans.: A field with a finite number of elements is called a finite field. The finite fields are the most important and most frequently used in cryptography for performing modular arithmetic operations. The concept and theory of finite fields was given by Galois, according to which if a field is finite, then it contains pn number of elements, where p is a prime number and n is a positive integer. Thus, the finite fields are usually known as Galois field and is denoted by GF(pn).

A finite field with n=1 is called the GF(p) field. This field is in fact the set Zp={0,1,…,p-1}, in which two arithmetic operations, addition and multiplication, can be applied. Each element of this set has an additive and multiplicative inverse except zero, which has no multiplicative inverse.

As we know, positive integers are stored in computers in the form of n-bit words, where the value of n can be 8, 16, 32, and so on. This implies that the range of integers that can be stored is 0 to 2n-1 and the modulus is 2n. Now, using the GF(p) finite field with the set Zp, where p is the largest prime number less than 2n-1, would be inefficient as the integers ranging from p to 2n-1 will not be used. To overcome this inefficiency of the GF(p) field, the GF(2n) field is used. This field uses a set of 2n elements, and each element is an n-bit word.

15. Find out the result of the following operations:

(a) 140 mod 10

(b) -73 mod 13

(c) 0 mod 7

Ans.: (a) When 140 is divided by 10, we get the remainder r=0. This means that 140 mod 10=0.

(b) When -73 is divided by 13, we get the remainder r=-8. To make r non-negative, we need to add modulus (13) to r. That is, r =-8+13=5. This means that -73 mod 13=5.

(c) When 0 is divided by 7, we get the remainder r =7. This means that 0 mod 7 = 7.

16. Find the GCD of 2740 and 1760 using the Euclidean algorithm.

Ans.: Using the Euclidean algorithm as explained in Question 9, we have x = 2740 and y = 1760.

Now, initializing a = x and b = y, we get a = 2740 and b = 1760. As b > 0, we move to the first iteration of the while loop.

Algorithm

First iteration

q=2740/1760=1

r=2740-1*1760=980

a=1760

b=980

As 980 > 0, we move to the next iteration.

Second iteration

q=1760/980=1

r=1760-1*980=780

a=980

b=780

As 780 > 0, we move to the next iteration.

Third iteration

q=980/780=1

r=980-1*780=200

a=780

b=200

As 200 > 0, we move to the next iteration.

Fourth iteration

q=780/200=3

r=780-3*200=180

a=200

b=180

As 180 > 0, we move to the next iteration.

Fifth iteration

q=200/180=1

r=200-1*180=20

a=180

b=20

As 20 > 0, we move to the next iteration.

Sixth iteration

q=180/20=9

r=180-9*20=0

a=20

b=0

As the value of b has become zero, the while loop terminates.

Thus, gcd(x, y)=a

gcd(2740, 1760)=20

17. Find the greatest common divisor of 400 and 60 using the extended Euclidean algorithm. Also, find the values of m and n.

Ans.: Using the extended Euclidean algorithm as explained in Question 12, we have x = 400 and y = 60. Now, initializing a = x and b = y, we get a = 400 and b = 60. We also know that c = 1, d = 0, e = 0, and f = 1.

As b>0, we move to the first iteration of the while loop.

First iteration

q = 400/60=6

r = 400-6*60=40

a = 60

b = 40

m = 1-6*0=1

c = 0

d = 1

n = 0-6*1=-6

e = 1

f = -6

As 40 > 0, we move to the next iteration.

Second iteration

q = 60/40=1

r = 60-1*40=20

a = 40

b=20

m = 0-1*1=-1

c = 1

d = -1

n = 1-1*(-6)=7

e = -6

f = 7

As 20 > 0, we move to the next iteration.

Third iteration

q = 40/20=2

r = 40-2*20=0

a = 20

b = 0

m = 1-2*(-1)=3

c = -1

d = 3

n = (-6) -2*7=-20

e = 7

f = -20

As the value of b has become zero, the while loop terminates.

Now, gcd(x, y)=a, m = c, and n = e. Thus, gcd(400, 60)=20, m = -1, and n = 7.

Multiple-choice Questions

1.   The conversion of ciphertext into plaintext is known as __________.

(a) Encryption

(b) Decryption

(c) Cryptography

(d) Cryptanalyst

2.   Which of the following is a component of cryptography?

(a) Ciphertext

(b) Ciphers

(c) Key

(d) All of these

3.   Which of the following is needed to implement a chosen-plaintext attack?

(a) The attacker must have knowledge of the ciphertext.

(b) The attacker must have access to the receiver's computer.

(c) The attacker must have access to the sender's computer.

(d) Both (a) and (b)

4.   Which of the following is needed to implement a chosen-ciphertext attack?

(a) The attacker must have knowledge of the ciphertext.

(b) The attacker must have access to the receiver's computer.

(c) The attacker must have access to the sender's computer.

(d) Both (a) and (b)

5.   What is a chosen-text attack?

(a) It is a combination of known-plaintext attack and chosen-ciphertext attack.

(b) It is a combination of chosen-plaintext attack and known-ciphertext attack.

(c) It is a combination of known-plaintext attack and known-ciphertext attack.

(d) It is a combination of chosen-plaintext attack and chosen-ciphertext attack.

6.   Which of the following are the functions of key management?

(a) Key generation, distribution, and installation

(b) Key storage, key change, and key control

(c) Both (a) and (b)

(d) None of these

7.   Which of the following is true in the context of steganography?

(a) It conceals the existence of the message.

(b) It conceals the contents of the message.

(c) It involves less overhead than cryptography.

(d) Both (a) and (b)

8.   In public-key cryptography, __________ key is used for encryption.

(a) Public

(b) Private

(c) Both (a) and (b)

(d) Shared

9.   The multiplicative inverse of 13 in Z15 is __________.

(a) Five

(b) Seven

(c) Nine

(d) Eight

10. Which of the following properties designates a group as an abelian group?

(a) Closure

(b) Associativity

(c) Distributivity

(d) Commutativity

Answers

  1. (b)

  2. (d)

  3. (c)

  4. (d)

  5. (d)

  6. (c)

  7. (a)

  8. (a)

  9. (b)

10. (d)