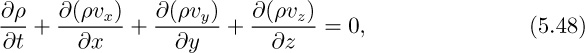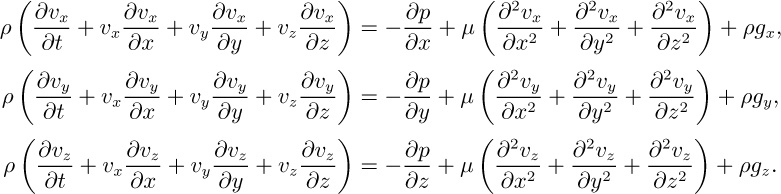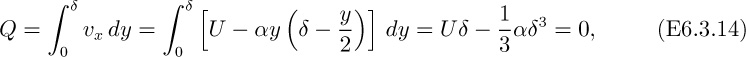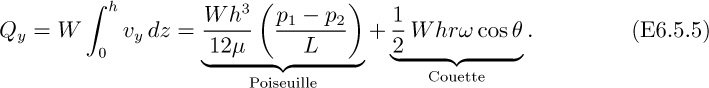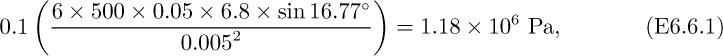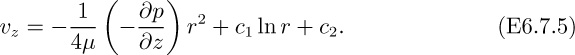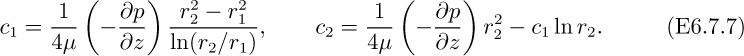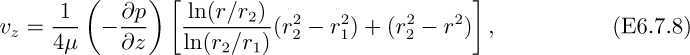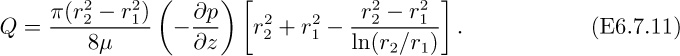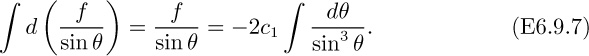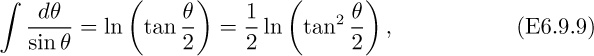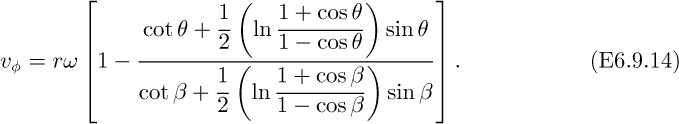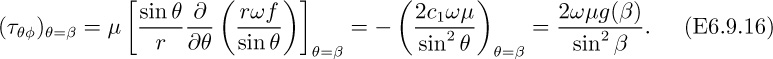Chapter 6. Solution Of Viscous-Flow Problems
6.1 Introduction
THE previous chapter contained derivations of the relationships for the conservation of mass and momentum—the equations of motion—in rectangular, cylindrical, and spherical coordinates. All the experimental evidence indicates that these are indeed the most fundamental equations of fluid mechanics, and that in principle they govern any situation involving the flow of a Newtonian fluid. Unfortunately, because of their all-embracing quality, their solution in analytical terms is difficult or impossible except for relatively simple situations. However, it is important to be aware of these “Navier-Stokes equations,” for the following reasons:
1. They lead to the analytical and exact solution of some simple, yet important problems, as will be demonstrated by examples in this chapter.
2. They form the basis for further work in other areas of chemical engineering.
3. If a few realistic simplifying assumptions are made, they can often lead to approximate solutions that are eminently acceptable for many engineering purposes. Representative examples occur in the study of boundary layers, waves, lubrication, coating of substrates with films, and inviscid (irrotational) flow.
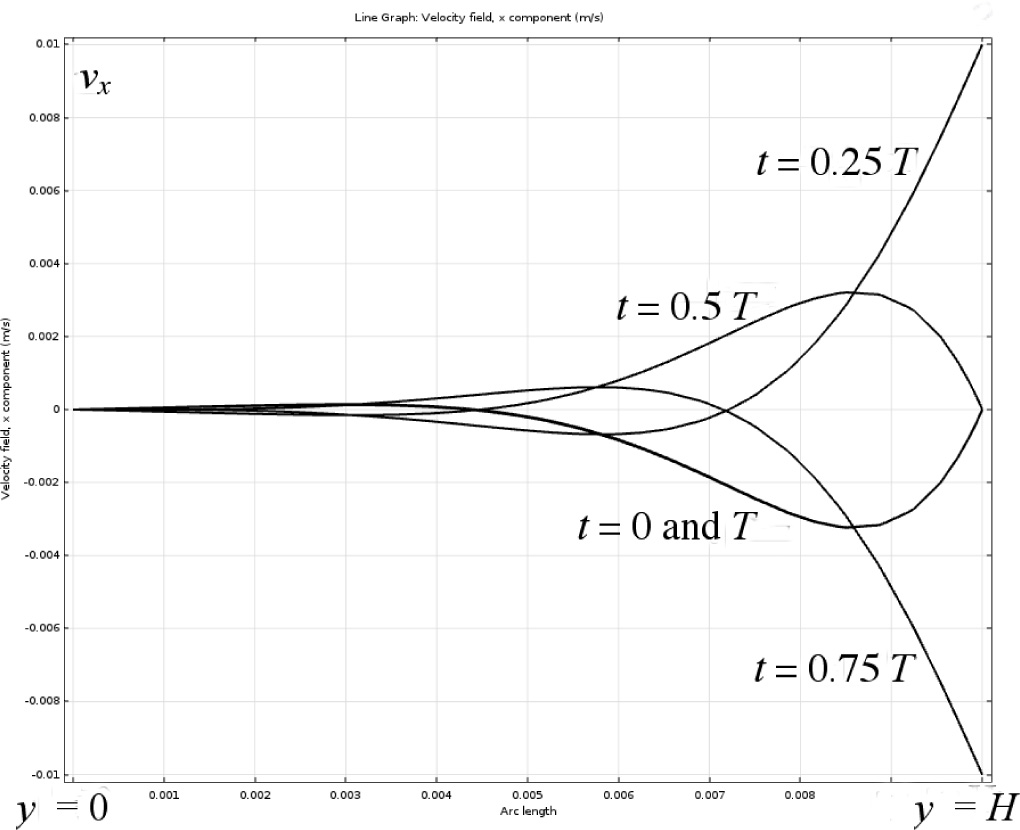
4. With the aid of more sophisticated techniques, such as those involving power series and asymptotic expansions, and particularly computer-based numerical methods (as implemented by CFD or computational fluid dynamics software such as Fluent and COMSOL), they can lead to the solution of moderately or highly advanced problems, such as those involving injection-molding of polymers and even the incredibly difficult problem of weather prediction.
The following sections present exact solutions of the equations of motion for several relatively simple problems in rectangular, cylindrical, and spherical coordinates, augmented by a couple of CFD examples. Throughout, unless otherwise stated, the flow is assumed to be steady, laminar, and Newtonian, with constant density and viscosity. Although these assumptions are necessary in order to obtain solutions, they are nevertheless realistic in several instances.
The reader is cautioned that probably a majority of industrial processes involve turbulent flow, which is more complicated, and for this reason sometimes receives scant attention in university courses. The author has seen instances in which erroneous assumptions of laminar flow have led to answers that are wildly inaccurate.
All of the examples in this chapter are characterized by low Reynolds numbers. That is, the viscous forces are much more important than the inertial forces, and are usually counterbalanced by pressure or gravitational effects. Typical applications occur in microfluidics (involving tiny channels—see Chapter 12) and in the flow of high-viscosity polymers. Situations in which viscous effects are relatively unimportant will be discussed in Chapter 7.
Solution procedure
The general procedure for solving each problem involves the following steps:
1. Make reasonable simplifying assumptions. Almost all of the cases treated here will involve steady incompressible flow of a Newtonian fluid in a single coordinate direction. Further, gravity may or may not be important, and a certain amount of symmetry may be apparent.
2. Write down the equations of motion—both mass (continuity) and momentum balances—and simplify them according to the assumptions made previously, striking out terms that are zero. Typically, only a very few terms—perhaps only one in some cases—will remain in each differential equation. The simplified continuity equation usually yields information that can subsequently be used to simplify the momentum equations.
3. Integrate the simplified equations in order to obtain expressions for the dependent variables such as velocities and pressure. These expressions will usually contain some, as yet, arbitrary constants—typically two for the velocities (since they appear in second-order derivatives in the momentum equations) and one for the pressure (since it appears only in a first-order derivative).
4. Invoke the boundary conditions in order to evaluate the constants appearing in the previous step. For pressure, such a condition usually amounts to a specified pressure at a certain location—at the inlet of a pipe, or at a free surface exposed to the atmosphere, for example. For the velocities, these conditions fall into either of the following classifications:
(a) Continuity of the velocity, amounting to a no-slip condition. Thus, the velocity of the fluid in contact with a solid surface typically equals the velocity of that surface—zero if the surface is stationary.1 And, for the few cases in which one fluid (A, for example) is in contact with another immiscible fluid (B), the velocity in fluid A equals the velocity in fluid B at the common interface.
1 In a few exceptional situations there may be lack of adhesion between the fluid and surface, in which case slip can occur. Also see Example 12.4, in which electroosmosis gives the illusion of slip.
(b) Continuity of the shear stress, usually between two fluids A and B, leading to the product of viscosity and a velocity gradient having the same value at the common interface, whether in fluid A or B. If fluid A is a liquid, and fluid B is a relatively stagnant gas, which—because of its low viscosity— is incapable of sustaining any significant shear stress, then the common shear stress is effectively zero.
5. At this stage, the problem is essentially solved for the pressure and velocities. Finally, if desired, shear-stress distributions can be derived by differentiating the velocities in order to obtain the velocity gradients; numerical predictions of process variables can also be made.
Types of flow
Two broad classes of viscous flow will be illustrated in this chapter:
1. Poiseuille flow, in which an applied pressure difference causes fluid motion between stationary surfaces.
2. Couette flow, in which a moving surface drags adjacent fluid along with it and thereby imparts a motion to the rest of the fluid.
Occasionally, it is possible to have both types of motion occurring simultaneously, as in the screw extruder analyzed in Example 6.5.
6.2 Solution of the Equations of Motion in Rectangular Coordinates
The remainder of this chapter consists almost entirely of a series of worked examples, illustrating the above steps for solving viscous-flow problems.
6.3 Alternative Solution Using a Shell Balance
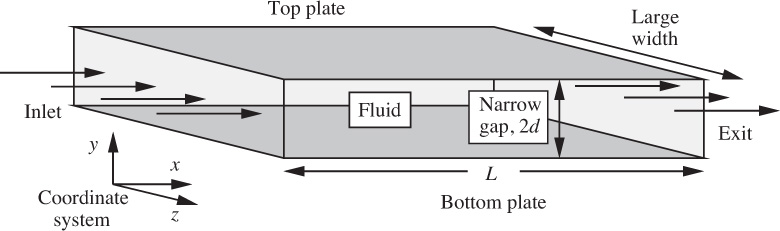
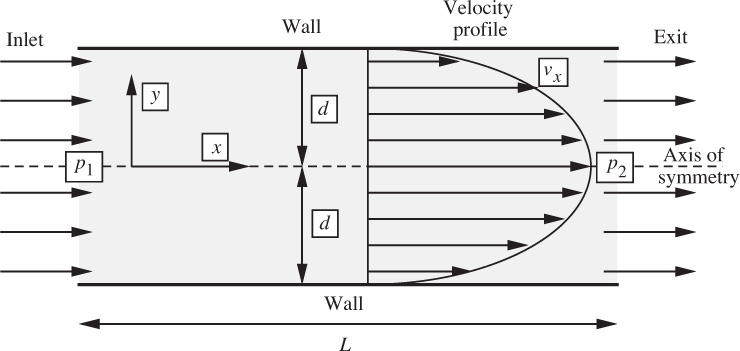
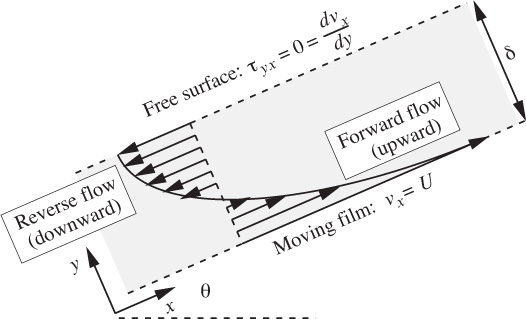
Because the flow between parallel plates was the first problem to be examined, the analysis in Example 6.1 was purposely very thorough, extracting the last “ounce” of information. In many other applications, the velocity profile and the flow rate may be the only quantities of prime importance. On the average, therefore, subsequent examples in this chapter will be shorter, concentrating on certain features and ignoring others.
The problem of Example 6.1 was solved by starting with the completely general equations of motion and then simplifying them. An alternative approach involves a direct momentum balance on a differential element of fluid—a “shell”—as illustrated in Example 6.2.
The choice of approach—simplifying the full equations of motion, or performing a shell balance—is very much a personal one, and we have generally opted for the former. The application of the Navier-Stokes equations, which are admittedly rather complicated, has the advantages of not “reinventing the (momentum balance) wheel” for each problem, and also of assuring us that no terms are omitted. Conversely, a shell balance has the merits of relative simplicity, although it may be quite difficult to perform convincingly for an element with curved sides, as would occur for the problem in spherical coordinates discussed in Example 6.8.
This section concludes with another example problem, which illustrates the application of two further boundary conditions for a liquid, one involving it in contact with a moving surface, and the other at a gas/liquid interface where there is a condition of zero shear.
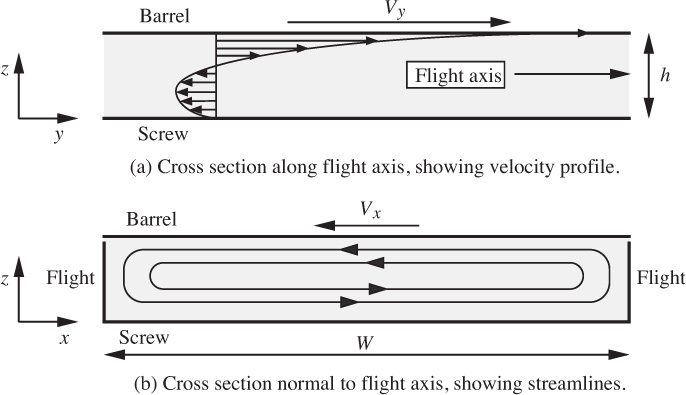
6.4 Poiseuille and Couette Flows in Polymer Processing
The study of polymer processing falls into the realm of the chemical engineer. First, the polymer, such as nylon, polystyrene, or polyethylene, is produced by a chemical reaction—either as a liquid or solid. (In the latter event, it would subsequently have to be melted in order to be processed further.) Second, the polymer must be formed by suitable equipment into the desired final shape, such as a film, fiber, bottle, or other molded object. The procedures listed in Table 6.1 are typical of those occurring in polymer processing.
Table 6.1. Typical Polymer-Processing Operations

Since polymers are generally highly viscous, their flows can be obtained by solving the equations of viscous motion. In this chapter, we cover the rudiments of extrusion, die flow, and drawing or spinning. The analysis of calendering and coating is considerably more complicated, but can be rendered tractable if reasonable simplifications, known collectively as the lubrication approximation, are made, as discussed in Chapter 8. The treatments of injection molding and blow molding are beyond the scope of this book.
Representative values
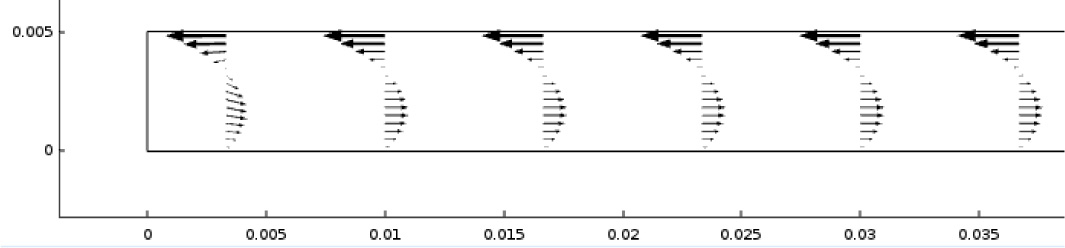
A COMSOL example follows shortly, and it is appropriate to consider typical measurements and polymer properties for screw extruders2:
2 I heartily thank Mr. John W. Ellis, who is an expert in polymer processing, for supplying these values and most of the information in Table 6.1. Mr. Ellis was previously a faculty member at the Petroleum and Petrochemical College at Chulalongkorn University in Bangkok. He is now R&D Manager at Labtech Engineering Co., Ltd, in Thailand, a company that makes laboratory-size processing machines for the plastics and rubber industries. Mr. Ellis wrote Polymer Products: Design, Materials and Processing, with co-author David Morton-Jones (Chapman and Hall, 1986). His latest book, Introduction to Plastic Foams, co-authored by Dr. Duanghathai Pentrakoon (of the Faculty of Science, Chulalongkorn University, Bangkok), was published by the Chulalongkorn University Press (2005).
1. The size of the screw varies from a laboratory diameter of 20 mm up to large production machines having diameters of 150 mm (very common) or much larger—up to 600 mm.
2. The helix angle is almost always θ = tan−1(1/π)=17.66°, corresponding to a “square thread” screw profile in which the pitch P equals the outside diameter D =2r of the screw.
3. For a 100-mm-diameter screw, a typical channel depth (metering section) would be about h = 5 or 6 mm.
4. The screw rpm ranges from a slow speed of about 30 rpm to a high speed of 150 rpm. The large extruders run at a slower rpm. A typical screw surface speed (the barrel velocity relative to the screw) for extruding polyethylene is 0.5 m/s. For a 100-mm screw, a typical screw speed would be 65 rpm.
5. The metering section length L0 depends on the type of polymer being used— amorphous, semicrystalline, etc. This length is usually expressed as a multiple of the screw diameter, such as L0 = 6.5D. Typical extruder screws have an overall length of 25D.
6. Polymers generally “shear thin” with increasing shear rate, so the viscosity will depend on the prevailing shear rate (related to rpm) of the melt in the screw channel at the melt temperature being used. But for extrusion processes we can assume a melt viscosity of anything between 200 and 1,000 N s/m2 (i.e., Pa s) for extrusion grades of polyolefins (LDPE, HDPE, and PP).
6.5 Solution of the Equations of Motion in Cylindrical Coordinates
Several chemical engineering operations exhibit symmetry about an axis z and involve one or more surfaces that can be described by having a constant radius for a given value of z. Examples are flow in pipes, extrusion of fibers, and viscometers that involve flow between concentric cylinders, one of which is rotating. Such cases lend themselves naturally to solution in cylindrical coordinates, and two examples will now be given.
6.6 Solution of the Equations of Motion in Spherical Coordinates
Most of the introductory viscous-flow problems will lend themselves to solution in either rectangular or cylindrical coordinates. Occasionally, as in Example 6.7, a problem will arise in which spherical coordinates should be used. It is a fairly advanced problem! Try first to appreciate the broad steps involved, and then peruse the fine detail at a second reading.
Problems for Chapter 6
Unless otherwise stated, all flows are steady state, for a Newtonian fluid with constant density and viscosity.
1. Stretching of a liquid film—M. In broad terms, explain the meanings of the following two equations, paying attention to any sign convention:
Fig. P6.1. Stretching of liquid film between two bars.
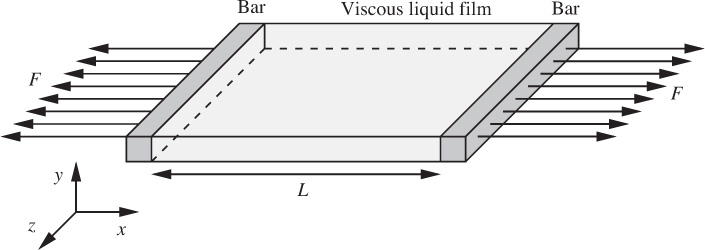
Fig. P6.1 shows a film of a viscous liquid held between two bars spaced a distance L apart. If the film thickness is uniform, and the total volume of liquid is V , show that the force necessary to separate the bars with a relative velocity dL/dt is:
Fig. P6.2. Coating of wire drawn through a die.

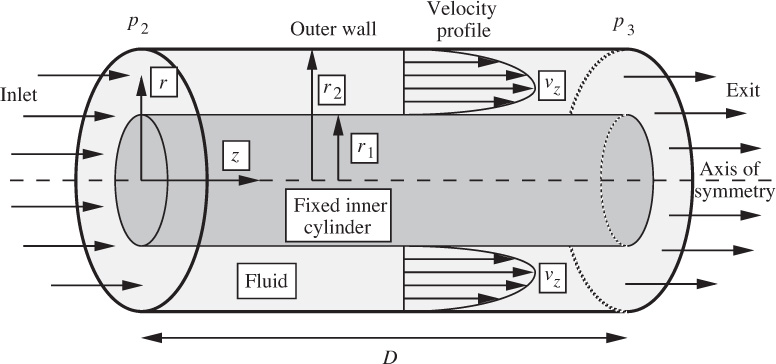
2. Wire coating—M. Fig. P6.2 shows a rodlike wire of radius r1 that is being pulled steadily with velocity V through a horizontal die of length L and internal radius r2. The wire and the die are coaxial, and the space between them is filled with a liquid of viscosity μ. The pressure at both ends of the die is atmospheric. The wire is coated with the liquid as it leaves the die, and the thickness of the coating eventually settles down to a uniform value, δ.
Neglecting end effects, use the equations of motion in cylindrical coordinates to derive expressions for:
(a) The velocity profile within the annular space. Assume that there is only one nonzero velocity component, vz, and that this depends only on radial position.
(b) The total volumetric flow rate Q through the annulus.
(c) The limiting value for Q if r1 approaches zero.
(d) The final thickness, δ, of the coating on the wire. (Here, only an equation is needed from which δ could be found.)
(e) The force F needed to pull the wire.
3. Off-center annular flow—D (C). A liquid flows under a pressure gradient ∂p/∂z through the narrow annular space of a die, a cross section of which is shown in Fig. P6.3(a). The coordinate z is in the axial direction, normal to the plane of the diagram. The die consists of a solid inner cylinder with center P and radius b inside a hollow outer cylinder with center O and radius a. The points O and P were intended to coincide, but due to an imperfection of assembly are separated by a small distance δ.
Fig. P6.3. Off-center cylinder inside a die (gap width exaggerated): (a) complete cross section; (b) effect of incrementing θ.
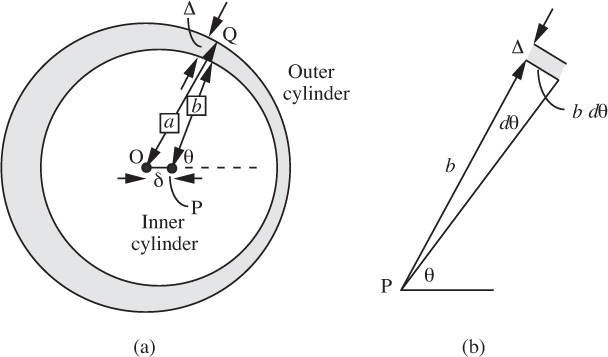
By a simple geometrical argument based on the triangle OPQ, show that the gap width Δ between the two cylinders is given approximately by:
Δ = a − b − δ cos θ,
where the angle θ is defined in the diagram.
Now consider the radius arm b swung through an angle dθ, so that it traces an arc of length bdθ. The flow rate dQ through the shaded element in Fig. P6.3(b) is approximately that between parallel plates of width bdθ and separation Δ. Hence, prove that the flow rate through the die is given approximately by:
Q = πbc(2α3 +3αδ2),
in which:
Assume from Eqn. (E6.1.26) that the flow rate per unit width between two flat plates separated by a distance h is:

What is the ratio of the flow rate if the two cylinders are touching at one point to the flow rate if they are concentric?
4. Compression molding—M. Fig. P6.4 shows the (a) beginning, (b) intermediate, and (c) final stages in the compression molding of a material that behaves as a liquid of high viscosity μ, from an initial cylinder of height H0 and radius R0 to a final disk of height H1 and radius R1.

Fig. P6.4. Compression molding between two disks.
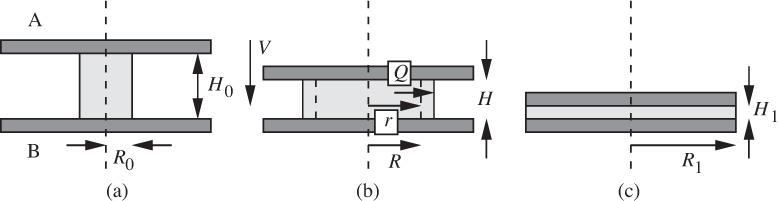
In the molding operation, the upper disk A is squeezed with a uniform velocity V toward the stationary lower disk B.
(a) Derive expressions for H and R as functions of time t, H0, and R0.
(b) Consider the radially outward volumetric flow rate Q per unit perimeter, crossing a cylinder of radius r, as in Fig. P6.4(b). Obtain a relation for Q in terms of V and r.
(c) Assume by analogy from Eqn. (E6.1.26) that per unit width of a channel of depth H, the volumetric flow rate is:
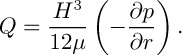
(d) Ignoring small variations of pressure in the z direction, derive an expression for the radial variation of pressure.
(e) Prove that the total compressive force F that must be exerted downward on the upper disk is:

(f) Draw a sketch that shows how F varies with time.
5. Film draining—M. Fig. P6.5 shows an idealized view of a liquid film of viscosity μ that is draining under gravity down the side of a flat vertical wall. Such a situation would be approximated by the film left on the wall of a tank that was suddenly drained through a large hole in its base.
Fig. P6.5. Liquid draining from a vertical wall.
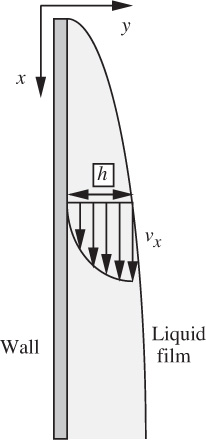
What are the justifications for assuming that the velocity profile at any distance x below the top of the wall is given by:
where h = h(x) is the local film thickness? Derive an expression for the corresponding downward mass flow rate m per unit wall width (normal to the plane of the diagram).
Perform a transient mass balance on a differential element of the film and prove that h varies with time and position according to:

Now substitute your expression for m, to obtain a partial differential equation for h. Try a solution of the form:
h = ctpxq,
and determine the unknowns c, p, and q. Discuss the limitations of your solution.
Note that a similar situation occurs when a substrate is suddenly lifted from a bath of coating fluid.
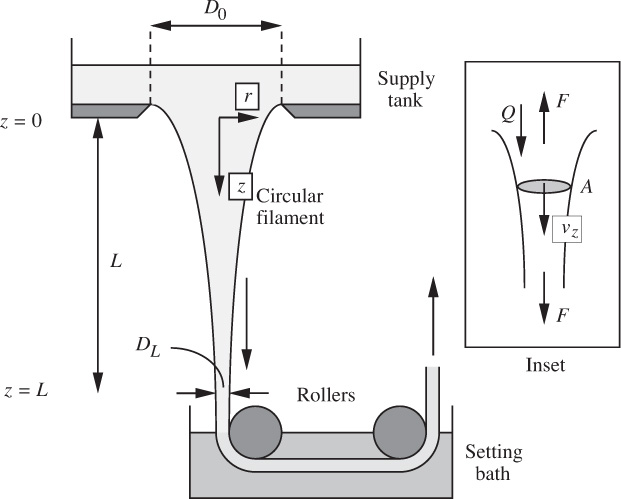
6. Sheet “spinning”—M. A Newtonian polymeric liquid of viscosity μ is being “spun” (drawn into a sheet of small thickness before solidifying by pulling it through a chemical setting bath) in the apparatus shown in Fig. P6.6.
Fig. P6.6. “Spinning” a polymer sheet.
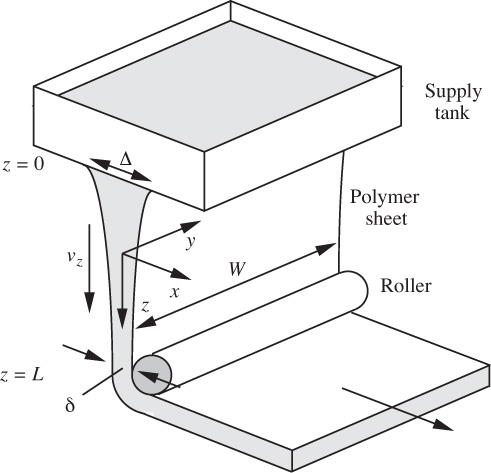
The liquid volumetric flow rate is Q, and the sheet thicknesses at z = 0 and z = L are Δ and δ, respectively. The effects of gravity, inertia, and surface tension are negligible. Derive an expression for the tensile force needed to pull the filament downward. Hint: Start by assuming that the vertically downward velocity vz depends only on z and that the lateral velocity vy is zero. Also derive an expression for the downward velocity vz as a function of z.
7. Details of pipe flow—M. A fluid of density ρ and viscosity μ flows from left to right through the horizontal pipe of radius a and length L shown in Fig. P6.7. The pressures at the centers of the inlet and exit are p1 and p2, respectively. You may assume that the only nonzero velocity component is vz, and that this is not a function of the angular coordinate, θ.
Stating any further necessary assumptions, derive expressions for the following, in terms of any or all of a, L, p1, p2, ρ, μ, and the coordinates r, z, and θ:
(a) The velocity profile, vz = vz(r).
(b) The total volumetric flow rate Q through the pipe.
(c) The pressure p at any point (r, θ, z).
(d) The shear stress, τrz.
Fig. P6.7. Flow of a liquid in a horizontal pipe.

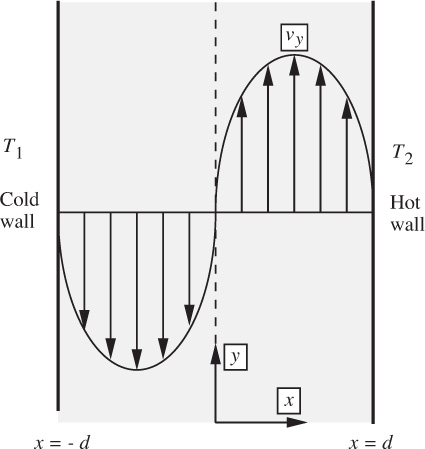
8. Natural convection—M. Fig. P6.8 shows two infinite parallel vertical walls that are separated by a distance 2d. A fluid of viscosity μ and volume coefficient of expansion β fills the intervening space. The two walls are maintained at uniform temperatures T1 (cold) and T2 (hot), and you may assume (to be proved in a heat-transfer course) that there is a linear variation of temperature in the x direction. That is:

Fig. P6.8. Natural convection between vertical walls.
The density is not constant, but varies according to:
where ![]() is the density at the mean temperature
is the density at the mean temperature ![]() , which occurs at x =0.
, which occurs at x =0.
If the resulting natural-convection flow is steady, use the equations of motion to derive an expression for the velocity profile vy = vy(x) between the plates. Your expression for vy should be in terms of any or all of x, d, T1, T2, ![]() , μ, β, and g.
, μ, β, and g.
Hints: In the y momentum balance, you should find yourself facing the following combination:

in which gy = −g. These two terms are almost in balance, but not quite, leading to a small—but important—buoyancy effect that “drives” the natural convection. The variation of pressure in the y direction may be taken as the normal hydrostatic variation:

We then have:
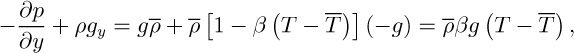
and this will be found to be a vital contribution to the y momentum balance.
9. Square duct velocity profile—M. A certain flow in rectangular Cartesian coordinates has only one nonzero velocity component, vz, and this does not vary with z. If there is no body force, write down the Navier-Stokes equation for the z momentum balance.
Fig. P6.9. Square cross section of a duct.
One-dimensional, fully developed steady flow occurs under a pressure gradient ∂p/∂z in the z direction, parallel to the axis of a square duct of side 2a, whose cross section is shown in Fig. P6.9. The following equation has been proposed for the velocity profile:
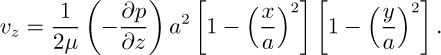
Without attempting to integrate the momentum balance, investigate the possible merits of this proposed solution for vz. Explain whether or not it is correct.
Fig. P6.10. Square cross section of a duct.
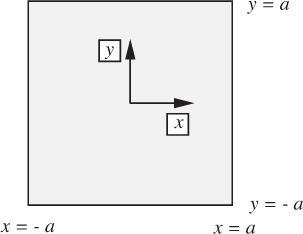
10. Poisson’s equation for a square duct—E. A polymeric fluid of uniform viscosity μ is to be extruded after pumping it through a long duct whose cross section is a square of side 2a, shown in Fig. P6.10. The flow is parallel everywhere to the axis of the duct, which is in the z direction, normal to the plane of the diagram.
If ∂p/∂z, μ, and a are specified, show that the problem of obtaining the axial velocity distribution vz = vz(x, y), amounts to solving Poisson’s equation—of the form ∇2ϕ = f(x, y), where f is specified and ϕ is the unknown. Also note that Poisson’s equation can be solved numerically by the COMSOL computational fluid dynamics program introduced in Chapter 14 (see also Example 7.4)
Fig. P6.11. Proposed velocity profiles for immiscible liquids.

11. Permissible velocity profiles—E. Consider the shear stress τyx; why must it be continuous—in the y direction, for example—and not undergo a sudden step-change in its value? Two immiscible Newtonian liquids A and B are in steady laminar flow between two parallel plates. Which—if any—of the velocity profiles shown in Fig. P6.11 are impossible? Profile A meets the interface normally in (b), but at an angle in (c). Any apparent location of the interface at the centerline is coincidental and should be ignored. Explain your answers carefully.
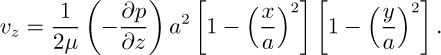
Fig. P6.12. Viscous flow past a sphere.
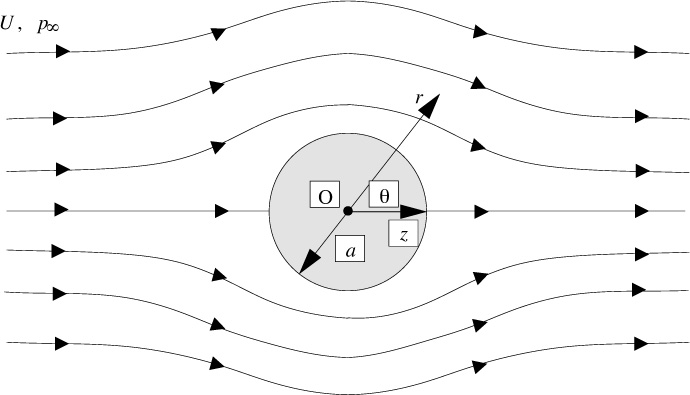
12. “Creeping” flow past a sphere—D. Figure P6.12 shows the steady, “creeping” (very slow) flow of a fluid of viscosity μ past a sphere of radius a. Far away from the sphere, the pressure is p∞ and the undisturbed fluid velocity is U in the positive z direction. The following velocity components and pressure have been proposed in spherical coordinates:
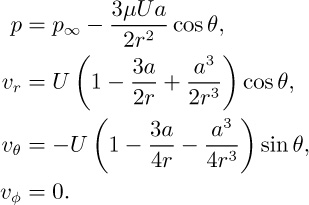
Assuming the velocities are sufficiently small so that terms such as vr(∂vr/∂r) can be neglected, and that gravity is unimportant, prove that these equations do indeed satisfy the following conditions, and therefore are the solution to the problem:
(a) The continuity equation.
(b) The r and θ momentum balances.
(c) A pressure of p∞ and a z velocity of U far away from the sphere.
(d) Zero velocity components on the surface of the sphere.
Also derive an expression for the net force exerted in the z direction by the fluid on the sphere, and compare it with that given by Stokes’ law in Eqn. (4.11).
Note that the problem is one in spherical coordinates, in which the z axis has no formal place, except to serve as a reference direction from which the angle θ is measured. There is also symmetry about this axis, such that any derivatives in the ϕ direction are zero. Note: The actual derivation of these velocities, starting from the equations of motion, is fairly difficult!
Fig. P6.13. Section of a Couette viscometer.
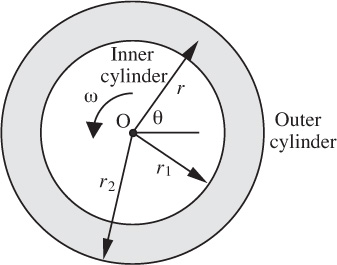
13. Torque in a Couette viscometer—M. Fig. P6.13 shows the horizontal cross section of a concentric cylinder or “Couette” viscometer, which is an apparatus for determining the viscosity μ of the fluid that is placed between the two vertical cylinders. The inner and outer cylinders have radii of r1 and r2, respectively. If the inner cylinder is rotated with a steady angular velocity ω, and the outer cylinder is stationary, derive an expression for vθ (the θ velocity component) as a function of radial location r.
If, further, the torque required to rotate the inner cylinder is found to be T per unit length of the cylinder, derive an expression whereby the unknown viscosity μ can be determined, in terms of T , ω, r1, and r2. Hint: You will need to consider one of the shear stresses given in Table 5.8.
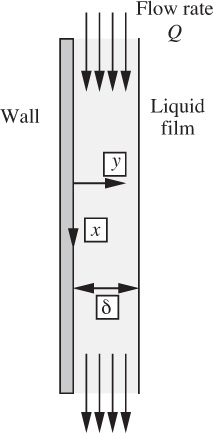
14. Wetted-wall column—M. Fig. P6.14 shows a “wetted-wall” column, in which a thin film of a reacting liquid of viscosity μ flows steadily down a plane wall, possibly for a gas-absorption study. The volumetric flow rate of liquid is specified as Q per unit width of the wall (normal to the plane of the diagram).
Assume that there is only one nonzero velocity component, vx, and that this does not vary in the x direction, and that the gas exerts negligible shear stress on the liquid film. Starting from the equations of motion, derive an expression for the “profile” of the velocity vx (as a function of ρ, μ, g, y, and δ), and also for the film thickness, δ (as a function of ρ, μ, g, and Q).
Fig. P6.14. Wetted-wall column.
15. Simplified view of a Weissenberg rheogoniometer—M. Consider the Weissenberg rheogoniometer with a very shallow cone; thus, referring to Fig. E6.9, β = π/2 − α, where α is a small angle.
(a) Without going through the complicated analysis presented in Example 6.9, outline your reasons for supposing that the shear stress at any location on the cone is:
(b) Hence, prove that the torque required to hold the cone stationary (or to rotate the lower plate) is:

(c) By substituting β = π/2 − α into Eqn. (E6.9.13) and expanding the various functions in power series (only a very few terms are needed), prove that g(β)= 1/(2α), and that Eqn. (E6.9.18) again leads to the expression just obtained for the torque in part (b) above.
16. Parallel-disk rheometer—M. Fig. P6.16 shows the diametral cross section of a viscometer, which consists of two opposed circular horizontal disks, each of radius R, spaced by a vertical distance H; the intervening gap is filled by a liquid of constant viscosity μ and constant density. The upper disk is stationary, and the lower disk is rotated at a steady angular velocity ω in the θ direction.
Fig. P6.16. Cross section of parallel-disk rheometer.

There is only one nonzero velocity component, vθ, so the liquid everywhere moves in circles. Simplify the general continuity equation in cylindrical coordinates, and hence deduce those coordinates (r?, θ?, z?) on which vθ may depend.
Now consider the θ-momentum equation, and simplify it by eliminating all zero terms. Explain briefly: (a) why you would expect ∂p/∂θ to be zero, and (b) why you cannot neglect the term ∂2vθ/∂z2.
Also explain briefly the logic of supposing that the velocity in the θ direction is of the form vθ = rωf(z), where the function f(z) is yet to be determined. Now substitute this into the simplified θ-momentum balance and determine f(z), using the boundary conditions that vθ is zero on the upper disk and rω on the lower disk.
Why would you designate the shear stress exerted by the liquid on the lower disk as τzθ? Evaluate this stress as a function of radius.
17. Screw extruder optimum angle—M. Note that the flow rate through the die of Example 6.7, given in Eqn. (E6.7.11), can be expressed as:
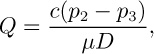
in which c is a factor that accounts for the geometry.
Suppose that this die is now connected to the exit of the extruder studied in Example 6.5, and that p1 = p3 = 0, both pressures being atmospheric. Derive an expression for the optimum flight angle θopt that will maximize the flow rate Qy through the extruder and die. Give your answer in terms of any or all of c, D, h, L0, r, W , μ, and ω.
For what value of c would the pressure at the exit of the extruder approach its largest possible value p2max? Derive an expression for p2max.
18. Annular flow in a die—E. Referring to Example 6.7, concerning annular flow in a die, answer the following questions, giving your explanation in both cases:
(a) What form does the velocity profile, vz = vz(r), assume as the radius r1 of the inner cylinder becomes vanishingly small?
(b) Does the maximum velocity occur halfway between the inner and outer cylinders, or at some other location?
19. Rotating rod in a fluid—M. Fig. P6.19(a) shows a horizontal cross section of a long vertical cylinder of radius a that is rotated steadily counter-clockwise with an angular velocity ω in a very large volume of liquid of viscosity μ. The liquid extends effectively to infinity, where it may be considered at rest. The axis of the cylinder coincides with the z axis.
Fig. P6.19. Rotating cylinder in (a) a single liquid, and (b) two immiscible liquids.
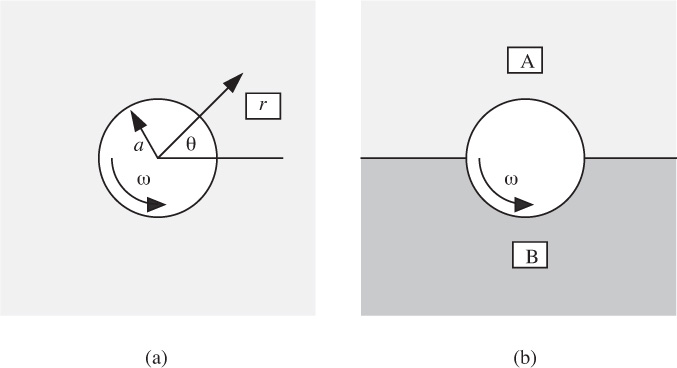
(a) What type of flow is involved? What coordinate system is appropriate?
(b) Write down the differential equation of mass and that one of the three general momentum balances that is most applicable to the determination of the velocity vθ.
(c) Clearly stating your assumptions, simplify the situation so that you obtain an ordinary differential equation with vθ as the dependent variable and r as the independent variable.
(d) Integrate this differential equation, and introduce any boundary condition(s), and prove that vθ = ωa2/r.
(e) Derive an expression for the shear stress τrθ at the surface of the cylinder. Carefully explain the plus or minus sign in this expression.
(f) Derive an expression that gives the torque T needed to rotate the cylinder, per unit length of the cylinder.
(g) Derive an expression for the vorticity component (∇ × v)z. Comment on your result.
(h) Fig. P6.19(b) shows the initial condition of a mixing experiment in which the cylinder is in the middle of two immiscible liquids, A and B, of identical densities and viscosities. After the cylinder has made one complete rotation, draw a diagram that shows a representative location of the interface between A and B.
Fig. P6.20. Two-phase flow between parallel plates.
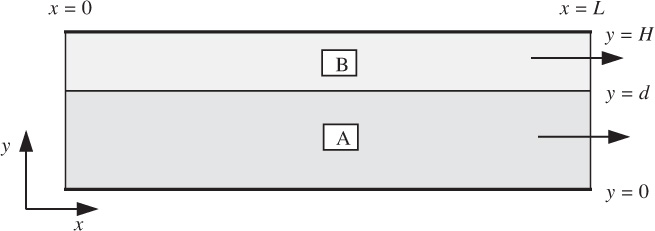
20. Two-phase immiscible flow—M. Fig. P6.20 shows an apparatus for measuring the pressure drop of two immiscible liquids as they flow horizontally between two parallel plates that extend indefinitely normal to the plane of the diagram. The liquids, A and B, have viscosities μA and μB, densities ρA and ρB, and volumetric flow rates QA and QB (per unit depth normal to the plane of the figure), respectively. Gravity may be considered unimportant, so that the pressure is essentially only a function of the horizontal distance, x.
(a) What type of flow is involved?
(b) Considering layer A, start from the differential equations of mass and momentum, and, clearly stating your assumptions, simplify the situation so that you obtain a differential equation that relates the horizontal velocity vxA to the vertical distance y.
(c) Integrate this differential equation so that you obtain vxA in terms of y and any or all of d, dp/dx, μA, ρA, and (assuming the pressure gradient is uniform) two arbitrary constants of integration, say, c1A and c2A. Assume that a similar relationship holds for vxB.
(d) Clearly state the four boundary and interfacial conditions, and hence derive expressions for the four constants, thus giving the velocity profiles in the two layers.
(e) Sketch the velocity profiles and the shear-stress distribution for τyx between the upper and lower plates.
(f) Until now, we have assumed that the interface level y = d is known. In reality, however, it will depend on the relative flow rates QA and QB. Show clearly how this dependency could be obtained, but do not actually carry the analysis through to completion.
Fig. P6.21. Rotating-impeller humidifier.
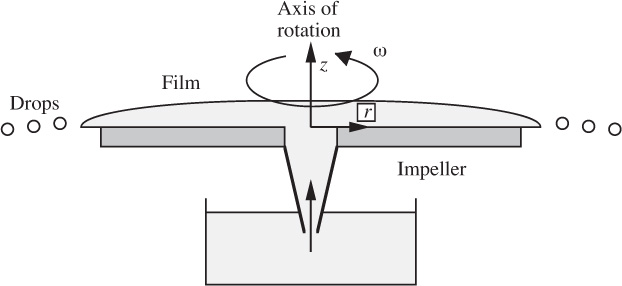
21. Room humidifier—M. Fig. P6.21 shows a room humidifier, in which a circular impeller rotates about its axis with angular velocity ω. A conical extension dips into a water-bath, sucking up the liquid (of density ρ and viscosity μ), which then spreads out over the impeller as a thin laminar film that rotates everywhere with an angular velocity ω, eventually breaking into drops after leaving the periphery.
(a) Assuming incompressible steady flow, with symmetry about the vertical (z) axis, and a relatively small value of vz, what can you say from the continuity equation about the term:
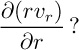
(b) If the pressure in the film is everywhere atmospheric, the only significant inertial term is ![]() , and information from (a) can be used to neglect one particular term, to what two terms does the r momentum balance simplify?
, and information from (a) can be used to neglect one particular term, to what two terms does the r momentum balance simplify?
(c) Hence prove that the velocity vr in the radial direction is a half-parabola in the z direction.
(d) Derive an expression for the total volumetric flow rate Q, and hence prove that the film thickness at any radial location is given by:
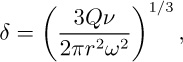
where ν is the kinematic viscosity.
Fig. P6.22. Transport of inner cylinder.

22. Transport of inner cylinder—M (C). As shown in Fig. P6.22, a long solid cylinder of radius rc and length L is being transported by a viscous liquid of the same density down a pipe of radius a, which is much smaller than L. The annular gap, of extent a − rc, is much smaller than a. Assume: (a) the cylinder remains concentric within the pipe, (b) the flow in the annular gap is laminar, (c) the shear stress is essentially constant across the gap, and (d) entry and exit effects can be neglected. Prove that the velocity of the cylinder is given fairly accurately by:

where Q is the volumetric flow rate of the liquid upstream and downstream of the cylinder. Hint: Concentrate first on understanding the physical situation. Don’t rush headlong into a lengthy analysis with the Navier-Stokes equations!
Fig. P6.23. Flow between inclined planes.

23. Flow between inclined planes—M (C). A viscous liquid flows between two infinite planes inclined at an angle 2α to each other. Prove that the liquid velocity, which is everywhere parallel to the line of intersection of the planes, is given by:
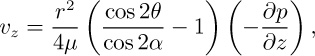
where z, r, θ are cylindrical coordinates. The z axis is the line of intersection of the planes and the r axis at θ = 0 bisects the angle between the planes. Assume laminar flow, with:
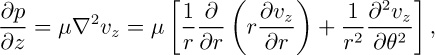
and start by proposing a solution of the form vz = rng(θ)(−∂p/∂z)/μ, where the exponent n and function g(θ) are to be determined.
Fig. P6.24. Flow of two immiscible liquids in a pipe. The thickness Δ of the film next to the wall is exaggerated.
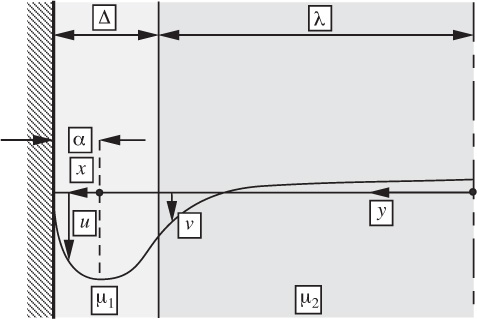
24. Immiscible flow inside a tube—D (C). A film of liquid of viscosity μ1 flows down the inside wall of a circular tube of radius (λ + Δ). The central core is occupied by a second immiscible liquid of viscosity μ2, in which there is no net vertical flow. End effects may be neglected, and steady-state circulation in the core liquid has been reached. If the flow in both liquids is laminar, so that the velocity profiles are parabolic as shown in Fig. P6.24, prove that:

where Δ is the thickness of the liquid film, and α is the distance from the wall to the point of maximum velocity in the film. Fig. P6.24 suggests notation for solving the problem. To save time, assume parabolic velocity profiles without proof: u = a + bx + cx2 and v = d + ey + fy2.
Discuss what happens when λ/Δ → ∞; and also when μ2/μ1 → 0; and when μ1/μ2 → 0.
25. Blowing a polyethylene bubble—D. For an incompressible fluid in cylindrical coordinates, write down:
(a) The continuity equation, and simplify it.
(b) Expressions for the viscous normal stresses σrr and σθθ, in terms of pressure, viscosity, and strain rates.
Fig. P6.25. Cross section of half of a cylindrical bubble.

A polyethylene sheet is made by inflating a cylindrical bubble of molten polymer effectively at constant length, a half cross section of which is shown in Fig. P6.25. The excess pressure inside the bubble is small compared with the external pressure P , so that Δp ≪ P and σrr . = −P .
By means of a suitable force balance on the indicated control volume, prove that the circumferential stress is given by σθθ = −P + aΔp/t. Assume pseudo-steady state—that is, the circumferential stress just balances the excess pressure, neglecting any acceleration effects.
Hence, prove that the expansion velocity vr of the bubble (at r = a) is given by:

and evaluate it for a bubble of radius 1.0 m and film thickness 1 mm when subjected to an internal gauge pressure of Δp = 40 N/m2. The viscosity of polyethylene at the appropriate temperature is 105 N s/m2.
26. Surface-tension effect in spinning—M. Example 6.8 ignored surface-tension effects, which would increase the pressure in a filament of radius R approximately by an amount σ/R, where σ is the surface tension. Compare this quantity with the reduction of pressure, μdvz/dz, caused by viscous effects, for a polymer with μ =104 P, σ =0.030 kg/s2, L =1 m, RL (exit radius) = 0.0002 m, vz0 =0.02 m/s, and vzL = 2 m/s. Consider conditions both at the beginning and end of the filament. Comment briefly on your findings.
27. Radial pressure variations in spinning—M. Example 6.8 assumed that the variation of pressure across the filament was negligible. Investigate the validity of this assumption by starting with the suitably simplified momentum balance:

If vz is the local axial velocity, prove that the corresponding increase of pressure from just inside the free surface (pR) to the centerline (p0) is:

where β = vzL/vz0. Obtain an expression for the ratio ξ =(pR − p0)/(μdvz/dz), in which the denominator is the pressure decrease due to viscosity when crossing the interface from the air into the filament, and which was accounted for in Example 6.6.
Estimate ξ at the beginning of the filament for the situation in which μ =104 P, L = 1 m, RL (exit radius) = 0.0002 m, vz0 = 0.02 m/s, and vzL = 2 m/s. Comment briefly on your findings.
28. Condenser with varying viscosity—M. In a condenser, a viscous liquid flows steadily under gravity as a uniform laminar film down a vertical cooled flat plate. Due to conduction, the liquid temperature T varies linearly across the film, from T0 at the cooled plate to T1 at the hotter liquid/vapor interface, according to T = T0 + y(T1 − T0)/h. The viscosity of the liquid is given approximately by μ = μ*(1 − αT ), where μ* and α are constants.
Prove that the viscosity at any location can be reexpressed as:
where μ0 and μ1 are the viscosities at temperatures T0 and T1, respectively.
What is the expression for the shear stress τyx for a liquid for steady flow in the x direction? Derive an expression for the velocity vx as a function of y. Make sure that you do not base your answer on any equations that assume constant viscosity.
Sketch the velocity profile for both a small and a large value of α.
29. Rotating sphere—M. A sphere of radius R, immersed in a liquid of viscosity μ of infinite extent, rotates about its z axis (see Fig. 5.9(b)) with a steady angular velocity ω in the ϕ direction. You may assume that the only nonzero liquid velocity component is that in the ϕ direction, and is of the form vϕ = c sin θ/r2.
(a) Verify that the proposed form for vϕ satisfies the appropriate momentum balance, and determine c in terms of R and ω.
(b) Prove that the shear stress at any radial location in the liquid is τrϕ = −3μc sin θ/r3, and carefully explain the minus sign.
(c) Obtain an expression for the torque T needed to rotate the sphere, as a function of R, ω, and μ. You should need the indefinite integral:

30. Moving plate—M. Similar to the first part of Example 6.4, consider a viscous fluid of infinite extent and kinematic viscosity ν with a long flat plate in its surface. At t = 0, the plate suddenly starts moving with a steady velocity vx0 in the x direction. Prove, by checking ∂vx/∂t = ν∂2vx/∂z2 and the boundary conditions, that the fluid velocity at a depth z is subsequently given by:
You may assume that:
31. Oscillating plate—M. Similar to the second part of Example 6.4, consider a viscous fluid of infinite extent and kinematic viscosity ν with a long flat plate in its surface. The plate oscillates backwards and forwards in the x direction with velocity vx0 = a sin ωt. After any initial transients have died out, prove, by checking ∂vx/∂t = ν∂2vx/∂z2 and the boundary conditions, that the fluid velocity at a depth z is subsequently given by:
in which
32. True/false. check true or false, as appropriate:
(a) For horizontal flow of a liquid in a rectangular duct between parallel plates, the pressure varies linearly both in the direction of flow and in the direction normal to the plates.
T ![]() F
F ![]()
(b) For horizontal flow of a liquid in a rectangular duct between parallel plates, the boundary conditions can be taken as zero velocity at one of the plates and either zero velocity at the other plate or zero velocity gradient at the centerline.
T ![]() F
F ![]()
(c) For horizontal flow of a liquid in a rectangular duct between parallel plates, the shear stress varies from zero at the plates to a maximum at the centerline.
T ![]() F
F ![]()
(d) For horizontal flow of a liquid in a rectangular duct between parallel plates, a measurement of the pressure gradient enables the shear-stress distribution to be found.
T ![]() F
F ![]()
(e) In fluid mechanics, when integrating a partial differential equation, you get one or more constants of integration, whose values can be determined from the boundary condition(s).
T ![]() F
F ![]()
(f) For flows occurring between r = 0 and r = a in cylindrical coordinates, the term ln r may appear in the final expression for one of the velocity components.
T ![]() F
F ![]()
(g) For flows in ducts and pipes, the volumetric flow rate can be obtained by differentiating the velocity profile.
T ![]() F
F ![]()
(h) Natural convection is a situation whose analysis depends on not taking the density as constant everywhere.
T ![]() F
F ![]()
(i) A key feature of the Weissenberg rheogoniometer is the fact that a conical upper surface results in a uniform velocity gradient between the cone and the plate, for all values of radial distance.
T ![]() F
F ![]()
(j) If, in three dimensions, the pressure obeys the equation ∂p/∂y = −ρg, and both ∂p/∂x and ∂p/∂z are nonzero, then integration of this equation gives the pressure as p = −ρgy + c, where c is a constant.
T ![]() F
F ![]()
(k) If two immiscible liquids A and B are flowing in the x direction between two parallel plates, both the velocity vx and the shear stress τyx are continuous at the interface between A and B, where the coordinate y is normal to the plates.
T ![]() F
F ![]()
(l) In compression molding of a disk between two plates, the force required to squeeze the plates together decreases as time increases.
T ![]() F
F ![]()
(m) For flow in a wetted-wall column, the pressure increases from atmospheric pressure at the gas/liquid interface to a maximum at the wall.
T ![]() F
F ![]()
(n) For one-dimensional flow in a pipe—either laminar or turbulent—the shear stress τrz varies linearly from zero at the wall to a maximum at the centerline.
T ![]() F
F ![]()
(o) In Example 6.1, for flow between two parallel plates, the shear stress τyx is negative in the upper half (where y > 0), meaning that physically it acts in the opposite direction to that indicated by the convention.
T ![]() F
F ![]()