Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

A
Appendix

A.1 Algebra and Matrix Theory

We now present some inequalities on vector and matrix norms. Consider vector and matrix . Define , , , and , where with matrix eigenvalues.

Since the matrix norm is induced by the corresponding vector norm, we have

(A.1) $images$

For matrix , we have the following inequality

(A.2) $images$

Hints: Inequalities (A.1) and (A.2) are frequently used. In Section 5.2.4, for instance, they are used to derive equations (5.44) and (5.47).

A.2 Systems and Control Theory

A.2.1 Definitions of Lipschitz Condition

Consider the state of the linear time‐invariant equation

(A.6) $images$

where is the state, is the control input, and matrices and .

The solution to (A.6) is given by

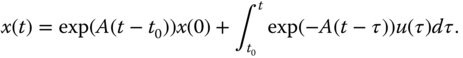
(A.7) $images$

A.2.2 Definitions of Asymptotically Stable

Consider the autonomous system

(A.10) $images$

where is a locally Lipschitz map from a domain into . Let be an equilibrium point for (A.10). Then

the equilibrium point is said to be stable if, for any 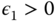, there exists such that if 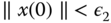, then 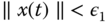for all ;
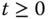the equilibrium point is asymptotically stable if it is stable, and if there additionally exists some 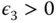such that implies that as ;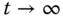
the equilibrium point 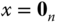is exponentially stable if there exist two strictly positive numbers, and 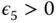, such that
(A.11) $images$
in some ball around the origin 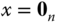. If the stability of the equilibrium point holds for all initial states, 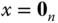is said to be globally stable. The equilibrium point 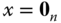is globally asymptotically stable (respectively, globally exponentially stable) when is asymptotically stable (respectively, exponentially stable) for all initial states.

A.2.3 Definitions of Input‐to‐state Stability

A.2.4 Bounds of Solutions of Linear Systems

Lyapunov analysis will be used to show the boundedness and ultimate bound of solutions of some disturbed state equations. A useful lemma is as follows.

Proof

View system (A.14) as a perturbation of the unforced system . Point 1 can be obtained by directly applying Lemma 4.6 from Khalil et al. [3]. In fact, it is easy to check that all conditions of this lemma are trivially satisfied by system (A.14) since:

the term is continuously differentiable and globally Lipschitz in ;
with Hurwitz marix has a globally exponentially stable equilibrium point at the origin .

To show point 2, consider the Lyapunov function

(A.18) $images$

which obviously satisfies the inequalities

(A.19) $images$

The first‐order time derivative of along the trajectories of (A.14) is given by

(A.20) $images$

Clearly, with any ,

(A.21) $images$

Furthermore,

(A.22) $images$

where with .

Take and (with small abuse of the symbols and ). Because and are functions, all conditions of Theorem 4.18 in Khalil et al. [3] (i.e., inequalities (4.39) and (4.40) therein) are globally satisfied. Applying this theorem directly to system (A.14) gives point 2.

By applying the above lemma to some lower‐order linear system, it is easy to derive some important properties concerning the bounds of the solution of these systems. For instance, we first consider the following first‐order linear equation:

(A.23) $images$

where is a positive constant, and .

A.2.5 Results for Small‐signal Stability

Consider the system

(A.29) $images$

(A.30) $images$

where , , , is piecewise continuous in and locally Lipschitz in , is piecewise continuous in and continuous in , is a domain that contains , and is a domain containing the point . For each fixed , the state model given by (A.29) and (A.30) defines an operator that assigns to each input signal the corresponding output signal . Suppose is an equilibrium point of the unforced system

(A.31) $images$

Generalized saturation functions are used in control design. They are defined as follows.

A.3 Proofs

A.3.1 Proof of Theorem 5.6

A.3.2 Proof of Lemma 5.10

Proof

To prove the first statement, consider the Lyapunov function candidate

(A.43) $images$

for each , which is positive definite and radially unbounded with respect to and due to (A.39). Differentiating along the trajectories of (5.57), gives

$images$

where the odd property of is used. Thus, and are bounded for all under any initial condition.

Noting implies , we obtain by LaSalle's invariance principle. Since the condition of the Barbalat lemma is satisfied ( is obviously bounded), we obtain . As a result, due to (5.57). This completes the proof of the first statement.

The second statement is an immediate result of the first statement due to the properties of the Type III LSEs. Let , , and . Then, the nominal control vector satisfies and

(A.44) $images$

which further shows that is unique and bounded since both and are bounded under the considered conditions. Applying (A.1) to (A.44) and considering the parameter condition (5.59), yields

(A.45) $images$

Now, the third statement is clear since .

A.3.3 Proof of Lemma 5.13

Proof

We aim to show the small‐signal stability of system (5.60) by applying Lemma A.14. The proof is then reduced to checking that all the conditions of the lemma are satisfied. For each , we use and to denote the system state and output, respectively. Then, the second‐order equation included in (5.60) can be rewritten into

(A.46) $images$

where

(A.47) $images$

The Jacobian matrices are given by

(A.48) $images$

By property P3 of saturation functions, is continuously differentiable and the Jacobian matrices and are bounded uniformly in . Moreover,

(A.49) $images$

in any neighborhood of ( , ). Note that is a globally uniformly asymptotically stable equilibrium point of the unforced system (5.57). Thus, all the conditions of Lemma A.14 are satisfied and the second‐order equation included in (5.60) is small‐signal stable. This easily ensures that the third‐order system (5.60) is also small‐signal stable.

We here apply Lemma A.13 to the system to show it is also LISS. The proof is reduced to checking that all the conditions of Lemma A.13 are satisfied. Since the system clearly satisfies the conditions of the converse Lyapunov theorem (i.e., Theorem 4.16 in Khalil et al. [3]), there exists a Lyapunov function satisfying the inequalities (A.32)–(A.34). Moreover, all the other conditions of Lemma A.13 (i.e., (A.35)–(A.36)) also hold since and . Thus, all the results included in Lemma A.13 hold. So, similar to (A.37), the inequality

(A.50) $images$

holds for any and , where is equivalent to in Lemma A.13, and , and have the same meanings as in Lemma A.13.

Since the unforced system (5.57) is globally asymptotically stable, can be arbitrarily large. Because the mapping from to is causal, depends only on for . Thus, the supremum on the right‐hand side of (A.50) can be taken over . Thus,

(A.51) $images$

for and , which implies that the second‐order equation included in (5.60) is LISS by definition. This ends the proof of Lemma 5.13.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Appendix A

Create new playlist

Sign In

Sign Up

A.1 Algebra and Matrix Theory

A.2 Systems and Control Theory

A.2.1 Definitions of Lipschitz Condition

A.2.2 Definitions of Asymptotically Stable

A.2.3 Definitions of Input‐to‐state Stability

A.2.4 Bounds of Solutions of Linear Systems

A.2.5 Results for Small‐signal Stability

A.3 Proofs

A.3.1 Proof of Theorem 5.6

A.3.2 Proof of Lemma 5.10

A.3.3 Proof of Lemma 5.13

Table of Contents for
Appendix A