13.1.1 Description of the contract

Universal life is a type of contract that began in the 1970s, and now accounts for a substantial portion of life insurance sales. Prior to that time, the mainstay of life insurance was for the most part whole life or endowment contracts. The origin of the change could well have been the advice given by some financial advisors that people should buy term insurance instead of those products, for a much smaller premium, and then invest the difference elsewhere. Now our analysis in Section 6.4.2 shows that this is exactly what happens within the policy itself when one purchases whole life or endowment insurance. The excess premiums, not needed to provide insurance in a particular year, are invested in the savings portion. Of course, the purchaser of endowment or whole life insurance has less flexibility than the term buyer, both with regards to the relative amounts going into the insurance and savings portion, and to the types of investments and rates of return. Universal life plans were developed to allow this flexibility within a single contract. The main features involve variable premium payments, and the ability for the policyholder to participate in higher yielding investment opportunities.

In the usual type of universal life plan, premiums are not fixed in advanced and may be varied at the option of the purchaser. Each individual has in effect a separate fund that changes over time in the way we describe it by the recursion formula (6.6). Premiums paid are deposited, the fund is credited with interest or investment earnings, while expenses, and the cost of insurance, based on the net amount at risk are deducted. The policyholder need only pay sufficient premiums to ensure that the fund value will cover the cost of insurance.

In this type of plan where there is a more direct relationship between policyholders and their individual accounts, there is a more frequent demand for the type of plan that we discussed in Section 6.7. It is usual to allow two options. The purchaser can fix the amount paid at death, or they can fix the net amount at risk, so at death, the amount in their account (representing the reserve) would be returned in addition to the stipulated face amount, giving an increasing death benefit. In the usual terminology the fixed death benefit is often referred to as a Type A policy, whereas the death benefit plus account value is referred to as type B.

Some plans provide the flexibility to alter the face amount as well as the premium, with the stipulation that a request to increase the coverage would normally necessitate the type of information as required by new policyholders as to health and other conditions affecting the risk. There do arise cases however when such changes are mandated. In the United States this occurs due to regulations stipulating that in order to receive the favourable tax treatment accorded to life insurance, the death benefit must exceed the fund value by a certain minimum percentage. If the fund value gets high enough, the insurer will increase the death benefit in order to maintain this so-called corridor requirement.

Policyholders can lapse the policy at any time and receive their fund value less a so-called surrender charge that is intended mainly to account for the initial expenses, as we outlined in Section 6.6. The surrender charge will decrease with time and normally will become zero after a certain number of years, often 20 or so.

As well as the flexibility in premium payments a major attraction of universal life for the purchaser is the opportunity to earn a higher yield. The credited interest rate is usually not fixed in advance as it essentially is in traditional plans, but it is allowed to vary. There are different ways of accomplishing this. In some cases the funds of the policyholder are actually invested in certain assets, so that the account is very much like a mutual fund investment together with guaranteed benefits payable on death. Usually there is a choice of various types of assets or funds to invest in, so the policyholder can control the amount of risk they are willing to take in order to obtain higher returns. This type of contract is often referred to as variable universal life. In other cases the account of the policyholder need not be invested in any particular assets but interest is credited according to earnings on some reference portfolio. Such contracts are known as equity indexed insurance. There are normally some qualifications to the crediting of interest. There will be a stipulated minimum rate of interest that is credited regardless of what the reference portfolio does. It is also common to have limits on the other end. There may be a ‘participation rate’. So for example if the reference portfolio earned 9% interest over a period and the participation rate was 80%, the the policyholder’s account would be credited with 7.2%. In addition there is often a stated maximum that will be credited regardless of the actual earnings.

Universal life contracts often carry other guarantees that mitigate again unfavourable investment experience. These are referred to as secondary guarantees. A popular option of this type, is that as long as the insured keeps up a certain stipulated minimum rate of premium payment, the death benefit is guaranteed even though lower than expected rates of return bring the person’s account below the amount needed to meet the costs of insurance. A similar provision is commonly used with endowment type contracts that have a maturity date, in which case a minimum guaranteed amount paid at maturity provided that the insured keeps up a minimum schedule of premium payments.

13.1.2 Calculating account values

For each policyholder, the amount of money in their account is calculated periodically, often monthly. For the most part this is handled easily by the basic recursion formulas that we have seen in previous chapters. There are however some aspects of terminology and special features that will be discussed. Given the account value AV_k at time k, the account value AV_{k + 1} is calculated using the following familiar quantities. We assume aggregate mortality and payment of benefits at the end of the period of death.

1. π_k, the premium paid at time k.
2. r_k, the premium expense rate. This is a percentage, often around 5%, taken from each premium by the insurer to handle expenses. Only the remaining amount (sometimes referred to as the allocated premium) is credited to the account. In the so-called unit linked policies popular in the United Kingdom, it is common to incorporate this expense by a device termed a bid–offer spread. In these cases the policyholder is deemed to have their own separate fund, distinct from the general assets of the company, and the premium is used to buy a number of units of the fund. These are bought at a certain offer price, and sold back at a lower bid price. So for example if the offer price was 100 per unit and the bid price was 95 per unit, and a premium of 1000 was paid, the purchaser would own 10 units of the fund, which would have a value of 950. So the allocated premium would be effectively 950.
3. e_k, an additional flat amount that is charged each period for expenses.
4. c_k, the cost of insurance rate. This is just a mortality rate which will apply to the time period running from time k to time k + 1. For a yearly calculation with an issue age of x, we would have c_k = q_{x + k}, for an appropriate life table. For a monthly calculation, assuming UDD, we would have c_k = (1/12)q_{x + m}, where 12m ≤ k < 12(m + 1). It is often expressed as a rate of so much per 1000. So for example a cost of insurance rate of 15 per 1000 would mean that c_k = 0.015.
5. i_k, the credited interest rate. This may be specified directly or tied to the performance of some other investments.
6. b_k, the death benefit paid at time k + 1 for death between time k and k + 1.

Then the recursion is just

(13.1)

For type A policies we have η_k = b_k − AV_{k + 1}, if this is positive, and we solve the equation for AV_{k + 1}. For type B policies where the death benefit is paid in addition to the face amount, η_k = b_k. Another possible type of arrangement is where the fund itself is returned at death, subject to a guaranteed minimum amount b_k. (As mentioned above, this may be ruled out in certain jurisdictions by taxation requirements.) In such case if AV_{k + 1} ⩾ b_k, we would have η_k = 0, while if AV_{k + 1} < b_k, we would have η_k = b_k − AV_{k + 1}.

It must be kept in mind that the account on a universal life policy should be viewed as belonging strictly to the particular policyholder, so while the account value is similar in nature to a retrospective reserve, it is not quite the same. For example, withdrawal rates and surrender values are not taken into account in this calculation as was done in some Chapter 12 formulas. To do so would mean that policyholder accounts would be augmented with positive gains from surrender, but these belong strictly to the insurer (as of course do surrender losses, should they arise).

Example 13.1 A universal life policy has a stated death benefit of 100 000, monthly premiums of 5000, monthly expenses of 100, and a further monthly expense charge of 4% of each premium. The annual credited interest rate is 8%, and the monthly cost of insurance rate in the 5th year of the policy is 30 per thousand. If the account value at the end of the 52nd month is 50 000, find the account value at the end of the 53rd month, assuming that the policy is (a) type B and (b) type A.

Solution. We first must calculate the applicable monthly interest rate which is (1.08)^1/12 − 1 = .00643. Then

1. AV₅₃ = (50 000 + 5000(0.96) − 100)(1.00643) − 0.03(100 000) = 52 051.72.
2. The 100 000 above is replaced with 100 000 − AV₅₃, and solving the equation we just obtain the Type B amount divided by (1 − 0.03).
   

Another calculation that will normally be done each period is to compute the cost of insurance (as opposed to the cost of insurance rate). This is sometimes abbreviated as COI_k, for the period running from time k to k + 1. (Some authors prefer a different indexing method and would refer to this as COI_{k + 1}. We prefer to have the index correspond to that of the cost of insurance rate c_k.) This is normally determined as at the beginning of each period, so if there are not sufficient funds to pay it, the policy would lapse in the absence of any guarantees to the contrary. In effect it can be viewed as the net single premium paid each period for the death benefit coverage. That is

So in the above example we would have

• COI₅₂ = (1.00643)^{− 1}(0.03)100 000 = 2980.83, for the type B policy and
• COI₅₂ = (1.00643)^{− 1}(0.03)(100 000 − 53 661.57) = 1381.27, for the type A policy.

There are some variations which can arise. In some circumstances the insurer may use a discount rate j_k in calculating the cost of insurance which is different from the credited interest rate i_k. In this case formula (13.1) would be modified to

(13.2)

which shows directly the insurance costs being deducted at the start of the period. Clearly when j_k = i_k, the interest factors cancel and we just get back the same formula as before. Notice however that in general we still have the same formula as before if we adjust the c_k. We change this to a new cost of insurance rate given by

The following illustrates.

Example 13.2 Redo Example 13.1 and calculate the cost of insurance, under the assumption of a 3% discount rate for the cost of insurance.

Solution. We can do all calculations by changing c_k from 0.03 to c′_k = 0.03(1.08)^1/12/(1.03)^1/12 = 0.03012. In the type B policy, this will change the value of AV₅₃ to 52 039.72 and COI₅₂ to (1.00643)^{− 1}(0.03012)100 000 = 2992.76. In the type A policy, this will change the value of AV₅₃ to 52 039/(1 − 0.03012) = 53655.83 and COI₅₂ to (1.00643)^{− 1}(0.00301)(100 000 − 53 655.83) = 1386.96.

Another modification may be necessary because of the corridor requirement. In a close situation, we must test whether an account value is sufficiently low to meet this restriction. Let cor_k denote the minimum allowable ratio of b_k/AV_{k + 1}. If AV_{k + 1}cor_k > b_k, we must redo the calculations. The death benefit will now be cor_kF_{k + 1} and η_k = (cor_k − 1)AV_{k + 1}.

Example 13.3 For the policies of Example 13.1, find AV₅₃ and COI₅₂ assuming that cor₅₃ = 1.9.

Solution. For the type B policy the corridor requirement is clearly satisfied and the answer will remain as calculated above.

For the type A policy, we check the original answer to see that 53 661.57(1.9) = 101 957 which is above 100 000, so we must recalculate:

and solving we get AV₅₃ = 53 604.40. The death benefit will increase to 101 848.36

13.3.1 DB plans

The usual type of DB plan provides that an employee will receive a life annuity, beginning at a specified normal retirement age, with a periodic payment K. Rules for calculating K are specified at the outset. It will normally depend on the employee’s salary and years of service. The type of annuity is often a whole life annuity, although there may be options to elect a guaranteed period, or a joint-life annuity with another individual, such a spouse. The income of course will be adjusted according to the nature of the annuity selected.

A typical formula is that K will be equal to r times the average of the employee’s last h years of salary times the number of years of service, for some specified r and h. As an example, suppose that the normal retirement age is 65, r = 0.02, h = 3 and that K is an annual payment. Consider an employee who is hired at age 30, retires at age 65, and whose last 3 years of salary were 89 000, 93 000, 100 000. The employee would then receive an annual pension of 0.02 × 35 × 94 000 = 65 800.

A measure which is used to compare various plans is known as the replacement ratio and it is simply the ratio of the pension to the final year’s salary. In the above example the replacement ratio would be 65.8%.

The quantity h will often be between 3 and 5 years. A possible variation involves plans, known as career average earnings plan where h is not fixed, but is equal to the complete number of years of service for each employee.

To evaluate benefits on such a plan the actuary will use an investment discount function v and a multiple-decrement table which will typically show decrements of disability, withdrawal from service, death and retirement. An additional necessary tool is a so-called salary scale S_x defined as follows. For some minimal age x₀, we have and then for y > x₀.

The scale is then used to estimate future salaries. For example, if an employee is earning an annual salary of J at age x, then an estimate of their annual salary as age x + h will be JS_{x + h}/S_x.

Pension plans must specify what benefits if any will be paid to those who leave the employee group for reasons other than retirement at the normal retirement age. Such reasons include disability, death, withdrawal from company employment and retirement at an age other than the normal one. We focus now on early retirement. Plans may specify that a person may receive pension benefits if they retire early, with some minimum criteria specified, which can depend on age and duration of employment. Early retirement means of course that the pension is paid for a longer period, and also that contributions into the plan will not be made for the remaining time to the normal date, so typically the pension income will be appropriately reduced. Rather than calculate the applicable amount of reduction in each case, it is usual to work out approximate figures, known as actuarial reduction factors and these are specified as part of the provisions of the plan.

In the following simplified example, provision is made for early retirement up to 2 years before the normal date, but not for other forms of decrement.

Example 13.4 Consider a DB plan which provides a yearly pension of 2% of the final 3-year average salary, times the number of years of service, for retirement at ages 63–65, but with a reduction of 5% per year should retirement occur before 65. An employee now 45 was hired at age 35. His/her present salary is 70 000. The salary scale is given by S_x = 1.03^{x − 30}, x ⩾ 30. (This simply means that salaries are expected to increase by 3% per year.) An employee may retire at any age from 63 to 65, with a reduction in pension income of 5% per year. Find a formula for the actuarial present value of the pension benefits.

Solution. For a person retiring at age 63, the estimated 3-year final average salary is given by

so that the estimated annual pension income, accounting for the actuarial reduction factor of 10%, is given by 0.90 × 0.02 × 28 × 112 262 = 56 630.

For person retiring at age 64 a similar calculation, now using a 5% reduction results in annual pension income of 63 769, and for a person retiring at age 65, the figure is 71 523.

The actuarial present value is then given by the following (the subscript r denoting the retirement decrement).

Our solution here incorporates several simplifying assumptions. We have assumed that the pension would be paid annually, instead of the more usual monthly arrangement. We have also assumed that all employees are hired and retired on their birthdays, and that each salary increase occurs on birthdays. It is not too difficult to incorporate more realistic assumptions, using the fractional duration techniques in Chapter 7. One common provision is to assume hiring, retirements, and salary increases at the middle of each year, that is at ages x + 1/2, where x is an integer.

Funds to provide the income could be provided solely by the employer, or more commonly shared between the employees and the employer on some specified basis. A usual provision is that the employees will contribute each period a amount of c times their salary for that period. A typical figure might be c = 0.05. The employer will then contribute additional amounts which are estimated to be sufficient to provide the promised benefits. There are various methods for doing so. The subject of funding DB pensions is complex, and will not be discussed further.

13.3.2 DC plans

At one time the DB arrangement was the most common one. However periods of low interest rate earnings and improving mortality meant that many employers needed to put in more money then originally estimated in order to ensure the promised level of benefits. In some cases this became prohibitive, resulting in firms switching to the DC mode. In such a pension, the employees contribute a certain percentage of their salary, the employer adds an additional percentage, and the funds are invested and accumulated as an individual account for each participant until retirement. At the time of retirement the total accumulated contributions made on the employee’s behalf are used to purchase an annuity at the then prevailing interest and mortality rates. As with the DB plan there is often a targeted goal, but this is not guaranteed. If the investment experience is unfavourable, or mortality has improved so that the cost of life annuities go up, the pension income may be short of the projected amount. Of course, things can go the other way in a DC plan. Very favourable investment returns can result in higher pensions than expected.

Funding arrangements are usually much easier for the DC plan than in the DB case. A common practice is to deposit into the account a certain fraction c of a employee’s salary each year, which could be shared in some way between the employee and employer. One does not have to worry as much about benefits for withdrawal or early retirement. Withdrawing employees can be given the amount in their account, either in cash or as a deferred annuity. For those retiring early the amount can be used to buy an annuity starting on the normal retirement date.

In the following examples, we continue to make the simplifying assumptions noted above,

Example 13.5 For an employee hired at age 35 at a salary of 50 000, it is estimated that an amount of 500 000 is needed at at the normal retirement age of 65 to buy an appropriate pension. For exit from the plan before age 65 the accumulated amount of contributions with interest is returned to the employee. Find a formula to calculate the contribution rate c, assumed to be made at the beginning of each year.

Solution. The idea is similar to Example 5.8. We solve the following equation to determine c.

(13.3)

where

(13.4)

There are many variations in practice. Many plans have a so-called vesting requirement, which means that an employee does not receive back the employer’s contributions unless they remain in the plan for a minimum period.

Example 13.6 Suppose that in the situation described above, the contributions are split, with the employee paying 40% and the employer the remaining 60%. For participants exiting the plan after 5 years, the total of all contributions with interest is returned at the end of the year of leaving. For those exiting in the first 5 years only the employee’s own contributions with interest are returned. Find an equation to determine the contribution rate c.

Solution. We use a variation of formula (5.5).

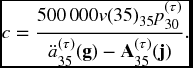
where g is as in (13.4) and