2

NUMBER SYSTEMS AND COMPUTER CODES

2.1 INTRODUCTION

Since the early days of human civilisation, people have been using their fingers, sticks, and other things for counting. It all started perhaps, with the need to figure out the assets a person had. As daily activities became more complex, numbers became more important in trade, time, distance, and in all other spheres of human life. It became apparent that we needed more than our fingers and toes to keep track of the number in our daily routine. Furthermore, ever since people discovered that it was necessary to count objects, they have been looking for easier ways of counting. To count large numbers, man soon started to count in groups, and various number systems were formed. This chapter discusses different types of number systems, conversion from one number system to another, and performing binary arithmetic operations. In addition, it also discusses various coding schemes to represent characters and numbers.

2.2 NUMBER SYSTEM

A number system defines a set of values used to represent ‘quantity’. Generally, one talks about a number of people attending class, or a number of modules taken by each student, and use numbers to represent grades achieved by students in tests. Quantifying values and items in relation to each other is helpful for us to make sense of our environment. The number system can be categorised into two broad categories:

• Non-Positional Number Systems: In ancient times, people used to count with their fingers. When fingers became insufficient for counting, stones and pebbles were used to indicate the values. This method of counting is called the non-positional number system. It was very difficult to perform arithmetic operations with such a number system, as it had no symbol for zero. The most common non-positional number system is the Roman number system. These systems are often clumsy and it is very difficult to do calculations for large numbers.
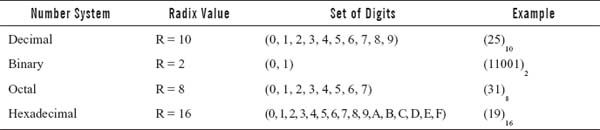
• Positional Number Systems: A positional number system is any system that requires a finite number of symbols/digits of the system to represent arbitrarily large numbers. When using these systems the execution of numerical calculations becomes simplified, because a finite set of digits are used. The value of each digit in a number is defined not only by the symbol, but also by the symbol's position. The most widely used positional number system is the decimal number system. With the emergence of the computer, other positional number systems like binary number system, octal number system, and hexadecimal number system also came in use.

Base (or Radix) of System

The word base (or radix) means the quantity of admissible marks used in a given number system. The admissible marks are the characters such as Arabic numerals, Latin letters, or other recognisable marks, which are used to present the numerical magnitude of a ‘quantity’. The decimal number system originated in India. This system has 10 as base of a number system and is indicated by a subscript (decimal number) and this is followed by value of the number. For example, (7592)₁₀ represents base 10 number system and (214)₈ represents base 8 number system.

For a computer, everything is in the digital form (binary form) whether it is number, alphabet, punctuation mark, instruction, etc. Let us illustrate with the help of an example. Consider the word ‘INDIA’ that appears on the computer screen as a series of alphabetic characters. However, for the computer, it is a combination of numbers. To the computer it appears as:

2.2.1 TYPES OF NUMBER SYSTEMS

Eventually, the number systems that are generally used by the computers are listed in Table 2.1.

Table 2.1 Types of Number Systems

The important thing about the number systems is that each system is just a different method for representing the quantities. Moreover, the quantities do not change but the symbols used to represent those quantities are changed in each number system.

Decimal Number System

The primary number system used is a base ten number system or decimal number system. The decimal system is the system which we use everyday while counting. The name is derived from the Latin word Decem, which means ten. This number system includes the ten digits from 0 through 9. These digits are recognised as the symbols of the decimal system. Each digit in a base ten number represents units ten times the units of the digit to its right.

Starting at the decimal point and moving to the left, each position is represented by the base (radix) value (10 for decimal) raised to a power. The power starts at 0 for the position just to the left of the decimal point. The power is incremented for each position that continues to the left.

Moving to the right of the decimal point is just like moving to the left except that we will need to place a minus sign in front of each power.

.10^-1 10^-2 10^-3

Consider the number 9735. In the first column of the following table, we write 9735 in the expanded notation. In the second column we write the same sum but express 9000 as 9 × 1000, 700 as 7 × 100, 30 as 3 × 10, and 5 as 5 × 1. In the third column, again we write the same numbers, but express 1000, 100, 10 and 1 as powers of 10.

Binary Number System

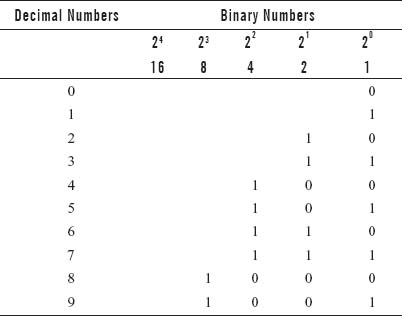
The digital computer provides accurate solutions to the problems by performing arithmetic computations. These numbers are not expressed as decimal numbers within the computer because it is not suitable for machine processes. Computers are not only powered by electricity, they compute with electricity. They shift voltage pulses around internally. When numbers are represented in a computer's memory by means of small electrical circuits, a number system with only two symbols is used. These symbols are ON or OFF states of the circuit. This system of representing numbers is known as the binary number system. Circuits allow electricity to flow or to be blocked depending on the type of circuit. Computer circuit is made out of transistors, which have only two states, ON and OFF. ON is interpreted as 1, while OFF as 0. Similar to the decimal system, the position of a digit in a number indicates its value. Instead of ones, tens, hundreds, thousands, etc., as in the decimal system, the columns in the binary system contains ones, twos, fours, eights, etc. Each additional column to the left has powers of 2, specifically, each place in the number represents two times (2×'s) the place to its right. Table 2.2 represents the first 10 binary numbers.

Table 2.2 Representing Decimal Numbers in Binary

Octal Number System

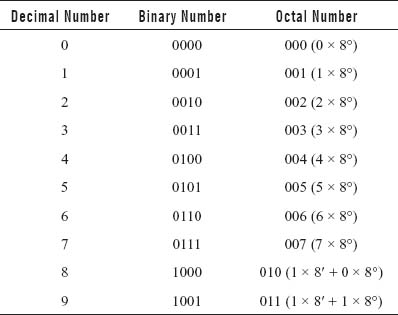
The octal number system is a base 8 system, having eight admissible marks: 0, 1, 2, 3, 4, 5, 6, and 7 with no 8's or 9's in the system. This system is a positional number system. The octal system uses powers of 8 to determine the digit of a number's position.

Table 2.3 Representing Binary and Decimal in Octal

Hexadecimal Number System

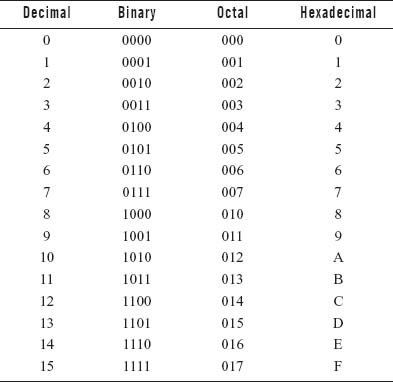
Hexadecimal system is similar to the decimal, binary, and octal number systems, except that the base is 16. Each hexadecimal number represents a power of 16. To represent the decimal numbers, this system uses 0 to 9 numbers and A to F characters to represent 10 to 15, respectively. The largest hexadecimal digit F is equivalent to binary 1111.

Table 2.4 Comparing Decimal, Binary, Octal, and Hexadecimal

2.2.2 CONVERSION BETWEEN NUMBER BASES

Computers and other digital systems process information as their primary function. Therefore, it is necessary to have methods and systems for representing information in forms, which can be manipulated and stored using electronic or other types of software. As discussed earlier, internally computer uses binary numbers for data representation whereas externally it uses decimal numbers. However, any number in one number system can be represented in another number system. Various methods, which can be used to convert numbers from one base to another are discussed in the following sections.

Converting Decimal to Binary, Octal, and Hexadecimal

The method used for the conversion of decimal number into other number systems is often done using the ‘remainder’ method. This method involves the following steps:

1. Divide the decimal number by the base of the target number system. That is, to convert decimal to binary, divide the decimal number with 2 (the base of binary number system), 8 for octal, and 16 for hexadecimal.
2. Note the remainder separately as the first digit from the right. In case of hexadecimal, if the remainder exceeds 9, convert the remainder into equivalent hexadecimal form. For example, if the remainder is 10 then note the remainder as A.
3. Continually repeat the process of dividing until the quotient is zero and keep writing the remainders after each step of division.
4. Finally, when no more division can occur, write down the remainders in reverse order.

Example 1: Determine the binary equivalent of (36)₁₀.

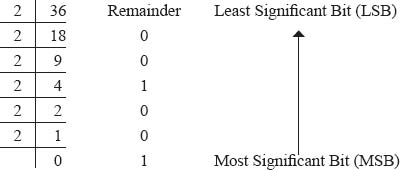
Taking remainders in reverse order, we have 100100. Thus, the binary equivalent of (36)₁₀ is (100100)₂.

Example 2: Determine the octal equivalent of (359)₁₀.

Thus, the octal equivalent of (359)₁₀ is (547)₈.

Example 3: Determine the hexadecimal equivalent of (5112)₁₀.

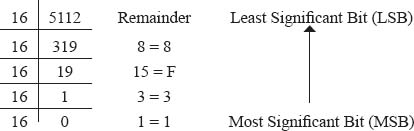
Thus, the hexadecimal equivalent of (5112)₁₀ is (13F8)₁₆.

Converting Binary, Octal, and Hexadecimal to Decimal

The method used for conversion of a binary, octal, or hexadecimal number to decimal number involves each digit of the binary, octal, or hexadecimal number to be multiplied by its weighted position, and then each of the weighted values is added together to get the decimal number.

Example 1: Determine the decimal equivalent of (11010)₂.

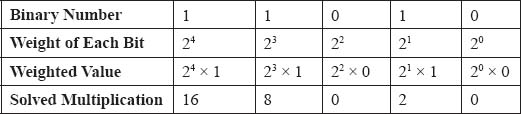
Sum of weight of all bits = 16 + 8 + 0 + 2 + 0 = 26

Thus, the decimal equivalent of (11010)₂ is (26)₁₀.

Example 2: Determine the decimal equivalent of (456)₈.

Sum of weight of all bits = 256 + 40 +6 = 302

Thus, the decimal equivalent of (456)₈ is (302)₁₀.

Example 3: Determine the decimal equivalent of (B14)₁₆.

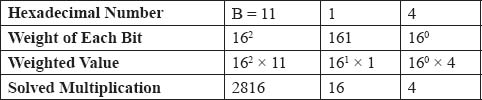
Sum of weight of all bits = 2816 + 16 + 4 = 2836

Thus, the decimal equivalent of (B14)₁₆ is (2836)₁₀.

Converting among Binary, Octal, and Hexadecimal

Converting among binary, octal, and hexadecimal can be accomplished easily without converting to decimal first, as the base numbers of all three systems (2, 8, and 16) are powers of 2. Any octal digit can be written as a group of three binary digits while a hexadecimal number will comprise four binary digits.

Example 1: Determine the octal equivalent of (010111)_2.

The octal equivalent of (010111)₂ is (27)₈.

Example 2: Determine the hexadecimal equivalent of (11001011)₂.

The hexadecimal equivalent of (11001011)₂ is (CB)₁₆.

Example 3: Determine the binary equivalent of (231)₈.

Thus, the binary equivalent of (231)₈ is (010011001)₂.

Example 4: Determine the binary equivalent of (5AF)₁₆.

Thus, the binary equivalent of (5AF)₁₆ is (010110101111)₂.

Converting between Octal and Hexadecimal

The method used for the conversion of octal number to hexadecimal number is accomplished by the following steps:

1. Convert each octal digit to 3-bit binary form.
2. Combine all the 3-bit binary numbers.
3. Segregate the binary numbers into the 4-bit binary form by starting the first number from the right bit (LSB) towards the number on the left bit (MSB).
4. Finally, convert these 4-bit blocks into their respective hexadecimal symbols.

Example 1: Determine the hexadecimal equivalent of (2327)₈.

Combining the 3-bit binary blocks, we have 010011010111. Separating the group of binary numbers (from left side) into the 4-bit binary number and by converting these blocks into their respective hexadecimal symbols, we have:

Thus, the hexadecimal equivalent of (2327)₈ is (4D7)₁₆.

The method used for the conversion of hexadecimal number to octal number is the same as the octal to hexadecimal conversion except that each hexadecimal digit is converted into 4-bit binary form and then after grouping of all the 4-bit binary blocks, it is converted into the 3-bit binary form. Finally, these 3-bit binary forms are converted into octal symbols.

Example 2: Determine the octal equivalent of (2B6)₁₆.

Combining all the 4-bit binary blocks, we have 001010110110. Separating the group of binary numbers into the 3-bit binary blocks and by converting these blocks into octal symbols, we have:

Thus, the octal equivalent of (2B6)₁₆ is (1266)₈.

2.3 COMPUTER ARITHMETIC

Arithmetic is a branch of mathematics that involves combining numbers by addition, subtraction, multiplication, and division. During school days, arithmetic was restricted only to decimal number system. However, in computer, we require arithmetic on other number systems such as binary, octal, and hexadecimal. In the following few sections, we will discuss how to perform basic arithmetic on these number systems.

2.3.1 BINARY ARITHMETIC

Everything that is stored in or manipulated by the computer is a number. The computer only understands the numbers 1 and 0. Therefore, every number has to be converted to binary (0s and 1s) digits. The basic arithmetic operations of the binary number system are addition and subtraction.

Binary Addition

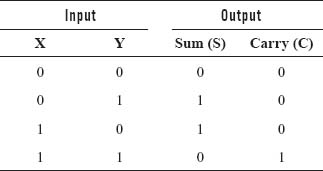
Binary addition is carried out in the same way as the decimal addition is performed. In decimal addition, the unit column is added first, then the tens column, the hundreds, and so on. If the sum is greater than or equal to ten, the least significant digit is written as a partial sum and a carry of 1 is added to the sum of the next column. This process is repeated for each larger significant digit. These steps are also followed in the binary addition. The addition table of the binary arithmetic is very simple because this system has only two digits. As a result, there are only four outcomes or rules of the binary addition as listed in Table 2.5.

Table 2.5 Addition of Binary Numbers

In the table above, the results of the four addition operations between the two binary digits are divided between the ‘sum’ and the ‘carry’ part. The first three outcomes are the simple arithmetic operations but in the fourth operation, a ‘carry-over’ condition occurs. This has been performed in the same manner as in decimal arithmetic according to which 1 is carried to the next higher column. However, since 1 is the largest possible digit in the binary system, any value which will be greater than 1 requires the digit to be carried over.

For instance, 10 plus 10 in the binary system requires addition of two 1s in the second position. Here, 1 + 1 = 0 plus a carry of 1. Hence, in the binary addition the sum of 10 + 10 is 100.

Example 1: Add the binary numbers 1111 and 1010 and check the answer with the help of decimal addition.

According to the last step of the above binary addition, 1 + 1 + 1 = 10 + 1= 11 = 1 + carry of 1 into higher column.

Example 2: Calculate the sum of 110011, 10010, 1100 and 101 and check the answer with the help of decimal addition.

Example 3: Add the binary fractional numbers 11.10 and 10.10 and check the result with the help of decimal addition.

Binary Subtraction

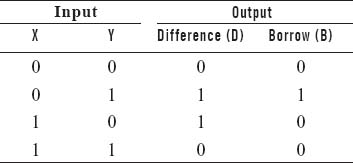
Subtraction is generally simple in comparison to addition since only two numbers are involved and the upper value representation is greater than the lower value representation. In binary subtraction, the problem of ‘borrow’ is similar to that in decimal. If the subtrahend bit is equal to or smaller than the minuend bit, then perform the subtraction, otherwise borrow one from its left most neighbour. If its neighbour is zero, then proceed to the left until a borrow can be performed. For the left most bit, a borrow is made from the outside.

We can construct a subtraction table (as shown in Table 2.6 below) that has two parts—the three cases of subtracting without borrow, and the one case of the involvement of a borrow digit, no matter how far to the left is the next available binary digit. Like the binary addition, binary subtraction also follows four rules for the operation. These rules are listed in Table 2.6.

Table 2.6 Subtraction of Binary Numbers

The rules, given in the above table, can be explained by the following example of subtraction.

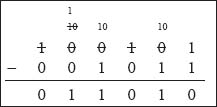
The following steps are involved:

1. First, for the least significant bit (the right most bit), 1 – 1 is 0.
2. For the next bit, 0 – 1 cannot be computed since the subtrahend is smaller than the minuend. Borrow 1 from the third bit to form the binary number 10 (decimal 2) and do the subtraction. The operation is 10 – 1 = 1 which in the decimal number system is 2 – 1 = 1.
3. For the third bit, since we borrowed 1 for the second bit, we have 0 – 0 that is 0.
4. For the fourth bit again, we cannot perform the subtraction. However, the fifth bit in the minuend is zero, so we must borrow from the sixth bit. This makes the fifth bit 10 (decimal 2). Borrowing 1 from the fifth bit makes it 1 and the fourth bit becomes 10 (decimal 2). Now the subtraction in binary is 10 – 1 = 1 which is the result of the fourth bit.
5. For the fifth bit, we now have 1 – 0 = 1.
6. Since we borrowed 1 from the sixth bit for the fourth bit, so for the sixth bit, the subtraction is 0 – 0 = 0.

Example 1: Find the binary difference of (1101–10110) and check the answer with the help of decimal subtraction.

Note: Here, we borrowed 1 from third column because of the difference 0–1 in the second column.

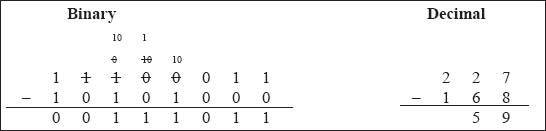
Example 2: Calculate the binary difference of (11100011–10101000) and check the answer with the help of decimal subtraction.

2.3.2 OCTAL ARITHMETIC

In the computer, everything that is stored in or manipulated is in a form of binary number. Nevertheless, the octal number system is also a common system, which has been used with the computers. The essential arithmetic operations of the octal number system are addition and subtraction.

Octal Addition

Addition of the octal number is carried out in the same way as the decimal addition is performed. The steps are given below:

1. First, add the two digits of the unit column of the octal number in decimal.
2. This process is repeated for each larger significant digit of the octal number.
3. During the process of addition, if the sum is less than or equal to 7, then it can be directly written as a octal digit.
4. If the sum is greater than 7, then subtract 8 from that particular digit and carry 1 to the next digit position.

Note: In this addition, we should remember that the largest octal digit is 7 instead of 9.

Example 1: Add the octal numbers 26 and 17.

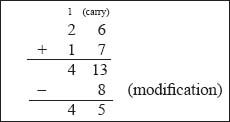
Thus, the resultant octal sum is 45.

Example 2: Add the octal numbers 5647 and 1425.

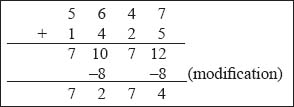
Thus, the resultant octal sum is 7274.

Octal Subtraction

In the octal subtraction, the method, which we have adopted, is similar to that of binary subtraction method. The only difference lies in the carry part. During octal subtraction, instead of 1, we will borrow 8 and the rest of the steps are similar to that of binary subtraction.

Example 1: Subtract (677)₈ from (770)₈.

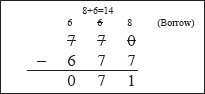
Thus, the difference is (71)₈.

Note: Here, we borrowed 8 from the second column for the difference 0–7 and 8 from the third column for the difference 6–7.

Example 2: Subtract (2761)₈ from (6357)₈.

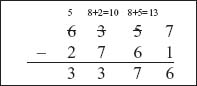
Thus, the difference is (3376)₈.

2.3.3 HEXADECIMAL ARITHMETIC

The hexadecimal number system is extensively used in the memories of the computer system and in the computer instructions. The basic arithmetic operations that are to be performed are addition and subtraction.

Hexadecimal Addition

The addition operation performed with the hexadecimal numbers is analogous to the decimal addition except with a few differences that are discussed in the following steps:

1. First add the unit column of the hexadecimal digits in decimal.
2. This process is repeated for each larger significant digit of the hexadecimal number.
3. During the process of addition, observe if the sum is 15 or less, then it can be directly expressed as a hexadecimal digit.
4. If the sum is greater than 15, then subtract 16 from that particular digit and carry 1 to the next digit position.

Example 1: Add the hexadecimal numbers (76)₁₆ and (45)₁₆.

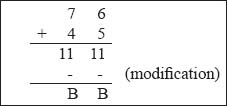
Thus, the hexadecimal sum is (BB)₁₆.

Note: In the above example, since the decimal sums are less than 15 so they are expressed directly in the hexadecimal form.

Example 2: Add the hexadecimal numbers (A27E9)₁₆ and (6FB43)₁₆.

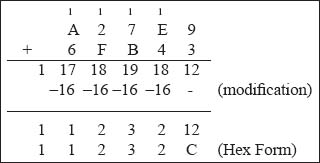
Thus, the hexadecimal sum is (11232C)₁₆.

Hexadecimal Subtraction

The hexadecimal subtraction is based on the same principles as that of binary subtraction. In this subtraction, 16 will be used as borrow instead of 1. The rest of the steps are similar to the binary subtraction.

Example 1: Subtract (75)₁₆ from (527)₁₆.

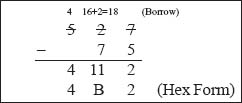
The hexadecimal difference is (4B2)₁₆.

Example 2: Subtract (1F65)₁₆ from (7E2CA)₁₆.

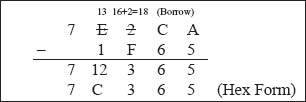
The hexadecimal difference is (7C365)₁₆.

2.4 CODING SCHEMES

In today's technology, the binary number system is used by the computer system to represent the data in the computer understandable format. Numeric data (consists of only numbers 0, 1, 2… 9) is not the only form of data, which is handled by the computer. Alphanumeric data (it is a string of symbols of the letters A, B, C… Z or the digits 0, 1, 2… 9) and some special characters such as =, –, +, *,/, (,), etc., are also required to be processed by the computer. There are lot of ways to represent numeric, alphabetic, and special characters in computer's internal storage area. In computers, the code is made up of fixed size groups of binary positions. Each binary position in a group is assigned a specific value; for example 8, 4, 2, or 1. In this way, every character can be represented by a combination of bits that is different from any other combination. Moreover, data can also be arranged in a way that's very simple and easy to decode, or transmitted with varying degrees of redundancy for error detection and correction. Although there are many coding schemes available for representing characters, some commonly used coding systems are Binary Coded Decimal (BCD), American Standard Code for Information Interchange (ASCII), and Extended Binary Coded Decimal Interchange Code (EBCDIC).

2.4.1 BCD

Binary Coded Decimal (BCD) is a method of using binary digits to represent the decimal digits 0 to 9. A decimal digit is represented by four binary digits. The BCD coding is the binary equivalent of the decimal digit. BCD system was developed by the IBM (International Business Machines) corporation. With BCD, each digit of a number is converted into its binary equivalent rather than converting the entire decimal number to its binary form. Similarly, letters and special characters can be coded in the binary form.

Let us determine the BCD value for the decimal number 5319. Since there are four digits in our decimal number, there are four bytes in our BCD number. They are:

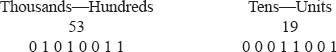
Binary code decimal digits (0–9) are represented using 4-bits. The valid combinations of bits and their respective values are shown in Table 2.7.

Table 2.7 Binary Coded Decimal

Decimal Code	BCD Digit
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001

One of the advantages of the BCD system is that there is no limit to the size of a number. For adding another digit, we just have to add a new 4-bit sequence. In contrast, numbers represented in binary format are generally limited to the largest number, which can be represented by 8, 16, 32 or 64 bits. Moreover, this is a fast way to convert numbers from decimal to binary. However, this coding is not sufficient for business purposes as it can represent only 16, that is, 2⁴ symbols.

The later version of BCD used a 6-bit code. These BCD codes defined six-bit words, which allowed representing a maximum of 64, that is, 2⁶ symbols. Computers using BCD codes could work only with upper case letters and 0 to 9 numbers and few characters. However, the modern computers do not use BCD numbers as they have to process names and other non-numeric data.

2.4.2 ASCII

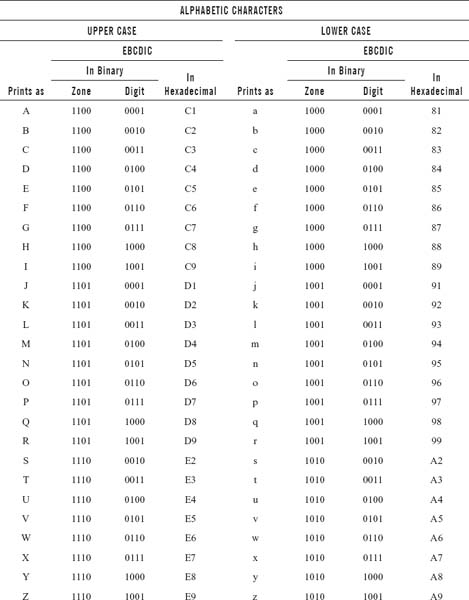
The standard binary code for the alphanumeric characters is ASCII. This code was originally designed as a 7-bit code. Several computer manufacturers cooperated to develop this code for transmitting and processing data. Later on, IBM developed a new version of ASCII, called as ASCII-8. They made use of all eight bits providing 256 symbols. Nevertheless, IBM had not changed the original set of 128 codes so that the original instructions and data could still work with the new character set. ASCII is commonly used in the transmission of data through data communication and is used almost exclusively to represent the data internally in the microcomputers. In ASCII, rather than breaking letters into three groups, upper case letters are assigned codes beginning with hexadecimal value 41 and continuing sequentially through hexadecimal value 5A. Similarly, lower case letters are assigned hexadecimal values of 61 through 7A.

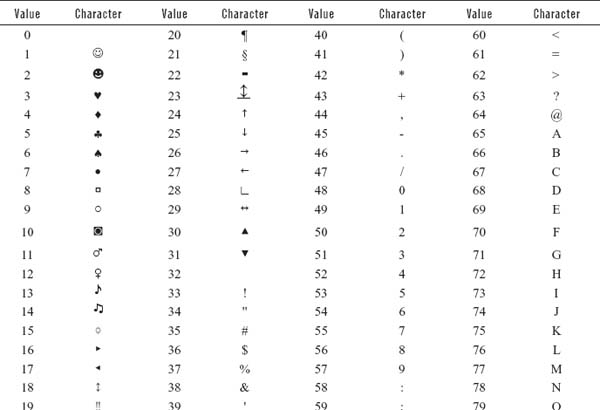
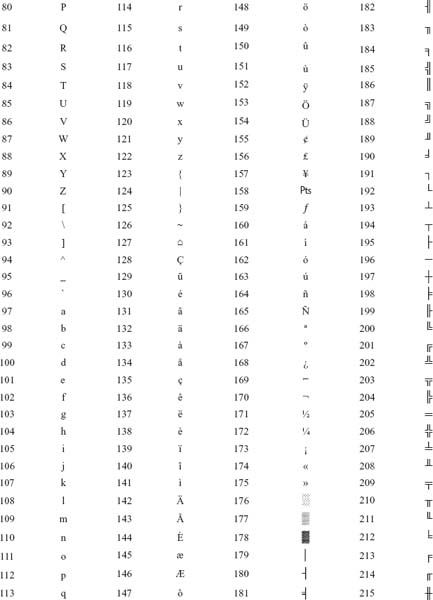
The decimal values 1 to 9 are assigned the zone code 0011 in ASCII. Table 2.8 of ASCII coding chart shows upper case and lower case alphabetic characters and numeric digits 0 to 9. The standard ASCII code defines 128 character codes (from 0 to 127), of which, the first 32 are control codes (non-printable), and the other 96 are representable characters.

Table 2.8 ASCII Coding Chart

Example: Determine the binary coding of ‘words’ in the ASCII form.

The corresponding ASCII codes for ‘words’ are:

2.4.3 EBCDIC

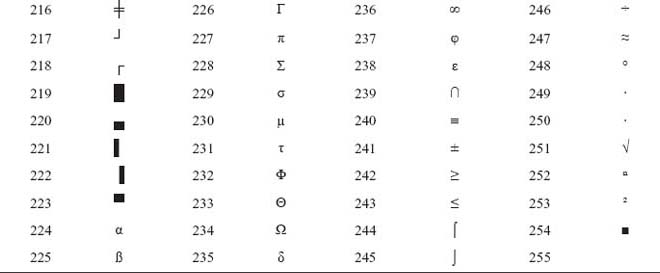
EBCDIC uses 8 bits for each character, it is possible to represent 256 different characters or bit combinations. This provides a unique code for each decimal value 0 to 9 (for a total of 10), each upper case and lower case letter (for a total of 52), and for a variety of special characters. Since it is an 8-bit code, each group of the eight bits makes up one alphabetic, numeric, or special character and is called a byte.

In EBCDIC, the bit pattern 1100 is the zone combination (zone and digit) used for the alphabetic characters A through I, 1101 is used for the characters J through R, and 1110 is the zone combination used for characters S through Z. The bit pattern 1111 is the zone combination used when representing decimal digits. For example, the code 1100 0001 is equivalent to the letter A; the code 1111 0001 is equivalent to the decimal digit 1. Other zone combinations are used when forming special characters. The concepts and advantages of ASCII are identical to those of EBCDIC. The important difference between the two coding systems lies in the 8-bit combinations assigned to represent the various alphabetic, numeric, and special characters. While using ASCII 8-bit code, we notice that the selection of bit patterns used in the positions differs from those used in EBCDIC. For example, let us look at the characters DP3 in both EBCDIC and ASCII to see how they compare.

Table 2.9 EBCDIC Codes

LET US SUMMARISE

1. A number system defines a set of values used to represent ‘quantity’. It can be categorised into two broad categories: non-positional and positional number systems.
2. In a non-positional number system, special symbols or characters are used to indicate the values. It is very difficult to perform arithmetic with such a number system, as it has no symbol for zero.
3. In a positional number system, the value of each digit in a number is defined not only by the symbol, but also by the symbol's position. The most popular positional number system being used today is the decimal number system.
4. The base or radix of the number system tells the number of symbols or digits used in the system. The base of the decimal number system is 10, of binary number system is 2, of octal number system is 8, and of hexadecimal number system is 16.
5. The number systems that are generally used by the computers are decimal number system, binary number system, octal number system, and hexadecimal number system.
6. The decimal number system includes the ten digits from 0 through 9. These digits are recognised as the symbols of the decimal system. Each digit in a base ten number represents units ten times the units of the digit to its right.
7. The binary number system is based on the number two and deals with only two numbers: 0 and 1.
8. The octal number system is a base 8 system, having eight admissible marks: 0, 1, 2, 3, 4, 5, 6, and 7 with no 8's or 9's in the system. It uses powers of 8 to determine the digit of a number's position.
9. Hexadecimal system is similar to the decimal, binary, and octal number systems, except that the base is 16. Each hexadecimal number represents a power of 16.
10. Any number in one number system can be represented in another number system such as decimal to binary, octal, and hexadecimal, etc.
11. The computers perform the arithmetic operations in the binary mode. The basic arithmetic operations that have been performed by all the number systems are addition and subtraction.
12. In computers, the coding scheme is made up of fixed size groups of binary positions, where each binary position in a group is assigned a specific value. Some of the commonly used coding systems are Binary Coded Decimal (BCD), American Standard Code for Information Interchange (ASCII), and EBCDIC.
13. Binary Coded Decimal (BCD) is a method of using binary digits to represent the decimal digits 0 to 9. A decimal digit is represented by four binary digits.
14. The standard binary code for the alphanumeric characters is ASCII. This code was originally designed as a 7-bit code. Several computer manufacturers cooperated to develop this code for transmitting and processing data. Later on, IBM developed a new version of ASCII, called as ASCII-8. They made use of all eight bits providing 256 symbols.

EXERCISES

Fill in the Blanks

1. The radix of hexadecimal number system is _________.
2. The _________ number system is the most widely used positional number system.
3. The _________ method is used to convert the decimal number into other number systems.
4. The decimal equivalent of (131)₈ is ___________.
5. The decimal values 1 to 9 are assigned the zone code _________ in ASCII.
6. In BCD, one decimal digit is represented by ________ bits.
7. The ASCII code stands for __________.
8. The result of (11.110)₂ + (1101.001)₂ is _________.
9. The word decimal is derived from the Latin word ________, which means _________.
10. In positional number systems, the value of each digit is indicated by its __________ in the number.

Multiple Choice Questions

1. Roman number system is a
   • (a) Positional number system
   • (b) Non-positional number system
   • (c) Both (a) and (b)
   • (d) None of these
2. The number system on which the modern computers operate is
   • (a) Decimal number system (b) Octal number system
   • (c) Binary number system
   • (d) Hexadecimal number system
3. The binary equivalent of (231)₁₀ is
   • (a) 11100111
   • (b) 10111001
   • (c) 01110011
   • (d) None of these
4. The binary coding system that represents 256 different characters or bit combination is
   • (a) BCD
   • (b) ASCII
   • (c) Both (a) and (b)
   • (d) EBCDIC
5. The binary values that are formed when two bits are used are
   • (a) 00 and 10
   • (b) 11 and 00
   • (c) 00, 01, 10, and 11
   • (d) None of these
6. The octal addition of (25)₈ and (15)₈ is
   • (a) (42)₈
   • (b) (40)₈
   • (c) (41)₈
   • (d) None of these
7. The hexadecimal subtraction of (56)₁₆ from (427)₁₆ results in
   • (a) (3B1)₁₆
   • (b) (331)₁₆
   • (c) (371)₁₆
   • (d) (3D1)₁₆
8. The octal equivalent of (97)₁₀ is
   • (a) (97)₈
   • (b) (140)₈
   • (c) (41)₈
   • (d) (141)₈
9. Which of the following is the ASCII code for the text IF.
   • (a) 7370
   • (b) 7073
   • (c) 7271
   • (d) 7172
10. The number of admissible marks used in a given number system is known as
    • (a) Weight
    • (b) Base
    • (c) LSB
    • (d) MSB

State True or False

1. Any number in one number system can be represented in any other number system.
2. The octal system uses powers of 2 to determine the digit of a number's position.
3. A non-positional number system is any system that requires a finite number of symbols/digits of the system to represent arbitrarily large numbers.
4. Octal number system is a positional number system.
5. The largest hexadecimal digit F is equivalent to binary 1111.
6. There are four outcomes or rules of the binary addition.
7. The octal equivalent of number (972)₁₆ is (4652)₈.
8. The binary difference of 1101 and 1011 is 0110.
9. The number (10)₈ is a binary number.
10. The valid number that exists after (27)₈ is (30)₈.

Descriptive Questions

1. What is number system? Write the difference between positional and non-positional number system.
2. Perform the following conversions:
   • (a) (00011011)₂ = (?)₁₀
   • (b) (278)₁₀ = (?)₂
   • (c) (19B116)₁₆ = (?)₂
   • (d) (7623)₈ = (?)₁₆
   • (e) (5DA2)₁₆ = (?)₈
   • (f) (1476)₈ = (?)₂
3. Perform the following arithmetic operations:
   • (a) (1010)₂ + (1101)₂
   • (b) (101.11)₂ + (11.001)₂
   • (c) (1000011)₂ – (00110101)₂
   • (d) (A7.2B5)₁₆ + (4D.569)₁₆
   • (e) (7253.35)₈ – (3425.12)₈
   • (f) (00001010)₂ – (00110011)₂
4. Write down the steps involved in the method used for converting octal numbers to hexadecimal numbers.
5. Explain how a decimal number is converted into binary, octal, and hexadecimal number and vice versa. Give an example of each conversion.
6. Give the reasons as to why the binary number system is utilised for modern electronic digital computers.
7. What is the purpose of coding schemes? Explain different coding schemes in brief.
8. Describe the procedure used to add two hexadecimal numbers. Explain with the help of an example.

ANSWERS

Fill in the Blanks

1. 16
2. Decimal
3. Remainder
4. 89
5. 0011
6. Four
7. American Standard Code for Information Interchange
8. 10000.111
9. Decem, ten
10. Position

Multiple Choice Questions

1. (b)
2. (c)
3. (a)
4. (d)
5. (c)
6. (a)
7. (d)
8. (d)
9. (a)
10. (b)

State True or False

1. True
2. False
3. False
4. True
5. True
6. True
7. False
8. True
9. False
10. True