Introduction
Generic Algorithms
Abstract mathematical structures usually have a large number of models. Algorithms based on operations and laws of such structures therefore have an identical form: they are generic. This means that for each particular instance of the structure, only the basic operations have to be adapted, whereas the overall algorithm remains the same. The simplest and typical problem is the one of sorting. It applies to totally ordered structures with an order relation ≤. Any sorting algorithm can be formulated in terms of the order relation ≤ and it can be adapted to any particular model of an order relation by specifying this relation; for example for integers, real numbers or for a lexicographical order relation of alphanumeric strings. In addition, many programming languages allow for generic programming, i.e. in their syntax they provide the means to formulate generic algorithms and to specialize them to particular instances. In this book, an abstract algebraic structure called valuation algebra is proposed. It provides the foundation to formulate an abstract inference problem, to construct a graphical data structure and a generic inference algorithm to solve the inference problem. Usually, one arrives at such general structures from concrete problems and algorithms by lifting them to their most abstract form. This also holds for the present case. In 1988, Lauritzen and Spiegelhalter (Lauritzen & Spiegelhalter, 1988) proposed an algorithm for solving the inference problem for Bayesian networks based on a paradigm called local computation. Soon after, Shenoy and Shafer (Shafer & Shenoy, 1988; Shenoy & Shafer, 1990) noted that the same algorithm could also be applied to solve inference problems with belief functions. They proposed a small but sufficient system of axioms for an algebraic framework that makes possible the application of the generic inference algorithm. The algebraic theory of valuation algebras was developed in (Kohlas, 2003), and it was shown that they permit, under certain varying additional conditions, four different generic inference architectures. In (Pouly, 2008) a computer implementation of these generic architectures together with a number of concrete instances is described, see also (Pouly, 2010).
In the meantime, many different models of valuation algebras from very distant fields of Mathematics and Computer Science were identified. They range from probabilistic and statistical systems, different uncertainty formalisms to constraint systems, passing by various systems of logic, relational databases and systems of linear equations over fields and semirings. Many of these instances are presented in this book. Their computational interest can always be expressed in terms of the general inference problem, which can be solved by the same generic algorithm or inference architectures. This is first and foremost of great practical interest. Instead of developing and programming inference algorithms for each instance separately, it is possible to use a single generic system. Of course, in the past, individual solution algorithms and computer programs have been proposed and written mostly independent from each other, using the same basic concepts but often naming them quite differently. This adds to a certain Babylonian confusion, especially for students who should get an overall view of Computer Science. Further, it also represents a dissipation of valuable human resources in research and problem solving.
Second, the process of abstraction is of great theoretical importance. It provides a unifying view of seemingly different fields of Computer Science and allows to elaborate both similarities and differences between problem classes. In fact, valuation algebras allow for a very appealing general view of information processing: information comes in pieces, usually from different sources. Each piece of information concerns a particular domain and answers, possibly only partially, specific questions. Pieces of information can be aggregated or combined, which is one of the basic operations of a valuation algebra. So, the general inference problem essentially consists of combining all available information. But usually one is only interested in some particular facet or aspect of the total information. Therefore, the parts of the total information, which are relevant to precise questions, must be extracted. Extraction or projection of information is the second basic operation of a valuation algebra. In relational databases for example, combination corresponds to the join operation, whereas information extraction corresponds to the usual operation of projection in the relational algebra. So, valuation algebras show that this scheme of relational algebra is much more general. The form and nature of information elements may be very different from model to model.
Complexity Considerations
Combining pieces of information to solve the inference problem leads to what can be called a race of dimensionality. It was said above that each piece of information is associated with a certain domain. Combining information results in information on larger domains. So, when many pieces of information are combined, the domains may become very large. This often leads to serious problems of computational complexity, as we are next going to illustrate with two simple examples (Aji & McEliece, 2000):
Example I.1 Let f(X1, X2), g(X2, X3) and h (X2, X4, X5) be three real-valued functions, where X1 to X5 are variables taking values from a finite set of n elements. Such discrete functions can always be represented in tabular form. This leads to tables with n2 entries for f and g, and a table with n3 entries for the function h. If we identify combination with component-wise multiplication, and projection with the summation of unrequested variables, we may define the following inference problem:
Note that we combine all available information and project the result afterwards to the domain of interest, represented by the variable set {X1, X2}. This set is also called the query of the inference problem, whereas the set of factors f, g and h is called knowledgebase. Although each knowledgebase factor can be represented by a small table of at most n3 entries, the total product already needs a table of n5 entries. In our small example, this may still be tractable, but the reader will recognize that with growing numbers of factors and variables, computing this product will fast become intractable. In fact, if s denotes the total number of variables, the complete table over all variables has ns entries. We can see that this exhibits an exponential growth in the total number of variables. Thus, although the size of each factor in the knowledgebase may be small, computing their combination may be intractable. The next example points out a more realistic situation.
Example I.2 For 1 ≤ i ≤ 100 we consider 100 real-valued functions, where each function fi is defined over exactly three binary variables Xi to Xi+2. Again, each of these functions is representable by a table of 23 = 8 entries. Similarly to the foregoing example, we then choose the variable set {X101, X102} as query and obtain the following inference problem:
Here, each factor is represented by a small table of 23 entries. The total product on the other hand needs a table of 2102 entries that requires 1018 terabytes of memory. There is no computer with such a large memory capacity. If we further assume that a computer performs one multiplication per nanosecond, then these computations require at least 1012 years, which is 100 times longer than the estimated age of the universe. We therefore conclude that the above sum cannot be computed by first computing the total product and then summing out the hundred variables. This example is quite representative for the inference problems considered in this book.
So, what is then the escape from this race of dimensionality? We sketch the basic idea using the above examples. The secret lies in a clever use of the distributive law of arithmetics, which can often be used to arrange sequences of summations and multiplications such that all intermediate results stay manageable. This allows us to write equation (I.1) as
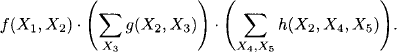
We immediately observe that the largest intermediate result produced during the computation of this formula contains 2 variables and thus requires a tables of only n2 entries. This is a considerable increase of efficiency which becomes even more apparent by applying the same idea to equation (I.2). We obtain
(I.3) 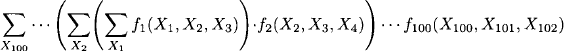
Here, the largest intermediate result contains only 3 variables that requires a table of 8 entries. Thus, instead of this huge amount of memory and computational time, the required resources remain proportional to the input size. Note also that besides the distributive law, we used the associative laws of addition and multiplication.
We may change the operation that is associated with projection in the above examples. Instead of addition, we now take the maximum value in Example I.1 that then leads to the following computational task:
Both expressions (I.1) and (I.4) model inference problems over different valuation algebras, whereas the second problem now takes the shape of an optimization task. Obviously, the same complexity considerations with respect to the size of intermediate tables apply in both cases, and because the distributive law still holds between multiplication and maximization, we may also perform the same improvement:
We thus have two different problems with different semantics and perhaps different application fields, but from the algebraic perspective they are both specializations of the same generic problem and can be solved by the same generic algorithm. This is exactly the idea of generic inference, and the secret of efficiency consists of a clever arrangement of the computations (combinations and projections) based on a generalization of the distributive law. Essentially the same technique was applied in the past for the processing of every specific inference formalism, which attests that the developers of these algorithms did not only solve the same generic problem, but they were also confronted with the same complexity concerns and finally hit upon the same solution. This is once more a convincing argument for the necessity of a generic inference theory, as it will be developed in the first part of this book.
The essence of valuation algebras consists in capturing these associative and distributive laws with respect to abstract operations of combination and projection. This will then be sufficient to rearrange the computations in the inference problem such that they remain feasible at each stage. In fact, this technique tends to keep storage proportional to the domain size of the input factors of the inference problem. One speaks of local computation, i.e. local on the domains of individual factors. Local computation is closely related to a well-known technique called tree-decomposition of graphs. Suppose a graphical representation of an inference problem where each node represents a variable. In addition, two nodes are linked by an edge, if their variables occur in the domain of a common factor or in the query. Figure I.1 shows the graph associated with the inference problem of Exercise I.1. If we again assume that there are s variables, each with a domain of n values, then the total information represented by the graph needs a table of ns entries.
Figure I.1 The graph associated with the inference problem of Exercise I.1.
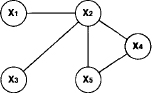
The key parameter, called treewidth ω of the graph, represents an important structural property. For the time being, we can imagine the treewidth as some measure related to the sparsity of the graph. Then, instead of the intractable complexity of ns associated with the total graph, the operations of the inference problem can be rearranged in such a way that the complexity is reduced to g(s) · nw, where g is a linear function. Observe that the complexity is still exponential, but now in the treewidth ω instead of the total number of variables s. Since in many cases ω is much smaller than s, it represents a big gain and often turns a intractable problem into a tractable problem. This is a case of what has recently been called parametric or parameterized complexity; see for example (Downey & Fellows, 1999). However, we should also emphasize that the complexity of inference problems is not always exponential. There are important cases where it may be polynomial, for instance s3 with s still being the number of variables. But we then still have the change in complexity from s3 to g(s) · ω3. It may thus be said that the polynomial or exponential complexity of the inference problem is a dimension somehow orthogonal to the framework of valuation algebras; but it always allows to reduce the complexity to a product of a linear function of problem size s and a polynomial or exponential function of treewidth ω according to the nature of the problem. That is essentially what valuation algebras achieve in terms of complexity.
Generic Constructions
From a practical point of view, the relevance of a generic theory can best be measured by the number of instances and applications covered by the theory. Here, a formalism is called an instance of a valuation algebra, if it satisfies the properties or axioms of the algebra. Besides the many concrete, individual instances presented in this book, we also describe generic approaches to construct whole classes of valuation algebras. We call this generic constructions. Essentially, these methods derive valuation algebras in a constructive manner from other algebraic structures such as fields, vector spaces or semirings. For example, we will see that matrices over particular semirings, systems of linear equation over arbitrary fields or mappings from configurations to semiring values always form a valuation algebra. Another generic construction identifies algebras derived from structures of languages with models, as in logic and many other fields. This adds to picture elements of valuation algebras as pieces of information, since information is often expressed in terms of a language; i.e. a formal language in our case. Generic constructions further allow to verify axioms and properties for whole classes of formalisms on a more abstract level and thereby simplify the theory. Finally, they also identify new formalisms that can be processed efficiently by the generic inference algorithms but which are yet unknown to the community.
The Content of this Book
This book is divided into three parts. The first part introduces the algebraic system of a valuation algebra and defines generic inference algorithms for their processing. The second part is entirely dedicated to generic constructions and the identification of new valuation algebra instances. Finally, the third part studies some selected applications of local computation. Some of these applications even go beyond the pure computation of inference, but they are nevertheless based on the same computational techniques. Typical examples are the construction of solutions for constraint and equation systems and sparse matrix techniques. Let us consider the organisation of the three parts in more detail:
Part I: Local Computation
Chapter 1 introduces the valuation algebra framework upon which all later chapters are based. For simplicity, we do not stress the most general axiomatic system that is based on arbitrary lattices with partial projection. Instead, we restrict ourselves to valuation algebras with full projection over variable systems that cover most practical applications. The two generalizations will be discussed in the appendix of this chapter. Also, we give first examples of well-known formalisms that satisfy the structure of a valuation algebra, including crisp constraints, relations, probability mass functions, belief functions or density functions.
Chapter 2 is dedicated to the definition of the generic inference problem that reflects the fundamental computational interest in valuation algebras. It will be distinguished between single-query and multi-query inference problems. We also introduce several possibilities to represent the structure of knowledgebases and give important applications that require the solution of inference problems with knowledgebases from different valuation algebras. This includes reasoning in Bayesian networks and Dempster-Shafer theory, satisfiability in logic and constraint systems, or discrete Fourier and Hadamard transforms.
Chapter 3 provides generic algorithms for the solution of single-query inference problems. In particular, it introduces the fusion algorithm, the bucket-elimination scheme and two variations of the collect algorithm. We also provide a detailed complexity analysis of these first local computation methods.
Chapter 4 extends the collect algorithm to take multiple queries into consideration, leading to the Shenoy-Shafer architecture. We will see that its complexity can be improved if the valuation algebra provides some concept of division. Based on this additional operator, three further local computation architectures for the solution of multi-query inference problems called Lauritzen-Spiegelhalter, Hugin and idempotent architecture are derived. The study of the algebraic requirements of a valuation algebra to provide a division operator is a more ambitious topic. Its comprehensive discussion is therefore postponed to the appendix of this chapter.
Part II: Generic Constructions
Chapter 5 presents the first generic construction that identifies valuation algebras by means of a simple mapping from configurations to values of a commutative semiring. This family of valuation algebras for example includes probability potentials, crisp constraints, weighted constraints, probabilistic constraints, possibilistic constraints and assumption-based constraints. A second family of valuation algebras is obtained from mapping sets of configurations to semiring values and includes in particular the formalism of belief functions from Dempster-Shafer theory.
Chapter 6 introduces path problems and shows that their computation amounts to the solution of a semiring fixpoint equation system. Based on this observation, two generic constructions related to matrices with semiring values are identified. Typical members and application fields of these families of valuation algebras are shortest path problems, maximum capacity problems, connectivity problems, path reliability, path counting, Markov chains or partial differentiation. Moreover, this chapter provides the preliminary work for the discussion of sparse matrix techniques in Chapter 9.
Chapter 7 deals with the duality between information and its representation in terms of a language. Typical examples of this generic construction are different kinds of logic and systems of equations and inequalities.
Part III: Applications
Chapter 8 points out that many valuation algebra have an associated notion of a solution. This is typically the case for systems of equations and inequalities, but it also holds in logic and constraint systems. The identification of solutions in arbitrary valuation algebras is the main topic in this chapter. It will be shown that based on a previous execution of a local computation architecture, solutions can be found without increasing the complexity of the local computation scheme. This results in two further generic algorithms to compute either a single solution or all solutions of a valuation given as factorization. In the second part of Chapter 8, this theory is applied to semiring constraint systems for the computation of solutions in optimization or constraints problems. Further specializations for equation systems will be discussed in Chapter 9.
Chapter 9 deals with sparse matrix techniques. The first part of the chapter focuses on sparse, linear systems over fields. It introduces Gaussian elimination and different decomposition approaches and establishes the connection to the valuation algebra of affine spaces introduced in Chapter 7. The famous least squares method provides an interesting case study. In the second part, we consider path problems that induce sparse fixpoint equation systems over semirings. This is based on the valuation algebras from Chapter 6. We will further show how local computation is used to solve the single-source, multiple-pairs or all-pairs version of different path problems.
Chapter 10 looks at linear systems with stochastic disturbances. In many important applications, these disturbances may be assumed to have a Gaussian distribution. Together with observations, such systems provide Gaussian information. It will be shown that several valuation algebras including Gaussian potentials and Gaussian hints hide behind Gaussian information. Also, this chapter investigates inference in Gaussian systems with local computation and provides an in-depth study of statistical, assumption-based reasoning.
All chapters in this book are completed by a collection of exercises and open problems. We distinguish three degrees of difficulty. One-star exercises are either simple finger exercises to actively digest the theory of the chapter, straightforward applications of the theory to concrete problems or omitted proofs with a reference to another textbook or journal article that contains the complete proof. Two-star exercises are small research projects that extend the theory of the chapter and establish links to related research topics. Finally, three-star exercises label comprehensive and mainly open research questions that could be included in a research program on valuation algebras and local computation.
Beyond the Content of this Book
This book is about generic local computation or tree-decomposition methods that are derived from the general valuation algebra framework. Additionally, we discuss several specializations and extensions of these algorithms for particular families of valuation algebras in the third part. However, it should also be mentioned that other techniques for the processing of inference problems exist. Depending on the concrete application, these methods may be less or more efficient than the class of algorithms presented in this book. But we also point out that it is in general not possible to apply these techniques to arbitrary valuation algebras, because they usually require more information about the concrete buildup of formalisms. A popular class of such algorithms are search methods, see for example (Nilsson, 1982; Pearl, 1984; Kanal & Kumar, 1988; Dechter, 2003). Search methods work through a search space that is obtained from a knowledgebase by assigning different values to variables. It is therefore clear that search methods are suitable only for formalisms that consist of mappings from finite variable assignments to some values. In particular, this covers the large family of semiring valuation algebras introduced in Chapter 5, but we will also meet numerous formalisms in this book that do not provide this structure. Search methods and local computation have also been combined to hybrid methods (Larrosa & Dechter, 2003; Dechter, 2006). A closely related aspect concerns the representation of valuations. This is again specific to each family of valuation algebras and goes along with tailored inference methods. Important techniques are AND-OR search (Dechter & Mateescu, 2007; Marinescu & Dechter, 2009a; Marinescu & Dechter, 2009b), OR search with caching (Bacchus et al., 2003), methods based on automata (Vempaty, 1992; Fargier & Vilarem, 2004), decision diagrams (Wilson, 2005; Nicholson et al., 2006) and various other techniques related to knowledge compilation (Darwiche, 2001; Darwiche & Marquis, 2001; Darwiche & Marquis, 2002; Wachter & Haenni, 2006; Fargier & Marquis, 2007; Wachter et al., 2007; Wachter, 2008). We further restrict ourselves to exact inference in this book. There are several methods to perform approximated inference with local computation as for example the mini-bucket scheme (Dechter & Rish, 2003). We further refer to (Haenni, 2004) for approximate inference with ordered valuation algebras and to (Kohlas & Wilson, 2008) for semiring valuation algebras. It should also be mentioned that other algebraic frameworks for generic inference exists, e.g. (Pralet et al., 2007), but these systems generally include the valuation algebra framework. Finally, it has already been mentioned in the first publications about local computation that these algorithms qualify for an implementation on distributed and parallel computing environments. In particular, local computation is successfully applied for inference in sensor networks (Paskin et al., 2005). This raises many interesting questions that go beyond the scope of this book. Examples are the management of computing resources, the minimization of communication costs (Pouly, 2008) or the increase of parallelism. These questions are discussed for probabilistic reasoning in (Kozlov & Singh, 1994; Kozlov & Singh, 1996; Namasivayam & Prasanna, 2006; Yinglong & Prasanna, 2008), and we also refer to the comprehensive literature on parallel and distributed databases.
