CHAPTER 7

LANGUAGE AND INFORMATION

Information often concerns the values of variables or the truth of propositions satisfying equations or logical formulae. It is in many cases stated through linguistic constructs with a determined interpretation. This general situation is a source of many valuation algebras that all have the interesting property of idempotent combination. Moreover, they always provide neutral and null elements and therefore adopt the structure of an information algebra according to Section 4.2.1. In such cases, the computations are usually not carried out on the level of the information or valuations, but rather in the corresponding linguistic system using syntactic procedures. In this chapter, we illustrate the general concept of representing information by formal languages with a determined interpretation. We first give two important examples of such formalisms and then derive a more general concept that serves as a generic construction to produce the two previous examples and many other instances.

In the first section, we show how propositional logic serves to state the truth about propositions or logical variables. The interpretation of propositional formulae represents the information expressed by the formulae. We shall show that such pieces of information form a valuation algebra and more particularly an information algebra. The second example presented in Section 7.2 concerns systems of linear equations whose solutions provide information about the values of a set of variables. Their solution spaces are again shown to form an information algebra, and the exploitation of this algebraic structure leads to sparse matrix techniques for the solution of sparse linear systems, see Chapter 9. In this chapter, we only focus on the algebraic properties of linear equation systems. Although we consider fields instead of semirings, this nevertheless is closely related to the path problems of the foregoing chapter that also require the solution of particular equation systems. We therefore move the discussion of the computational aspects of all these applications to Chapter 9. Finally, the concluding section of this chapter presents the abstract generic framework generalizing both linguistic systems. There, we also allude to some further important instances that emerge from this new generic construction.

7.1 PROPOSITIONAL LOGIC

Propositional logic or sentential calculus is concerned with the truth of elementary propositions or with the values of Boolean variables. With regard to information, the question addressed by this formalism is which propositions or variables are true and which are false. Such truth values are usually expressed by ‘1’ for true and ‘0’ for false, but the available information regarding these values may also be expressed in the propositional language. In most cases, these expressions are much simpler and shorter than the explicit enumeration of all possible truth values for the variables under consideration. Subsequently, we define this formal language and equip it with an interpretation to show how propositional information (i.e. the information about the truth values of Boolean variables) is expressed. We then point out in the following section that a dual pair of valuation algebras arises from the language and its interpretation.

7.1.1 Language and Semantics

The language of propositional logic is constructed over a countable set of propositional symbols or propositional variables . It consists of well-formed formulae (wff) defined inductively as follows:

All wffs are generated from atomic formulae by finitely many applications of the rules 2, 3 and 4. The construction 4 is usually not part of the propositional language, but it suits our purposes. The symbol is called existential quantifier. We conclude from these considerations that any wff has finite length and contains only a finite number of propositional symbols. For simplification, it is also common to extend this language by adding the following constructions:

The intended meaning of these constructions is given by the interpretation of the formulae defined below. But before doing this, let us remark that we often consider propositional languages over subsets q p. In particular, we often limit ourselves to finite subsets q of propositional symbols. So, is defined as above by replacing p in Rule 1 by q. The subsets of p form a lattice under inclusion with intersection as meet and union as join, see Example A.2 in the appendix of Chapter 1. This lattice structure is also reflected in the family of languages as follows:

In particular, we have for the language without propositional symbols.

We now give meaning to this language by interpreting its wffs. This is achieved by mappings v: p → {0, 1} which are called valuations. Here, valuations do not correspond to elements of a valuation algebra but to the traditional name of an assignment of truth values to propositions which is equivalent to the notion of tuple, configuration or vector of Chapter 1. However, we accept this double sense for a short while and always explicitly refer to the valuation algebra when the context changes. Valuations are extended to propositional formulae by:

Here, denotes the formula obtained from f by replacing all occurrences of the proposition P p by ⊥. Similarly, refers to the formula obtained from f by replacing all occurrences of P by ⊥.

If we read ‘1’ as true and ‘0’ as false, we then see that the connector represents the negation of a propositional formula, i.e. the truth value is the opposite of . The connector expresses the logical and or logical conjunction: f g is true if, and only if, both formulae f and g are true. The existential quantifier P means that the quantified formula (P)f evaluates to true, if f evaluates to true when P is either replaced by ⊥ or in f. In other words, f is true if it is true with P either interpreted as true or false. The evaluation of the formulae of the extended language follow from these definitions:

f g is interpreted as the logical or or the logical disjunction. The expression f → g is called implication and means that if f is true, then so is g. Finally, f ↔ g expresses the equivalence between f and g, i.e. f and g are either both true or both false.

Example 7.1 We describe the full adder circuit of Figure 2.7 from Instance 2.4 in the language of propositional logic over p = {In1, In2, In3, Out1, Out2}. The XOR gates in Figure 2.7 output 1 if, and only if both inputs have different values. This can be modeled by the propositional formula . We then have . Otherwise, we have . Using this construction, the full adder circuit is completely described by the following formulae:

(7.1)

and

(7.2)

A valuation v satisfies a propositional formula f if . Then, v is called a model of f, and we write . The set of all valuations satisfying f is denoted by

More generally, denotes the set of valuations which satisfy all formulae f S,

Conversely, denotes the set of all wffs which are satisfied by a valuation v,

Thus, v is a model of each element of . This notation is again extended to sets of valuations: If M is a set of valuations, then is the set of all sentences satisfied by all valuations in M,

Let denote the set of all valuations v: p → {0, 1}. A tuple consisting of a language , a set of models and a satisfying relation is called a context. This concept will be generalized in Section 7.3.1.

A formula f is called satisfiable, if there is at least one valuation v that satisfies f, i.e. if . Checking the satisfiability of a formula is the fundamental problem of propositional logic (see Instance 2.4). Two formulae f and g are called (logically) equivalent if they have the same models, i.e. if . Note that (P)f is always equivalent to a formula where the proposition P p does not occur anymore. So, existential quantification serves to eliminate variables from a formula. Similarly, two sets of formulae S1 and S2 are equivalent, if . We denote by the set of formulae for all f S. It is equivalent to a set of formulae without the variables Pi1 to Pin.

Example 7.2 The valuation v(In1) = v(Out1) = 1 and v(In2) = v(In3) = 0 satisfies the propositional formula (7.1) and is therefore called a model of this formula. On the other hand, the assignment v(Out1) = 1 and v(In1) = v(In2) = v(In3) = 0 does not satisfy the formula. If S consists of the two formulae (7.1) and (7.2), the set of valuations satisfying both formulae is given in Table 2.8 of Instance 2.4.

In the next section, we describe how these concepts are used to capture propositional information and how two dual information algebras are related to propositional languages and models.

7.1.2 Propositional Information

The available information concerning propositional variables is usually expressed by sets of propositional formulae. More precisely, a set of propositional formulae S determines the information , and the formulae S say that the unknown model, sometimes called a possible world, is a member of . With respect to the above adder example, the equations (7.1) and (7.2) specify the possible configurations (Table 2.8) of the circuit variables, if the components of the adder work correctly.

In order to move towards a valuation or even an information algebra, we consider the lattice D of finite subsets of the countable set of propositional symbols p. Any subsets q p represents a question, namely the question about the truth values of the propositions Pi q. The projection of a valuation v: p → {0, 1} is called an interpretation of the language . Let be the set of all possible interpretations of . This is a finite set of 2|q| elements. As mentioned before, the elements of Mq can also be considered as Boolean q-tuples or configurations m: q → {0, 1}. If f is a wff from , it contains only propositional symbols from q. For we write and . In other words, m is a model of f with respect to the variables in q. The values of v on variables outside q clearly do not influence the relation . We thus have for all q D a context and we next extend the notions of and to interpretations or models in and formulae in . If S is a set of formulae and M a set of models, we have

and

is called the propositional information of S with respect to q, and is the theory of M in q. The information sets, i.e. the subsets of for all q D, form an information algebra. In fact, this formalism corresponds to the relational algebra of Instance 1.2 where all relations M are Boolean. Given an information set M, we define its label by d(M) = q if M . Combination is defined by natural join. If M1 is labeled with q and M2 with u we have

(7.3)

Finally, projection of an information set M to some domain q d(M) is defined by

(7.4)

The neutral element for the domain q p is , and the null element corresponds to the empty subsets of .

Example 7.3 Let S1 and S2 denote the two singleton sets containing the adder formula (7.1) and (7.2) respectively. We identify their model sets and which are information sets with domain d(M1) = {In1, In2, In3, Out1} and d(M2) = {In1, In2, In3, Out2}:

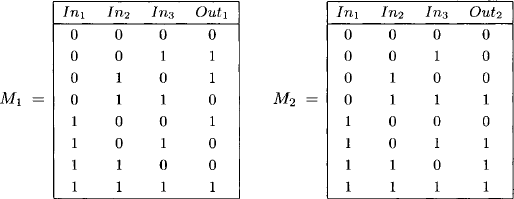
The combination M1 M2 again corresponds to the information in Table 2.8.

To this algebra of information sets, we may associate a corresponding algebra of sentences. For that purpose, we show how the above rules for combination and projection can be expressed by sentences. Consider an information described by a set S1 of wffs in and an information described by . We observe that S1 and S2 may also be seen as formulae of the language . Further, let

be the cylindric or vacuous extension of M to q ∪ u. Then, if , we also have and therefore

The last identity follows immediately from the definition of . Thus, combining pieces of information means to take the union of their defining sentences. Further, if is a set of models with for some set of sentences , it holds for q u that

where u – q = {Pi1 … Pin}. This shows that projection or extraction of information corresponds to the existential quantification of the sentences describing the original information. In this way, an algebra of formulae is associated to the algebra of models. In fact, to each model set of its theory is associated. The operator satisfies the axioms of a closure operator (Davey & Priestley, 1990). This will be proved in the general context in Lemma 7.2 of Section 7.3 below. Subsets S with S = Cq(S) are therefore called closed. Clearly, implies that and therefore . Thus, theories Cq(S) are always closed sets, and the algebra of formulae is in fact an algebra of closed sets of formulae. Combination between closed sets S1 and is defined by

(7.5)

and projection of a closed set to some subset q u by

(7.6)

where u - q = {Pi1 … Pin}. The neutral elements in this algebra are the tautologies Cq(), whereas the null elements equal the whole language . Both are clearly closed sets. This algebra of closed sets is closely related to the well-known Lindenbaum algebra of propositional logic (Davey & Priestley, 1990) which is a Boolean algebra that covers combination but not projection. Our algebra is a reduct of the Lindenbaum algebra as a Boolean algebra, but extended by the operation of projection.

To conclude this section, we formalize the relations between contexts cq for different q D. If u q, then any wff is also a wff in . Formally, we define this embedding simply by the identity mapping fu,q(s) = s. On the other hand, models m can be projected to Mu. We therefore define the projection mapping by . Then, the pair of contravariant mappings fu,q and gq,u clearly satisfies the following property:

Such a pair of contravariant mappings is called an infomorphism between the contexts cq and cu (Barwise & Seligman, 1997). They are considered in a more general and abstract setting in Section 7.3 below.

7.1.3 Some Computational Aspects

The formalism of propositional logic induces a dual pair of valuation algebras that arises from the language and its interpretation. In the first case, valuations are closed sets of formulae and their rules of combination and projection are given in equations (7.3) and (7.4). In the second case, valuations are sets of models and their operations of combination and projection are given in equations (7.5) and (7.6). The proof that the valuation algebra axioms are satisfied in both systems will be given in a more general context in Section 7.3.2 below. Hence, inference problems with knowledgebases from propositional logic can be computed by the local computation architectures of Chapters 3 and 4. We now give two important examples of such inference problems.

7.1 Satisfiability in Propositional Logic

Let {(1, …, n} Φ be a set of propositional information pieces, either represented in the valuation algebra of closed sets of formulae or in the valuation algebra of model sets. In any case, this set is interpreted conjunctively, i.e. the objective function = 1 … n is satisfiable if, and only if, each factor i with i = 1, …, n is satisfiable. A satisfiablity test therefore reduces to a single-query inference problem with the empty set as query:

Assume that we work on the language level. If we obtain the tautology then the knowledgebase is satisfiable. Otherwise, if then the knowledgebase is contradictory. If we work on model level, then indicates a satisfiable knowledgebase and a contradictory knowledgebase.

7.2 Theorem Proving in Propositional Logic

Let {1, …, n} Φ be a set of propositional information pieces and a hypothesis. Testing whether the hypothesis is true under the given knowledgebase is equivalent to verifying whether is contradictory. This induces an inference problem according to the foregoing instance. Here, denotes the negation of the hypothesis. Depending on the knowledgebase, this is either expressed in the valuation algebra on language or on model level.

If some propositional information over the variables q p is expressed by a set of formulae S , then the corresponding valuation on language level is the closed set of formulae Cq(S). Closed sets of a set of formulae correspond to their theory and are infinite constructs. For practical applications, it is therefore essential to work with some finite representation of Cq(S), most appropriately with some normal form of S. It is then important that the valuation algebra operations can be expressed with respect to the chosen normal form. This requires that executing a combination or projections again leads to a corresponding normal form. There are many different normal forms that could be used (Darwiche & Marquis, 2001). As an example, we use the conjunctive normal form.

A positive literal P p is a prepositional variable and its negation -P is called a negative literal. A clause is a disjunction of either positive or negative literals li for i = 1, …, m, i.e. . Such clauses are called proper if every propositional variable appears at most once. A formula is in conjunctive normal form (CNF) if it is written as a conjunction of proper clauses, i.e. where i are proper clauses for i = 1, …, n. It is known that every formula can be transformed into an equivalent CNF (Chang & Lee, 1973) and because sets of formulae are interpreted conjunctively, we may also transform sets of formulae into a CNF. It is common to represent CNFs as clause sets Σ = {1, …, n}, which henceforth are used as normal form. Following (Kohlas et al., 1999) we define the combination of two clause sets Σ1 and Σ2 by

(7.7)

Here, μ denotes the subsumption operator that eliminates non-minimal clauses. This means that if all literals of some clause are contained in another clause, then the second is a logical consequence of the first and can be removed. We observe that if , the result of this combination is again a clause set whose closure satisfies

(7.8)

For the definition of projection it is more suitable to switch to variable elimination. We first remark that every clause set Σ, obtained from a set of formulae , can be decomposed into disjoint subsets with respect to a proposition X u:

This is possible because Σ contains only proper clauses. Then, the elimination of a variable X u is defined by

(7.9)

where

(7.10)

is the set of resolvants between clauses in ΣX and . We again observe that the result of this operation is a clause set. Moreover, equation (7.9) corresponds to existential quantification with respect to the proposition X u, such that we have

(7.11)

see (Kohlas et al., 1999). Clause sets are closed under combination (7.7) and variable elimination (7.9). Because further the equations (7.8) and (7.11) hold, we conclude that clause sets form a valuation algebra. A direct proof of this statement can also be found in (Haenni et al., 2000). The following example illustrates the computation with propositional clause sets.

Example 7.4 Consider the propositional variables p = {U, V, W, X, Y, Z} and two clause sets Σ1 and Σ2 defined as

Combining Σ1 and Σ2 gives

Observe that the variable U p is contained in Σ2 but disappears in the combination. This seems to contradict the labeling axiom of valuation algebras. However, it does not because p - {U} p implies that . This allows us to consider Σ1 Σ2 as a valuation with domain d(Σ1 Σ2) = p. To eliminate variable X p we partition the clause set as follows:

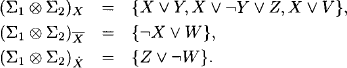
We then obtain

For practical purposes, the use of the CNF normal form is often unsuitable since clause sets may be very large. We therefore prefer a more compact representation as for example prime implicates. A proper clause is called implicate of a sentence . An implicate of γ is then a prime implicate if no proper subclause of is also an implicate of γ. In other words, prime implicates of some sentence γ are the logically strongest consequences of γ. The set of all prime implicates of γ defines a conjunctive normal form denoted by Φ(γ). It is therefore possible to apply the above rules of combination and projection to sets of prime implicates, if we additionally change the μ operator in such a way that the result is again a set of prime implicates. We refer to (Haenni et al., 2000) for a discussion of computing with prime implicates and other normal forms of propositional logic.

7.2 LINEAR EQUATIONS

The second formalism we are going to consider are systems of linear equations over sets of variables. We examine the solution spaces of such systems and introduce operations between solution spaces that are also mirrored by corresponding operations on the systems of linear equations. This program needs some notational conventions and we also remind some basic elements of linear algebra.

7.2.1 Equations and Solution Spaces

We consider an index set r of a set of variables which, in the interest of simplicity, is assumed to be finite, although the following discussion could be extended to a countable set without much difficulty. For a subset s r and we define a linear system of m equations

(7.12)

for i = 1, …, m. The number of equations m can be smaller, equal or larger than the number of variables |s|. Note that such equations are purely syntactic constructs. They obtain a meaning, if we specify the coefficients ai,j and bi to be real numbers. Then, we are looking for real values for the variables Xj that satisfy the above equations, when the arithmetic sum and multiplication are used on the left-hand side. These assignments again correspond to real s-vectors such that

for i = 1, …, m. Any s-vector that satisfies this relation is called a solution to the linear system. There may be no solution, exactly one solution or infinitely many solutions. We consider the set of solutions of the system (7.12) as the information expressed with respect to the variables involved, and refer to it as the solution space of system (7.12).

In order to discuss solution spaces of linear systems in general, we need to remind some basic facts of linear algebra. The s-vectors form a linear space where addition is defined component-wise, i.e. x + y has components xi + yi for i s, and scalar multiplication c · x of x with a real value c has components c · xi. The linear space of s-vectors is denoted by and its dimension equals |s|. Similarly, for , we define m-vectors by mappings which also form a linear space with component-wise addition and scalar multiplication. This linear space of dimension m is denoted by . Finally, the m × s matrix A of the linear system (7.12) is a mapping {1, …, m} × s → with components ai,j for i {1, …, m} and j s. It defines a linear mapping determined by the matrix-vector product for . The mapping is linear since A(x + y) = Ax + Ay and A(c · x) = c · Ax. Its range is the set of all vectors in m which are images of s-vectors in ,

The range is a linear subspace of m and therefore has a determined dimension dim() called the rank of A. We subsequently write rank(A) for the rank of the linear mapping A which corresponds to the maximal number of linearly independent rows or columns of A. The null space of the mapping A is the set of s-vectors that map to the zero vector 0 m,

This is again a linear space, a subspace of s with a determined dimension dim(). A well-known theorem of linear algebra states that

(7.13)

Thus, a linear mapping is associated to every system of linear equations determined by the matrix of the system. The solution space of the linear system can be described in terms of this mapping: If y is a solution of (7.12), i.e. Ay = b, then clearly y + x0 is a solution of (7.12) for any , and any solution can be written in this form. The solution space of (7.12) is therefore

The solutions to (7.12) are thus determined by a particular solution y to the linear system and the set of solutions to the corresponding homogeneous system AX = 0. A set y + , where y is an s-vector and is a linear subspace of s, is called an affine space in s. Its dimension equals the dimension of . So, the solution spaces of linear equations over variables in s are affine spaces in s. The following example illustrates these concepts by a linearly dependent, under-determined system:

Example 7.5 For a set of variables {X1, X2, X3} consider the linear system:

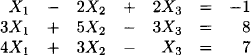
We have |s| = m = 3 and the associated matrix determining the linear mapping is:

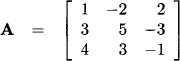
This equation system is linearly dependent because the third equation corresponds to the sum of the two others. We have rank(A) = dim() = 2 and according to (7.13) dim() = 1. Transforming A into a lower triangular matrix by subtracting the triple of the first row from the second row, and by subtracting the sum of the first two rows from the third, gives

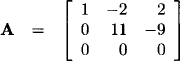
Thus, we may describe the null space of the linear mapping represented by A as

A particular solution to the original system is: X1 = 1, X2 = 1 and X3 = 0. We can therefore describe the solution space by

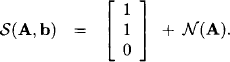
There are four possible cases to be distinguished at this stage:

In the first case, the system (7.12) has a solution for any m-vector b, since = m, and it follows from (7.13) that . Consequently, the solution space has dimension dim((A)). In the second case, the system (7.12) has solutions only if b . Then, the solution space is an affine space of dimension dim((A)) > 0. In the third case, we see that dim((A)) = 0 according to (7.13). So, if the system (7.12) has a solution, it is unique. The solution space is a point, and it has a solution if b . If |s| = m, then this is automatically the case. Finally, in the fourth case, we again have dim((A)) > 0 and solutions exist, if and only if, b . The solution space again has dimension dim((A)). Example 7.5 presents a system in this case. So, solution spaces of systems (7.12) are either empty or affine spaces in s. It is convenient to consider the empty set also as an affine space in s. Then, solution spaces are always affine spaces without exception. Conversely, we remark that any affine space y + in s is the solution space of some linear system over variables in s. This is another well-known result from linear algebra, and it clarifies the relation between affine spaces in s and systems of linear equations over a set s of variables.

We now look at systems of linear equations and solutions in a way similar to the propositional logic case in the previous section. Consider syntactic constructions like

with ai and b being real numbers. Such single equations are the sentences or formulae of a language s defined over the variables Xi with indices from a set s r. If an s-vector x is a solution of such an equation e, we write which defines a binary relation . We now consider the structure and reformulate the above discussion about systems of linear equations in terms of this structure: For an equation be the set of all solutions to this equation,

If is a set of equations, then denotes the set of all solutions to the equations in E,

If E is a finite set, then is an affine space. Conversely, we may look for all equations having a given s-vector as solution,

Similarly, for a set M s of s-vectors,

is the set of equations for which all elements of M are solutions. We observe that

These concepts allow us to derive and express some well-known facts from linear algebra: first, two systems E and E′ of linear equations are called equivalent, if they have the same solution space, i.e. if, and only if, . Then, E’ E is called a minimal system, if and there is no subset E" E’ such that . For any set of equations E, and thus also for any affine space y + , there clearly exist such minimal systems E’. They are characterized by the property that their matrix A’ has full rank m, where m = |E’| ≤ |s| is the number of equations in E’. In fact, if rank(A) < m ≤ |s|, then the equations are linearly dependent, and we may eliminate m - rank(A) of them to get an equivalent system with matrix A’. We then have . We may likewise eliminate m - r equations if the system has rank r. Further, if M is a subset of an affine space y + then , hence . If equality holds, then M is said to span the affine space y + . In any case, is itself an affine space spanned by M. It is also clear that y + spans itself, so that must hold. For any affine space y + there are minimal sets M which span the affine space, and the cardinality of these minimal sets equals the dimension of the affine space.

Structures of systems of linear equations over sets of variables s r may of course be considered for any non-empty subset s r. The relations between these structures for different subsets will next be considered. Assume t s. Then, any equation with

may also be seen as an equation in via the embedding

where ai = 0 if i s - t. Also, s-vectors x may be projected to the subspace t. This projection is denoted by gs.t and defined component-wise for i t by

We observe that if the s-vector x is a solution of the equation ft,s(e), then the t-vector gs,t(x) is a solution of the equation e and vice-versa. It therefore holds that

Subsequently, we again write for the projection of an s-vector to t s. Hence, the contravariant pair of mappings ft,s: s → t and gs,t: s → t have the same property as the corresponding mappings introduced for prepositional logic in Section 7.1. They form again an informorphism. This hints at some common structure behind the two systems of prepositional logic and linear equations which will be discussed in Section 7.3. Here, we continue by showing that affine spaces form an information algebra. This yields a foundation for discussing local computation techniques for the solution of linear systems in Chapter 9.

7.2.2 Algebra of Affine Spaces

Let r be a finite index set and D its lattice of subsets. We denote by Φs the family of affine spaces in the linear space s where for is the only affine space. We further define

and introduce within this family of affine spaces the operations of labeling, combination and projection. Note that the affine spaces in s represented by y + ’ und y’ + are identical, if and y - y’ .

The labeling operation is simply defined by d() = s if = y + is an affine space in s, i.e. is a linear subspace of s. For the combination of two affine spaces in s and t, we first extend them to and compute their intersection. So, let us define the extension of an affine space: If is an affine space with d() = s and s t, then

We show that is again an affine space: From = y + and we conclude that for some x0 . This implies that with

where 0 denotes the zero vector for the domain t – s and

It is easy to verify that is a linear space since and . Therefore, is an affine space in t which finally allows us to define the combination between an affine space ψs and an affine space ψ Φt:

This is again identical to the operation of natural join in the relational algebra:

It remains to verify that ψ is still an affine space which follows immediately from the following argument: Let be represented by a system of linear equation E over variables in s, and ψ by a system E’ over variables in t. Then, the solution space of the union E E’ of these two systems is clearly , hence an affine space.

For the definition of projection let = y + be an affine space in s and t s. The projection is defined as in the relational algebra by

Since x implies that x = y + x0 for some x0 , we obtain and therefore

Clearly, is a linear subspace of t and therefore an affine space in t.

Altogether, the algebraic structure (Φ, D) with the operations of labeling, combination and projection is well-defined. Combination has s as a neutral element in domain s and the empty set as null element. Thus, we see that affine spaces form a subalgebra of the relational algebra of s-vectors and therefore inherit the properties of an information algebra. In other words, affine spaces provide another instance of an information algebra and are therefore amenable to the application of local computation. However, we generally cannot compute with affine spaces directly, since they are infinite sets. Instead, we revert to finite representations of them through systems of linear equations. We refer to Chapter 9 for such computational aspects. Finally we note that the above discussion also applies to linear equations over arbitrary fields. This identifies another generic construction that produces a new information algebra for each field. Particularly important among them are Galois fields that have many important applications in coding theory.

7.3 INFORMATION IN CONTEXT

In the previous two sections, we described the two rather different formalisms of propositional logic and systems of linear equations. Different as they are, we have nevertheless worked out some common features. Essentially, information as set of models or set of vectors is represented or described by sentences of some formal language, and sets of such sentences determine the information described by them. In this section, we examine the abstract structure behind both formalisms that leads to a further generic construction for obtaining information algebras.

7.3.1 Contexts: Models and Language

We introduce an abstract concept called context that represents the connection between language and information. Here, language refers to a very simple form of a formal language such as the language of propositional logic or linear equations. For our purposes, it is sufficient to represent a language by the set of its sentences without regard to the syntactic structure of these sentences. In general terms, information concerns a question of interest which formally is represented by the set of its possible answers denoted by M. In the example of propositional logic M is the set of interpretations of propositions. In the case of linear equations over variables of an index set r, M is the set of r-vectors. We refer to the elements of M as models and further assume a binary relation . For a pair we write . In propositional logic this means that model m satisfies formula s. For linear equations it means that vector m is a solution to equation s.

A triple is called a context and serves to express information by sentences: If is a sentence, then

is the set of models satisfying s, which is thought of being the information described by stating s. If ,

is the set of models satisfying all sentences of S or the information expressed by S. Similarly, is a model, then

is the set of sentences satisfied by m. And if is a set of models, then

is the set of sentences satisfied by all elements of M. It can be considered as the theory of M, i.e. the set of all sentences which express M.

It is important to note the formal duality between the concepts derived from and . This is emphasized by the following lemma which collects some elementary properties of these mappings between the power sets of and :

Lemma 7.1 Let and be the above operators for a context . Then if S, Sj and M, Mj , the following dual pairs of properties hold:

Proof: We prove the properties for the language part. The corresponding results for the model part follow by duality.

We next introduce the operators

We remark that means that for all m which are models of S. In logic, such a relation is called a logical consequence, and it is said that s is a logical consequence of S, written as . So, is the set of all logical consequences of S. We therefore call a consequence operator. Similar relations hold for the operator on the model side. The following dual properties of consequence operators follow immediately from Lemma 7.1:

Lemma 7.2 For the consequence operators and in , and S and M the following properties hold:

Operators satisfying these three conditions are called closure operators and play an important role in the foundations of logic and in topology (Wojcicki, 1988; Norman & Pollard, 1996). We already came across closure operators in the context of Kleene valuation algebras in Chapter 6. Sets S and M such that and are called closed. Closed sets of sentences and models can be understood in the following sense: if a set S of sentences is stated, then is by Property 3 of Lemma 7.1 a closed set of models representing the information expressed by S. We therefore call a closed sets of models an information set or shortly, an information. In particular, is the information expressed by S. The closure of S is the set of all logical consequences of S called its theory. Similarly, if M is an arbitrary set of models, is a closed set of sentences called the theory of M. Any set M of models determines an information set . Note that is a map and is a contravariant map to . This pair of contravariant mappings satisfies the property that

(7.14)

This follows from Property 1 and 2 of Lemma 7.1. A contravariant pair of mappings satisfying (7.14) is an instance of a Galois connection. We mention that such structures are also used in formal concept analysis (Davey & Priestley, 1990).

It is time to illustrate and to link these abstract concepts with the examples of the previous two sections, as well as with some additional examples. In Section 7.3.2 it will then be shown that these formalisms satisfy the axioms of an information algebra under some additional assumptions. They are therefore new instances of our generic framework.

7.3 Propositional Logic

Section 7.1 introduced the language and interpretation of propositional logic. Models are valuations v of propositional symbols and serve to interpret propositional formulae. More precisely, v s holds if the formula s evaluates to true under the valuation v, i.e. if . If we restrict ourselves to finite sets q of propositional symbols, then all sets of models are closed. The closure operators Cq correspond to the consequence operators C in the abstract setting above.

7.4 Linear Equation Systems

Another example is provided by systems of linear equations discussed in Section 7.2. The language is formed by linear equations e over variables from an index set s with coefficients in a field, for example in the field of real or rational numbers. Models x are s-tuples with values in the field. The relation x e means that the s-tuple x is a solution to the equation e. In case of real numbers, the closed sets of models are exactly the affine spaces in s. Note that an affine space of dimension k is spanned by k linearly independent vectors. The affine space spanned by a set of vectors M is the closure of M. The theories C(S) are formed by the totality of equations sharing the same affine space as solutions with the set S.

7.5 Linear Inequality Systems

Instead of linear equations, we may also consider linear inequalities

over variables with indices from a set s and real-valued coefficients ai and a0. Such formulae are the elements of the language, and models are again s-vectors x. The relation x e holds if x satisfies the inequality e, i.e. if

Closed sets of models are convex polyhedra in the vector space s and, as we will see below, form an information valuation algebra. Systems of linear inequalities are especially used in linear programming (Chvátal, 1983; Winston & Venkataramanan, 2002).

7.6 Predicate Logic

A further example in the domain of logic is provided by predicate logic. The vocabulary of predicate logic consists of a countable set of variables X1, X2, … and a countable set of predicate symbols P1, P2, … and further includes the logical constants and and the connectors . Each predicate symbol Pi has a definite rank ρi, and a predicate with rank ρ is referred to as a ρ-place predicate. Formulae of predicate logic are built according to the following rules:

The predicate language consists of all formulae which are obtained by applying these rules a finite number of times. We consider also the predicate language s where only variables from a subset s of variables are allowed. Often, s is restricted to be a finite set.

In order to define an interpretation for formulae of predicate logic, we choose a relational structure = (U, R1, R2, …) where U is a nonempty set called universe, and the Ri are relations among elements of U with arity ρi equal to the rank of predicate Pi. In other words, Ri are subsets of Uρi. A valuation is a mapping v: {1, 2, …} → U which assigns to each variable Xi a value v(i) U. We write Uω for the set of all possible valuations. Given a valuation v and an index i, we define the set of all possible valuations that agree with v on all values except v(i),

Valuations v are used to assign a truth value to formulae f . This assignment is defined inductively as follows:

A valuation v is called a model of a formula f in the structure if . We then write v f. This defines the relation between formulae of and valuations in Uω. Further, the relation can be restricted to languages s and s-tuples m in Us which are simply projections of valuations v to subsets s. In this case, we write m s f. Information sets then are subsets of Us, i.e. relations in s. They form the relational algebra over subsets s which exhibits the close and well-known relation of predicate logic to relational algebra and hence to relational databases. We refer to (Langel, 2010) for more details about predicate logic and information.

Besides propositional and predicate logic, many other logic systems possess this context structure. We refer to (Wilson & Mengin, 2001) for further instances from the field of logic.

Two sets of sentences S1 and S2 are called equivalent, if they have the same models, . This means that S1 and S2 express the same information and it is equivalent to saying that they have the same theories . Any set S of sentences is in particular equivalent to its theory . In the same way, two sets of models M1 and M2 are equivalent, if they have the same theory . They span the same information (see for example Instance 7.4).

In a first step towards a valuation algebra, we may already discuss a preliminary concept of combination of information. In fact, suppose two sources which both send a piece of information by stating sets S1 and S2 of sentences. They express the two information sets and . On the level of sentences, combining these two pieces of information means clearly putting the two sets of sentences together as S1 ∪ S2. Think for example of two systems of linear equations. On the model level, the combined information is then given by the models of S1 ∪ S2. Hence, we may tentatively define the following combination operation between two information sets:

Using Property 4 of Lemma 7.1 we may also write this operation as:

Combining two information sets simply corresponds to set intersection. It thus follows that the intersection of two closed sets is again a closed set. In fact, since Property 4 of Lemma 7.1 holds for any family of sets Sj, we conclude that the intersection of any family of closed sets is again a closed set. From this, it follows by a standard results of lattice theory that closed sets form a complete lattice (see Definition A.5) (Davey & Priestley, 1990). This is a fundamental result of context analysis. We are pursuing however a different direction. In the following section we shall construct an information algebra out of context systems.

7.3.2 Tuple Model Structures

In all examples we have seen so far, we dealt with subsets s of variables, and the models were valuations of these variables in some sets, for example real numbers as in linear systems of equations or Boolean values as in prepositional logic. For every subset of variables we have a context cs linking the sentences or formulae with the corresponding values, for example as solutions to sets of linear equations or interpretations satisfying prepositional formulae. These contexts are linked together by projection of models and embeddings of sentences. In this section, we subsume this situation into an abstract frame which induces a generic construction producing these examples as particular instances. In a first step, we abstract the structure of s-vectors and interpretations (Boolean vectors) into a general abstract frame called tuple system. In fact s-vectors and s-interpretations for subsets s of a set r of variables are instances of a tuple system defined as follows:

Definition 7.1 A tuple system over the lattice D of subsets s r is a set T together with two operations d: T → D and defined for × d(f) which satisfies the following axioms: For f, g T and x, y D,

The operation ↓ of course corresponds to the projection of s-vectors, and the label d indicates to which group of variables a vector or tuple belongs. Vectors and ordinary tuples as occurring in relational databases are evidently instances of abstract tuples according to the definition above.

Example 7.6 The relational algebra of Instance 1.2 can be generalized to abstract tuple systems. Then, a relation R over s D is a set of tuples f T which all have the domain s. This also defines the label of R as d(R) = s. Combination of two relations R1 and R2 with domains s and t respectively is defined by natural join,

and projection of relation R with domain s to t s is defined as

Verifying that this generalized relational algebra also satisfies the valuation algebra axioms is similar to the ordinary relational algebra.

The algebra of models in Section 7.1 corresponds to such a generalized relational algebra over Boolean tuples. The algebra of affine spaces in Section 7.2 is a subalgebra of the relational algebra over s-vectors, and the same holds for the algebra of convex polyhedra in Instance 7.5. Here follows a more unusual example.

Example 7.7 Let be an idempotent valuation algebra, i.e. for Φ and x d() it holds that

We further assume a neutral element ex for each domain × D, and that the valuation algebra is stable, i.e. that for y x. Then Φ is a tuple system: The properties 1, 2 and 3 of a tuple system simply correspond to the Axioms (A3), (A4) and (A6) of the valuation algebra. To verify Property 4, assume d() = x, d(ψ) = y and . Defining χ = ψ, we obtain from the combination axiom (A5) and idempotency that

In a similar way, we derive χ↓y = ψ. For Property 5, let d() = x and χ = ey. It follows that d(χ) = y and by the combination axiom and the property assumed for neutral elements that

This shows that each idempotent valuation algebra with neutral elements adopts itself the structure of a tuple system.

As in the above examples, we now link tuples systems with formal languages to form a family of contexts. For that purpose, remember that the contexts for all x r in the examples are linked together by embedding and projection mappings. Thus, let M be a tuple system over the subsets of a set r. We define the set of all tuples with domain x by

Further, we assume the existence of language x associated with Mx to express information in x. More precisely, we suppose a context for each subset x r, and for y x an embedding fy,x: y → x such that it forms together with the projection gx,y: x → y defined by gx,y(m) = m↓y an infomorphism. We thus have

For a set of sentences S of the language x we have the information set in x which is a x-closed set . Let Φx be the set of all x-closed sets in Mx and

We examine whether Φ adopts the structure of an information algebra relative to the lattice of subsets of r. In fact, since the elements of Φ are generalized relations, it is sufficient to show that it is a subalgebra of the generalized relational algebra associated with the tuple system M (see Example 7.6), and this requires that Φ is closed under join and projection. Unfortunately, it follows from the formal duality between languages and models that Φ is not necessarily closed under projection. This can, for example, be seen by the example of propositional logic: the embedding fy,x(S) of a theory in the context cy is not yet closed in the context cx. Dually, we may generally not expect that the projection gx,y(M) of a closed set in the context cx is still closed in cy. However, this is the case in many examples and in particular in all examples we have seen so far. Therefore we tacitly assume or require that gx,y(M) is y-closed when M is x-closed.

The situation is different for combination: Let M1 Φx, M2 Φy and recall that

(7.15)

where for M Mx and x y is defined as:

We claim that is y-closed if M is x-closed. In fact, assume that for some set of sentences S x. We then have the following equivalences due to the infomorphism property:

This shows that which is a y-closed set. Therefore, both and in equation (7.15) are -closed sets, and since the intersection of closed sets is still closed, we have .

To sum it up, Φ is a subset of the generalized relational algebra from which we already know that it satisfies the information algebra axioms. It is furthermore closed under combination and projection which turns the structure into a subalgebra of the generalized relational algebra. Therefore, also forms an information algebra. This holds for all families of contexts where the corresponding operations of embedding and projection are linked by an infomorphism, given the additional condition that the projection of closed model sets always leads to a closed model set. The algebra contains neutral elements x for all contexts x, corresponding to the tautologies in context x. This generic construction called context valuation algebra produces among other formalisms the information algebras of propositional and predicate logic, and of linear equation and inequality systems. This is shown by the following examples:

Example 7.8 In the case of propositional logic (see Section 7.1 and Instance 7.3) the tuple system consists of all Boolean s-vectors m: s → {0,1}, and Φ is equal to the relational algebra over this tuple system, if r is finite. This is because any subset of x is x-closed. The same situation is found in the predicate logic of Instance 7.6 where the models also form a relational algebra.

Example 7.9 In the context of linear equations (see Section 7.2 and Instance 7.4) the tuple system consists of all s-vectors m: s → . Here, Φ is the subalgebra of affine spaces of the relational algebra of s-vectors. As we have seen, affine spaces project to affine spaces again.

Example 7.10 Similar as in systems of linear equations, the tuple system of linear inequalities (see Instance 7.5) consists of all s-vectors m: s → . But here, Φ is the subalgebra of convex polyhedra in the linear space s. Again, convex polyhedra always project to convex polyhedra.

7.4 CONCLUSION

We started into this chapter by considering the two formalisms of propositional logic and linear equations. Both examples provide a formal language to describe their information sets. In the first case, propositional formulae describe sets of truth value assignments to propositional symbols under which the corresponding formula evaluates to true, and in the second case, linear equations describe their associated sets of solutions. This interaction of sentences and model sets uncovers two information algebras for each formalism. On the model level, both formalism correspond to (a subalgebra of) the relational algebra of Instance 1.2 and therefore adopt the structure of a information algebra. These properties mirror the context structure. Closed sets of sentences therefore also form an information algebra. Although our considerations for linear equations were limited to real numbers, we noted its applicability for arbitrary fields. This identified a first generic construction which actually produces two new information algebras for each field. However, the final section of this chapter showed that propositional logic and linear equations over arbitrary fields are instances of a far more general generic construction called context valuation algebra. Based on so-called tuple systems, this further induces the information algebra behind linear inequalities, predicate logic, and many other formalisms where this duality between language and models exists.

PROBLEM SETS AND EXERCISES

G.1 * Express consequence finding in propositional logic as an inference problem. This solution to this exercise can be found in (Inoue, 1992).

G.2 * Exercise D.4 in Chapter 4 introduced a partial order between the elements of an idempotent valuation algebra. Apply this order to propositional logic, linear equation systems and to contexts in general and explore its semantics.

G.3 ** In this chapter, we discussed propositional and predicate logic as instances of context valuation algebras. Other non-classical logics are studied in (Wilson & Mengin, 2001). Identify the context structure in these logics.

G.4 *** Context valuations are infinite constructs but with a finite representation. For propositional logic such representations could be so-called normal forms. Exemplarily, we studied the conjunctive normal form and the normal form of prime implicates in Section 7.1.3. But there are many other normal forms listed in (Dar-wiche & Marquis, 2002; Wachter & Haenni, 2006) that could be used as well. Analyse further normal forms and provide suitable definitions for combination and projection.