1
Basic Knowledge of Vehicle System Dynamics
1.1 Traditional Methods of Formulating Vehicle Dynamics Equations
Traditional methods of formulating vehicle dynamics equations are based on the theories of Newtonian mechanics and analytical mechanics. Some of the definitions used in dynamics are presented first.
- Generalized coordinates
Any set of parameters that uniquely define the configuration (position and orientation) of the system relative to the reference configuration is called a set of generalized coordinates. Generalized coordinates may be dependent or independent. To a system in motion, the generalized coordinates that specify the system may vary with time. In this text, column vector
 is used to designate generalized coordinates, where n is the total number of generalized coordinates.
is used to designate generalized coordinates, where n is the total number of generalized coordinates.In Cartesian coordinates, to describe a planar system which consists of b bodies,
 coordinates are needed. For a spatial system with b bodies,
coordinates are needed. For a spatial system with b bodies,  (or
(or  ) coordinates are needed.
) coordinates are needed.The overall vector of coordinates of the system is denoted by
 , where vector qi is the vector of coordinates for the ith body in the system.
, where vector qi is the vector of coordinates for the ith body in the system. - Constraints and constraint equations
Normally, a mechanical system that is in motion can be subjected to some geometry or movement restrictions. These restrictions are called constraints. When these restrictions are expressed as mathematical equations, they are referred to as constraint equations. Usually these constraint equations are denoted as follows:
(1.1)
If the time variable appears explicitly in the constraint equations, they are expressed as:
(1.2)
- Holonomic constraints and nonholonomic constraints
Holonomic and nonholonomic constraints are classical mechanics concepts that are used to classify constraints and systems. If constraint equations do not contain derivative terms, or the derivative terms are integrable, these constraints are said to be called holonomic. They are geometric constraints. However, if the constraint equations contain derivative terms that are not integrable in closed form, these constraints are said to be nonholonomic. They are movement constraints, such as the velocity or acceleration conditions imposed on the system.
- Degrees of freedom
The generalized coordinates that satisfy the constraint equations in a system may not be independent. Thus, the minimum number of coordinates required to describe the system is called the number of degrees of freedom (DOF).
- Virtual displacement
Virtual displacement is an assumed infinitesimal displacement of a system at a certain position with constraints satisfied while time is held constant. Conditions imposed on the virtual displacement by the constraint equations are called virtual displacement equations. A virtual displacement may be a linear or an angular displacement, and it is normally denoted by the variational symbol δ. Virtual displacement is a different concept from actual displacement. Actual displacement can only take place with the passage of time; however, virtual displacement has nothing to do with any other conditions but the constraint conditions.
1.1.1 Newtonian Mechanics
The train of thought used to establish the vehicle dynamics equations using Newton’s law can be summarized in a few steps. According to the characteristics of the problem at hand, first, we need to simplify the system and come up with a suitable mathematical model by representing the practical system with rigid bodies and lumped masses which are connected to each other by springs and dampers. Then, we isolate the masses and bodies and draw the free-body diagrams. Finally, we apply the following formulas to the masses and bodies shown by free-body diagrams.
The dynamic equations of a planar rigid body are:

where m is the mass of the body, r is the displacement of the center of gravity, Fi is the ith force acting on the body, J is the mass moment of inertia of the body about the axis through the center of gravity, ω is the angular velocity of the body, and Mi is the moment of the ith force acting on the center of gravity of the body.
1.1.2 Analytical Mechanics
In solving the dynamics problems of simple rigid body systems, Newtonian mechanics theories have some obvious advantages; however, the efficiency will be low if dealing with constrained systems and deformable bodies. Analytical mechanics theories have been proven to be a useful method in solving these problems. This theory contains mainly the methods of general equations of dynamics, the Lagrange equation of the first kind, and the Lagrange equation of the second kind; the latter being the most widely used.
For a system with b particles (or bodies), and n DOF, q1, q2, …, qn is a set of generalized coordinates. Then, the Lagrange equation of the second kind can be expressed as

where T is the kinetic energy, and V the potential energy of the system.
1.2 Dynamics of Rigid Multibody Systems
1.2.1 Birth and Development
The history of the development of classical mechanics goes back more than 200 years. In the past two centuries, classical mechanics has been successfully used in the theoretical study and engineering practice of relatively simple systems. However, most modern practical engineering problems are quite complicated systems consisting of many parts. Since the middle of the 20th century, the rapid development of aerospace, robotics, automotive and other industries has brought new challenges to classical mechanics. The kinematics and dynamics analysis of complicated systems becomes difficult. Thus, there was an urgent need to develop new theories to accomplish this task.
In the late 1960s and early 1970s, Roberson[1], Kane[2], Haug[3], Witternburg[4], Popov[5] and other scholars put forward methods of their own to solve the dynamic problems of complex systems. Although there were some differences between these methods in describing the position and orientation of the systems, and formulating and solving the equations, one characteristic was common among them: recurring formularization was adopted in all these methods. Computers, which help engineers to model, form, and solve differential equations of motion, were used analyze and synthesize complex systems. Thus, a new branch of mechanics called multibody dynamics was born. This developing and crossing discipline arises from the combination of rigid mechanics, analytical mechanics, elastic mechanics, matrix theory, graph theory, computational mathematics, and automatic control. It is one of the most active fields in applied mechanics, machinery, and vehicle engineering.
Multibody systems are composed of rigid and/or flexible bodies interconnected by joints and force elements such as springs and dampers. In the last few decades, remarkable advances have been made in the theory of multibody system dynamics with wide applications. An enormous number of results have been reported in the fields of vehicle dynamics, spacecraft control, robotics, and biomechanics. With the development and perfection of the multibody formalisms, multibody dynamics has received growing attention and a considerable amount of commercial software is now available. The first International Symposium on multibody system dynamics was held in Munich in 1977 by IUTAM. The second was held in Udine in 1985 by IUTAM/IFTOMM. After the middle of the 1980s, multibody dynamics entered a period of fast development. A wealth of literature has been published[6,7].
The first book about multibody system dynamics was titled Dynamics of System of Rigid Bodies[4] written by Wittenburg, was published in 1977. Dynamics: Theory and applications by Kaneand Levinson came out in 1985. In Dynamics of Multibody System[8], printed in 1989, Shabanacomprhensively discusses many aspects of multibody system dynamics, with a second edition of this book appearing in 1998. In Computer-aided Analysis of Mechanical Systems[9], Nikravesh introduces theories and numerical methods for use in computational mechanics. These theories and methods can be used to develop computer programs for analyzing the response of simple and complex mechanical systems. Using the Cartesian coordinate approach, Haug presented basic methods for the analysis of the kinematics and dynamics of planar and spatial mechanical systems in Computer Aided Kinematics and Dynamics of Mechanical Systems[3].
The work of three scholars will also be reviewed in the following section.
- Schiehlen, from the University of Stuttgart, published his two books in 1977 and 1993 respectively. Multibody System Handbook[10] was an international collection of programs and software which included theory research results and programs from 17 research groups. Advanced Multibody Dynamics[11] collected research achievements of the project supported by The German Research Council from 1987 to 1992, and the latest developments in the field of multibody system dynamics worldwide at that time. The content of this book was of an interdisciplinary nature.
- In Computational Methods in Multibody Dynamics[12], Amirouche Farid offered an in-depth analysis of multibody system dynamics with rigid and flexible interconnected bodies, and provided several methods for deriving the equations of motion. Computer methods of tree-like systems and systems with closed loops and prescribed motion were fully discussed.
- In Multi-body Dynamics: Vehicles, machines and mechanisms[13], Rahnejat guided readers through different topics from dynamics principles to the detailed multibody formulation and solution approach. Model analytic solutions were provided for a variety of practical machines and mechanisms such as the suspension of a vehicle and the rotor of helicopter. State-of-the-art modeling and solution methods were presented to investigate complex dynamics phenomena in the behavior of automobiles and aircraft. Optimal control of multibody systems were also discussed.
Multibody dynamics research in China started late but developed quickly. The inaugural meeting of the Multibody System Dynamics group, part of the General Mechanics Committee of Chinese Society of Mechanics, was held in Beijing in August 1986. Since then, many books on multibody system dynamics have come out. Many researchers have published high-quality papers on modeling theory, computational methods, and other subjects of multibody system dynamics[14,15].
1.2.2 Theories and Methods of Multi-Rigid Body System Dynamics
Formulism methods and numerical algorithms are the two most important aspects in multibody system dynamics research. Over the past few decades, many methods have appeared. For example, the New-Euler method by Schiehlen[10], the Kane method by Kane and Huston[2,16], the graph theory method by Roberson and Wittenburg[1,17], and the Lagrangian method by Haug[3] are representative. According to the difference in coordinates adopted, formulism methods can be divided into two categories: minimum number of coordinates method and maximum number of coordinates method. The minimum number of coordinate method uses joint coordinates, taking the relative angular or displacement of the adjacent bodies as generalized coordinates. The main advantage of this method is that fewer variables are used, and higher calculation efficiency can be obtained. However, the construction process of coefficient matrix of differential equations is very complex, including a large amount of nonlinear operations. The maximum number of coordinates method uses the Cartesian coordinates of the center of mass of bodies and the Euler angles or Euler parameters as generalized coordinates, combining Lagrangian multipliers to constraint equations to formulate the equations of motion. This method can be easier implemented for coding, but with the features of more variables and lower calculation efficiency.
- Graph theory (R-W)
Roberson and Witternburg introduced graph theory into the research of multi-rigid body system dynamics. This method applies some basic concepts and mathematical tools to describe the topological structure of a multibody system. The relative displacements of the adjacent bodies are taken as generalized coordinates, and the unified mathematical formula of the complex tree-like structure is derived and the general forms of the dynamic equations are formulated for multibody systems. Code MESA VERDE based on this method has been developed.
- Lagrangian method
This method uses the Cartesian coordinates of the center of mass of bodies and the Euler angles or Euler parameters that describe the orientation of the system as generalized coordinates, combining Lagrangian multipliers to constraint equations to formulate the equations of motion. This method has the characteristic of being easier for programming purposes. Orlandea, Chace, Haug, and Nikravesh developed their general purpose codes ADAMS, DADS, DAP. There are still some differences between them in the detailed formulism and algorithm which is mainly reflected in the different coordinates used. In ADAMS, Cartesian coordinates of the center of mass of bodies and Euler angles that describe the orientation of the system are used as generalized coordinates. In DADS, Cartesian coordinates of the center of mass of bodies and Euler parameters that describe orientation of the system are used as generalized coordinates.
- Multibody dynamics method in ADAMS
For a spatial system with b bodies, the Cartesian coordinates of the center of mass of body i are xi, yi, zi, the Euler angles that describe orientation of the body are ψi, θi, ϕi, the generalized coordinates of the body can be expressed with a vector qi, such as

If vector q is used to denote all of the coordinates of the system, then

If the system contains holonomic and non-holonomic constraints, based on the Lagrangian equations with multipliers, the equations of motion, which are a set of differential–algebraic equations (DAE), can be obtained.
(1.6)
with holonomic constraints equations

and with non-holonomic constraints equations

where, T is the kinetic energy of the system, Q is the vector of generalized forces, ρ is the Lagrange multiplier vector corresponding to holonomic constraints, μ is the Lagrangian multiplier vector corresponding to the non-holonomic constraints.
If the kinetic energy is expressed with velocity and mass, the equations can be written in matrix form.
- Multibody dynamics methods in DADS
For a spatial system with b bodies, the Cartesian coordinates of the center of mass of body i are xi, yi, zi, the Euler parameters that describe the orientation of the body are
 , and the generalized coordinates of the body can be expressed with a vector qi, and
, and the generalized coordinates of the body can be expressed with a vector qi, and  .
.If a vector q is used to denote all of the coordinates of the system, then

For body i, the mass is mi, the inertia matrix in the local coordinate system Ji′ is composed of moments of inertia and products of inertia, the mass characteristics
 , the generalized forces consist of forces and torques acting on body I, such as
, the generalized forces consist of forces and torques acting on body I, such as  , and the angular velocity matrix in local coordinate system is made up by the diagonal matrix
, and the angular velocity matrix in local coordinate system is made up by the diagonal matrix 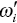 with the entries of angular velocities around the axis.
with the entries of angular velocities around the axis.The constraints equations in compact form
 , with the Jacobian matrix Φq are defined here:
, with the Jacobian matrix Φq are defined here:


The equations of motion can be expressed as:
where λ is the Lagrangian multiplier, and γ is the right side of the acceleration equations.
(1.8)
- Algorithms for solving equations
Normally, the equations of motion of multibody systems are a set of mixed differential-algebraic equations, with the characteristics that their coefficient matrices are quite sparse. There are three main algorithms to solve them: direct integration, coordinate partitioning, and stiff differential equations. The main steps of direct integration are explained below.
To a set of first order differential equations with initial values

Many algorithms can be used to solve them. For example, the Runge-Kutta algorithm, the explicit and implicit multistep algorithm, and the predictor-corrector algorithm are commonly chosen. According to theories of differential equations, n number of ordinary second order differential equations can be expressed as 2n number of first order differential equations:

The matrix form of the equations of motion can also be written as
The following algorithm is adopted to solve the equations:
- Specify the initial conditions of q and
 .
. - Transfer the contents of q and
 into vector
into vector  .
. - Call the numerical integration subroutine to solve the differential equation
 .
.
In the process of numerical integration, f(y, t) must also be calculated. The procedure is outlines as follows:
- Transfer y to q and
 . Assemble the configuration in time.
. Assemble the configuration in time. - At a typical time, calculate M,
 , Q, and γ.
, Q, and γ. - Calculate
 at the typical time.
at the typical time. - Obtain
 and λ by solving equation (1.9).
and λ by solving equation (1.9). - Transfer
 and
and  to y.
to y. - Return.
- Specify the initial conditions of q and
1.2.3 An Example of the Application of Multi-Rigid Body Dynamics Method in Vehicle System Modeling
There are two options for formulating the equations of motion. One is by using existing commercial software; another is using relevant theories whereby researchers do the modeling themselves. The second way will be demonstrated in this chapter. The steps for modeling multi-rigid body systems are basically the same no matter which method is used. These are:
- Simplify practical problems to a system composed of bodies, joints, and force elements.
- Establish the global and local coordinate systems, and determine the generalized coordinates describing the system.
- Calculate the number of degrees of freedom of the system.
- Set up the constraint equations of the system.
- Build the Jacobian matrix, and calculate the right side of the acceleration equation.
- Construct the equations of motion.
The method mentioned above is applied to an automotive electric power steering system.
The diagram of a typical EPS steering system, in this case the type of force assistance on steering column using a rack and pinion mechanical steering mechanism, is shown in Figure 1.1.
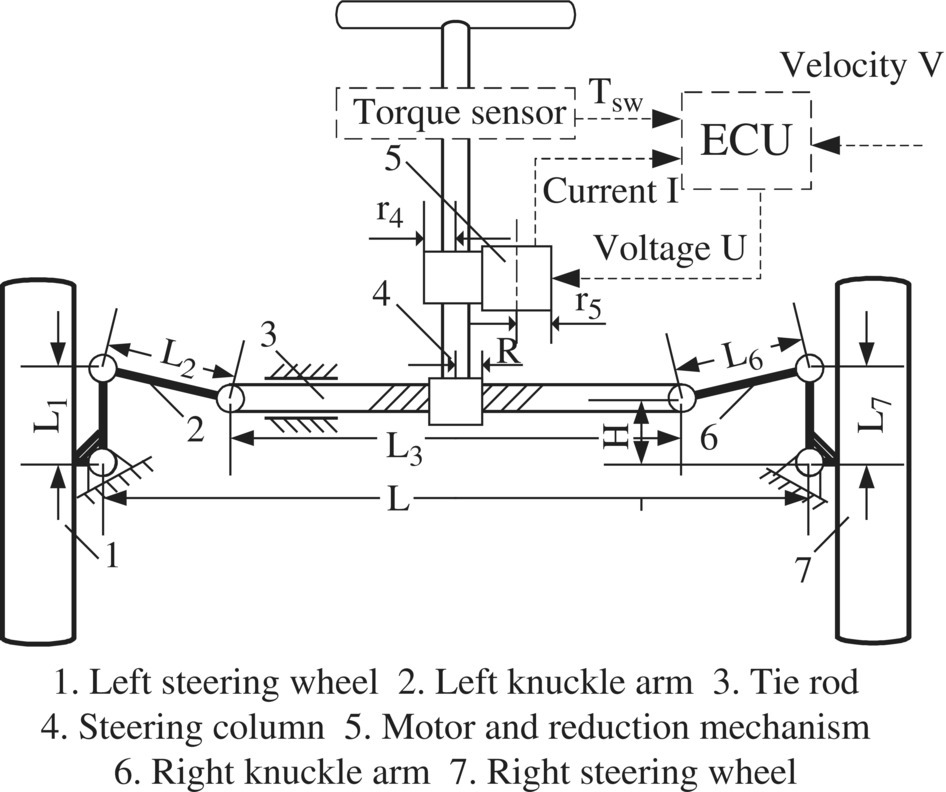
Figure 1.1 Structure of EPS system.
First, the system is simplified. The flexibility of the steering column is neglected, the motor is simplified by reducing the mechanism to a rigid body revolving around a fixed axis. The wheel and the pitman arm are taken as one body. So, as shown in Figure 1.1, the practical system can be treated as a planner multibody system consisting of 7 bodies, 6 revolute joints, 1 translational joint, 1 rack and pinion joint, 1 gear joint, and 2 cylindrical joints. Body 1 and ground, body 2 and body 1, body 2 and body 3 are connected by revolute joints respectively. Body 3 and ground are connected by a translational joint. Body 4 and body 3 are connected by a rack and pinion joint. Body 5 and body 4 are connected by a gear joint. Body 5 and ground are connected by a cylindrical joint. Body 6 and body 3, body 6 and body 7, body 7 and ground are connected by revolute joints respectively. External forces include the steering resistance moment, the input force from the steering wheel, and the assist torque.
The global and local coordinate systems are now established as shown in Figure 1.2. In Cartesian coordinate system, three coordinates are needed to describe the position and orientation of the system. So, the total number of generalized coordinates of the system is 21, which can be expressed as ![]() . The joints provide 20 constraint equations; therefore, the number of degree of freedomn of the system is reduced to 1.
. The joints provide 20 constraint equations; therefore, the number of degree of freedomn of the system is reduced to 1.

Figure 1.2 Plane coordinate system of steering.
The constraint equations of the revolute joints between body 1 and ground, body 2 and body 1, body 2 and body 3 are:
The constraint equations of the translational joints between body 3 and ground are:
The constraint equation of the rack and pinion joint between body 4 and body 3 is:
The constraint equation of the gear joint between body 5 and body 4 is:
The constraint equations of the cylindrical joints between body 4 and ground are:
The constraint equations of the cylindrical joints between body 5 and ground are:
The constraint equations of the revolute joints between body 6 and body 3 are:
The constraint equations of the revolute joints between body 6 and body 7 are:
The constraint equations of the revolute joint between body 7 and ground are:
The Jacobian matrix can be obtained by performing the partial derivative of the items in the 20 equations.

Using the formula ![]() , the right side of the acceleration equation can be calculated. After the moment of inertia, mass matrix, and generalized force vector are determined, the equations of motion can be constructed by applying the formulas (1.7) or (1.9).
, the right side of the acceleration equation can be calculated. After the moment of inertia, mass matrix, and generalized force vector are determined, the equations of motion can be constructed by applying the formulas (1.7) or (1.9).
For more details about equations establishment, literature such as[3],[9],[14], on multibody system dynamics can be consulted.
1.3 Flexible Multibody Dynamics
Flexible multibody dynamics studies the dynamic behavior of systems composed of flexible and rigid multibodies undergoing large-scale spatial motion. The scope of rigid multibody dynamics covers the interaction between the motion of rigid bodies and the influence on dynamic characteristics. The subject of flexible multibody dynamics is the interaction and coupling of flexible bodies’ deformation and overall rigid motion, and the influence on the dynamic behavior of systems. The core feature of flexible multibody system dynamics is that deformation and rigid motion of the object of study occur simultaneously. To flexible bodies, parameters like inertia tensors are functions of time.
Modi[18], Frisch[19] and others have carried out plenty of research in this field. In early 1970s, Bodley et al. established equations using the method of Lagrange multipliers. This theory is quite effective when dealing with flexible multibody systems with constraints, but the derivation process is complicated.
In 1983, NATO-NSF-ARD conducted a seminar on computer-aided analysis and optimization of mechanical systems in which flexible multibody dynamics was one of the important themes. Since the late 1980s, a series of conferences on flexible multibody dynamics have been held in China which have helped to promote the development of the discipline. Most of the studies focused on the dynamics of mechanical systems.
Since 1980s, flexible multibody dynamics have been gradually applied to high-speed flexible mechanisms. Shabana[8], Haug[20] and others have made plenty of contributions in these aspects. Some Chinese researchers applied dynamics analysis to solar energy panels, flexible mechanical arms, and space-borne deployable antennas[21]. The earlier method dealing with the problem of flexible multibody system dynamics was kinematic-elasto dynamics method (KED method). Zhang Ce[22] made the detailed introduction to this method in his book. Using the vector variational method and the principle of virtual work, adopting relative coordinates pulsing modal coordinates of flexible bodies, Hang et al. put forward the modeling method of constrained open-loop, closed-loop mechanical systems and open-loop, closed-loop flexible multibody systems. Chang and Shabana brought forward nonlinear finite element methods for modeling elastic plates undergoing large-scale motion.
Because elastic bodies have an infinite number of degrees of freedom, an accurate solution to these dynamic problems cannot be obtained. The most common approach to handling these problems is to discretize the body to a model with finite degrees of freedom. The main discretization algorithms include: Rayleigh-Litz method, finite element method, modal analysis, and synthesis method.
Mainly, there are three methods for flexible multi-body system dynamics analysis: the Newton Euler method, the Lagrange equation method, and the modification of the two methods, such as the Kane method.
References
- [1] Roberson R E, Schwertassek R. Dynamics of Multibody Systems. Springer-Verlag, Berlin, 1988.
- [2] Kane T R, Likins P W, Levinson D A. Spacecraft Dynamics. McGraw-Hill Book Company, New York, 1983.
- [3] Haug E J. Computer Aided Kinematics and Dynamics of Mechanical Systems. Allyn and Bacon, Boston, 1989.
- [4] Wittenburg J. Dynamics of Systems of Rigid Bodies. B. G. Teubner, Stuttgart, 1977.
- [5] Popov, E.P. Theory of Nonlinear Systems of Automatic Regulation and Control, Nauka, Moscow, 1979.
- [6] Yu Q, Hong J Z. Some topics on flexible multibody system dynamics. Chinese Journal of Advances in Mechanics. 1999, 29(2): 145–154.
- [7] Huang Wen-hu, Chen Bin. The Recent Development of General Mechanics (Dynamics, Vibration and Control). Science Press. Beijing, 1994.
- [8] Shabana A A. Dynamics of Multibody Systems. John Wiley & Sons, New York, 1989.
- [9] Nikravesh P E. Computer-aided Analysis of Mechanical Systems. Prentice Hall, Engelwood Cliffs, NJ, 1988.
- [10] Schiehlen W. Multibody Systems Handbook. Springer-Verlag, Berlin, 1990.
- [11] Schiehlen, W. Advanced Multibody System Dynamics. Kluwer Academic Publishers, Amsterdam, 1992.
- [12] Amirouche F.M.L. Computational Methods in Multibody Dynamics. Prentice Hall, Englewood Cliffs, New Jersey, 1992.
- [13] Rahnejat H. Multi-body Dynamics: Vehicles, Machines and Mechanisms, Professional Engineering Publications (IMechE), 1998.
- [14] Hong Jia-zhen, Jia Shu-Hui. Multibody Dynamics and Control. Beijing Institute of Technology Press, Beijing, 1996.
- [15] Liu Yan-zhu. On dynamics of multibody system described by fully Cartesian coordinates. Chinese Journal of Theoretical and Applied Mechanics, 1997, 29(1): 84–94.
- [16] Huston R L. Multibody Dynamics. Butterworth-Heinemann, Boston, 1990.
- [17] Wittenburg J. Dynamics of Multibody Systems. Springer, Berlin, 2008.
- [18] Modi V J. Attitude dynamics of satellites with flexible appendages: A brief review. J Spacecraft and Rockets, 1974, 11(11): 743–751.
- [19] Frisch H P. A Vector-Dyadic Development of the Equations of Motion for N-Coupled Flexible Bodies and Point Masses. NASA TND-8047, 1975.
- [20] Yoo W S, Haug E J. Dynamics of flexible mechanical systems using vibration and static correction modes. J Mech, Trans and Automation, 1986, 108(3): 315–322.
- [21] Liu Zhu-yong, Hong Jia-zhen. Research and prospect of flexible multi-body systems dynamics. Chinese Journal of Computational Mechanics, 2008, 25(4): 411–416.
- [22] Zhang C. Analysis and Synthesis of Elastic Linkage Mechanism. China Machine Press, Beijing, 1997.


