3.2. Basic Epidemics Models
Epidemics models have attracted the research attention for many years, due to the increased interest for modeling and studying lethal attacks, thus eventually protecting humans from the spreading and propagating of viruses of various types and severity. Multiple times in the past, the human species have suffered severe diseases, such as the black plague that incurred a death toll of around 60% of Europe’s population in the 1300s. Such cases have motivated scientists, mainly mathematicians, to attempt to describe the diffusion dynamics of the outbreaks, in order to be able to respond properly in future occurrences. Furthermore, observations among dependent species in nature, such as foxes-rabbits, for instance, have lead to several models, e.g. predator-prey Lotka-Volterra equations, most of which describe macroscopically the evolution of such ecosystems that have potential interest and importance for humans [99].
The above definition refers to the models developed for the case of biological viruses and their spread in different populations. The term “epidemic” characterizes the cases where the spreading outcome grows fast, yielding significant number of infections, either expected or not. Consequently, the term is used in epidemiology to denote either an emergency state (spreading of a disease has gone beyond control) or a state when a massive spreading is expected (even with less severe outcomes), e.g. flu epidemic every winter.
By analogy, the term epidemics in computer and network science (also sometimes referred to as cyber-attacks or malware) characterizes cases of malicious software diffusing (spreading or propagating) in a given user computer/device population for a given period of time, which usually exceeds substantially what is expected in terms of duration, outcome/impact, or any combination thereof. Thus, epidemics (malware) in computer science follows the interaction between users/machines in a communication network via the underlying infrastructure. Even in biology and epidemiology, epidemics follow an underlying network structure formed by the interacting individuals, e.g. an affiliation human network in the case of the flu spreading. In any case of epidemics, the links of the network formed represent the interactions of the corresponding population through which epidemics diffuse. The term also refers to the models developed in order to describe and study such scenarios.
Standard epidemiological models usually consider homogeneous underlying networks. Homogeneity characterizes network topologies where the degree distribution, typically referred to as connectivity, is classified as homogeneous. Mathematically, this means that the degree distribution peaks at a value, which is the average network degree (denoted by 〈k〉 ), and decays exponentially fast for k≪〈k〉
), and decays exponentially fast for k≪〈k〉 and k≫〈k〉
and k≫〈k〉 , where k
, where k is the degree of a node in the network. Intuitively, this means that the number of neighbors of each network node is relatively “homogeneous” around a central (average) value, and few nodes deviate from this regime. Characteristic example of deterministic homogeneous networks is the standard hypercubic lattice, while among the random homogeneous networks the random graph model of Erdos-Renyi and the Watts-Strogatz (WS) model of small-world (SW) networks. On the other hand, several other networks, most prominently the router network on the Internet or the WWW and DNS networks, have an inhomogeneous structure characterized by power-law degree distributions. Furthermore, network homogeneity refers also to the OS and protocol suites employed, which is the case for most Internet machines that run on one out of a restricted set of available OS/network platforms. Epidemics models have been also developed for such types of complex networks and in the remaining of this chapter, they will be shortly considered and compared against other models. Additional examples for the networks described above may be found in Table 1.2.
is the degree of a node in the network. Intuitively, this means that the number of neighbors of each network node is relatively “homogeneous” around a central (average) value, and few nodes deviate from this regime. Characteristic example of deterministic homogeneous networks is the standard hypercubic lattice, while among the random homogeneous networks the random graph model of Erdos-Renyi and the Watts-Strogatz (WS) model of small-world (SW) networks. On the other hand, several other networks, most prominently the router network on the Internet or the WWW and DNS networks, have an inhomogeneous structure characterized by power-law degree distributions. Furthermore, network homogeneity refers also to the OS and protocol suites employed, which is the case for most Internet machines that run on one out of a restricted set of available OS/network platforms. Epidemics models have been also developed for such types of complex networks and in the remaining of this chapter, they will be shortly considered and compared against other models. Additional examples for the networks described above may be found in Table 1.2.
Among various epidemics models that have been developed in epidemiology to describe the spreading dynamics of viruses for herb, animal, human, and other populations, the most important ones that are suitable for modeling malware diffusion are those denoted as simple epidemic model and the Kermack-McKendrick model. These two basic epidemics models will be analyzed in the following two subsections.
3.2.1. Simple (Classical) Epidemic Model—SI Model
The simple (or sometimes denoted as classical) epidemic model is a straightforward adaptation of epidemics models used extensively in the sciences of biology and ecology [58,99,160]. Traditionally, these models have been used for the study of virus propagations (outbreaks) in closed or interacting living populations, such as the common flu or deadly diseases, e.g. malaria and AIDS in humans, and other viruses in animals, insects, etc.
The main assumption of this approach is that the SI node infection model is considered as the underlying malware propagation model (explained in detail in Section 2.3, Fig. 2.1 and repeated for clarity in Fig. 3.1, which highlights the nature of each state). This is because in the early days of epidemiology, most of these outbreaks, if not all, were lethal, and thus most infected entities would succumb rapidly. A single state transition from the susceptible to the infected state (whichever the outcome of the infected state) was sufficient for an accurate model of the propagation dynamics. The interest of scientists at the time was in estimating the ratio of healthy-to-infected entities as a measure of the infection potential, in order to evaluate the severity of the expected outcome, or predict the potential of a pandemia (state where the infection dominates the population).
Consequently, the purpose of this subsection is to study the simple epidemic model, which is characteristic of the SI malware propagation dynamics. If a piece of malware is identified to follow the SI infection paradigm (or equivalently SI seems to properly describe the infection dynamics of a malware module over a legitimate network), the analytical tools provided in this subsection for studying the SI model can be used directly for analysis of the threat dynamics. In the following, we employ a computer science terminology to describe the analyzed models, i.e. the term “host” or “node” will be used in place of “individual” or “human,” commonly used in epidemiology and biology.
In the simple epidemic model, a total number of hosts N are assumed and the number of susceptible host machines in the system is denoted by S(t)
are assumed and the number of susceptible host machines in the system is denoted by S(t) . Then, since the population is considered closed, the number of currently infected hosts (nodes) at each time is I(t)=N−S(t)
. Then, since the population is considered closed, the number of currently infected hosts (nodes) at each time is I(t)=N−S(t) . We also consider α(t)=I(t)∕N
. We also consider α(t)=I(t)∕N , as the fraction of infected nodes of the attacked network. Another assumption of the model is that of a homogeneous underlying system, namely, each node has the same probability of contacting a malicious (infected/infectious) node and thus become infected. This means the number of contacts between the two distinct node groups is proportional to the product S(t)I(t)
, as the fraction of infected nodes of the attacked network. Another assumption of the model is that of a homogeneous underlying system, namely, each node has the same probability of contacting a malicious (infected/infectious) node and thus become infected. This means the number of contacts between the two distinct node groups is proportional to the product S(t)I(t) . By assuming that β
. By assuming that β represents the attack infection rate, namely, the number of probes sent out by a malware source per time unit, then the homogeneous simple epidemic model (SI infection dynamics) is given by an ODE, which can be formulated in the following alternative forms:
represents the attack infection rate, namely, the number of probes sent out by a malware source per time unit, then the homogeneous simple epidemic model (SI infection dynamics) is given by an ODE, which can be formulated in the following alternative forms:
dI(t)dt=βI(t)S(t)=βI(t)[N−I(t)],
![]() (3.1a)
(3.1a)
dα(t)dt=kα(t)[1−α(t)],
![]() (3.1b)
(3.1b)
dS(t)dt=−βI(t)S(t)=−βS(t)[N−S(t)].
![]() (3.1c)
(3.1c)
In the above set of ODEs, only one of them is independent, since N=S(t)+I(t) and parameter k=βN
and parameter k=βN . Eq. (3.1a) with the initial condition that at t=0
. Eq. (3.1a) with the initial condition that at t=0 , I(0)=I0
, I(0)=I0 hosts are infected and thus S(0)=N−I0
hosts are infected and thus S(0)=N−I0 are noninfected can be solved straightforwardly. The solution of Eq. (3.1a) given the initial condition I(0)=I0
are noninfected can be solved straightforwardly. The solution of Eq. (3.1a) given the initial condition I(0)=I0 is
is
I(t)=I0I0+(1−I0)e−γt,
![]() (3.2)
(3.2)
where β=γN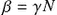 .
.
Eq. (3.1b) is a normalized version of Eq. (3.1a), where α(t)=I(t)∕N is the fraction of the infectious population at time t
is the fraction of the infectious population at time t . Also, Eq. (3.1c) is symmetric with Eq. (3.1a), where I(t)
. Also, Eq. (3.1c) is symmetric with Eq. (3.1a), where I(t) has been replaced with the complementary value N−S(t)
has been replaced with the complementary value N−S(t) , denoting the dependence of S(t)
, denoting the dependence of S(t) , I(t)
, I(t) with respect to N
with respect to N given the considered closed population of the legitimate network. The opposite sign of Eq. (3.1c) is due to the fact that in the SI model, the susceptible population is decreasing, while the infected group is increasing. Both of these trends are evident in the set of alternative equations given in Eqs. (3.1).
given the considered closed population of the legitimate network. The opposite sign of Eq. (3.1c) is due to the fact that in the SI model, the susceptible population is decreasing, while the infected group is increasing. Both of these trends are evident in the set of alternative equations given in Eqs. (3.1).
In general, each of the Eqs. (3.1) constitutes a suitable approximation model for worms and especially for the CodeRed worm [235]. The solution of Eq. (3.1b) is shown in Fig. 3.2, where it is evident that the infection has an exponential growth following a slow-start phase, and finally again leading to a slow-stop phase near the end of the attack. According to the SI dynamics, one expects all hosts to be eventually infected. This is due to the fact that initially, the number of infected nodes is small, and thus the diffusion is restricted. Then, a critical mass of infected nodes is accumulated, in which case the propagation becomes very intense (many malware sources) and the growth of infected nodes becomes exponential. At the final stages, few nodes are still susceptible, and thus any incremental increase to the number of infected nodes shown in Fig. 3.2 becomes very rare, yielding the observed saturation.
Finally, it should be also noted that even though the simple epidemic model is inaccurate for many concurrently spreading pieces of malware, or for some specific types of malware, it is a good first model that may be used to build more elaborate and powerful ones. The epidemics models presented next were set in a broader application perspective and have been developed in order to improve the simple epidemic model for more complex malware behaviors.
3.2.2. General Epidemic Model: Kermack-McKendrick Model
The simple epidemic model can be extended to describe the actual behavior of malware spreading in wired computer networks more accurately, by extending it to the Kermack-McKendrick model [235]. The latter is also denoted as a general epidemic model , and in addition to node infection, it considers the removal of infected nodes. Indeed, in real networks, the infected hosts are not expected to stay in this condition forever, since an end-user will notice sooner or later abnormal behavior of the infected device and will act on that. Thus, in addition to the previous simple epidemic model, some of the nodes are removed completely from the network.
Similarly to the simple epidemic model corresponding to the SI infection paradigm, the general (Kermack-McKendrick) epidemic model corresponds to the SIR infection paradigm, as shown in Fig. 2.1 and repeated in Fig. 3.3, highlighting further the considered states of legitimate nodes. The state R is denoted as “removed” and typically represents cases that nodes are either completely damaged (e.g. run out of battery or other resources) by the attack, or eventually recover and they are permanently immunized by the specific malware type. In the latter case, the SIS model would also seem appropriate. However, the SIS paradigm is more accurate for the cases of modeling a system in the long-term (for an extensive period of time, or if the analysis considered multiple possible threats spreading/propagating, where in both cases infections and the susceptible state are recurrent). The SIR paradigm, and thus the Kermack-McKendrick model as well, has been developed for the study of specific malware threats, each potentially diffusing individually across the network. Consequently, if a node recovers from such infection, it will be concurrently patched and protected from future contacts with attack nodes and their malware. Equivalently, if a node becomes completely dysfunctional from the received infection, it will not be able to come in contact with attackers or other legitimate nodes in the future. Thus, the SIR mapping to the Kermack-McKendrick model is more appropriate and the two terms (SIR, Kermack-McKendrick model) will be used interchangeably in the rest of this book when we refer to practical application of SIR epidemics models.
Based on the set of simple epidemics dynamics given in Eqs. (3.1), the general epidemic model (SIR paradigm) dynamics can be obtained by taking into account the node removal process. The Kermack-McKendrick model dynamics are given by the following system of ODEs:
dS(t)dt=−βS(t)I(t)N,
![]() (3.3a)
(3.3a)
dI(t)dt=βS(t)I(t)N−γI(t),
![]() (3.3b)
(3.3b)
dR(t)dt=γI(t),
![]() (3.3c)
(3.3c)
N=S(t)+I(t)+R(t),
![]() (3.3d)
(3.3d)
which can be also cast in an alternative form
dJ(t)dt=βJ(t)[N−J(t)],
![]() (3.4a)
(3.4a)
dR(t)dt=γI(t),
![]() (3.4b)
(3.4b)
J(t)=I(t)+R(t)=N−S(t),
![]()
where β is the infection rate, γ
is the infection rate, γ is the rate of removal of infectious hosts from the malware circulation process, and S(t)
is the rate of removal of infectious hosts from the malware circulation process, and S(t) , I(t)
, I(t) , and R(t)
, and R(t) are the number of susceptible, infected, and removed nodes at time t
are the number of susceptible, infected, and removed nodes at time t , respectively. Parameter N
, respectively. Parameter N is the total size of the population as in the simple epidemic model. J(t)
is the total size of the population as in the simple epidemic model. J(t) is the equivalent of infected nodes in the simple epidemic model. Just as the group of susceptible nodes reduces and the coupled group of infected increases by the same amount in the simple epidemic model, in the general epidemic model, the groups S(t)
is the equivalent of infected nodes in the simple epidemic model. Just as the group of susceptible nodes reduces and the coupled group of infected increases by the same amount in the simple epidemic model, in the general epidemic model, the groups S(t) , J(t)
, J(t) are coupled in the general epidemic model, and thus the simple epidemic model Eq. (3.1a) can be used for modeling the general epidemics behavior where now the term I(t)
are coupled in the general epidemic model, and thus the simple epidemic model Eq. (3.1a) can be used for modeling the general epidemics behavior where now the term I(t) in the simple epidemic should be replaced by the equivalent J(t)
in the simple epidemic should be replaced by the equivalent J(t) in the general epidemic. Also, a new equation for the removal rate (Eq. (3.4b)) was included. Together with the initial conditions I(0)
in the general epidemic. Also, a new equation for the removal rate (Eq. (3.4b)) was included. Together with the initial conditions I(0) and R(0)
and R(0) , the problem is fully determined via the system of Eqs. (3.4).
, the problem is fully determined via the system of Eqs. (3.4).
One of the most characteristic features of the Kermack-McKendrick model, derived from the solution of Eqs. (3.4), is the emergence of the infamous epidemic threshold. The epidemic threshold advocates that a major outbreak occurs if and only if the initial number of susceptible hosts S(0)>ρ , where ρ=γ∕β
, where ρ=γ∕β . Thus, ρ
. Thus, ρ is called the epidemic threshold. The epidemic threshold quantifies the number of secondary infections caused by a single primary infection. In other words, it determines the number of users infected by contact with a single infected user machine before the death or recovery of the latter.
is called the epidemic threshold. The epidemic threshold quantifies the number of secondary infections caused by a single primary infection. In other words, it determines the number of users infected by contact with a single infected user machine before the death or recovery of the latter.
Furthermore, it can be derived from the system of Eqs. (3.4) that dI(t)∕dt<0 if and only if S(0)<ρ
if and only if S(0)<ρ . The emergence of the epidemic threshold is an instance of threshold phenomena, which can be observed in many complex network processes, e.g. percolation [35,64,89]. Another similar and very prominent threshold behavior in some types of wireless complex networks is connectivity and the emergence of a giant cluster of nodes in the network as the transmission radius or network density increases. Such networks are modeled as random geometric graphs and their connectivity exhibits threshold behavior with respect to the scaling of their transmission range radius and their deployment region [180].
. The emergence of the epidemic threshold is an instance of threshold phenomena, which can be observed in many complex network processes, e.g. percolation [35,64,89]. Another similar and very prominent threshold behavior in some types of wireless complex networks is connectivity and the emergence of a giant cluster of nodes in the network as the transmission radius or network density increases. Such networks are modeled as random geometric graphs and their connectivity exhibits threshold behavior with respect to the scaling of their transmission range radius and their deployment region [180].
3.2.3. Two-factor Model
The previous epidemics models do not take into account the case where an infection of a susceptible node is rapidly detected and the specific node is directly quarantined (i.e. removed from the network, or at least prohibited from communicating with other host machines) from the user or network administrator, in order to prevent it from further propagating the received malware. This is a similar behavior to the one observed in human viruses, e.g. the common flu, where once a person becomes infected she/he is put in a form of isolation avoiding excessive interaction (or even avoiding completely interaction with others) to prevent transmission to other persons, proactively or mandatorily [58].
A basic assumption in the previous epidemics models is that malware and more specifically worms as the ones modeled by the simple and general epidemic models continuously search for available susceptible nodes to infect. However, in reality, worms usually do not continuously spread forever. For instance, the CodeRed worm stopped propagation at 00:00 UTC July 20th, 2001 [235].
In general, one can observe two specific aspects of worm propagation, not taken into account by the simple and Kermack-McKendrick epidemic models:
1. Human countermeasures result in removing both susceptible and infectious computers from circulation. This corresponds to users becoming more aware of the spreading threats and either take some precautions while susceptible, or act rapidly once infected.
2. The infection rate is usually decreasing with time, i.e. β=β(t) is a decreasing function rather than constant. This could model, for example, the effect of a vast worm attack, where Internet routers become bottlenecked and thus the worm scanning process is slowed down.
is a decreasing function rather than constant. This could model, for example, the effect of a vast worm attack, where Internet routers become bottlenecked and thus the worm scanning process is slowed down.
Both of these observations have been actually observed in the behavior of CodeRed worm spreading [235]. The cumulative effect of these two observations is a time-dependent and decreasing worm infection rate. From the worm’s perspective, human countermeasures remove some hosts from worm spreading circulation, including both hosts that are infectious and hosts that are still susceptible. In other words, the removal process consists of two parts: removal of infectious hosts I(t) and removal of susceptible hosts S(t)
and removal of susceptible hosts S(t) . Thus, the more suitable infection paradigm model in this case is an extended SIR one, where the removed hosts come both from S,I
. Thus, the more suitable infection paradigm model in this case is an extended SIR one, where the removed hosts come both from S,I populations. The removed susceptible users are denoted by Q(t)
populations. The removed susceptible users are denoted by Q(t) and referred to as quarantined, since they are usually informed users that take proper precautions. The removed infected nodes are simply referred to as removed and denoted by R(t)
and referred to as quarantined, since they are usually informed users that take proper precautions. The removed infected nodes are simply referred to as removed and denoted by R(t) . The involved user groups, S(t),I(t),Q(t)
. The involved user groups, S(t),I(t),Q(t) , and R(t)
, and R(t) , are shown in Fig. 3.4 and they are identical to the dynamic quarantine model assumed states that will be explained in the next subsection. It should be noted that the category Q(t)
, are shown in Fig. 3.4 and they are identical to the dynamic quarantine model assumed states that will be explained in the next subsection. It should be noted that the category Q(t) of susceptible nodes was not introduced in Chapter 2; however, a realistic consideration of malware epidemics calls for such a possible state for susceptible nodes.
of susceptible nodes was not introduced in Chapter 2; however, a realistic consideration of malware epidemics calls for such a possible state for susceptible nodes.
The change in the number of susceptible hosts S(t) from time t
from time t to time t+Δt
to time t+Δt is given by
is given by
S(t+Δt)−S(t)=−β(t)S(t)I(t)Δt−dQ(t)dtΔt.
![]() (3.5)
(3.5)
Consequently, the basic epidemics equation now becomes
dS(t)dt=−β(t)S(t)I(t)−dQ(t)dt,
![]() (3.6)
(3.6)
where now S(t)+I(t)+R(t)+Q(t)=N at any time t
at any time t . Thus, the epidemics equation of the two-factor model (which extends the corresponding equation of the SIR model with the two observations mentioned above) becomes
. Thus, the epidemics equation of the two-factor model (which extends the corresponding equation of the SIR model with the two observations mentioned above) becomes
dI(t)dt=β(t)[N−R(t)−I(t)−Q(t)]I(t)−dR(t)dt.
![]() (3.7)
(3.7)
In order to solve Eq. (3.7), one needs to know the dynamic properties of β(t) , R(t)
, R(t) , and Q(t)
, and Q(t) . Parameter β(t)
. Parameter β(t) is determined by the impact of worm traffic on Internet infrastructure, and the spreading efficiency of the worm code. Parameters R(t)
is determined by the impact of worm traffic on Internet infrastructure, and the spreading efficiency of the worm code. Parameters R(t) and Q(t)
and Q(t) involve any awareness that users/administrators might have of the worm, or any patching and filtering difficulties. By specifying their dynamic properties, the complete set of differential equations of the two-factor worm model can be obtained.
involve any awareness that users/administrators might have of the worm, or any patching and filtering difficulties. By specifying their dynamic properties, the complete set of differential equations of the two-factor worm model can be obtained.
To date, obtaining directly the general two-factor worm model in analytical closed-form solutions was not possible. Instead, one may use a numerical model, in which she/he needs to determine the dynamical equations describing R(t) , Q(t)
, Q(t) , and β(t)
, and β(t) in the model described by Eq. (3.7). For the removal process from infectious hosts, the same assumption as in the Kermack-McKendrick model can be assumed, namely, dR(t)∕dt=γI(t)
in the model described by Eq. (3.7). For the removal process from infectious hosts, the same assumption as in the Kermack-McKendrick model can be assumed, namely, dR(t)∕dt=γI(t) . The removal process from the set of susceptible hosts is more complicated. At the beginning of the worm propagation, most people do not know there exists such a kind of worm. Consequently, the number of removed susceptible hosts is small and increases slowly. As more systems become infected, awareness increases. Hence, the speed of immunization (quarantining) increases fast as time passes. The speed decreases as the number of susceptible hosts shrinks and converges to zero when there are no susceptible hosts available. The classical simple epidemic equation can be employed to model such behavior dQ(t)∕dt=μS(t)I(t)
. The removal process from the set of susceptible hosts is more complicated. At the beginning of the worm propagation, most people do not know there exists such a kind of worm. Consequently, the number of removed susceptible hosts is small and increases slowly. As more systems become infected, awareness increases. Hence, the speed of immunization (quarantining) increases fast as time passes. The speed decreases as the number of susceptible hosts shrinks and converges to zero when there are no susceptible hosts available. The classical simple epidemic equation can be employed to model such behavior dQ(t)∕dt=μS(t)I(t) . The decreased infection rate can be described as
. The decreased infection rate can be described as
β(t)=β0[1−I(t)N]n,
 (3.8)
(3.8)
where β0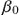 is the initial infection rate. The exponent n
is the initial infection rate. The exponent n is used to adjust the infection rate sensitivity to the number of infectious hosts, where n=0
is used to adjust the infection rate sensitivity to the number of infectious hosts, where n=0 corresponds to a constant infection rate. Using the assumptions above on Q(t)
corresponds to a constant infection rate. Using the assumptions above on Q(t) , R(t)
, R(t) , and β(t)
, and β(t) , the complete differential equations of the two-factor worm model are
, the complete differential equations of the two-factor worm model are
dS(t)dt=−β(t)S(t)I(t)−dQ(t)dt,
![]() (3.9a)
(3.9a)
dR(t)dt=γI(t),
![]() (3.9b)
(3.9b)
dQ(t)dt=μS(t)I(t),
![]() (3.9c)
(3.9c)
β(t)=β0[1−I(t)N]n,
 (3.9d)
(3.9d)
N=S(t)+I(t)+R(t)+Q(t),
![]() (3.9e)
(3.9e)
I(0)=I0≪N;S(0)=N−I0;R(0)=Q(0)=0.
![]() (3.9f)
(3.9f)
It can be derived that dI(t)∕dt=β(t)S(t)I(t)−dR(t)∕dt=[β(t)S(t)−γ]I(t) , and the number of susceptible hosts S(t)
, and the number of susceptible hosts S(t) is a monotonically decreasing function of time. The maximum number of infectious hosts will be reached at time tc
is a monotonically decreasing function of time. The maximum number of infectious hosts will be reached at time tc when S(tc)=γ∕β(tc)
when S(tc)=γ∕β(tc) . At the same time, β(t)S(t)−γ<0
. At the same time, β(t)S(t)−γ<0 for t>tc
for t>tc ; thus, I(t)
; thus, I(t) decreases after t>tc
decreases after t>tc .
.
Fig. 3.5 demonstrates the number of infected and removed hosts as a function of time. The susceptible removed hosts Q(t) are also depicted for comparison purposes. It also compares with the infected nodes value predicted by the simple epidemic model.
are also depicted for comparison purposes. It also compares with the infected nodes value predicted by the simple epidemic model.
3.2.4. Dynamic Quarantine
Similarly to the two-factor model, the dynamic quarantine model has been developed to take into account cases where a worm infection is rapidly detected and some of the infected machines are quarantined to prevent them from further propagating the received malware [234]. The quarantined node can be considered as a form of removed node from the network, and as shown in Fig. 3.4, these nodes are not further considered in the malware propagation process, similarly to the two-factor propagation model.
With respect to epidemics control in the real world, people usually react under the principle that whenever a person exhibits a symptom slightly similar to an expected one for a disease, he or she will be quarantined immediately. The quarantine will be released after the person passes the disease latent period without showing up further symptoms. This is referred to as the “assume guilty before proven innocent” rule of thumb.
In terms of worm propagation, such a soft quarantine strategy will allow that every host of the system can be quarantined individually when the worm anomaly detection program raises alarm for some host. The quarantine on a host under alarm is released after a quarantine time T , even if the host has not been inspected by the user or an administrator yet. Once the quarantine on a host is released, this host can be quarantined again if the anomaly detection program raises an alarm for this host some time later. The specific means of quarantine may vary considerably, from simple traffic filtering/blocking based packet sniffing and port filtering according to identified malware traffic signatures to more sophisticated ones where constant monitoring of traffic and information exchange is required. All these countermeasures depend on the availability of the specific infrastructure and associated resources.
, even if the host has not been inspected by the user or an administrator yet. Once the quarantine on a host is released, this host can be quarantined again if the anomaly detection program raises an alarm for this host some time later. The specific means of quarantine may vary considerably, from simple traffic filtering/blocking based packet sniffing and port filtering according to identified malware traffic signatures to more sophisticated ones where constant monitoring of traffic and information exchange is required. All these countermeasures depend on the availability of the specific infrastructure and associated resources.
The dynamic quarantine method has two advantages: first, a falsely quarantined but otherwise healthy host will only be quarantined for a short time; thus, its normal activities will not be impacted too much. Second, since in this case a higher false alarm rate than the normal permanent quarantine can be tolerated, the worm anomaly detection program can be set more sensitive to a worm’s activities.
The simplest such quarantine approach considers constant quarantine time and the anomaly detection threshold throughout the spreading period of a worm. On average, an infectious host will be detected in 1∕λ1 units of time after the host becomes infectious, or after it is released from a previous quarantine. The total time corresponds to the propagation time of an infectious host before having been discovered and quarantined. Parameter λ1
units of time after the host becomes infectious, or after it is released from a previous quarantine. The total time corresponds to the propagation time of an infectious host before having been discovered and quarantined. Parameter λ1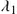 is denoted as the quarantine rate of infectious hosts. A healthy, nonquarantined host will keep its normal activities for 1∕λ2
is denoted as the quarantine rate of infectious hosts. A healthy, nonquarantined host will keep its normal activities for 1∕λ2 units of time on average before it is falsely alarmed and quarantined. Thus, λ2
units of time on average before it is falsely alarmed and quarantined. Thus, λ2 is the quarantine rate of susceptible hosts and corresponds to the false alarm rate of the anomaly detection program used in the system. The values of λ1
is the quarantine rate of susceptible hosts and corresponds to the false alarm rate of the anomaly detection program used in the system. The values of λ1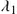 and λ2
and λ2 are determined both by the threshold and by the performance (and sensitivity) of the anomaly detection program employed. A high performance anomaly detection program has higher detection rate and lower false alarm rate, i.e. the detection program has larger λ1
are determined both by the threshold and by the performance (and sensitivity) of the anomaly detection program employed. A high performance anomaly detection program has higher detection rate and lower false alarm rate, i.e. the detection program has larger λ1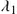 and smaller λ2
and smaller λ2 than a worm detection program with ordinary performance.
than a worm detection program with ordinary performance.
Based on the above notation, we obtain the number of infectious hosts removed as
R(t)=∫tt−T[I(τ)−R(τ)]λ1dτ,
 (3.10)
(3.10)
which is correct only for large populations, due to the use of the average value λ1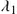 . To grasp this better, one should keep in mind that in large populations, a great number of interactions are expected to take place. Furthermore, these interactions tend to be more “random” than in smaller populations, since within the large population multiplexing between different behaviors is expected. In other words, the large population is expected to mix better than a small population, in which case, average values are quite representative for all users. In the following, we will study how the dynamic quarantine affects a worm’s propagation by extending the simple epidemic model and the Kermack-McKendrick model, respectively.
. To grasp this better, one should keep in mind that in large populations, a great number of interactions are expected to take place. Furthermore, these interactions tend to be more “random” than in smaller populations, since within the large population multiplexing between different behaviors is expected. In other words, the large population is expected to mix better than a small population, in which case, average values are quite representative for all users. In the following, we will study how the dynamic quarantine affects a worm’s propagation by extending the simple epidemic model and the Kermack-McKendrick model, respectively.
For the simple epidemic model, a host is either susceptible or infectious. Due to the dynamic quarantine, a host is also either quarantined or not quarantined at any time t . Based on the state dynamics shown in Fig. 3.4, the interactions of the simple epidemics dynamics are now between [I(t)−R(t)]
. Based on the state dynamics shown in Fig. 3.4, the interactions of the simple epidemics dynamics are now between [I(t)−R(t)] and [S(t)−Q(t)]
and [S(t)−Q(t)] . Therefore, the dynamics of simple epidemic model under dynamic quarantine now follows
. Therefore, the dynamics of simple epidemic model under dynamic quarantine now follows
dI(t)dt=β[I(t)−R(t)][S(t)−Q(t)]=β′,I(t)[N−I(t)],
![]() (3.11)
(3.11)
where β′=(1−p′1)(1−p′2)β is the effective pairwise rate of infection, i.e. the actual rate of infection that would be observed between a randomly selected pair of nodes, p′1=λ1T1+λ1T
is the effective pairwise rate of infection, i.e. the actual rate of infection that would be observed between a randomly selected pair of nodes, p′1=λ1T1+λ1T is the effective quarantine probability of infectious hosts, p′2=λ2T1+λ2T
is the effective quarantine probability of infectious hosts, p′2=λ2T1+λ2T the effective quarantine probability of susceptible hosts, and T
the effective quarantine probability of susceptible hosts, and T the observation time interval. It should be also noted that Q(t)=p′2S(t)
the observation time interval. It should be also noted that Q(t)=p′2S(t) .
.
The above equation shows that under dynamic quarantine, a worm still propagates according to simple epidemic model but with slower spreading speed. The dynamic quarantine decreases a worm’s pairwise rate of infection β by the factor of (1−p′1)(1−p′2)
by the factor of (1−p′1)(1−p′2) : the larger the effective quarantine probabilities p′1
: the larger the effective quarantine probabilities p′1 and p′2
and p′2 are, the slower the worm can propagate [234]. Therefore, when one implements the dynamic quarantine, it can provide precious time to take counteractions—patching vulnerable computers and cleaning infected ones—before a worm infects the major part of a network.
are, the slower the worm can propagate [234]. Therefore, when one implements the dynamic quarantine, it can provide precious time to take counteractions—patching vulnerable computers and cleaning infected ones—before a worm infects the major part of a network.
Shifting back to the case of the Kermack-McKendrick model, assume that U(t) denotes the number of removed hosts from infectious only. Then, it follows dU(t)∕dt=γI(t)
denotes the number of removed hosts from infectious only. Then, it follows dU(t)∕dt=γI(t) . Removal of the infectious hosts takes place uniformly from the set of infected nodes I(t)
. Removal of the infectious hosts takes place uniformly from the set of infected nodes I(t) , which could also include nodes that are under quarantine when they are selected for removal. Assume that before removal R(t)=p′1I(t)
, which could also include nodes that are under quarantine when they are selected for removal. Assume that before removal R(t)=p′1I(t) and Q(t)=p′2S(t)
and Q(t)=p′2S(t) . When the removal process is in effect, Q(t)=p′2S(t)
. When the removal process is in effect, Q(t)=p′2S(t) still holds. However, Eq. (3.10) should be modified to consider the removed hosts from R(t)
still holds. However, Eq. (3.10) should be modified to consider the removed hosts from R(t) during time [(t−T),t]
during time [(t−T),t] . Since the removal process uniformly removes infectious hosts from I(t)
. Since the removal process uniformly removes infectious hosts from I(t) , the removal rate from quarantined R(t)
, the removal rate from quarantined R(t) (quarantined infected hosts) should be γR(t)
(quarantined infected hosts) should be γR(t) at time t
at time t . Therefore, Eq. (3.10) can be extended to
. Therefore, Eq. (3.10) can be extended to
R(t)=∫tt−T[I(τ)−R(τ)]λ1dτ−∫tt−TγR(τ)dτ.
 (3.12)
(3.12)
With the assumption that R(τ)≅R(t) and I(τ)≅I(t)
and I(τ)≅I(t) , ∀τ∈[t−T,t]
, ∀τ∈[t−T,t] , it is obtained R(t)=q′1I(t)
, it is obtained R(t)=q′1I(t) , where q′1=λ1T1+(λ1+γ)T
, where q′1=λ1T1+(λ1+γ)T is the effective quarantine probability of infectious hosts for a worm’s propagation with removal process. It should be noted that such an assumption holds when the quarantine time T
is the effective quarantine probability of infectious hosts for a worm’s propagation with removal process. It should be noted that such an assumption holds when the quarantine time T is small, compared with the model’s dynamics (time scale that changes happen in the network). Some relevant discussion and more details are contained at the end of this subsection. For consistency, q′2=p′2=λ2T1+(λ2+γ)T
is small, compared with the model’s dynamics (time scale that changes happen in the network). Some relevant discussion and more details are contained at the end of this subsection. For consistency, q′2=p′2=λ2T1+(λ2+γ)T as the effective quarantine probability of susceptible hosts for a worm’s propagation with removal process.
as the effective quarantine probability of susceptible hosts for a worm’s propagation with removal process.
The propagation dynamics will be now governed by
dI(t)∕dt=β[I(t)−R(t)][S(t)−Q(t)]−γI(t)=β″
![]() (3.13)
(3.13)
where  is the effective pairwise rate of infection for a worm’s propagation with removal process. The worm propagation model given by Eq. (3.13) is the same as the Kermack-McKendrick model, except that the pairwise rate of infection
is the effective pairwise rate of infection for a worm’s propagation with removal process. The worm propagation model given by Eq. (3.13) is the same as the Kermack-McKendrick model, except that the pairwise rate of infection  is decreased from
is decreased from  by the factor of
by the factor of  . The new dynamic quarantine system will have an epidemic threshold
. The new dynamic quarantine system will have an epidemic threshold  that is
that is
 (3.14)
(3.14)
If the initial number of susceptible hosts  satisfies the relationships
satisfies the relationships  and
and  , then according to the Kermack-McKendrick epidemic threshold theorem, a worm will spread out in the original system but will not be able to spread out when we implement dynamic quarantine on the system. In other words, the dynamic quarantine method reduces the chance for a worm to form an outbreak, i.e. a holistic spread of the worm in the whole network (case of pandemia).
, then according to the Kermack-McKendrick epidemic threshold theorem, a worm will spread out in the original system but will not be able to spread out when we implement dynamic quarantine on the system. In other words, the dynamic quarantine method reduces the chance for a worm to form an outbreak, i.e. a holistic spread of the worm in the whole network (case of pandemia).
In the previous model, all infectious hosts have an equal probability to be removed. However, a more realistic scenario is that some authority inspects the hosts that have raised alarm and have been quarantined. This is justified since limited human resources do not permit the full-scale inspection of all hosts, while alarmed hosts are more likely to be infected by a worm. Therefore, in such a dynamic quarantine system, only infectious hosts in the quarantined population (the latter denoted now by  ) could be removed. In this case, the number of removed hosts from quarantined infectious population
) could be removed. In this case, the number of removed hosts from quarantined infectious population  (denoted by
(denoted by  ) follows
) follows  . Eq. (3.12) remains valid and the propagation dynamics become
. Eq. (3.12) remains valid and the propagation dynamics become
![]() (3.15)
(3.15)
where  is the effective removal rate. This model has the same form as the Kermack-McKendrick; therefore, all outcomes regarding the Kermack-McKendrick model remain valid. The epidemic threshold becomes
is the effective removal rate. This model has the same form as the Kermack-McKendrick; therefore, all outcomes regarding the Kermack-McKendrick model remain valid. The epidemic threshold becomes
 (3.16)
(3.16)
where  as denoted above. The epidemic threshold theorem states that if
as denoted above. The epidemic threshold theorem states that if  , a worm will not form an outbreak in this dynamic quarantine system.
, a worm will not form an outbreak in this dynamic quarantine system.
On a final note, it should be stated that all the previous analyses are based on two assumptions. First, the quarantine time T is small such that
 (3.17)
(3.17)
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.





