Appendix A
Systems of ordinary differential equations
Abstract
This appendix serves the purpose of a brief introduction to ordinary differential equations and systems thereof. A concise and nonexhaustive collection of methods and techniques used to find solutions to several types of differential equations, including first-order scalar equations, second order linear equations, and systems of linear equations, is included. In most cases, the reader is directed to more thorough and complete treatises, while this appendix offers a brief idea of the background material required for better understanding the mathematical models and methodologies employed in the analysis of malware diffusion in computer and communications networks, especially those based on epidemics models.
A.1. Initial Definitions
A differential equation is an equation that contains one or more derivatives of an unknown function. Differential equations are extensively used in mathematical modeling of many systems. When the independent variable is time, then the differential equation describes the temporal dynamics of a monolithic quantity, e.g. population, capital investment, chemical compound, decayed radioactive material, and so on. Other independent random variables such as the spatial coordinates can give more detailed description of a spatiotemporal quantity with spatiotemporal dynamics, e.g. diffusion of heat and fluids. In the rest of this appendix, we assume that the independent variable is time and denote it by  . Any other interpretation of
. Any other interpretation of  is valid too.
is valid too.
A differential equation that only contains ordinary derivatives is called an ODE. If, on the other hand, one or more partial derivatives are involved as well, it is referred to as a partial differential equations (PDEs) [81]. Each of these two broad categories is further classified based on the highest order of derivative that appears in them. In this appendix, we only consider ODEs.
Depending on the number of unknown functions that are involved, a classification to single ODE and system of ODEs is obtained. If there is a single function to be determined, then one equation is sufficient. However, if there are two or more unknown functions, then a system of equations is required.
Let  in a space
in a space  (for some proper dimension
(for some proper dimension  of the space) be a function of a single-dimensional real-valued variable
of the space) be a function of a single-dimensional real-valued variable  . Furthermore, for any positive integer
. Furthermore, for any positive integer  , let
, let  represent the
represent the  th order derivative of
th order derivative of  with respect to
with respect to  evaluated at
evaluated at  , i.e.
, i.e.  evaluated at
evaluated at  . Then, we have the following.
. Then, we have the following.
In the rest of this appendix, whenever not ambiguous, we will suppress the explicit dependence on  for simplicity of notation. Note that the first and second order derivatives are also often denoted by
for simplicity of notation. Note that the first and second order derivatives are also often denoted by  and
and  , and specially when the independent variable is time, also by
, and specially when the independent variable is time, also by  and
and  as well.
as well.
ODE (A.1) is said to be linear if  is a linear function of the variables
is a linear function of the variables  . A similar definition applies to PDEs. An equation not in linear form is called nonlinear ODE or PDE, respectively.
. A similar definition applies to PDEs. An equation not in linear form is called nonlinear ODE or PDE, respectively.
An important class of first-order equations are those in which the independent variable does not appear explicitly. Such equations are called autonomous and have the form  .
.
This definition describes an exact solution of the ODE, as opposed to an approximate one. When a solution of the ODE needs to satisfy the initial condition of  for a given
for a given  , we refer to the problem as an initial value problem (IVP). Some very important questions about a solution of an ODE (PDE) or an IVP is the existence, uniqueness, and stability of solution or solutions.
, we refer to the problem as an initial value problem (IVP). Some very important questions about a solution of an ODE (PDE) or an IVP is the existence, uniqueness, and stability of solution or solutions.
A.2. First-order Differential Equations
By Eq. (A.1) and when  is invertible with respect to
is invertible with respect to  , a first-order ODE may also be expressed in the following form:
, a first-order ODE may also be expressed in the following form:
![]() (A.2)
(A.2)
for a function  . For linear first-order ODEs, the integrating factor solution approach can be used to obtain the desired result. Details on the application of such techniques can be found in [40, Section 2.1].
. For linear first-order ODEs, the integrating factor solution approach can be used to obtain the desired result. Details on the application of such techniques can be found in [40, Section 2.1].
In cases where  is a single-valued function of
is a single-valued function of  , this is just a single ODE. If, on the other hand,
, this is just a single ODE. If, on the other hand,  is a multivalued function of
is a multivalued function of  , i.e.
, i.e.  for a positive integer
for a positive integer  , then the ODE can be decomposed and expressed in terms of each element of the vector function
, then the ODE can be decomposed and expressed in terms of each element of the vector function  . For such a case, the
. For such a case, the  function is also multivalued, i.e.
function is also multivalued, i.e.  such that each
such that each  . This leads to the following system of
. This leads to the following system of  differential equations:
differential equations:
![]() (A.3)
(A.3)
that need to be simultaneously satisfied over the interval of solution. The converse direction yields another interpretation of the above system of first-order ODEs. According to this if there are  unknown functions
unknown functions  that need to simultaneously satisfy
that need to simultaneously satisfy  first-order differential equations, then by introducing an
first-order differential equations, then by introducing an  -dimensional vector-valued function one may obtain a single vectorized differential equation.
-dimensional vector-valued function one may obtain a single vectorized differential equation.
The form of first-order ODE presented in (A.2) can also model higher order ODEs through introduction of auxiliary dependent variables. Specifically, consider an  -th order ODE of the form
-th order ODE of the form  . Now consider the auxiliary functions
. Now consider the auxiliary functions  such that
such that  ,
,  ,
,  , and so on till
, and so on till  . Then, we have
. Then, we have 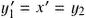 ,
,  . Moreover,
. Moreover,  , which must be equal to
, which must be equal to  , hence
, hence  . Hence, the
. Hence, the  th order ODE
th order ODE  is equivalent to the following system of ODEs:
is equivalent to the following system of ODEs:
![]()
![]()
 (A.4)
(A.4)
where  ,
,  are real-valued continuous functions of
are real-valued continuous functions of  over the interval
over the interval  , then we have a first-order system of linear ODEs. Using the technique of introducing auxiliary functions for higher order derivatives of the unknown function
, then we have a first-order system of linear ODEs. Using the technique of introducing auxiliary functions for higher order derivatives of the unknown function  , we can convert the
, we can convert the  -th order linear ODE of
-th order linear ODE of  into a first-order system of linear ODEs too [40]. The analysis and properties of (systems of) linear ODEs are well-developed, and consequently, whenever meaningful, nonlinear ODE systems are analyzed by approximating them through “linearization” (around an operation point) [40].
into a first-order system of linear ODEs too [40]. The analysis and properties of (systems of) linear ODEs are well-developed, and consequently, whenever meaningful, nonlinear ODE systems are analyzed by approximating them through “linearization” (around an operation point) [40].
Some first-order ODEs of the form  can be transformed as
can be transformed as  and cast in the form
and cast in the form  when
when  is a function of
is a function of  and
and  a function of
a function of  . Such equations are called separable. The solution to such equation can be easily obtained. More on separable ODEs and their solution methodology can be found in [40].
. Such equations are called separable. The solution to such equation can be easily obtained. More on separable ODEs and their solution methodology can be found in [40].
A.3. Existence and Uniqueness of a Solution
Existence of a solution to any ODE of the form  with initial condition
with initial condition  is guaranteed for any continuous finite dimensional function
is guaranteed for any continuous finite dimensional function  . More formally, we have the following.
. More formally, we have the following.
In (A.2), we say function  satisfies a
satisfies a  -Lipschitz condition in
-Lipschitz condition in  over
over  , where
, where  , if there exists a
, if there exists a  , such that
, such that
![]()
Note that in the above Lipschitz condition, the right hand side does not have any explicit appearance of  , and the
, and the  in the two terms of the left hand side are the same. For ODEs
in the two terms of the left hand side are the same. For ODEs  , where
, where  satisfies the Lipschitz condition, there is a result stronger than Theorem A.1, which guarantees not only existence but also uniqueness of the solution.
satisfies the Lipschitz condition, there is a result stronger than Theorem A.1, which guarantees not only existence but also uniqueness of the solution.
The continuity requirement of this theorem for  can be relaxed as long as discontinuities constitute a null-measure set [72]. A measure is a function that assigns a non-negative real number or
can be relaxed as long as discontinuities constitute a null-measure set [72]. A measure is a function that assigns a non-negative real number or  to (certain) subsets of a set
to (certain) subsets of a set  [210,226]. It must assign zero to the empty set and be (countably) additive: the measure of a “large” subset that can be decomposed into a finite (or countable) number of “smaller” disjoint subsets is the sum of the measures of the “smaller” subsets. Thus, a measure on a set is a systematic way to assign a number to each suitable subset of that set, intuitively interpreted as its size [210,226]. Any set of measure zero is called a null-set (or simply a null-measure set).
[210,226]. It must assign zero to the empty set and be (countably) additive: the measure of a “large” subset that can be decomposed into a finite (or countable) number of “smaller” disjoint subsets is the sum of the measures of the “smaller” subsets. Thus, a measure on a set is a systematic way to assign a number to each suitable subset of that set, intuitively interpreted as its size [210,226]. Any set of measure zero is called a null-set (or simply a null-measure set).
A.4. Linear Ordinary Differential Equations
In this section, we review some elements of the theory of systems of linear ODEs. These can be helpful in the understanding of the content of Chapters 3, 6 and 7, where systems of ODEs emerge.
Consider the first-order system of linear ODEs as in (A.4). Using a matrix representation, we can rewrite (A.4) in the form
![]()
where  and
and  are
are  -dimensional vectors of continuous functions from
-dimensional vectors of continuous functions from 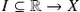 , and for finite dimensional
, and for finite dimensional  ,
,  is the
is the  matrix
matrix  where
where  are all real-valued and continuous. Consider the initial condition of
are all real-valued and continuous. Consider the initial condition of  . The existence and uniqueness of the solution to this IVP follows from Theorem A.2. Since the functions are linear, they automatically satisfy the Lipschitz condition, with
. The existence and uniqueness of the solution to this IVP follows from Theorem A.2. Since the functions are linear, they automatically satisfy the Lipschitz condition, with  associated with the supremum/maximum of
associated with the supremum/maximum of  ’s norm over the compact interval mentioned in the statement of Theorem A.2.
’s norm over the compact interval mentioned in the statement of Theorem A.2.
When  is identically zero, the resulting linear ODE,
is identically zero, the resulting linear ODE,  , is called homogeneous linear ODE . Then,
, is called homogeneous linear ODE . Then,  is the unique solution of the homogeneous linear ODE with the initial state of
is the unique solution of the homogeneous linear ODE with the initial state of  . Clearly, addition of a solution of a linear ODE with any solution of its associated homogeneous linear ODE leads to a new solution of that linear ODE. Moreover, subtraction of two solutions of a linear ODE results in a solution of its associated homogeneous counterpart. The solution space of the homogeneous linear ODE forms a vector space. Let
. Clearly, addition of a solution of a linear ODE with any solution of its associated homogeneous linear ODE leads to a new solution of that linear ODE. Moreover, subtraction of two solutions of a linear ODE results in a solution of its associated homogeneous counterpart. The solution space of the homogeneous linear ODE forms a vector space. Let 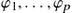 be
be  solutions of the homogeneous linear ODE
solutions of the homogeneous linear ODE  . Then
. Then  are linearly independent at each
are linearly independent at each  if and only if they are linearly independent at some point
if and only if they are linearly independent at some point  . The proof of this key result can be found in [73, 2.8.2]. Therefore, if
. The proof of this key result can be found in [73, 2.8.2]. Therefore, if  has finite dimension
has finite dimension  and
and  are
are  linearly independent solutions of the homogeneous linear ODE, then every other solution of it can be written as a unique linear combination of
linearly independent solutions of the homogeneous linear ODE, then every other solution of it can be written as a unique linear combination of  , which is known as the general solution of the homogeneous linear ODE. Hence, if
, which is known as the general solution of the homogeneous linear ODE. Hence, if 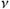 is a solution of the nonhomogeneous linear ODE (called a particular solution ), then every solution of the nonhomogeneous problem
is a solution of the nonhomogeneous linear ODE (called a particular solution ), then every solution of the nonhomogeneous problem  is the sum of the general solution of the associated homogeneous problem and a particular solution, i.e.
is the sum of the general solution of the associated homogeneous problem and a particular solution, i.e.  for a unique set of scalars
for a unique set of scalars  .
.
The solution of the IVP  ,
,  , can be expressed as the following:
, can be expressed as the following:

where 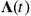 is a fundamental kernel1 of the linear transformation associated with
is a fundamental kernel1 of the linear transformation associated with  . When
. When  has a finite dimension equal to
has a finite dimension equal to  ,
,  is a matrix whose columns are the coordinates of
is a matrix whose columns are the coordinates of  linearly independent solutions of the homogeneous linear ODE
linearly independent solutions of the homogeneous linear ODE  . Additionally, when the coefficients of the linear ODE are constant, i.e. we have an autonomous linear ODE , the basis-forming solutions of the homogeneous ODE
. Additionally, when the coefficients of the linear ODE are constant, i.e. we have an autonomous linear ODE , the basis-forming solutions of the homogeneous ODE  are of the form
are of the form  for
for  and
and  for polynomials
for polynomials  of degree of at most
of degree of at most  , where
, where  are the distinct eigenvalues of matrix
are the distinct eigenvalues of matrix  , and
, and  are their respective multiplicity.
are their respective multiplicity.
A.5. Stability
Consider the autonomous ODE of  (where there is no explicit dependence of
(where there is no explicit dependence of  on
on  ) with the solution of
) with the solution of  for the initial value of
for the initial value of  . Then a point
. Then a point  is an equilibrium (also known as a steady state, fixed point, or critical state) if the constant function
is an equilibrium (also known as a steady state, fixed point, or critical state) if the constant function 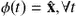 , is a solution of the ODE with the initial condition
, is a solution of the ODE with the initial condition  , i.e. the solution remains at
, i.e. the solution remains at  if it starts there as the initial state. We say an equilibrium
if it starts there as the initial state. We say an equilibrium  is stable if any solution of the IVP
is stable if any solution of the IVP  ,
,  with
with  close to
close to  remains in a small neighborhood of
remains in a small neighborhood of  for all
for all  . It is further called asymptotically stable if it is stable and there is a small neighborhood of
. It is further called asymptotically stable if it is stable and there is a small neighborhood of  such that if the initial value
such that if the initial value  is in that neighborhood we have
is in that neighborhood we have  .
.
The following result governs the stability of equilibrium points derived from  :
:
It should be noted that a finite dimensional space is assumed. In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector-valued function. Specifically, suppose  is a function which takes as input the vector
is a function which takes as input the vector  and produces as output the vector
and produces as output the vector  . Then, the Jacobian matrix
. Then, the Jacobian matrix  of
of  is an
is an 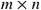 matrix, usually defined and arranged as follows:
matrix, usually defined and arranged as follows:
 (A.5)
(A.5)
The Jacobian matrix is important because if the function  is differentiable at a point
is differentiable at a point  (this is a slightly stronger condition than merely requiring that all partial derivatives exist there), then the Jacobian matrix defines a linear map
(this is a slightly stronger condition than merely requiring that all partial derivatives exist there), then the Jacobian matrix defines a linear map  , which is the best linear approximation of the function
, which is the best linear approximation of the function  near the point
near the point  . This linear map is thus the generalization of the usual notion of derivative and is called the derivative or the differential of
. This linear map is thus the generalization of the usual notion of derivative and is called the derivative or the differential of  at
at  .
.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
