4.4. Malware Diffusion Modeling in Dynamic Networks with Churn

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Summarizing the most important findings emerging from the numerical results presented for malware propagation in wireless distributed networks:

• The behavior of the network is more sensitive to changes in the ratio

λ ∕ μ

$λ ∕ μ$

than to changes in the transmission radius

R

$R$

as far as the pandemic state is concerned.

• The effect of

λ ∕ μ

$λ ∕ μ$

E [L_{I}]

$E [L_{I}]$

is greater than the effect of

R

$R$

when all the other parameters remain constant.

• The network density emerges again as more influential than the link infection rate for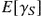

E [γ_{S}]

$E [γ_{S}]$

4.4. Malware Diffusion Modeling in Dynamic Networks with Churn

As explained extensively in the previous parts of the book, modeling accurately the dynamics of malware spreading is of high research and practical importance with numerous associated benefits. This is even more important for dynamic networks with churn (node or edge churn) [6,173], where the impact of malware can be more severe. In this subsection, we focus on touching exactly this aspect of modeling malware dynamics, namely, modeling malware diffusion dynamics in dynamic networks. Such topologies with network churn emerge in most of the applications of complex networks and especially wireless multihop topologies, e.g. ad hoc, sensor, and vehicular, due to a multitude of reasons [203], such as wireless environment variations, device energy variations, as the outcome of malware attacks, and due to user patterns. The churn rate (sometimes called attrition rate), in its broadest sense, is a measure of the number of individuals or items moving out of a collective group over a specific period of time. In that sense, network churn describes the process of nodes (or edges) of the network entering it or leaving it dynamically in a certain period of time.

In the past, various attempts to model malware have emerged (see [223] and references therein, and Part 1 of this book), each aiming at different objectives and employing different tools [58] (Part 1, Chapter 3). However, all this prior work has not studied explicitly network churn. Lately, some notable effort has been devoted to the macroscopic dynamics of malware propagation, where the term macroscopic modeling is meant in the sense of the aggregate study of malware propagation (interested in the number of nodes in each state, not what the exact state of each node is) for a long time period, where different types of attacks spread and present recurring behavior. Such efforts have especially focused on wireless decentralized networks, as partially shown in the previous subsections of this chapter and the various works available in the literature, e.g. [119,133] and references therein.

This subsection presents and analyzes modeling approaches that extend the queuing-based modeling of malware diffusion presented in the previous subsections of this chapter and analyze the macroscopic modeling of malware propagation for complex communication networks with churn, i.e. wireless ad hoc, SF, SW, and random topologies. In the considered framework, legitimate nodes might enter/leave the network due to exhausting their energy/recharging and/or the impact of malware. As in the previous models in this chapter, a queuing network model is again used to capture the transitions of states of legitimate nodes attacked by malicious users. To treat this problem, an open queuing network model is presented for the behavior of legitimate nodes attacked by malicious users, in contrast to the models presented previously where a closed queuing system was sufficient, due to the lack of churn. As before, a product-form solution of the presented model is obtained through the Norton equivalent model, and the dynamics of spreading are studied. The results can be used for assessing the robustness of arbitrary complex networks under diverse operational scenarios.

The results yielded by this approach can be used again for assessing the robustness of the network and can be further exploited in increasing network reliability against the worst possible outbreaks. Given also that very few approaches in the literature have addressed malware diffusion modeling for dynamic networks with churn [121,122], the value of this framework is of great interest for both academics and the industry.

4.4.1. Malware Diffusion Models and Network Churn

As mentioned in Part 1, malware can be broadly classified in two main types, i.e. direct and indirect, where threats propagate via physical neighbors only [199], or via multihop infections, e.g. email viruses [233]. In the following, the focus will continue being put on propagation via physical neighbor contact, since the other type can be implicitly analyzed as a case of direct malware spreading at a higher protocol layer.

Furthermore, with respect to the SIR and SIS infection models, the first is more suitable for the short-term study of independent threats, while the second is more appropriate for the long-term (macroscopic) study of mixing threats. In the macroscopic study of malware diffusion, nodes oscillate between susceptibility and infection due to recurrent or newly emerging malware. Currently, network churn can be only studied within the framework of the macroscopic malware diffusion study [121,122], and thus the following analysis will focus on the long-term and steady-state behavior of complex networks. For this reason, the SIS node infection paradigm is adopted here too.

As explained in the previous subsection, in accord with the importance of complex network infrastructures, more generic approaches analyzing malware propagation are required to secure commercial and critical networks. Probabilistic tools have been mostly employed as alternatives to the more popular deterministic models relying on systems of differential equations, e.g. probabilistic models based on interactive Markov chains proposed in [82], or a stochastic optimization framework introduced in [132,133], which will be described in detail in Chapter 6. Similarly, in the previous subsections of this chapter, a queuing-based framework has been proposed in [124] for wireless multihop networks. This last modeling approach can be exploited in various capacities, as it will be shown in Chapter 9. The approach presented next adopts the same framework but extends it in the more general scenario of dynamic networks with node churn.

The most general behavior of dynamic networks, where legitimate nodes enter/leave the network due to their own operation (e.g. exhausting network energy) and/or the impact of malware, is considered. The approach that will be presented in the following, was developed in [121,122] and extended the framework of [119] for networks with churn, further applying it in various types of complex communications networks.

4.4.2. Open Queuing Network Theory for Modeling Malware Spreading in Complex Networks with Churn

In this subsection and the rest of the chapter, we focus on the case of nonpropagative networks where malware spreading takes place under the SIS infection model for describing the macroscopic behavior of users. A static wireless distributed network with churn [104], modeling, e.g. a sensor or ad hoc network, is considered.

In a network with churn and under the SIS paradigm, a legitimate node will start susceptible, clear of any malware, denoting the corresponding susceptible state by S (Fig. 4.21). At some point, a susceptible node will become infected by some spreading threat, e.g. virus and worm, and within a long observation period, the node will eventually return to the susceptible state (by removing the malware). The infected state is denoted by I. In the general case of networks with churn, but also for networks without churn, the short-term behavior of nodes and their corresponding state transition may involve other intermediate or terminal states as well, as shown in Fig. 4.21. These transitions may involve an intermediate recovery state (denoted by R) and a terminal state where nodes are considered dead (denoted by D). The dead state cumulatively represents nodes that cease operation due to exhausted energy or due to malware operation. Nodes that complete their recovery, return to the susceptible state, and without loss of generality, it is assumed that new nodes entering the network also begin their lifetime in the susceptible state. Dead nodes are completely removed from the network (potentially reintroduced in the network as new susceptibles after a long time, partially constituting the set of new nodes). Consequently, the overall system follows the SIS paradigm, where it will be possible for susceptible nodes to become infected and eventually recover again to the susceptible state.

Fig. 4.21 — FIGURE 4.21 State-transition diagram for legitimate nodes in a network with churn. Courtesy Karyotis V, Papavassiliou S. Evaluation of malware spreading in wireless multihop networks with churn. In: Proceedings of 6th international conference on ad hoc networks (EAI ADHOCNETS). Springer; 2014. With kind permission from Springer Science and Business Media.

Regarding the communication model, we assume that at each time the network has

n = n (t)

$n = n (t)$

legitimate nodes, each with transmission radius

R_{trans}

$R_{trans}$

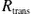. Whenever there is no danger of ambiguity, we drop the time dependence from the symbol of the total number of network nodes at each time instant,

n (t)

$n (t)$

. For simplicity, it is also assumed that node pairs are formed only within the transmission range of devices, as in [117–119,133]. More general communication models can be incorporated in a straightforward manner.

With respect to Fig. 4.21, it can be observed that each user spends an amount of time in each node state that varies stochastically. Furthermore, given the succession of state transitions depicted in Fig. 4.21, a node entering the network at the susceptible state might either deplete its energy and become dead with probability

p

$p$

or could become infected by malware and transition to the infected state. From the infected state, the node might either deplete its energy as well, cease operation due to malware and become dead with probability

q

$q$

, or it could transition to the recovery state. Finally, from the recovering state, the user either recovers to the susceptible state and the cycle begins again, or the node depletes its energy while recovering and it is removed from the network to the dead state with probability

w

$w$

Thus, the behavior of legitimate users can be segregated in two main modes, susceptible and infected-recovering. In the first mode, nodes can be operational (some of which might exhaust their energy and leave the network) or recharging (considered semi-operational). In the infected-recovering mode, nodes become infected and either they move to recovery until they become susceptible again or they are removed due to malware or exhausting their energy.

This behavior can be mapped to the operation of a queuing network as shown in Fig. 4.22(a)[121,122], where queuing and processing correspond to the time spent by each node in each different state described before. In Fig. 4.22(a), the upper part corresponds to the normal operation of nodes (susceptible operational-susceptible recharging) and the lower part to the infection-recovery mode. The customers of the queuing network correspond to the nodes of the network as they change states due to malware and node churn. It should be noted that the queuing network is open due to node churn, allowing for new customers to enter (corresponding to new susceptible nodes) and customers to leave (corresponding to nodes depleting their energy or becoming dead due to malware).

The depicted input/output rates of the network in Figs 4.22(a) and 4.22(b) correspond to node churn rates, while the arrival/service rates at each queue correspond to the infection/recovery processes of the legitimate nodes of the actual network under attack. Starting with Fig. 4.22(a),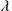

λ

$λ$

is the rate at which new nodes emerge in the network, while

p, q, w

$p, q, w$

is the probability for a node to exit the network at the susceptible, infected, and recovering states, respectively. The sum

p + q + w

$p + q + w$

corresponds to the total rate at which nodes leave the network. Thus,

λ ∕ (p + q + w)

$λ ∕ (p + q + w)$

determines the total node churn rate of the network. In the block of the susceptible queues (upper block) in Fig. 4.22(a),

λ_{s}^{o}

$λ_{s}^{o}$

is the effective rate at which nodes recover to the operational-susceptible state (after churn has been taken into account) and

λ_{s}^{r}

$λ_{s}^{r}$

is the effective rate at which nodes recover to the recharging susceptible state. Similarly,

μ_{s}^{o}

$μ_{s}^{o}$

is the infection rate of susceptible operational nodes, while

μ_{s}^{r}

$μ_{s}^{r}$

is the infection rate of susceptible recharging nodes. When combined, rate

λ_{S} = λ_{s}^{o} + λ_{s}^{r}

$λ_{S} = λ_{s}^{o} + λ_{s}^{r}$

is the effective recovery rate of nodes to the susceptible state and

μ_{S} = μ_{s}^{o} + μ_{s}^{r}

$μ_{S} = μ_{s}^{o} + μ_{s}^{r}$

is the total infection rate of susceptible nodes (Fig. 4.22(b)). With respect to the lower tandem queues,

λ_{I}

$λ_{I}$

is the effective infection rate (rate of infection of susceptible nodes after node churn has been calculated),

μ_{R}

$μ_{R}$

is the total rate of nodes out of the infected state,

λ_{R}

$λ_{R}$

the effective rate under which nodes enter the recovery state (after node churn has been calculated), and

μ_{R}

$μ_{R}$

the total rate out of the recovery state. In Fig. 4.22(b),

n_{S}, n_{I}, n_{R}

$n_{S}, n_{I}, n_{R}$

is the total number of susceptible, infected, and recovering nodes at the moment, respectively.

In order to analyze the generic network of Fig. 4.22(a), the Norton equivalent of the upper part with parallel queues may be employed, yielding eventually the queuing network of Fig. 4.22(b)[121,122]. This does not harm the analysis because in malware dynamics and robustness analysis we are not particularly interested in which nodes are susceptible-operational and which are susceptible-recharging, focusing on the total number of susceptible users. We consider the number of susceptible nodes versus the number of infected and recovering, as in the queuing network of Fig. 4.22(b). Not shown in Fig. 4.22 is the parameter of the link infection rate of a susceptible (denoted by

λ_{e}

$λ_{e}$

), which corresponds to the link infection rate

λ_{k}

$λ_{k}$

for each link of a node in the malware to queuing mapping in Fig. 4.1. Also not shown, the service rates in the infected (

μ_{i}

$μ_{i}$

) and recovering (

μ_{r}

$μ_{r}$

) queues of each individual node. The rates defined previously and shown in Figs 4.22(a) and 4.22(b) correspond to the cumulative queue service rates, which in turn depend on the partial rates of

λ_{e}

$λ_{e}$

μ_{i}

$μ_{i}$

, and

μ_{r}

$μ_{r}$

of each node. Without loss of generality, these partial rates are considered the same for all users.

FIGURE 4.22 Queuing models for malware spreading in networks with churn. From^© 2015 IEEE. Reprinted, with permission, from Karyotis V, Papavassiliou S. Macroscopic malware propagation dynamics for complex networks with churn. IEEE Commun Lett 2015;19(4):577–80.

Fig. 4.22a — (a) Generic malware propagation queuing model.

Fig. 4.22b — (b) Norton equivalent queuing model.

Fig. 4.22c — (c) Equivalent product-form serial queuing system.

The model in Fig. 4.22(a) (and the Norton equivalent) can be analyzed using Jackson’s theorem for product-form networks [25]. It should be also noted that all initial services are exponential with rates as shown in Fig. 4.22(a). The combined inputs are not Poisson, thus nor are the outputs. However, each queue behaves as an

M ∕ M ∕ r_{i}

$M ∕ M ∕ r_{i}$

queue with specific input and output, as will be explained shortly, where

r_{i}

$r_{i}$

is the number of servers of each queuing stage (

r_{1} = 2, r_{2} = r_{3} = 1

$r_{1} = 2, r_{2} = r_{3} = 1$

Regarding node churn, we study the system for a churn rate

λ ∕ (p + q + w) \approx 1

$λ ∕ (p + q + w) \approx 1$

, which means that the network will remain approximately the same, on average, avoiding degenerate topologies (too big or disconnected), while allowing numerous churn operations. Thus, it will be possible to evaluate various complex network types, where node churn emerges naturally, i.e. random, small-world, and scale-free networks.

4.4.3. Analysis of Malware Propagation in Networks with Churn

The queuing network of Fig. 4.22(b) has a product-form steady-state distribution and it is equivalent to a network of three cascade queues as shown in Fig. 4.22(c)[121,122]. The service rates of the final cascade network are directly obtained from the Norton equivalent of Fig. 4.22(b), as

μ_{1} = μ_{S}, μ_{2} = μ_{I}, μ_{3} = μ_{R}

$μ_{1} = μ_{S}, μ_{2} = μ_{I}, μ_{3} = μ_{R}$

. The arrival rates in the product-form network (Fig. 4.22(c)) in the general case can be obtained as

$λ_{i} = λ_{i}^{'} + \sum_{k = 1}^{3} q_{k i} λ_{k}, i, k = 1, 2, 3,$ $λ_{i} = λ_{i}^{'} + \sum_{k = 1}^{3} q_{k i} λ_{k}, i, k = 1, 2, 3,$

(4.24)

where

λ_{i}^{'}

$λ_{i}^{'}$

are potential external inputs to each stage (here only

λ_{1}^{'} = λ

$λ_{1}^{'} = λ$

, corresponding to the input of new susceptible nodes and the rest external inputs are considered zero), and

q_{k i}

$q_{k i}$

is the probability for a customer to move from stage

k

$k$

to stage

i

$i$

. From this,

1 - \prod_{k} (1 - \sum_{i} q_{k i})

$1 - \prod_{k} (1 - \sum_{i} q_{k i})$

is the probability that the customer (network node in the malware context) stays in the system (

1 - \sum_{i} q_{k i}

$1 - \sum_{i} q_{k i}$

is the probability for the customer to leave the system at stage

k

$k$

). Solving the corresponding system of equations, we obtain

$λ_{1} = \frac{1}{1 - (1 - p) (1 - q) (1 - w)} λ,$ $λ_{1} = \frac{1}{1 - (1 - p) (1 - q) (1 - w)} λ,$

(4.25)

$λ_{2} = \frac{(1 - p)}{1 - (1 - p) (1 - q) (1 - w)} λ,$ $λ_{2} = \frac{(1 - p)}{1 - (1 - p) (1 - q) (1 - w)} λ,$

(4.26)

$λ_{3} = \frac{(1 - p) (1 - q)}{1 - (1 - p) (1 - q) (1 - w)} λ .$ $λ_{3} = \frac{(1 - p) (1 - q)}{1 - (1 - p) (1 - q) (1 - w)} λ .$

(4.27)

The steady-state distribution of the cascade product-form network will be of the form

$p (n_{1}, n_{2}, n_{3}) = p_{1} (n_{1}) p_{2} (n_{2}) p_{3} (n_{3}),$ $p (n_{1}, n_{2}, n_{3}) = p_{1} (n_{1}) p_{2} (n_{2}) p_{3} (n_{3}),$

(4.28)

where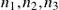

n_{1}, n_{2}, n_{3}

$n_{1}, n_{2}, n_{3}$

are the number of users in the susceptible, infected, and recovering states, respectively, and at every time instant

n_{1} + n_{2} + n_{3} = n (t)

$n_{1} + n_{2} + n_{3} = n (t)$

. Jackson’s theorem allows to treat each stage (queue in Fig. 4.22(c)) as an independent

M ∕ M ∕ r_{i}

$M ∕ M ∕ r_{i}$

queue with input rate

λ_{i}

$λ_{i}$

and service rate

μ_{i}

$μ_{i}$

i = 1, 2, 3

$i = 1, 2, 3$

. An input policy regulating the arrival of new susceptible nodes with respect to the death/removal rates should be employed to ensure

n (t) < \infty

$n (t) < \infty$

, complying with realistic networks that typically have finite nodes. Distribution

p_{i} (n_{i})

$p_{i} (n_{i})$

provides the number of users in each queue, and in the general form where all service rates of a block (stage) with

r_{i}

$r_{i}$

parallel queues are the same, it is obtained as

$p_{i} (n_{i}) = {\begin{matrix} \frac{{(λ_{i} ∕ μ_{i})}^{n_{i}}}{n_{i}!} p_{i, 0}, & n_{i} < r_{i} \\ \frac{r_{i}^{r_{i}} ρ_{i}^{n_{i}}}{r_{i}!} p_{i, 0}, & n_{i} \geq r_{i} \end{matrix},$ $p_{i} (n_{i}) = {\begin{matrix} \frac{{(λ_{i} ∕ μ_{i})}^{n_{i}}}{n_{i}!} p_{i, 0}, & n_{i} < r_{i} \\ \frac{r_{i}^{r_{i}} ρ_{i}^{n_{i}}}{r_{i}!} p_{i, 0}, & n_{i} \geq r_{i} \end{matrix},$

(4.29)

$p_{i, 0} = \frac{1}{\sum_{n = 0}^{r_{i} - 1} \frac{{(λ_{i} ∕ μ_{i})}^{n}}{n!} + \frac{{(λ_{i} ∕ μ_{i})}^{r_{i}}}{r_{i}! (1 - ρ_{i})}},$ $p_{i, 0} = \frac{1}{\sum_{n = 0}^{r_{i} - 1} \frac{{(λ_{i} ∕ μ_{i})}^{n}}{n!} + \frac{{(λ_{i} ∕ μ_{i})}^{r_{i}}}{r_{i}! (1 - ρ_{i})}},$

(4.30)

where

ρ_{i} = λ_{i} ∕ r_{i} μ_{i}

$ρ_{i} = λ_{i} ∕ r_{i} μ_{i}$

. In our case,

r_{1} = 2, r_{2} = r_{3} = 1

$r_{1} = 2, r_{2} = r_{3} = 1$

(Fig. 4.22(a)). However, the service rates of the two parallel queues in stage 1 are not the same. Thus, the above expressions may be used directly for obtaining the distributions of stages 2 and 3, while for the first stage, we consider the system as an

M ∕ M ∕ 2

$M ∕ M ∕ 2$

queue with different service rates for the two servers and solve explicitly for its steady-state distribution. At this point, it should be noted that due to the simplification of the generic model in Fig. 4.22(a) into the Norton equivalent shown in Fig. 4.22(b), for the computation of the corresponding expression, arriving customers have no memory, i.e. they choose randomly which server to join if they find an empty system. This comes at the cost that with the equivalent model we cannot explicitly track which node recovers to the operational-susceptible state and which to the recharging susceptible, but as mentioned above, we sacrifice this analytic detail of the original model for the sake of obtaining explicit analytic results eventually. Consequently, the corresponding expression is obtained,

$p_{1} (n_{1}) = {\begin{matrix} {[1 + \frac{C}{ρ_{1} (1 - ρ_{1})}]}^{- 1}, & n_{1} = 0 \\ \frac{C}{ρ_{1} + \frac{C}{1 - ρ_{1}}}, & n_{1} = 1, \\ ρ_{1}^{n - 2} \frac{C}{1 + \frac{C}{ρ_{1} (1 - ρ_{1})}}, & n_{1} \geq 2 \end{matrix}$ $p_{1} (n_{1}) = {\begin{matrix} {[1 + \frac{C}{ρ_{1} (1 - ρ_{1})}]}^{- 1}, & n_{1} = 0 \\ \frac{C}{ρ_{1} + \frac{C}{1 - ρ_{1}}}, & n_{1} = 1, \\ ρ_{1}^{n - 2} \frac{C}{1 + \frac{C}{ρ_{1} (1 - ρ_{1})}}, & n_{1} \geq 2 \end{matrix}$

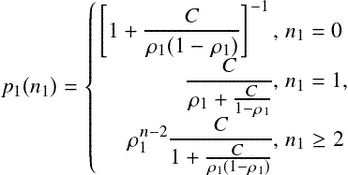(4.31)

where

ρ_{1} = λ_{1} ∕ μ_{1}

$ρ_{1} = λ_{1} ∕ μ_{1}$

C

$C$

is a constant depending on

λ_{1}, μ_{1}

$λ_{1}, μ_{1}$

, given by

$C = \frac{λ_{1}^{2}}{2 μ_{s}^{o} μ_{s}^{r}},$ $C = \frac{λ_{1}^{2}}{2 μ_{s}^{o} μ_{s}^{r}},$

(4.32)

and for the second and third stages, we obtain the distributions directly as geometric expressions of

M ∕ M ∕ 1

$M ∕ M ∕ 1$

queues, respectively,

$p_{2} (n_{2}) = ρ_{2}^{n_{2}} (1 - ρ_{2}),$ $p_{2} (n_{2}) = ρ_{2}^{n_{2}} (1 - ρ_{2}),$

(4.33)

$p_{3} (n_{3}) = ρ_{3}^{n_{3}} (1 - ρ_{3}),$ $p_{3} (n_{3}) = ρ_{3}^{n_{3}} (1 - ρ_{3}),$

(4.34)

where

ρ_{2} = λ_{2} ∕ μ_{2}

$ρ_{2} = λ_{2} ∕ μ_{2}$

ρ_{3} = λ_{3} ∕ μ_{3}

$ρ_{3} = λ_{3} ∕ μ_{3}$

ρ_{1}, ρ_{2}, ρ_{3} < 1

$ρ_{1}, ρ_{2}, ρ_{3} < 1$

, and

n_{1}, n_{2}, n_{3} \geq 0

$n_{1}, n_{2}, n_{3} \geq 0$

In Fig. 4.22(c),

n_{1}

$n_{1}$

refers to susceptible,

n_{2}

$n_{2}$

to infected, and

n_{3}

$n_{3}$

to recovering nodes, respectively. The number of dead nodes is unimportant, since they do not participate in malware dynamics and in addition, it is assumed that new nodes are always available. The service rate of each queue in Fig. 4.22(c) is as shown in Fig. 4.22(b), which is the Norton equivalent service rate from Fig. 4.22(a). The service rates in the original queuing network depend on the infection model, malware potentials, and the topology of each network.

The average number of users in such system is given by

$L = \sum_{i = 1}^{m} L_{i} = L_{1} + \sum_{i = 2}^{3} p_{r_{i}} \frac{ρ_{i}}{{(1 - ρ_{i})}^{2}},$ $L = \sum_{i = 1}^{m} L_{i} = L_{1} + \sum_{i = 2}^{3} p_{r_{i}} \frac{ρ_{i}}{{(1 - ρ_{i})}^{2}},$

(4.35)

where

L_{i}

$L_{i}$

is the average number of users in each queue and

p_{r_{i}} = \frac{{(λ_{i} ∕ μ_{i})}^{r_{i}}}{r_{i}!} p_{i, 0}

$p_{r_{i}} = \frac{{(λ_{i} ∕ μ_{i})}^{r_{i}}}{r_{i}!} p_{i, 0}$

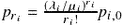. In this case, the average number of susceptible (operational) and infected-recovering nodes is

$L_{1} = \frac{C (1 - ρ_{1})}{ρ_{1} (1 - ρ_{1}) + C} [1 + \frac{ρ_{1} (2 - ρ_{1})}{{(1 - ρ_{1})}^{2}}],$ $L_{1} = \frac{C (1 - ρ_{1})}{ρ_{1} (1 - ρ_{1}) + C} [1 + \frac{ρ_{1} (2 - ρ_{1})}{{(1 - ρ_{1})}^{2}}],$

(4.36)

$L_{2} = \frac{ρ_{2}}{1 - ρ_{2}},$ $L_{2} = \frac{ρ_{2}}{1 - ρ_{2}},$

(4.37)

$L_{3} = \frac{ρ_{3}}{1 - ρ_{3}} .$ $L_{3} = \frac{ρ_{3}}{1 - ρ_{3}} .$

(4.38)

Using the customer distributions (4.31) and (4.34), other quantities of interest can be computed, e.g. the average throughput of stage 1, which provides the average total infection rate of the system. Similarly, the average throughput of stage 3 provides the average recovery rate of the system, while the average throughput of stage 2 the average healing rate of infected nodes. Summing up these throughput quantities, weighted by the corresponding loss probabilities

p, q, w

$p, q, w$

, the corresponding cumulative node loss churn rate can be obtained.

Until this point, the analysis is generic and applies to all types of networks with churn (centralized, multihop, small-world, scale-free, etc.). However, the model developed in Fig. 4.22 allows more specific results to be obtained on a per network case. For instance, apart from

n_{1}

$n_{1}$

n_{2}

$n_{2}$

n_{3}

$n_{3}$

, one may obtain analytical expressions of the average

n_{2}

$n_{2}$

with respect to network parameters, such as the node transmission radius and node densities of a specific wireless network. Such task is network type/scenario specific depending on the topology and operation of each network. For instance, in order to obtain the above for an ad hoc network, the Norton equivalent of Fig. 4.22(b) will be required to be further substituted with another Norton equivalent closed queuing network were two adjacent queues are substituted with an equivalent queue, yielding eventually a two-queue network with feedback, which can be easily solved via standard Markov chain methods to obtain the steady-state distribution of the queue of interest with respect to all involved network parameters. Then, additional quantities/rates can yield other desired dynamics of the corresponding systems.

4.4.4. Demonstration of Queuing Framework for Malware Spreading in Complex and Wireless Networks

In this section, numerical and simulation results regarding the operation and behavior of complex and wireless distributed networks with churn when attacked by a single attacker are presented. Infected nodes are assumed to further propagate the infectious malware they received, while recovering nodes are prevented from doing so. This means that the spreading of malware is mainly due to the network, while the attacker has a smaller role in spreading dynamics, mostly needed to generate new infections in the event that a network manages to recover completely for an instance. Thus, the network spreading dynamics will be studied in the following.

The evaluation is based on a Matlab simulator, developed for studying the behavior of the attacked network [121,122]. At each epoch (slot) of the simulator one event took place, according to the current state of the system

{n_{1}, n_{2}, n_{3}}

${n_{1}, n_{2}, n_{3}}$

, the topology of the network and the corresponding infection (S

\to

$\to$

I transition), recovering (I

\to

$\to$

R transition), and full-recovery (R

\to

$\to$

S transition) rates. This was ensured by the nature of the system in Fig. 4.22.

For the multihop networks we focus on, the link infection rate

λ_{e}

$λ_{e}$

of a susceptible node represents the probability that this user will become infected from a malicious neighbor. The multihop topology is considered for this case as a random geometric graph. Combining this with the link infection, a detailed analysis of the system in Fig. 4.22(a) yields the total infection rate, as the service rate of the single queue of susceptible nodes in the Norton equivalent (which is equal to

μ_{1}

$μ_{1}$

in the product-form equivalent). This infection rate will be

\sum_{m = 1}^{n_{1}} k_{m} λ_{e}

$\sum_{m = 1}^{n_{1}} k_{m} λ_{e}$

, where

k_{m}

$k_{m}$

is the number of malicious neighbors of susceptible node

m

$m$

(counting both the attacker and infected legitimate nodes). The total recovering (corresponding to

μ_{2}

$μ_{2}$

in Fig. 4.22(c)) and full-recovery rates (corresponding to

μ_{3}

$μ_{3}$

in Fig. 4.22(c)) depend on

n_{2}

$n_{2}$

n_{3}

$n_{3}$

, and may be computed as

n_{2} μ_{i}

$n_{2} μ_{i}$

n_{3} μ_{r}

$n_{3} μ_{r}$

, respectively.

In this book, only some indicative results are provided, which however can be used for the assessment of network reliability and attack potentials. Regarding node churn, we study the behavior of the system for positive churn, i.e. for a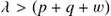

λ > (p + q + w)

$λ > (p + q + w)$

, which means that the networks analyzed were considered to be growing on average. This is preferable for the study, as a decreasing network could sometimes lead to degenerate (disconnected) topologies, or even to the extinction of the network.

Evaluation of malware spreading in complex networks

In this subsection, we initially present some numerical and then simulation results exhibiting the operation of attacked complex networks with churn. For demonstration purposes, we consider some specific types of networks, but any other type of wireless or wired networks is applicable as well. We assume that the network churn parameters are fixed and equal to

λ = 0.25, p = w = 0.05, q = 0.1

$λ = 0.25, p = w = 0.05, q = 0.1$

(for the rest of this chapter, all node rates are assumed to have units “node/time unit”). The loss of infected nodes was considered double than the loss of the rest of node classes, due to two-fold death possibilities (i.e. malware and energy depletion).

Fig. 4.23 presents numerical results obtained from analysis (Eqs (4.36) and (4.38)). Furthermore, it compares with the theoretical results for the same networks but with no churn, obtained previously in Section 4.3.2 and more specifically with numerical results already provided in Section 4.3.2 (also from [119] in the literature) for the case of 800 legitimate nodes. The corresponding curve is denoted in the comparison figure as “infected-no churn.” The percentages of susceptible (

L_{1} ∕ L

$L_{1} ∕ L$

) and infected (

L_{2} ∕ L

$L_{2} ∕ L$

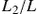) nodes (obtained via Eqs (4.35)–(4.37)) with respect to parameter

λ_{1} ∕ μ_{1}

$λ_{1} ∕ μ_{1}$

denoted as infection-to-recovery strength (horizontal axis in the figure) is shown for two different combinations of the service rate of the infected and the recovering queues (stages 2 and 3). Notice the difference in the two vertical axes scales, while the third percentage of recovering nodes can be computed straightforwardly. In Fig. 4.23(b), the service rate of the recovery stage was double than that in Fig. 4.23(a), which implies a faster transition from recovering to susceptible state, i.e. less recovering but more susceptible nodes. Using results of these types, extensive analyses can be obtained with respect to the expected behavior of the system for various combinations of the parameters involved (churn rates, recovery/infection strengths, etc.), and thus the expected reliability of the network can be assessed. Fig. 4.23 characterizes network-related behavior with respect to attacks.

FIGURE 4.23 Percentage of susceptible and infected nodes versus network infection/recovery strength and comparison with networks with no churn for complex networks. From^© 2015 IEEE. Reprinted, with permission, from Karyotis V, Papavassiliou S. Macroscopic malware propagation dynamics for complex networks with churn. IEEE Commun Lett 2015;19(4):577–80.

Fig. 4.23a — (a) Lower full recovery rate.

Fig. 4.23b — (b) Higher full recovery rate.

Fig. 4.24 presents similar results for three types of complex networks, a random [Erdos-Renyi (ER) model], a small-world [Watts-Strogatz (WS) model], and a scale-free [Barabasi-Albert (BA) model] network. However, now the infection-to-recovery strength is that of a single node, namely, the infection rate at a communication link to the recovery rate of a node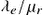

λ_{e} ∕ μ_{r}

$λ_{e} ∕ μ_{r}$

and not that of the network as before. Thus, Fig. 4.24 characterizes node-related behavior with respect to attacks. The total rates

λ_{i}, μ_{i}, i = 1, 2, 3

$λ_{i}, μ_{i}, i = 1, 2, 3$

are functions of

λ_{e}, μ_{r}

$λ_{e}, μ_{r}$

. In general, it is observed that all these types of networks exhibit some form of robustness, maintaining sufficient percentages of susceptible nodes for infection/recovery strengths lower than unity. As the infection/recovery strength increases, the behavior of the three networks seems to converge. In addition, with respect to the percentage of susceptible nodes, the random network seems to be the more robust against generic attacks, followed by the scale-free and then the small-world, since the small-world, and the scale-free to a lesser degree, have structural vulnerabilities (shortcuts and node-hubs, respectively). The latter are in accordance with similar solutions reached in Chapter 5, following a completely different modeling approach.

FIGURE 4.24 Expected percentage of susceptible, infected, and recovering nodes versus infection/recovery strength (simulation) for complex networks with 400 and 800 initial nodes. From^© 2015 IEEE. Reprinted, with permission, from Karyotis V, Papavassiliou S. Macroscopic malware propagation dynamics for complex networks with churn. IEEE Commun Lett 2015;19(4):577–80.

Fig. 4.24a — (a) Random network with edges scaling as $O (n log n)$ $O (n log n)$ .

(a) Random network with edges scaling as $O (n log n)$ $O (n log n)$ .

Fig. 4.24b — (b) Small-world network initial regular lattice with 10 neighbors and $g_{p} = 0.1$ $g_{p} = 0.1$ shortcut probability.

Fig. 4.24c — (c) Scale-free network initially, all nodes connect to 10 other neighbors.

Evaluation of malware spreading in wireless distributed networks

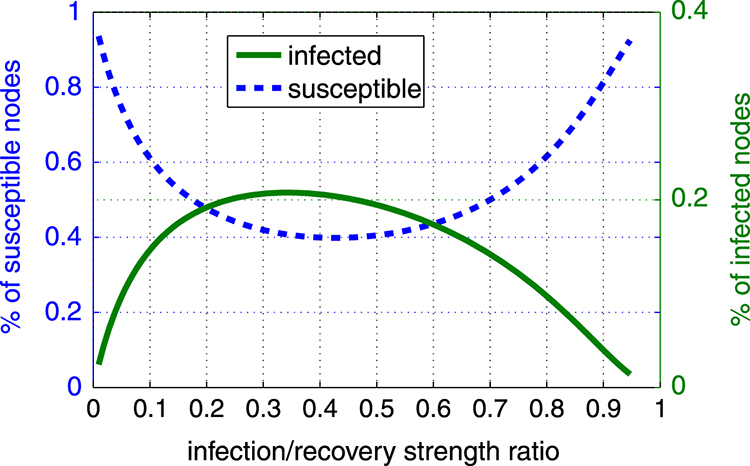
Fig. 4.25 presents some numerical results obtained from the analysis, valid for arbitrary networks, providing intuition on the behavior of the average number of nodes in the states of the system. Churn strength is equal to 1.67, which translates to a growing network. Notice the different scales in the vertical axes in both figures and for both

y

$y$

-axes of each figure, indicating how the expected number of susceptible and infected nodes varies with respect to the time each node is expected to spend in each of the three stages (service rates).

FIGURE 4.25 Percentages of susceptible and infected nodes as a function of infection to recovery strength (numerical) for wireless distributed (multihop) networks. Courtesy Karyotis V, Papavassiliou S. Evaluation of malware spreading in wireless multihop networks with churn. In: Proceedings of 6th international conference on ad hoc networks (EAI ADHOCNETS). Springer; 2014. With kind permission from Springer Science and Business Media.

As expected, a decrease in susceptible nodes translates to an increase in the infected nodes. By comparing Fig. 4.25(a) and Fig. 4.25(b), it can be also observed that regarding the dependence on the infection/recovery strength, some symmetry (Fig. 4.25(b)) should be expected when the recovery (

μ_{I}

$μ_{I}$

) and full-recovery (

μ_{R}

$μ_{R}$

) rates are the same. These results, and many similar that can be obtained from the expressions provided before, can be used to assess the robustness of the network. Malware dynamics are represented via the infection and recovery rates, while the full-recovery rate represents the countermeasures’ efficiency. Thus, given these parameters, the expected state of the system can be evaluated.

The following results have been obtained through simulations for a wireless distributed (random geometric) network, in which a square deployment region with size

L = 1000

$L = 1000$

m was employed and all devices used a transmission radius

R_{t} = 150

$R_{t} = 150$

m. Fig. 4.26 presents the expected number of nodes in each state of the system as a function of network density (we fixed the deployment region and increased progressively network nodes). Fig. 4.26(a) regards a network with uneven recovery-full recovery rates,

μ_{I} - μ_{R}

$μ_{I} - μ_{R}$

, respectively. This means that the mean infection and recovery times will be uneven as well. Fig. 4.26(b) shows the corresponding results for even rates.

FIGURE 4.26 Expected number of nodes in each state of a wireless distributed (multihop) network with respect to network density. Courtesy Karyotis V, Papavassiliou S. Evaluation of malware spreading in wireless multihop networks with churn. In: Proceedings of 6th international conference on ad hoc networks (EAI ADHOCNETS). Springer; 2014. With kind permission from Springer Science and Business Media.

Fig. 4.26a — (a) Uneven recovery-full recovery rates.

Fig. 4.26b — (b) Even recovery-full recovery rates.

It is observed that as the network density increases, so do the expected number of nodes in each state, and such increase is almost linear. However, the corresponding increase rates are different for uneven recovery-full recovery rates and similar for even rates. In both cases, the infection to full recovery strength is

λ_{e} ∕ μ_{r} = 2

$λ_{e} ∕ μ_{r} = 2$

. This scaling behavior explains the fact that the number of infected nodes is the smallest compared to infected and recovering nodes, revealing potential vulnerabilities for the network with respect to the specific malware dynamics and the network structure, as it was also possible to do with the numerical analysis we presented before.

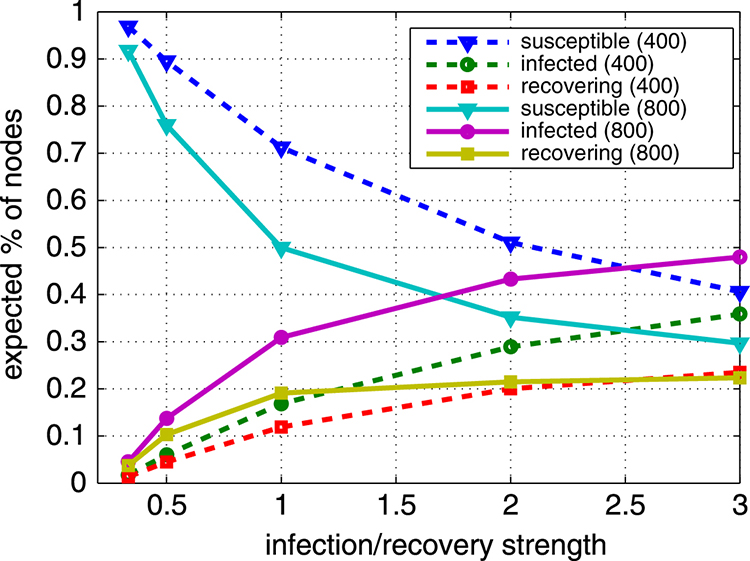
However, different trends emerge regarding the expected number of nodes in each state with respect to the infection/recovery strength, as shown in Fig. 4.27. As before, the expected number of susceptible nodes has a complementary behavior to the expected number of infected and recovering nodes. The trend though is not linear. In fact, the number of recovering nodes, especially in Fig. 4.27(b), seems to saturate for increasing infection/recovery strength. Such results can be again used to evaluate the robustness of the network with respect to the expected behavior under various attack-countermeasure parameters.

FIGURE 4.27 Expected number of nodes in each state of a wireless distributed (multihop) network with respect to infection/recovery rates. Courtesy Karyotis V, Papavassiliou S. Evaluation of malware spreading in wireless multihop networks with churn. In: Proceedings of 6th international conference on ad hoc networks (EAI ADHOCNETS). Springer; 2014. With kind permission from Springer Science and Business Media.

Fig. 4.27a — (a) Even recovery-full recovery rates.

Fig. 4.27b — (b) Uneven recovery-full recovery rates.

Finally, Fig. 4.28 shows the average percentage difference of network size for even/uneven infection/recovery strengths, with respect to node density and the intensity of the infection/recovery strength. The first two bars in Fig. 4.28 are the average node increase as the density of the network increases, while the last two bars represent the average node count increase for increasing infection/recovery strength. As expected, average percentage difference is positive, even though small in some cases (since the churn strength was set slightly higher than 1 in all scenarios to ensure a proper topology). It can be observed that, in general, even infection-recovery strengths yield higher increase than uneven ones. More practically, equal infection/recovery rates correspond to strategies providing countermeasures that match the effect of malware at the same time scales (fast-response), which in turn allow the network to maintain more nodes operational on average, by preventing some I

\to

$\to$

D transitions (infected nodes becoming dead) due to malware.

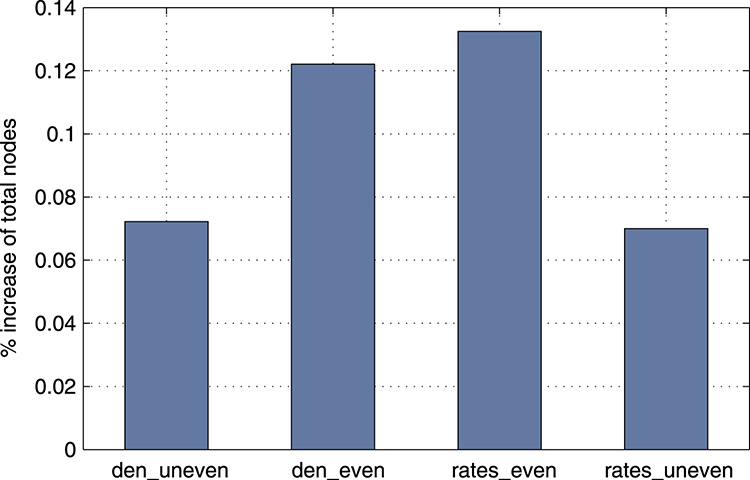
Fig. 4.28 — FIGURE 4.28 Expected percentage variation of the total number of nodes with respect to node density and infection/recovery strength for wireless distributed (multihop) networks. Courtesy Karyotis V, Papavassiliou S. Evaluation of malware spreading in wireless multihop networks with churn. In: Proceedings of 6th international conference on ad hoc networks (EAI ADHOCNETS). Springer; 2014. With kind permission from Springer Science and Business Media.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 4.4. Malware Diffusion Modeling in Dynamic Networks with Churn

Create new playlist

Sign In

Sign Up

4.4. Malware Diffusion Modeling in Dynamic Networks with Churn

4.4.1. Malware Diffusion Models and Network Churn

4.4.2. Open Queuing Network Theory for Modeling Malware Spreading in Complex Networks with Churn

4.4.3. Analysis of Malware Propagation in Networks with Churn

4.4.4. Demonstration of Queuing Framework for Malware Spreading in Complex and Wireless Networks

Evaluation of malware spreading in complex networks

Evaluation of malware spreading in wireless distributed networks

Table of Contents for
4.4. Malware Diffusion Modeling in Dynamic Networks with Churn