B.5. Queues in Tandem
Realistic queuing systems are more complex than the ones presented above in Appendix B.3. However, this means that the involved analysis becomes more complex as well. This can be depicted very easily, even with the very simple queuing system of two 
queues connected in tandem, as will be shown in the sequel. Such a system is shown in Fig. B.4. The service times at the two queues are exponentially distributed and mutually independent. The queue of each system is infinite. This system can be analyzed using the methods presented previously.
queues connected in tandem, as will be shown in the sequel. Such a system is shown in Fig. B.4. The service times at the two queues are exponentially distributed and mutually independent. The queue of each system is infinite. This system can be analyzed using the methods presented previously.
Using Burke’s theorem provided above, it can be shown that the number of customers in queues 1 and 2 is independent at a given time and the stationary probability is given by
(B.14)
where 
is the traffic intensity of queues 1 and 2, respectively. The above result implies that the two queues behave as if they are independent queues. This fact comes from the assumption that the service times of a customer at the first and second queue are mutually independent as well as independent of the arrival process (Kleinrock independence approximation [25]). The proof of this result can be found in [25,142].
is the traffic intensity of queues 1 and 2, respectively. The above result implies that the two queues behave as if they are independent queues. This fact comes from the assumption that the service times of a customer at the first and second queue are mutually independent as well as independent of the arrival process (Kleinrock independence approximation [25]). The proof of this result can be found in [25,142].The above example is essentially a simple case of an acyclic (open) queuing network, where the output is not connected to the input. The routing of customers is straightforward; however, even in this case many complications might emerge. These could have significant impact on the analysis and control of such systems.
For instance, consider the degenerate case of two transmission lines of equal transmission rate in tandem (essentially the system of Fig. B.4, where there is no buffering at each queue and the service rate of each server is identical). Furthermore, assume that Poisson arrivals at rate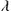 
enter the first queue and all packets have the same length (in general customers require the same service time). This means that the first queue is essentially an M/D/1 queue and the average interarrival time is given by 
, where 
and 
is the average service time [25] (the latter is a result obtained by application of the more general expression for an M/G/1 queue, but showing how to obtain this is out of the scope of this primer—the interested reader may consult [25] or other similar references to obtain the associated details). However, the interarrival times at the second queue will be greater than or equal to 
, as determined by the output of the first queue. Also, since the service times are equal at the two queues, each packet arriving at the second queue will complete service at or before the time the next packet arrives, which means there will be no queuing in the second line. Therefore, a Poisson model for the second line seems to be inappropriate even in this simple case.
enter the first queue and all packets have the same length (in general customers require the same service time). This means that the first queue is essentially an M/D/1 queue and the average interarrival time is given by , where and is the average service time [25] (the latter is a result obtained by application of the more general expression for an M/G/1 queue, but showing how to obtain this is out of the scope of this primer—the interested reader may consult [25] or other similar references to obtain the associated details). However, the interarrival times at the second queue will be greater than or equal to , as determined by the output of the first queue. Also, since the service times are equal at the two queues, each packet arriving at the second queue will complete service at or before the time the next packet arrives, which means there will be no queuing in the second line. Therefore, a Poisson model for the second line seems to be inappropriate even in this simple case.Even in the case where an queue was in the first stage, the second cannot be modeled as an as well because the interarrival times at the second queue will be strongly correlated with the packet lengths. To see this intuitively, consider a busy period of the first queue. In this case, the interarrival time of two such packets in the second queue equals the transmission time of the second packet transmitted in the first queue. This means that long packets will typically wait less at the second queue than short packets, since the second queue will have more time to empty out. Up to date there exists no analytic expression for the simple case of tandem queues shown involving Poisson arrivals and exponentially distributed services shown in Fig. B.4[25].
queue was in the first stage, the second cannot be modeled as an as well because the interarrival times at the second queue will be strongly correlated with the packet lengths. To see this intuitively, consider a busy period of the first queue. In this case, the interarrival time of two such packets in the second queue equals the transmission time of the second packet transmitted in the first queue. This means that long packets will typically wait less at the second queue than short packets, since the second queue will have more time to empty out. Up to date there exists no analytic expression for the simple case of tandem queues shown involving Poisson arrivals and exponentially distributed services shown in Fig. B.4[25]...................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.