3.3. Other Epidemics Models

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

3.3. Other Epidemics Models

The previously presented epidemics models have been mainly developed for wired networks and especially worms and viruses spreading over the Internet and exploiting elements from TCP/IP, e.g. port scanning and email attachment attacks [233]. However, epidemics models have also emerged in the literature for other types of networks, which can be physical (actual) networks of computers, e.g. local area proprietary networks, or utility grids (e.g. water pipes or electricity poles), overlay/application networks, e.g. user network of online social networks, or any other type of network representation at any intermediate protocol layer.

In the following, we present concisely some of these models for the respective network types and application scenarios. Further details for each of these approaches can be found in the corresponding bibliography provided.

3.3.1. Epidemics Model in Scale-free Networks

One of the major outcomes of epidemics is that the corresponding models, and of course the actual propagation dynamics they describe, are heavily affected by the connectivity patterns emerging in the population over which malware spreads/propagates. Simply put, connectivity affects the outcome of the propagation. Various works have identified this fact and have studied epidemics models specifically over particular network topologies. In [176], the corresponding models are studied over SF networks, which were presented in Chapter 2. The assumption is that SF networks of interest exhibit a power-law connectivity distribution

P (k) \sim k^{- γ}

$P (k) \sim k^{- γ}$

2 < γ \leq 3

$2 < γ \leq 3$

, which implies that each node-member of the population has a statistically significant probability of having a very large number of connections compared to the average connectivity

〈 k 〉

$〈 k 〉$

of the network. The employed node infection model is the SIS introduced in Section 2.3. Characteristic application scenarios considered are the Internet and maps of human sexual contacts, which in turn are characterized by SF connectivity properties. In any case, the epidemics are first developed for homogeneous networks, in terms of protocols and mixing of nodes. Homogeneous mixing means that nodes do not show special preference when interacting with each other, but rather their interactions have a more “random” nature. Then modeling is generalized to SF networks.

In one of the first analytical studies extending the SIS model over SF networks in [176], the analysis is undertaken in terms of a dynamical mean field (MF) theory [113], where average values and cumulative behavior are considered. For homogeneous networks, in which the connectivity fluctuations are very small, the MF theory is approached by means of a reaction equation for the total prevalence

ρ (t)

$ρ (t)$

, defined as the density of infected nodes present at time

t

$t$

. This reaction equation, describing the dynamics of malware diffusion, is as follows:

$\frac{d ρ (t)}{d t} = - ρ (t) + λ 〈 k 〉 ρ (t) (1 - ρ (t)) .$ $\frac{d ρ (t)}{d t} = - ρ (t) + λ 〈 k 〉 ρ (t) (1 - ρ (t)) .$

(3.18)

In the above equation,

λ = \frac{ν}{δ}

$λ = \frac{ν}{δ}$

is the effective spreading rate, where

ν

$ν$

is the probability with which each susceptible node is infected and

δ

$δ$

denotes the cure rate of infected nodes. Furthermore, the homogeneous nature of the considered network allows to use just the average connectivity

〈 k 〉

$〈 k 〉$

(as most of the probability mass for the node degrees is centered tightly around this value). By solving this equation, the main prediction of the SIS model in homogeneous networks is the presence of a positive epidemic threshold, proportional to the inverse of the average number of neighbors of every node,

〈 k 〉

$〈 k 〉$

, below which the epidemics always dies out and endemic states are impossible. Endemic states, in general, characterize cases where the malware is present in a population at consistent levels and periods of time, i.e. it does not die out, nor diffuses over the whole population. Thus, in the preceding discussion, the fact that the epidemics always dies out does not allow endemic states to emerge. The second term in the right-hand side of the above equation is denoted as “creation term.”

However, relaxing the homogeneity assumption seems oneway for modeling more accurately real networks and malware dynamics spreading over them. For this reason, the relative density

ρ_{k} (t)

$ρ_{k} (t)$

of infected nodes with given node degree

k

$k$

is employed. The dynamical mean-field equations in this case can be written as

$\frac{d ρ_{k} (t)}{d t} = - ρ_{k} (t) + λ 〈 k 〉 (1 - ρ_{k} (t)) Θ [{ρ_{k} (t)}] .$ $\frac{d ρ_{k} (t)}{d t} = - ρ_{k} (t) + λ 〈 k 〉 (1 - ρ_{k} (t)) Θ [{ρ_{k} (t)}] .$

(3.19)

The second term in the right-hand side of the above (creation term) considers the probability that a node with

k

$k$

links is healthy

(1 - ρ_{k} (t))

$(1 - ρ_{k} (t))$

and gets the infection via a connected node. The probability of this last event is proportional to the infection rate

λ

$λ$

, the real number of connections

k

$k$

, and the probability

Θ [{ρ_{k} (t)}]

$Θ [{ρ_{k} (t)}]$

that any given link points to an infected node. We make the assumption that

Θ

$Θ$

is a function of the partial densities of infected nodes

{ρ_{k} (t)}

${ρ_{k} (t)}$

. In the steady (endemic) state, the

ρ_{k}

$ρ_{k}$

are functions of

λ

$λ$

. Thus, the probability

Θ

$Θ$

becomes also an implicit function of the spreading rate, and by imposing the stationarity condition

\frac{\partial ρ_{k} (t)}{\partial t} = 0

$\frac{\partial ρ_{k} (t)}{\partial t} = 0$

, one obtains

$ρ_{k} = \frac{k λ Θ (λ)}{1 + k Θ (λ)} .$ $ρ_{k} = \frac{k λ Θ (λ)}{1 + k Θ (λ)} .$

(3.20)

With more detailed analysis that can be found in [176], an average probability of a link pointing to an infected node,

$Θ (λ) = \frac{1}{〈 k 〉} \sum_{k} k P (k) ρ_{k} .$ $Θ (λ) = \frac{1}{〈 k 〉} \sum_{k} k P (k) ρ_{k} .$

(3.21)

The analytical solutions for the Barabasi-Albert model of SF networks [1,15] can be obtained by computing the stationary points of

d ρ (t) ∕ d t = 0

$d ρ (t) ∕ d t = 0$

(Eq. (3.18)), which holds for the steady-state observation period of the system (not for the initial transient interval), yielding

$ρ [- 1 + λ 〈 k 〉 (1 - ρ)] = 0,$ $ρ [- 1 + λ 〈 k 〉 (1 - ρ)] = 0,$

which defines an epidemic threshold

λ_{c} = {〈 k 〉}^{- 1}

$λ_{c} = {〈 k 〉}^{- 1}$

and yields

•

ρ = 0

$ρ = 0$

λ < λ_{c}

$λ < λ_{c}$

•

ρ = \frac{λ - λ_{c}}{λ}

$ρ = \frac{λ - λ_{c}}{λ}$

λ \geq λ_{c}

$λ \geq λ_{c}$

Details on the analysis of real data on this model may be found in Section 1.4 of [176].

3.3.2. Generalized Epidemics-Endemics Models

The SIR epidemics model presented in Section 3.2.2 and Section 2.3 can be generalized in epidemiology to include other states that typically emerge in the cases of human virus spreading. Such states could have a notable interpretation for malware diffusion as well. In this subsection, we briefly discuss this general epidemics (or endemics) model.

The generalized epidemic model is shown in Fig. 3.6 and due to the defined succession of states, it is denoted as immunity-susceptible-exposed-infected-removed (MSEIR). The M symbol represents the state of passive immunity, namely, when a member of the population is born with antibodies, e.g. inherited by the mother or in cases of computers when the machine comes already with a patch (or service pack) preinstalled for a specific threat. Once the maternal antibodies disappear or the threat changes its parameters and the patch is not valid anymore, the corresponding member of the population transitions to the susceptible state (S), which is as described previously. Some members of the population, e.g. machines that have not preinstalled antivirus software, start from the S state. The exposed state (denoted by E) denotes cases where there exists an adequate contact of a susceptible with an infective, so that a transmission occurs between them. The following transition is to the infective state where members are capable of infecting others, and the final transition occurs toward the recovered state, where members of the population have permanent infection-acquired immunity.

In malware diffusion terminology, the passive immunity state M corresponds to machines that have been already properly patched against spreading threats. After some time, when new threats not known to manufacturers emerge, a transition to the susceptible state takes place. The exposed state E is an intermediate state that can be used to denote the state of a machine before it becomes infected. The infective and recovered states are identical to the ones defined for malware models before. This is a generalization of the node infection models presented earlier, and as mentioned already, the choice of states to include in a model depends on the characteristics of the particular malware threat or set of threats being modeled and the purpose of the model. Of course, the passively immune state M and the latent period (exposed) state E are often omitted, because they are not crucial for the SI node pair interaction, as explained in Section 2.3 in macroscopic analysis of the complex networks of interest.

One of the major features of the traditional epidemiology models is that the models for the dynamics of diffusion include both time

t

$t$

and age

a

$a$

as independent variables, because age groups mix heterogeneously, the recovered fraction usually increases with age, risks from an infection may be related to age, vaccination programs often focus on specific ages, and epidemiologic data are often age specific.

A common assumption is that the movements out of the M, E, and I states and into the next possible operational state (not the set of dead members of the population) are governed by exponentially distributed waiting times in each of the states. This assumption will be crucial in many of the more advanced techniques that will be presented in Part 2 of the book, especially in Chapter 4.

Within this framework, there are three key quantities of interest for epidemiologists that can be of particular interest to computer scientists and network engineers for the analysis and control of malware epidemics. The basic reproduction number

R_{0}

$R_{0}$

, also known as basic reproduction ratio or basic reproductive rate, is the average number of secondary infections (secondary infections refer to infections that take place by already infected legitimate nodes, not attackers themselves—primary infections) that occur when one infective is introduced into a completely susceptible host population [99]. In this definition, it is implicitly assumed that the infected outsider is in the host population for the entire infectious period and mixes with the host population in exactly the same way that a population native would mix. The contact number

σ

$σ$

is defined as the average number of adequate contacts of a typical infective during the infectious period [99]. An adequate contact is one that is sufficient for transmission, if the individual contacted by the susceptible is an infective. The replacement number

R_{p}

$R_{p}$

is defined to be the average number of secondary infections produced by a typical infective during the entire period of infectiousness [99]. All these three quantities are equal sat the beginning of the spread of an infectious disease when the entire population (except the infective invader) is susceptible.

R_{0}

$R_{0}$

is only defined at the time of invasion,

σ

$σ$

and

R_{p}

$R_{p}$

are defined at all times.

In epidemiology literature, the basic reproduction number

R_{0}

$R_{0}$

is often used as the threshold quantity that determines whether a disease can dominate over a given population or not [99]. For most models, the contact number

σ

$σ$

remains constant as the infection spreads, so it is always equal to the basic reproduction number

R_{0}

$R_{0}$

. For these cases,

σ

$σ$

and

R_{0}

$R_{0}$

can be used interchangeably. However, for other cases that new groups of infective nodes with lower infection capability appear, the contact number

σ

$σ$

for these models becomes less than the basic reproduction number

R_{0}

$R_{0}$

. The replacement number

R_{p}

$R_{p}$

is the actual number of secondary cases from a typical infective, so that after the infection has dominated a population and no one is in the susceptible state,

R_{p}

$R_{p}$

is always less than the basic reproduction number

R_{0}

$R_{0}$

. After that, the susceptible fraction is less than 1, so that not all adequate contacts result in a new infection instance. Consequently, the replacement number

R_{p}

$R_{p}$

is always less than the contact number

σ

$σ$

after the invasion. Combining these results leads to

R_{0} \geq σ \geq R_{p}

$R_{0} \geq σ \geq R_{p}$

with equality at the beginning of the attack (

t = 0, S (t) = 1

$t = 0, S (t) = 1$

, with

S (t)

$S (t)$

the fraction of the population at the susceptible state). In general,

R_{0} \geq σ

$R_{0} \geq σ$

for most models and

σ \geq R_{p}

$σ \geq R_{p}$

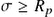after the beginning of the attack for most models.

Other epidemics models that can be derived from the aforementioned general epidemic model and have notable interest due to the various features and applications they exhibit are the following:

• The MSEIR model with exponentially changing size (churn)—The M-S-E-I-R model takes into account the fact that the population of a network changes dynamically (denoted by the term node churn), with users entering and leaving the network due to a multitude of reasons, the most prominent being the virus attack. More details and the formulation of the corresponding epidemics equations can be found in Section 3.1 of [99].

• The MSEIR model with continuous age structure—This endemic model takes into account the demographic model with continuous age (presented in Section 4.1 of [99]) and the formulation of the corresponding set of differential equations and its solution to obtain the basic reproduction number and stability properties are presented in detail in Section 5 of [99]. This model essentially takes into account the impact of aging on the members of the population and the spreading of diseases and can be extended to model the impact of user device aging patterns on malware dissemination dynamics.

• The MSEIR model with vaccination at a specific age — Such model extends the previous to the cases where vaccination (quarantine in malware terms) takes place for each population member (user). More details are provided in Section 5.5 of [99].

• The susceptible-exposed-infected-removed (SEIR) model with age groups—The S-E-I-R model utilizes the demographic model with age groups described in Section 4.2 of [99] and involves separate age groups. The formulation and solution for the basic reproduction number can be found in Section 6.1 of [99].

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 3.3. Other Epidemics Models

Create new playlist

Sign In

Sign Up

3.3. Other Epidemics Models

3.3.1. Epidemics Model in Scale-free Networks

3.3.2. Generalized Epidemics-Endemics Models

Table of Contents for
3.3. Other Epidemics Models