7.2. System Model

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

7.2. System Model

Dynamics of state evolution

A susceptible accepts a communication request with a probability

u^{N_{r}} (t)

$u^{N_{r}} (t)$

, where the subscript

r

$r$

represents reception, and the superscript

N

$N$

designates control functions of the network. At any given time

t

$t$

, there are

n_{S} (t) n_{I} (t)

$n_{S} (t) n_{I} (t)$

infective-susceptible pairs. Susceptible nodes are hence transformed to infectives at rate

\hat{β} u^{N_{r}} (t) n_{S} (t) n_{I} (t)

$\hat{β} u^{N_{r}} (t) n_{S} (t) n_{I} (t)$

, where

\hat{β}

$\hat{β}$

is the rate at which a particular pair of nodes “meet,” which is assumed to be the same for all pairs (i.e. homogeneous mixing assumption). Propagation of the worm, therefore, can be contained through appropriate regulation of

u^{N_{r}} (t)

$u^{N_{r}} (t)$

subject to

0 < u_{min}^{N_{r}} \leq u^{N_{r}} (t) \leq u_{norm}^{N_{r}} at each t

$0 < u_{min}^{N_{r}} \leq u^{N_{r}} (t) \leq u_{norm}^{N_{r}} at each t$

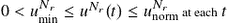. The lower bound

u_{min}^{N_{r}}

$u_{min}^{N_{r}}$

arises due to the minimum QoS requirements for data traffic, since the acceptance probability has to be the same irrespective of whether the request arrives from another infective, susceptible, or recovered node. The latter is due to the fact that a recipient node cannot distinguish the type of a transmitter in advance and has no choice but to treat all requests the same — since otherwise all infective nodes can be trivially blacklisted. The upper bound

u_{norm}^{N_{r}}

$u_{norm}^{N_{r}}$

(which can be normalized to

1

$1$

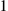) provides the reception rate that nodes use for providing the desired QoS in the absence of security considerations, i.e. during the “normal” operation of the network.

We now consider the dissemination of security patches in the network. A predetermined set of nodes, referred to as dispatchers (e.g. BS for cellular and exit-points for delay-tolerant networks), are preloaded with the patches. We assume that the dispatchers cannot be infected, and that there are

N R_{0}

$N R_{0}$

dispatchers where

N

$N$

is as usual the total number of nodes in the network and parameter

R_{0}

$R_{0}$

is between

0

$0$

and

1

$1$

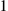. Each node communicates with the dispatchers, and thereby fetches security patches, at the overall rate of

\tilde{β} N R_{0} u^{N_{i}} (t)

$\tilde{β} N R_{0} u^{N_{i}} (t)$

at time

t

$t$

. The parameter

\tilde{β}

$\tilde{β}$

depends on node density, mobility parameters, allowable transmission rates, etc. The control function

u^{N_{i}} (t)

$u^{N_{i}} (t)$

, with subscript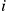

i

$i$

denoting immunization, can be used to regulate the bandwidth consumed in propagation of patches: the higher the value of

u^{N_{i}} (t)

$u^{N_{i}} (t)$

, the higher is the recovery rate but so is the rate of resource consumption in patch transmissions. Clearly, if the node that receives the patch is a susceptible node, it installs the patch and its state changes to recovered. If an infective receives the patch, the patch may fail to heal it, or, the worm may prevent its installation. We capture the above possibility, by introducing a coefficient

0 \leq π \leq 1

$0 \leq π \leq 1$

π = 0

$π = 0$

occurs when the patch is completely unable to remove the worm from infectives and only immunizes the susceptibles, whereas

π = 1

$π = 1$

represents the other extreme scenario where a patch can equally well immunize and heal susceptibles and infective nodes.¹ Now, if the patch heals an infective, its state changes to recovered, else it continues to remain an infective.

The worm at an infective host “kills” it with rate proportional to

u^{M} (t)

$u^{M} (t)$

at a given time

t

$t$

, where superscript

M

$M$

designates this is a control function of the malware; this is accomplished by executing specific codes with a probability of choice. The worm regulates the death process by appropriately choosing

u^{M} (t)

$u^{M} (t)$

at each

t

$t$

, subject to

0 \leq u^{M} (t) \leq u_{max}^{M} at each t

$0 \leq u^{M} (t) \leq u_{max}^{M} at each t$

. The upper bound arises due to processor constraints and the resulting limitations on the maximum rate of execution of such codes. Let

β_{0} : = N \hat{β}

$β_{0} : = N \hat{β}$

β_{1} : = N \tilde{β}

$β_{1} : = N \tilde{β}$

. Our discussions lead to the following system of differential equations representing the dynamics of the system:

$\dot{S} (t) = - β_{0} u^{N_{r}} I (t) S (t) - β_{1} u^{N_{i}} (t) R_{0} S (t), I (0) = lim_{N \to \infty} n_{I} (0) ∕ N = I_{0} > 0,$ $\dot{S} (t) = - β_{0} u^{N_{r}} I (t) S (t) - β_{1} u^{N_{i}} (t) R_{0} S (t), I (0) = lim_{N \to \infty} n_{I} (0) ∕ N = I_{0} > 0,$

(7.1a)

$\dot{I} (t) = β_{0} u^{N_{r}} I (t) S (t) - π β_{1} u^{N_{i}} (t) R_{0} I (t), - u^{M} (t) I (t) S (0) = 1 - I_{0},$ $\dot{I} (t) = β_{0} u^{N_{r}} I (t) S (t) - π β_{1} u^{N_{i}} (t) R_{0} I (t), - u^{M} (t) I (t) S (0) = 1 - I_{0},$

(7.1b)

$\dot{D} (t) = u^{M} (t) I (t), D (0) = 0,$ $\dot{D} (t) = u^{M} (t) I (t), D (0) = 0,$

(7.1c)

and also satisfy the following constraints at all

t

$t$

$0 \leq S (t), I (t), D (t), S (t) + I (t) + D (t) \leq 1 .$ $0 \leq S (t), I (t), D (t), S (t) + I (t) + D (t) \leq 1 .$

(7.2)

Thus,

(S (\cdot), I (\cdot), D (\cdot))

$(S (\cdot), I (\cdot), D (\cdot))$

constitute the system state functions,

u^{N} (\cdot) = (u^{N_{r}} (\cdot), u^{N_{i}} (\cdot))

$u^{N} (\cdot) = (u^{N_{r}} (\cdot), u^{N_{i}} (\cdot))$

constitutes the network control functions and

u^{M} (\cdot)

$u^{M} (\cdot)$

constitutes the malware’s control function. Note that nodes use identical reception, patching, and killing rate functions irrespective of the states in their neighborhoods since they do not know these states. Nevertheless, since these rates are allowed to vary with time, they can be chosen in accordance with how the overall network states are expected to evolve.

Henceforth, wherever not ambiguous, we drop the dependence on

t

$t$

and make it implicit. Fig. 7.1 illustrates the transitions between different states of nodes and the notations used.

Defense and attack objectives

The total damage inflicted by the malware during the network operation interval

[0, T]

$[0, T]$

is due to the presence of infectives, the death of nodes, the resources consumed for spreading the security patches, and the QoS deterioration due to the reduction of reception rate. Infectives can perform harmful activities over time. Dead nodes are inoperative and thus inflict a time-accumulative cost on the network. The bandwidth overhead at time

t

$t$

due to the media scanning and transmission of the security packets by the dispatchers is

R_{0} u^{N_{i}} (t)

$R_{0} u^{N_{i}} (t)$

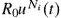. Due to the reception rate control, the susceptibles lose a

1 - u^{N_{r}} (t) ∕ u_{norm}^{N_{r}}

$1 - u^{N_{r}} (t) ∕ u_{norm}^{N_{r}}$

fraction of packets transmitted by all nodes which degrades the overall QoS. We therefore consider the aggregate network damage at time

t

$t$

as a combination of

I (t), D (t), u^{N_{i}} (t), u^{N_{r}} (t)

$I (t), D (t), u^{N_{i}} (t), u^{N_{r}} (t)$

. We adopt a linear cost function in this chapter for analytical tractability. Note that the damage function can be scaled so that one of the coefficients may be chosen as unity: we choose the one associated with the instantaneous bandwidth overhead. Thus, the damage over the interval

[0, T]

$[0, T]$

is²

$J (u^{N} (t), u^{M} (t)) = \int_{0}^{T} [κ_{I} I (t) + κ_{D} D (t) + R_{0} u^{N_{i}} (t) - κ_{r} u^{N_{r}} (t)] d t + K_{D} D (T),$ $J (u^{N} (t), u^{M} (t)) = \int_{0}^{T} [κ_{I} I (t) + κ_{D} D (t) + R_{0} u^{N_{i}} (t) - κ_{r} u^{N_{r}} (t)] d t + K_{D} D (T),$

(7.3)

where

K_{D} D (T)

$K_{D} D (T)$

relates to the final tally of the dead nodes. The coefficients are all non-negative and represent the relative importance of each corresponding term in the overall damage, e.g. if the worm gains the most by killing, and thereby completely disabling nodes,

κ_{D} > > κ_{I}

$κ_{D} > > κ_{I}$

. Let

κ_{I} > 0, κ_{r} > 0

$κ_{I} > 0, κ_{r} > 0$

The network seeks to choose its control vector

u^{N} (\cdot)

$u^{N} (\cdot)$

so as to minimize the above while the malware seeks to choose its control

u^{M} (\cdot)

$u^{M} (\cdot)$

so as to maximize the above, subject to satisfying state constraints (7.2) and ensuring that

$u_{min}^{N_{r}} \leq u^{N_{r}} (t) \leq u_{norm}^{N_{r}}, 0 \leq u^{N_{i}} (t) \leq 1,$ $u_{min}^{N_{r}} \leq u^{N_{r}} (t) \leq u_{norm}^{N_{r}}, 0 \leq u^{N_{i}} (t) \leq 1,$

(7.4a)

$0 \leq u^{M} (t) \leq u_{max}^{M} .$ $0 \leq u^{M} (t) \leq u_{max}^{M} .$

(7.4b)

In Section 7.3, we model their interactions resulting from opposing objectives as a dynamic game. The formulation relies on the following result that allows us to ignore the state constraints without any loss of generality. The proof is similar to that of Lemma 6.1 in the previous chapter and is hence omitted for brevity.

Lemma 7.1

Any pair of strategies

(u^{N} (\cdot), u^{M} (\cdot))

$(u^{N} (\cdot), u^{M} (\cdot))$

that satisfy the control constraints(7.4a),(7.4b), satisfy state constraints(7.2)and further ensure that

I (t) > 0, S (t) > 0

$I (t) > 0, S (t) > 0$

for all

t \in [0, T]

$t \in [0, T]$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 7.2. System Model

Create new playlist

Sign In

Sign Up

7.2. System Model

Dynamics of state evolution

Defense and attack objectives

Table of Contents for
7.2. System Model