B.2. Basic Queuing Systems, Notation, and Little’s Law

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

B.2. Basic Queuing Systems, Notation, and Little’s Law

In this section, we start by introducing the components of a queuing system, and then explain the employed notation. Then, fundamental stochastic processes and simple but useful results, e.g. Little’s law, are presented.

B.2.1. Elements of a Queuing System

The simplest queuing system is shown in Fig. B.1. It consists of two distinct components, namely, a generic queue (buffer space) and a generic server. The queue/buffer provides storage space for the customers that enter the system and cannot be served immediately (delayed in the system), while the server corresponds to the processing (service) required by each customer. For example, if customers correspond to network packets, the processing can be the time required to determine routing and transmit packets, etc. In the instance shown in Fig. B.1, the queue is considered discrete, e.g. it accommodates humans in a bank queue, packets in a communications network, as opposed to a continuous queue. An example of the latter is a communications network, where one would treat the information content of the packets as a continuous quantity, e.g. liquid and draw an analogy between a router and a water dam, where water corresponds to information content and the dam valve to the router processor. In that sense, the continuous queue is an idealization of the actual queue, since in nature all quantities emerge discrete, which is used for mathematical tractability.

Consequently, each queuing system consists of a waiting component and a serving component, as well as a generic input (arrival) and generic output (service) streams. Multiple input/output streams might be implemented in real systems, both of which are typically of stochastic nature, i.e. proper stochastic processes [187].

The service discipline of a system determines the output. Together with the buffering discipline, which partially determines the time a customer spends in the system, the arrival and service processes are critical for the evolution and behavior of the queuing system. For the simple but generic system shown in Fig. B.1, the queuing time and the service time of each customer determine the total time spent by the customer in the system. The arrival process is characterized by the times between two successive arrivals (interarrival times) and the service process by the times between two successive services (service times) . In simple queuing systems, successive services are independent of each other and independent of the sequence of interarrival times, while in more complex ones this is not the case [25,142,229].

The service and queuing disciplines can vary considerably. For instance, with reference to Fig. B.1, the simplest queuing discipline is the first-in-first-out (FIFO) [25,33,211], where arriving customers always enter the queue before being served, while a customer is removed from the queue and assigned to the server when the latter becomes free, according to a specific policy. In FIFO, customers enter the queue sequentially (queuing policy) and served (service policy) at the same order. Other similar disciplines like last-in-first-out (LIFO or commonly known as stack), heap implementing queuing with priorities (analyzed in detail in Section 3.5.3 of [25]), etc., might be applied and considered, and for more details the interested reader may find more details in [25,33,211]. The above disciplines are work-conserving, meaning that if one customer is served, the next in queue will take its place. Hence, the serving policy will prevent the system from becoming idle, if customers (work) still remain in the system (in queue). Queuing behavior can also depend on different queuing/serving policies determined by priorities, fairness factors, etc. More details are out of scope of this primer and can be found in relevant references [25,33,36,90,142,209,211,229].

B.2.2. Fundamental Notation and Quantities of Interest

In order to characterize queuing systems, a notation system has been proposed by Kendall in 1951 and it was adopted by the research and industrial communities. A three or four part symbol is used in the form of

X ∕ Y ∕ z ∕ w

$X ∕ Y ∕ z ∕ w$

, where

X

$X$

specifies the stochastic input process (interarrival distribution),

Y

$Y$

specifies the service policy (service time distribution defined by the corresponding stochastic process),

z

$z$

denotes the number of servers, and

w

$w$

specifies the total holding capacity of the system including any served customers, if any. Table B.1 summarizes the most frequently used symbol used to explicitly denote the input/service processes (time interval distribution between successive arrivals or services) in Kendall notation. Symbol “

M

$M$

” stands for Poisson or exponential process (memoryless/Markovian), symbol “

D

$D$

” for deterministic arrival/service disciplines, “

E_{n}

$E_{n}$

” represents Erlangian distribution policies, “

G

$G$

” for an arbitrary distribution function, and “

G I

$G I$

” for general but independent distribution policies. Thus, for example, a

M ∕ M ∕ 2

$M ∕ M ∕ 2$

notation defines a queuing system with two servers with common queue of infinite capacity, Poisson arrivals, and exponential service times, while

M ∕ M ∕ 2 ∕ 4

$M ∕ M ∕ 2 ∕ 4$

defines a similar system, where the buffer holds only two incoming customers, discarding any excess arrivals. This is a system of maximum capacity four, two customers at service and two waiting in the best case. A fifth customer will be discarded as opposed to an

M ∕ M ∕ 2

$M ∕ M ∕ 2$

system.

Table B.1

Arrival-Service Discipline Characterization in Kendall Notation

Symbol	Meaning
$M$ $M$	Poisson or exponential (Markovian/memoryless)
$D$ $D$	Deterministic
$E_{n}$ $E_{n}$	Erlangian distribution
$Geom$ $Geom$	Geometric distribution
$G$ $G$	Arbitrary distribution function
$G I$ $G I$	Arbitrary independent distribution function

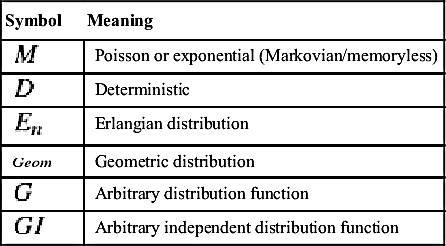
In general, it should be pointed that interarrival and service times in systems typically described by Kendall notation are assumed independent of each other and in addition identically distributed (interarrival times and service times separately). This is usually denoted as “i.i.d.” Of course, the distribution of interarrival times may be different than that of service times, as explained above.

In many cases, it is possible to analytically study queuing systems of interest. When analyzing such queuing systems, the most important quantities of interest for identifying the key factors and assessing the performance of the corresponding system are summarized in the following list:

• The average number of customers in the buffer (queue) space,

• the average total number of customers in the system (queue and server),

• the average waiting time for a customer (expected time spent in the queue only),

• the average system time (expected total time spent in the system),

• the average busy period time (expected time the server works before becoming idle),

• the average system throughput (number of successfully served customers in the time unit).

In real complex systems, it is typically tough to obtain analytic expressions for quantities as the ones mentioned above. However, in some simple yet useful systems, it is possible to obtain such expressions and study explicitly the behavior of their evolution, as shown for some of them in Appendix B.3. Building suitable approximations allows the analysis and study of even more these complex queuing systems, as can be seen in more dedicated treatments of the topic [25,36,209,229].

B.2.3. Relation Between Arrival-Departure Processes and Little’s Law

Both arrival and departure processes of a queuing system are associated with two corresponding counting processes, the first counting the number of arriving customers and the second counting the departed customers (those that finished waiting and service and leaving the system completely). The difference between the arrival and departing counting processes yields the number of customers currently in the system (waiting and served cumulatively). If

a (t)

$a (t)$

is the arrival and

b (t)

$b (t)$

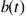the departure counting process, respectively, then

N (t) = a (t) - b (t)

$N (t) = a (t) - b (t)$

is the number of customers in the system, assuming the system starts empty. Fig. B.2 shows an instance of such counting processes for the evolution of a queuing system with a FIFO discipline over time in the time interval

[0, t]

$[0, t]$

. If

T_{i}

$T_{i}$

represents the time spent in the system by customer

i

$i$

, the area between the two curves is given by

\int_{0}^{t} N (τ) d τ = \sum_{i = 1}^{α (t)} T_{i}

$\int_{0}^{t} N (τ) d τ = \sum_{i = 1}^{α (t)} T_{i}$

. Dividing this by

t

$t$

and taking the limit as

t

$t$

tends to

\infty

$\infty$

Fig. B.2 — FIGURE B.2 Graphical presentation of the relation between the arrival-departure counting processes and visual explanation of Little’s law.

$\frac{1}{t} \int_{0}^{t} N (τ) d τ = \frac{1}{t} \sum_{i = 1}^{α (t)} T_{i} = \frac{α (t)}{t} \frac{\sum_{i = 1}^{α (t)} T_{i}}{α (t)}$ $\frac{1}{t} \int_{0}^{t} N (τ) d τ = \frac{1}{t} \sum_{i = 1}^{α (t)} T_{i} = \frac{α (t)}{t} \frac{\sum_{i = 1}^{α (t)} T_{i}}{α (t)}$

yields a very important result, most widely known as Little’s law.

Theorem B.1

Little’s Law

N

$N$

is the average number of customers in the system,

λ

$λ$

the mean arrival rate, and

T

$T$

the mean system time, these are related with the simple formula

$N = λ T .$ $N = λ T .$

(B.1)

It should be highlighted that the terms “averages” in Little’s law are long-term time averages, which for a stationary system these averages are also equal to the expected values of the corresponding random variables.

Even though a proof can be found in [25], Little’s law does not qualify for a formal mathematical theorem, since it essentially expresses a conservation principle with respect to the customers of a queuing system. Little’s law expresses the intuitive idea that the number of customers in the system depends on the average delay and vice versa. This is intuitively justified if one considers that in each queuing system that does not absorb customers, i.e. all customers entering the system will eventually depart, the more customers enter in the system, the more the average delay experienced by a random customer will be and vice versa, i.e. the more the average delay experienced by an individual customer, the more customers are expected to be found in the system. The relation between the expected number of customers and the average delay of a customer is given by Little’s law. Little’s law is used extensively in Chapter 4 for relating the expected number of infected nodes with the expected time these nodes remain in the infected state under the SIS infection model. Essentially, the expected infection duration can be obtained in each scenario via Little’s law.

Although it looks intuitively reasonable, it is quite a remarkable result, as the corresponding relationship it expresses is not influenced by the arrival process distribution, the service distribution, the service order, or practically anything else. In addition, Little’s law has more general value and can be applied recursively to arbitrary components of a queuing system, i.e. in systems within systems. For instance, if only the queue is considered,

N_{Q} = λ W

$N_{Q} = λ W$

gives the number of customers in the queue as a function of the arrival rate (in the queue) and the mean waiting time

W

$W$

. The only requirements are that the system is stable and non-preemptive, thus ruling out transition states such as initial startup or shutdown transient phenomena. If the system has

n

$n$

different inputs, each with rate

λ_{i}

$λ_{i}$

, then Little’s theorem yields

N = \sum_{i = 1}^{n} λ_{i} T

$N = \sum_{i = 1}^{n} λ_{i} T$

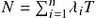..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for B.2. Basic Queuing Systems, Notation, and Little’s Law

Create new playlist

Sign In

Sign Up

B.2. Basic Queuing Systems, Notation, and Little’s Law

B.2.1. Elements of a Queuing System

B.2.2. Fundamental Notation and Quantities of Interest

B.2.3. Relation Between Arrival-Departure Processes and Little’s Law

Table of Contents for
B.2. Basic Queuing Systems, Notation, and Little’s Law