Chapter 7

Conditional Power in Clinical Trial Monitoring

Ming T. Tan

7.1 Introduction

For ethical, economical, and scientific reasons, clinical trials may be terminated early for a pronounced treatment benefit or the lack thereof. In addition to group sequential tests and type I error-spending functions, another approach is to address the question more directly by asking whether the accumulated evidence is sufficiently convincing for efficacy. Or, if evidence is lacking, one should ask whether the trial should continue to the planned end and whether the conventional (reference) nonsequential test (RNST) should be employed. Conditional power is one way to quantify this evidence. It is simply the usual statistical power of RNST conditional on the current data. Thus, it is the conditional probability that the RNST will reject the null hypothesis on completion of the trial given the data currently available at a given parameter value of the alternative hypothesis. Therefore, if the conditional power is too low or exceedingly high, then the trial may be terminated early for futility or for efficacy, respectively. The early stopping procedure derived based on conditional power is referred to as stochastic curtailing, by which an ongoing trial is curtailed as soon as the trend based on current data becomes highly convincing [1]. Therefore, conditional power serves two closely related purposes: (1) as a measure of trend reversal (e.g., futility index) and (2) as an interim analysis procedure (e.g., formally a group sequential method). This method can be readily communicated to nonstatisticians because it simply answers the question of whether the evidence in the interim data is sufficient for making an early decision on treatment efficacy or the lack thereof given current data in reference to what the RNST concludes.

7.2 Conditional Power

To introduce the concept with statistical rigor and clarity, we consider the statistical framework of testing a normal mean into which many clinical trials can be formulated [2,3]. We have H₀: μ = 0 versus the alternative H₁: μ > 0, where μ denotes the treatment effect parameter and (for example) is the mean elevation of diastolic blood pressure above 90 mmHg. Let m be the maximum sample size of the RNST and the current data be S_n. Then the conditional power is defined as

Furthermore, let X_i be the observed elevation of diastolic blood pressure above 90 mmHg of the ith subject. Thus, X_i ~ (μ, σ²), i = 1, · · ·, n, · · ·, m. Then the current data are summarized by the sufficient statistic, the partial sum S_n = Σ_i=1ⁿ X_i. Then S_n ~ N(nμ, nσ²), n = 1, · · ·, m, where it is assumed that σ = 28.3 mmHg based on preliminary data. We are interested in detecting a clinically important difference of 10 mmHg at a significance level of α (for example, 0.025) with power 1 − β (for example, 0.90). The fixed sample design requires m = 86 subjects, and the null hypothesis would be rejected if Z_m > Z_α = 1.96, where Z_m = and z_α is the lower α-percentile of the standard normal curve, or equivalently S_m > s₀, where s₀ = = 554.68. Therefore, the conditional power is evaluated under the following conditional distribution:

(1)

and thus it is given by

A similar derivation for two-sided tests can be found in Reference 3. Because the conditional power depends on the unknown true treatment effect parameter μ, different hypothetical values of μ have to be given to evaluate the conditional power. A common practice is to consider three values: the null value, the value under the alternative hypothesis that the study is designed to detect, and the current estimate. One such current value is the average of the null and the alternative. If in the midcourse (n = 43), the average elevation of blood pressure (xbar in Figure 1) is 8 mmHg (i.e., S_n = 43 * 8 = 344) and the true treatment effect μ is 10 mmHg, then the conditional power is 92%, which implies there is a good chance the null hypothesis will be rejected at the planned end of the trial. On the other hand, if the average elevation is 2, then the conditional power is only 49%. The conditional power has been used more often as a futility index. If the conditional power at the alternative hypothesis is too low (for example, less than 0.20), then the trial is not likely to reach statistical significance and achieve its original goal of detecting a treatment improvement, which provides an argument for early termination of the trial for futility. Figure 1 gives the usual power function of the test as well as the conditional power that corresponds to the two average elevations of blood pressures (xbar values) at midcourse (n = 43) of the trial. Figure 2 gives the stochastic curtailing boundaries based on the conditional power.

Figure 1: Illustration of the conditional power

Figure 2: Stopping boundaries of different stochastic curtailing procedures (DP denotes discordance probability)

The difficulty is at which μ the conditional power should be evaluated because it may be hard to anticipate a future trend. A stochastic curtailing procedure can be derived using the conditional power of the RNST given S_n and some plausible values of the treatment effects. Then, we can derive a formal sequential test with upper boundary a_n and lower boundary b_n where we reject H₀ the first time Z_n ≥ a_n or accept H₀ the first time Z_n ≤ b_n. If the conditional power at μ = 0 is greater than γ₀ (for example, 0.80), then H₀ is rejected, and if the conditional power at μ = 10 is less than 1 − γ₁ (for example, 0.20), then H₁ is accepted. Then, the sequential boundaries are and . It can be shown [1] that the derived curtailing procedure has a type I error no greater than α/γ₀ (0.0625) and type II error no greater than β/γ₁ (0.25). Figure 2 gives the boundaries of the two stochastic curtailing procedures based on conditional power with γ₀ = γ₁ = γ = 0.80 and 0.98. The extreme early conservatism of stochastic curtailing is apparent.

It is now well known and widely utilized in the monitoring of clinical trials that the test statistic in most of the common phase III clinical trials can be formulated into the general Brownian motion framework [4]. In other words, the test statistic can be generally rescaled into a normalized statistic B_t = Z_n (0 ≤ t ≤ 1) that follows approximately a Brownian motion with drift parameter μ. Thus μ may represent the pre-post change, or a log odds ratio or a log hazard ratio. The primary goal is to test H₀: μ = 0 versus the alternative H₁: μ > 0. Then, the conditional distribution of B₁ given B_t is again normal with mean B_t + (1 − t)μ and variance 1 − t. Therefore, the conditional power in the general Brownian motion formulation is

For a two-sided test, the conditional power is given by

Several authors [3–5] have documented in detail how to formulate common clinical trials with various types of end points into the Brownian motion framework. For example, the sequentially computed log-rank statistic is normally distributed asymptotically with an independent increment structure [6,7]. The conditional power is given in Reference 8 for comparing two proportions, in Reference 9 for censored survival time for log-rank or weighted log-rank statistics, in Reference 10 for longitudinal studies, and in Reference 11 for models with covariates. In addition, several authors have used conditional power as an aid to extend an ongoing clinical trial to beyond the originally planned end for survival outcome [12] and in Brownian motion [13]. More recently, the discordance probability (to be introduced in Section 7.4) is also extended and derived under the general Brownian motion framework [14,15]

7.3 Weight-Averaged Conditional Power or Bayesian Predictive Power

Another way to avoid explicit choices of the unknown parameter is to use the weighted average of the conditional power with weights given by the posterior distribution of the unknown parameter μ given currently available data. Let the prior distribution of μ be π(μ) and its posterior be π(μ|S_n). Then, the weight-averaged conditional power (also known as predictive power) for the one-sided hypothesis testing is given by

If the improper as well as noninformative prior π(μ) = 1 is chosen, then the posterior of μ|S_n is normal with mean S_n/n and variance σ²/n. Then from Equation (1), the marginal distribution of S_m|S_n is again normal with mean (m/n)S_n and variance σ²((m − n)m/n). The predictive power is thus simply:

Several authors have used the predictive power approach [16–18]. Similar to conditional power, if P_n ≥ γ₀, we consider rejecting the null, and if P_n ≤ 1 − γ₁, we consider accepting the null. This criterion results in the following interim analysis procedure with boundaries and . Unfortunately, no simple relationship exists to relate the type I and II errors of the procedure with the predictive power. However, more informative usage of the predictive power may be through an informative prior. The data monitoring committee can make full use of the predictive power to explore the consequences of various prior beliefs on the unknown treatment effect parameter.

7.4 Conditional Power of a Different Kind: Discordance Probability

Based on the same principle of stopping a trial early as soon as the trend becomes inevitable, it is revealing to consider the conditional likelihood of the interim data given the reference test statistic at the planned end of the trial (m):

The distinct advantage of using this conditional likelihood approach is that it does not depend on the unknown parameter μ because conditioning is made on S_m, which is a sufficient statistic for μ.

Using this conditional likelihood of the test statistic calculated at an interim time, we can derive a different kind of stochastic curtailing based on discordance probability defined as the probability that the sequential test does not agree with the RNST in terms of accepting or rejecting the nail hypothesis should the trial continue to the planned end (m). At a given interim time point n, let a_n be the upper (rejection) boundary (i.e., if S_n ≥ a_n, reject the null hypothesis). Then P_μ (S_n ≥ a_n|S_m ≤ s₀) is the probability that the decision to reject H₀ at n with S_n ≥ a_n is discordant with the decision to accept H₀ at m when S_m ≤ s₀. In simple words, this kind of conditional power or reverse curtailing is derived from the likelihood function given the eventuality. Because for any μ,

we can use P(S_n ≥ a_n|S_m = s₀) to derive a sequential boundary. If this probability is smaller than ξ, then we stop the test and reject the null hypothesis, and, similarly, if P(S_n ≤ b_n|S_m = s₀) < ξ, then we stop the test and do not reject the null hypothesis. If we choose ξ(say, 0.05), that is, the same cutoff point for each n (n = 1, · · ·, m), then we have

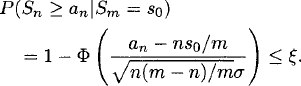
Solving this equation we have and . It is worth noting again that the boundaries are derived using marginal probability ξ for each n(n = 1, · · ·, m). Marginally, the stopping boundaries are the same as those from predictive power with noninformative prior. A more accurate statement may be by a global discordance probability defined as the probability that the sequential test on interim data does not agree with the acceptance/rejection conclusion of the RNST at the planned end [19]. Xiong [19] derived the elegant sequential conditional probability ratio test (SCPRT) via a conditional likelihood ratio approach and obtained the boundaries of the same form. Most importantly, he derived the intricate relationship among the type I, II errors, the discordance probability, and he developed an efficient algorithm to compute them. In addition, he shows that the sequential boundary can be derived such as it has virtually the same type I and II errors as the RNST and the probability that the rejection or acceptance of the null hypothesis based on interim data might be reversed is less than a given level ρ₀ (for example, 0,02) should the trial continue to the planned end. With instantaneous computation of the type I and II errors and various discordance probabilities, a sharper monitoring boundary can be derived [14,19–22]. Such superefficiency under all the constraints is the clear advantage of the SCPRT. It is noted that similar boundaries themselves have also been derived for Bernoulli series using this stochastic curtailing approach in the context of reducing computation in a simulation study designed to evaluate the error rates of a bootstrap test [23].

Figure 2 also gives the boundaries of the stochastic curtailing procedure based on the discordance probability with a maximum discordance probability (denoted DP in Figure 2) less than 0.02. In contrast to the extreme early conservatism of stochastic curtailing based on conditional power, the three boundaries become closer as the trial approaches its end. Interestingly, in the last quarter of the information fraction of the trial, the curtailing procedure (with γ = 0.98) almost coincides with that of the SCPRT, whereas the boundary with γ = 0.80 becomes slightly tighter than that of the SCPRT. which results in an increase in discordance probability relative to that of the RNST, reflecting the conservatism in the SCPRT. A more detailed comparison of the two curtailing approaches and the SCPRT with common group sequential procedures such as the O’Brien-Fleming, Pocock, and Haybittle–Peto procedures is given in References 21 and 22.

7.5 Analysis of a Randomized Trial

The Beta-Blocker Heart Attack Trial was a randomized double-blind trial to compare propranolol (n = 1916) with placebo (n = 1921) in patients who had recent myocardial infarction sponsored by the National Institutes of Health. Patients were accrued from June 1978 to June 1980 with a 2-year follow-up period resulting in a 4-year maximum duration. The trial was terminated early for a pronounced treatment benefit. Aspects on the interim monitoring and early stopping of this trial have been summarized [24–26]. The minimum difference of clinical importance to be detected is 0.26 in log hazard ratio derived based on projected 3-year mortality rates of 0.1746 for the placebo group and 0.1375 for the treatment group adjusting for compliance. Roughly 628 deaths are required for a fixed sample size test to detect such a difference at a significance level of 5% with 90% power. Seven interim analyses that correspond to the times the Policy and Data Monitoring Board met were planned. The trial was stopped 9 months early at the sixth interim analysis with 318 deaths (183 in the placebo arm and 125 in the treatment arm) with the standardized z-statistic valued at 2.82, and the O’Brien-Fleming boundary was crossed.

The conditional power can be evaluated for various expected deaths. For example, a linear interpolation of the life table based on the current survival data suggests 80 additional deaths in the ensuing 9 months. Therefore, the information time at the sixth analysis is 318/(318 + 80) = 0.80, then B_t = 2.82 = 2.52. The conditional power p_0.80(0) is 0.89. If an additional 90 deaths are expected, then the conditional power p_0.78(0) is 0.87. Both suggest a rather high conditional power for a treatment effect. Assuming an additional 90 deaths, the SCPRT curtailing based on discordance probability can be derived [14], which gives a maximum discordance probability of 0.001. This finding implies that there is only 0.1% chance that the conclusion might be reversed had the trial continued to the planned end [14]. If the 628 total deaths in the original design are used, and should an SCPRT procedure be in place (stated in the protocol), then the maximum discordant probability would be 1%, which implies only a slight chance (1%) that the decision based on the SCPRT procedure in the protocol might be reversed had the trial continued to the planned end [21]. Therefore, it is highly unlikely that the early stopping decision for efficacy by all three procedures would be reversed had the trial continued to the planned end. However, the SCPRT -based curtailing provides a sharper stopping boundary for trend reversal as expected and thus stronger confidence in the conclusion.

7.6 Conditional Power: Pros and Cons

To put things in perspective, the conditional power approach attempts to assess whether evidence for efficacy or the lack of it based on the interim data is consistent with that at the planned end of the trial by projecting forward or using conditional likelihood given the eventuality. Thus, it substantially alleviates the major inconsistency in all other group sequential tests where different sequential procedures applied to the same data yield different answers. This inconsistency with the nonsequential test sets up a communication barrier in practice where we can claim a significant treatment effect via the nonsequential test but cannot to do so via the sequential test based on the same data set or we can claim significance with one sequential method but cannot do so with another. For example, in a clinical trial that compares two treatments at the 5% significance level where five interim analyses were planned, the nominal level at the fifth analysis for the Petcock procedure is 0.016 whereas the nominal level at the fifth interim analysis for the O’Brien-Fleming procedure is 0.041. If the trial has a nominal P-value of 0.045 at the fifth analysis, then according to either of the group sequential designs, the treatment effect would not be significant, whereas investigators with the same data just carrying out a fixed sample size test would claim a significant difference. However, if the nominal P-value is 0.03, then the treatment effect is significant according to the O’Brien-Fleming procedure but not according to the Pocock procedure.

The advantage of the conditional power approach for trial monitoring is its flexibility. It can be used for unplanned analysis and even analyses whose timing depends on previous data. For example, it allows inferences from overrunning or underrunning (namely, more data come in after the sequential boundary is crossed, or the trial is stopped before the stopping boundary is reached). Conditional power can be used to aid the decision for early termination of a clinical trial to complement the use of other methods or when other methods are not applicable. However, such flexibility comes with a price: potentially more conservative type I and type II error bounds (α/γ₀ and β/γ₁) that one can report. The SCPRT-based approach removes the unnecessary conservatism of the conditional power and can retain virtually the same type I and II errors with a negligible discordance probability by accounting for how the data pattern (sample path) is trended (traversed). The use of the SCPRT especially in making decisions in early stages has been explored by Freidlin et al. [27] and for one-sided tests by Moser and George [28]. The greatest advantage of predictive power is that it allows us to explore consequences of various prior beliefs about the unknown treatment effect parameter. Finally, conditional power has also been used to derive tests adaptive to the data in the first stage of the trial (see Reference 13), More recently, the related reverse stochastic curtailing and the discordance probability have been used to derive group tests adaptive to updated estimates of the nuisance parameter [14].

References

[1] K. Lan, R. Simon, and M. Halperin, Stochastically curtailed tests in long-term clinical trials. Sequent. Anal. 1982; 1: 207–219.

[2] J. Whitehead, A unified theory for sequential clinical trials. Stat. Med. 1999: 2271–2286.

[3] C. Jennison and B. W. Turnbull, Group Sequential Methods with Applications to Clinical Trials. New York: Chapman & Hall/CRC, 2000.

[4] K. K. Lan and D. M. Zucker, Sequential monitoring of clinical trials: the role of information and Brownian motion. Stat. Med. 1993; 12: 753–765.

[5] J. Whitehead, Sequential methods based on the boundaries approach for the clinical comparison of survival times. Stat. Med. 1994; 13: 1357–1368.

[6] M. H. Gail, D. L. DeMets, and E. V. Slud, Simulation studies on increments of the two-sample logrank score test for survival time data, with application to group sequential boundaries. In: J. Crowley and R. A. Johnson (eds.), Survival Analysis. Hayward, CA: Instititute of Mathematical Statistics, 1982, pp. 287–301.

[7] A. A. Tsiatis, Repeated significance testing for a general class of statistics used in censored survival analysis. J. Am. Stat. Assoc. 1982; 77: 855–861.

[8] M. Halperin, K. K. Lan, J. H. Ware, N. J. Johnson, and D. L. DeMets, An aid to data monitoring in long-term clinical trials. Control. Clin. Trials 1982; 3: 311–323.

[9] D. Y. Lin, Q. Yao, Z. Ying, A general theory on stochastic curtailment for censored survival data. J. Am. Stat. Assoc. 1999; 94: 510–521.

[10] M. Halperin, K. K. Lan, E. C. Wright, and M. A, Foulkes, Stochastic curtailing for comparison of slopes in longitudinal studies. Control. Clin. Trials 1987; 8: 315–326.

[11] C. Jennison and B. W. Turnbull, Group-sequential analysis incorporating covariate information. J. Am. Stat. Assoc. 1997: 92: 1330–1341.

[12] P. K. Andersen, Conditional power calculations as an aid in the decision whether to continue a clinical trial. Control. Clin. Trials 1986; 8: 67–74.

[13] M. A, Proschan and S. A. Hunsberger, Designed extension of studies based on conditional power. Biometrics 1995: 51: 1315–1324.

[14] X. Xiong, M. Tan, and J. Boyett, Sequential conditional probability ratio tests for normalized test statistic on information time. Biometrics 2003; 59: 624–631.

[15] X. Xiong, M. Tan, and J. Boyett, A sequential procedure for monitoring clinical trials against historical controls. Stat. Med. 2007; 26: 1497–1511.

[16] J. Herson, Predictive probability early termination plans for phase II clinical trials. Biometrics 1979; 35: 775–783.

[17] S. C. Choi, P. J. Smith, and D. P. Becker, Early decision in clinical trials when the treatment differences are small. Experience of a controlled trial in head trauma. Control. Clin. Trials 1985; 6: 280–288.

[18] D. J. Spiegelhalter, L. S. Freedman, and P. R. Blackburn. Monitoring clinical trials: Conditional or predictive power? Control. Clin. Trials 1986; 7: 8–17.

[19] X. Xiong, A class of sequential conditional probability ratio tests. J. Am. Stat. Assoc. 1995; 90: 1463–1473.

[20] X. Xiong, M. Tan, M. H. Kutner, Computational methods for evaluating sequential tests and post-test estimation via the sufficiency principle. Statist. Sin. 2002; 12: 1027–1041.

[21] M. Tan, X. Xiong, M. H. Kutner, Clinical trial designs based on sequential conditional probability ratio tests and reverse stochastic curtailing. Biometrics 1998; 54: 682–695.

[22] M. Tan and X. Xiong, Continuous and group sequential conditional probability ratio tests for phase II clinical trials. Stat. Med. 1996; 15: 2037–2051.

[23] C. Jennison, Bootstrap tests and confidence intervals for a hazard ratio when the number of observed failures is small, with applications to group sequential survival studies. In: C. Page and R. LePage (eds.), Computing Science and Statistics: Twenty-second Symposium on the Interface. Berlin: Springer-Verlag, 1992, pp. 89–97.

[24] D. L. DeMets and K. K. Lan, Interim analysis: the alpha spending function approach. Stat. Med. 1994; 13: 1341–1352; discussion 1353–1356.

[25] D. L. DeMets, R. Hardy, L. M. Friedman, and K. K. Lan, Statistical aspects of early termination in the beta-blocker heart attack trial. Control. Clin. Trials 1984; 5: 362–372.

[26] K. K. Lan and D. L. DeMets, Changing frequency of interim analysis in sequential monitoring. Biometrics 1989; 45: 1018–1020.

[27] B. Freidlin, E. L. Korn, and S. L. George, Data monitoring committees and interim monitoring guidelines. Control. Clin. Trials 1999; 20: 395–407.

[28] B. K. Moser and S. L. George, A general formulation for a one-sided group sequential design. Clin. Trials 2005; 2: 519.