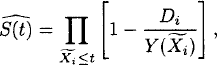Chapter 50

Survival Analysis, Overview

Per Kragh Andersen and Niels Keiding

50.1 Introduction

Survival analysis is the study of the distribution of lifetimes, that is, the times from an initiating event (birth, start of treatment, employment in a given job) to some terminal event (death, relapse, disability pension). A distinguishing feature of survival data is the inevitable presence of incomplete observations, particularly when the terminal event for some individuals is not observed; instead, it is only known that this event is at least later than a given point in time: right censoring.

The aims of this entry are to provide a brief historical sketch of the long development of survival analysis and to survey what we have found to be central issues in the current methodology of survival analysis. Necessarily, this entry is rich in cross-references to other entries that treat specific subjects in more detail. However, we have not attempted to include cross-references to all specific entries within survival analysis.

50.2 History

50.2.1 The Prehistory of Survival Analysis in Demography and Actuarial Science

Survival analysis is one of the oldest statistical disciplines, with roots in demography and actuarial science in the seventeenth century; see References 49 (Chapter 2) and 51 for general accounts of the history of vital statistics and Reference 22 for specific accounts of the work before 1750.

The basic life table methodology in modern terminology amounts to the estimation of a survival function (1 minus distribution function) from lifetimes with delayed entry (or left truncation; see below) and right censoring. This was known before 1700 and explicit parametric models at least since the linear approximation of de Moivre [39] [see, e.g., Reference 22, p. 517], later examples being due to Lambert [33, p. 483]:

(1)

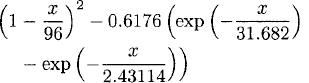
and the influential nineteenth-century proposals by Gompertz [19] and Makeham [37], who modeled the hazard function as bc^x and a + bc^x, respectively.

Motivated by the controversy over smallpox inoculation, D. Bernoulli [5] laid the foundation of the theory of competing risks; see Reference 44 for a historical account. The calculation of the expected number of deaths (how many deaths there would have been in a study population if a given standard set of death rates applied) also dates back to the eighteenth century; see Reference 29.

Among the important methodological advances in the nineteenth century was, in addition to the parametric survival analysis models mentioned above, the graphical simultaneous handling of calendar time and age in the Lexis diagram [35, cf. 30].

Two very important themes of modern survival analysis may be traced to early twentieth-century actuarial mathematics: multistate modeling in the particular case of disability insurance [41] and nonparametric estimation in continuous time of the survival function in the competing risk problem under delayed entry and right censoring [13].

At this time, survival analysis was not an integrated component of theoretical statistics. A characteristic skepticism about “the value of life-tables in statistical research” was voiced by Greenwood [20] in the Journal of the Royal Statistical Society, and Westergaard’s [50] guest appearance in Biometrika on “Modern problems in vital statistics” had no reference to sampling variability, this despite the fact that these two authors were actually statistical pioneers in survival analysis: Westergaard [48] by deriving what we would call the standard error of the standardized mortality ratio (rederived by Yule [52]); see [29]) and Greenwood [21] with his famous expression for “the ‘errors of sampling’ of the survivorship tables” (see below).

50.2.2 The “Actuarial” Life Table and the Kaplan–Meier Estimator

In the mid-twentieth century, these well-established demographic and actuarial techniques were presented to the medical-statistical community in influential surveys such as those by Berkson and Gage [4] and Cutler and Ederer [13]. In this approach, time is grouped into discrete units (e.g., 1-year intervals), and the chain of survival frequencies from one interval to the next are multiplied together to form an estimate of the survival probability across several time periods. The difficulty is in the development of the necessary approximations due to the discrete grouping of the intrinsically continuous time and the possibly somewhat oblique observation fields in cohort studies and more complicated demographic situations. The penetrating study by Kaplan and Meier [28], the fascinating genesis of which was chronicled by Breslow [8], in principle eliminated the need for these approximations in the common situation in medical statistics where all survival and censoring times are known precisely. Kaplan and Meier’s tool (which they traced back to Böhmer [7]) was to shrink the observation intervals to include at most one observation per interval. Though overlooked by many later authors, Kaplan and Meier also formalized the age-old handling of delayed entry (actually also covered by Böhmer) through the necessary adjustment for the risk set, the set of individuals alive and under observation at a particular value of the relevant time variable.

Among the variations on the actuarial model, we will mention two.

Harris et al. [23] anticipated much recent work in, for example, AIDS survival studies in their generalization of the usual life table estimator to the situation in which the death and censoring times are known only in large, irregular intervals.

Ederer et al. [14] developed a “relative survival rate … as the ratio of the observed survival rate in a group of patients to the survival rate expected in a group similar to the patients…,” thereby connecting to the long tradition of comparing observed with expected; see, for example, Reference 29).

50.2.3 Parametric Survival Models

Parametric survival models were well-established in actuarial science and demography but have never dominated medical uses of survival analysis. However, in the 1950s and 1960s important contributions to the statistical theory of survival analysis were based on simple parametric models. One example is the maximum likelihood approach by Boag [6] to a cure model assuming eternal life with probability c and lognormally distributed survival times otherwise. The exponential distribution was assumed by Littell [36], when he compared the “actuarial” and the maximum likelihood approach to the “T-year survival rate”, by Armitage [3] in his comparative study of two-sample tests for clinical trials with staggered entry, and by Feigl and Zelen [16] in their model for (uncensored) lifetimes whose expectations were allowed to depend linearly on covariates, generalized to censored data by Zippin and Armitage [53].

Cox [11] revolutionized survival analysis by his semiparametric regression model for the hazard, depending arbitrarily (“nonparametrically”) on time and parametrically on covariates. For details on the genesis of Cox’s paper, see References 42 and 43.

50.2.4 Multistate Models

Traditional actuarial and demographical ways of modeling several life events simultaneously may be formalized within the probabilistic area of finite-state Markov processes in continuous time. An important and influential documentation of this was by Fix and Neyman [18], who studied recovery, relapse, and death (and censoring) in what is now commonly termed an illness-death model allowing for competing risks. Chiang [9], for example, in his 1968 monograph, extensively documented the relevant stochastic models, and Sverdrup [46], in an important paper, gave a systematic statistical study. These models have constant transition intensities, although subdivision of time into intervals allows grouped-time methodology of the actuarial life table type, as carefully documented by Hoem [24].

50.3 Survival Analysis Concepts

The ideal basic independent nonnegative random variables X_i, i = 1, …, n are not always observed directly. For some individuals i, the available piece of information is a right-censoring time U_i, that is, a period elapsed in which the event of interest has not occurred (e.g., a patient has survived until U_i). Thus, a generic survival data sample includes where _i is the smaller of X_i and U_i and D_i is the indicator, I(X_i ≤ U_i), of not being censored.

Mathematically, the distribution of X_i may be described by the survival function

(2)

If the hazard function

(3)

exists, then

(4)

where

(5)

is the integrated hazard over [0, t). If, more generally, the distribution of the X_i has discrete components, then S_i(t) is given by the product-integral of the cumulative hazard measure. Owing to the dynamical nature of survival data, a characterization of the distribution via the hazard function is often convenient. [Note that α_i(t)Δt when Δt > 0 is small is approximately the conditional probability of i “dying” just after time t given “survival” intil time t.] Also, α_i(t) is the basic quantity in the counting process approach to survival analysis (see, e.g., Reference 2).

50.4 Nonparametric Estimation and Testing

The simplest situation encountered in survival analysis is the nonparametric estimation of a survival distribution function based on a right-censored sample of observation times , where the true survival times X_i, i = 1, …, n, are assumed to be independent and identically distributed with common survival distribution function S(t), whereas as few assumptions as possible are usually made about the right-censoring times U_i except for the assumption of independent censoring. The concept of independent censoring has the interpretation that the fact that an individual, i, is alive and uncensored at time t, say, should not provide more information on the survival time for that individual than X_i > t, that is, the right-censoring mechanism should not remove individuals from the study who are at a particularly high or a particularly low risk of dying. Under these assumptions, S(t) is estimated by the Kaplan–Meier estimator [28]. This is given by

(6)

where is the number of individuals at risk just before time t. The Kaplan–Meier estimator is a nonparametric maximum likelihood estimator, and, in large samples, is approximately normally distributed with mean S(t) and a variance that may be estimated by Greenwood’s formula:

(7)

From this result, pointwise confidence intervals for S(t) are easily constructed, and, since one can also show weak convergence of the entire Kaplan–Meier curve to a mean zero Gaussian process, simultaneous confidence bands for S(t) on [0, τ] can also be set up.

As an alternative to estimating the survival distribution function S(t), the cumulative hazard function A(t) = −logS(t) may be studied. Thus, A(t) may be estimated by the Nelson–Aalen estimator

(8)

The relation between the estimators and is given by the product-integral from which it follows that their large-sample properties are equivalent. Though the Kaplan–Meier estimator has the advantage that a survival probability is easier to interpret than a cumulative hazard function, the Nelson–Aalen estimator is easier to generalize to multistate situations beyond the survival data context. We shall return to this below. To give a nonparametric estimate of the hazard function α(t) itself requires some smoothing techniques to be applied.

Right censoring is not the only kind of data incompleteness to be dealt with in survival analysis; in particular, left truncation (or delayed entry) where individuals may not all be followed from time 0 but maybe from a later entry time V_i conditionally on having survived until V_i, occurs frequently in, for example, epidemiological applications. Dealing with left truncation only requires a redefinition of the risk set from the set of individuals still alive and uncensored at time t to the set of individuals with entry time V_i < t and who are still alive and uncensored. With Y(t) still denoting the size of the risk set at time t both Equations (6), (7), and Equation (8) are applicable though one should be aware of the fact that estimates of S(t) and A(t) may be ill-determined for small values of t due to the left truncation.

When the survival time distributions in a number, k, of homogeneous groups have been estimated nonparametrically, it is often of interest to test the hypothesis H₀ of identical hazards in all groups. Thus, on the basis of censored survival data for group h, h = 1, …, k, the Nelson–Aalen estimates have been computed, and based on the combined sample of size n = Σ_hn_h with data , an estimate of the common cumulative hazard function A(t) under H₀ may be obtained by a Nelson–Aalen estimator . As a general statistic for testing H₀, one may then use a k-vector of sums of weighted differences between the increments of and :

(9)

Here, is not among the observed survival times in the hth sample and K_h(t) is 0 whenever Y_h(t) = 0; in fact, all weight functions used in practice have the form K_h(t) = Y_h(t)K(t). With this structure for the weight function, the covariance between Z_h and Z_j given by Equation (9) is estimated by

(10)

and, letting Z be the k-vector (Z₁, …, Z_k′) and Σ the k by k matrix (σ_hj, h, j = 1, …, k), the test statistic X² = Z′Σ⁻Z is asymptotically chi-square distributed under H₀ with k − 1 degrees of freedom if all n_h tend to infinity at the same rate. Here, Σ⁻ is a generalized inverse for Σ. Special choices for K(t) correspond to test statistics with different properties for particular alternatives to H₀. An important such test statistic is the logrank test obtained for K(t) = I(Y(t) > 0). For this test, which has particularly good power for proportional hazards alternatives, Z_h given by Equation (9) reduces to Z_h = O_h − E_h with O_h the total number of observed failures in group h and an “expected” number of failures in group h. For the two-sample case (k = 2), one may of course use the square root of X² as an asymptotically normal test statistic for the null hypothesis. For the case where the k groups are ordered, and where a score x_h (with x₁ ≤ ··· ≤ x_k) is attached to group h, a test for trend is given by T² = (x′Z)²/x′Σx with x = (x₁, …, x_k)′ and it is asymptotically chi-squared with 1 df. The above linear rank tests have low power against certain important classes of alternatives such as “crossing hazards.” Just as for uncensored data, this has motivated the development of test statistics of the Kolmogorov—Smirnov and Cramèr–von Mises types, based on maximal deviation or integrated squared deviation between estimated hazards, cumulative hazards, or survival functions.

50.5 Parametric Inference

The nonparametric methods outlined in the Section 50.4 have become the standard approach to the analysis of simple homogeneous survival data without covariate information. However, parametric survival time distributions are sometimes used for inference, and we shall here give a brief review. Assume again that the true survival times X_i, …, X_n are independent and identically distributed with survival distribution function S(t; θ) and hazard function α(t; θ) but that only a right-censored sample , is observed. Under independent censoring, the likelihood function for the parameter θ is

(11)

The function (11) may be analyzed using standard large-sample theory. Thus, standard tests, that is, Wald, score, and likelihood ratio tests are used as inferential tools. Two frequently used parametric survival models are the Weibull distribution with hazard function αρ(αt)^p−1 and the piecewise exponential distribution with α(t, θ) = α_j for t I_j with I_j = [t_j−1, t_j), 0 = t₀ < t_j < ··· < t_m = ∞. Both of these distributions contain the very simplest model, the exponential distribution with a constant hazard function as null cases.

50.6 Comparison with Expected Survival

As a special case of the nonparametric tests discussed above, a one-sample situation may be studied. This may be relevant if one wants to compare the observed survival in the sample with the expected survival based on a standard life table. Thus, assume that a hazard function α^*(t) is given and that the hypothesis H₀ : α = α^* is to be tested. One test statistic for H₀ is the one-sample log-rank test (O − E^*)/(E^*)^1/2, where E^*, the “expected” number of deaths, is given by (with A^* the cumulative hazard corresponding to α^*). In this case, = O/E^*, the standardized mortality ratio, is the maximum likelihood estimate for the parameter θ in the model α(t) = θ_α^*(t). Thus, the standardized mortality ratio arises from a multiplicative model involving the known population hazard α^*(t). Another classical tool for comparing with expected survival, the so-called expected survival function, arises from an additive or excess hazard model.

50.7 The Cox Regression Model

In many applications of survival analysis, the interest focuses on how covariates may affect the outcome; in clinical trials adjustment of treatment effects for effects of other explanatory variables may be crucial if the randomized groups are unbalanced with respect to important prognostic factors, and in epidemiological cohort studies reliable effects of exposure may be obtained only if some adjustment is made for confounding variables. In these situations, a regression model is useful and the most important model for survival data is the Cox [11] proportional hazards regression model. In its simplest form, it states the hazard function for an individual, i, with covariates Z_i = (Z_i1, …, Z_ip)′ to be

(12)

where β = (β₁, …, β_p)′ is a vector of unknown regression coefficients and α₀(t), the baseline hazard, is the hazard function for individuals with all covariates equal to 0. Thus the baseline hazard describes the common shape of the survival time distributions for all individuals, while the relative risk function exp(β′Z_i) gives the level of each individual’s hazard. The interpretation of the parameter β_j for a dichotomous Z_ij 0, 1 is that exp(β_j) is the relative risk for individuals with Z_ij = 1 compared to those with Z_ij = 0, all other covariates being the same for the two individuals. Similar interpretations hold for parameters corresponding to covariates taking more than two values.

The model is semiparametric in the sense that the relative risk part is modeled parametrically while the baseline hazard is left unspecified. This semiparametric nature of the model led to a number of inference problems, which were discussed in the literature in the years following the publication of Cox’s article in 1972. However, these problems were all resolved and estimation proceeds as follows. The regression coefficients β are estimated by maximizing the Cox partial likelihood

(13)

where and the risk set at time is the set of individuals still alive and uncensored at that time. Furthermore, the cumulative baseline hazard A₀(t) is estimated by the Breslow estimator

(14)

which is the Nelson–Aalen estimator one would use if β were known and equal to the maximum partial likelihood estimate . The estimators based on Equations (13) and (14) also have a nonparametric maximum likelihood interpretation. In large samples, is approximately normally distributed with the proper mean and with a covariance, which is estimated by the information matrix based on Equation (13). This means that approximate confidence intervals for the relative risk parameters of interest can be calculated and that the usual large-sample test statistics based on Equation (13) are available. Also, the asymptotic distribution of the Breslow estimator is normal; however, this estimate is most often used as a tool for estimating survival probabilities for individuals with given covariates, Z₀. Such an estimate may be obtained by the product integral of . The joint asymptotic distribution of and the Breslow estimator then yields an approximate normal distribution for in large samples.

A number of useful extensions of this simple Cox model are available. Thus, in some cases, the covariates are time dependent; for example, a covariate might indicate whether or not a given event had occurred by time t, or a time-dependent covariate might consist of repeated recordings of some measurement likely to affect the prognosis. In such cases, the regression coefficients β are estimated replacing exp(β′Z_j) in Equation (13) by .

Also, a simple extension of the Breslow estimator (14) applies in this case. However, the survival function can, in general, no longer be estimated in a simple way because of the extra randomness arising from the covariates, which is not modeled in the Cox model. This has the consequence that the estimates are more difficult to interpret when the model contains time-dependent covariates. To estimate the survival function in such cases, a joint model for the hazard and the time-dependent covariate is needed.

Another extension of Equation (12) is the stratified Cox model where individuals are grouped into a number, k, of strata each of which has a separate baseline hazard. This model has important applications for checking the assumptions of Equation (12). The model assumption of proportional hazards may also be tested in a number of ways, the simplest possibility being to add interaction terms of the form Z_ij f(t) between Z_ij and time where f(t) is some specified function. Also, various forms of residuals as for normal linear models may be used for model checking in Equation (12). In Equation (12), it is finally assumed that a quantitative covariate affects the hazard log-linearly. This assumption may also be checked in several ways, and alternative models with other relative risk functions r(β′Z_i) may be used. Special care is needed when covariates are measured with error.

50.8 Other Regression Models for Survival Data

Although the semiparametric Cox model is the regression model for survival data that is applied most frequently, other regression models, for example, parametric regression models also play important roles in practice. Examples include models with a multiplicative structure, that is, models like Equation (12) but with a parametric specification, α₀(t) = α₀(t;θ), of the baseline hazard, and accelerated failure-time models.

A multiplicative model with important epidemiological applications is the Poisson regression model with a piecewise constant baseline hazard. In large data sets with categorical covariates, this model has the advantage that a sufficiency reduction to the number of failures and the amount of person-time at risk in each cell defined by the covariates and the division of time into intervals is possible. This is in contrast to the Cox regression model (12), where each individual data record is needed to compute (13). The substantial computing time required to maximize (13) in large samples has also led to modifications of this estimation procedure. Thus, in nested case-control studies the risk set R_i in the Cox partial likelihood is replaced by a random sample _i of R_i. In the accelerated failure-time model, the focus is not on the hazard function but on the survival time itself, much like in classical linear models. Thus, this model is given by log X_i = α + β′Z_i + _i, where the error terms are assumed to be independent and identically distributed with expectation 0. Examples include normally distributed (_i, i = 1, …, n) and error terms with a logistic or an extreme value distribution, the latter giving rise to a regression model with Weibull-distributed lifetimes. Finally, we shall mention some nonparametric hazard models. In Aalen’s additive model, α_i(t) = β₀(t) + β(t)′Z_i(t), the regression functions β₀(t), …, β_p(t) are left completely unspecified and estimated nonparametrically much like the Nelson–Aalen estimator discussed above. This model provides an attractive alternative to the other regression models discussed in this section. There also exist more general and flexible models containing both this model and the Cox regression model as special cases.

50.9 Multistate Models

Models for survival data may be considered a special case of a multistate model, namely, a model with a transient state alive (0) and an absorbing state dead (1) and where the hazard rate is the force of transition from state 0 to state 1. Multistate models may conveniently be studied in the mathematical framework of counting processes with a notation that actually simplifies the notation of the previous sections and, furthermore, unifies the description of survival data and that of more general models like the competing risks model and the illness–death model to be discussed below. We first introduce the counting processes relevant for the study of censored survival data (1). Define, for i = 1, …, n, the stochastic processes

(15)

and

(16)

Then, (15) is a counting process counting 1 at time if individual i is observed to die; otherwise N_i(t) = 0 throughout. Process (16) indicates whether i is still at risk just before time t. Models for the survival data are then introduced via the intensity process, λ_i (t) = α_i(t) Y_i(t) for N_i(t), where α_i(t), as before, denotes the hazard function for the distribution of X_i. Letting N = N₁ + ··· + N_n and Y = Y₁ + ··· + Y_n the Nelson–Aalen estimator (8) is given by the stochastic integral

(17)

where J(t) = I(Y(t) > 0). In this simple multistate model, the transition probability P₀0(0, t), that is, the conditional probability of being in state 0 by time t given state 0 at time 0 is simply the survival probability S(t), which, as described above, may be estimated using the Kaplan–Meier estimator, which is the product-integral of Equation (17). In fact, all the models and methods for survival data discussed above, which are based on the hazard function, have immediate generalizations to models based on counting processes. Thus, both the nonparametric tests and the Cox regression model may be applied for counting process (multistate) models.

One important extension of the two-state model for survival data is the competing risks model with one transient alive state 0 and a number, k, of absorbing states corresponding to death from cause h, h = 1, …, k. In this model, the basic parameters are the cause-specific hazard functions α_h(t), h = 1, …, k, and the observations for individual i will consist of , h = 1, …, k, where D_hi = 1 if individual i is observed to die from cause h and D_hi = 0 otherwise. On the basis of these data, k counting processes for each i can be defined by , and letting N_h = N_h1 + ··· + N_hn, the integrated cause-specific hazard A_h(t) is estimated by the Nelson–Aalen estimator replacing N by N_h in Equation (17). A useful synthesis of the cause-specific hazards is provided by the transition probabilities P_0h(0, t) of being dead from cause h by time t. This is frequently called the cumulative incidence function for cause h and is given by

(18)

and hence it may be estimated by Equation (18) by inserting the Kaplan–Meier estimate for S(u) and the Nelson–Aalen estimate for the integrated cause-specific hazard. In fact, this Aalen–Johansen estimator of the matrix of transition probabilities is exactly the product-integral of the cause-specific hazards.

Another important multistate model is the illness–death or disability model with two transient states, say healthy (0) and diseased (1), and one absorbing state dead (2). If transitions both from 0 to 1 and from 1 to 0 are possible, the disease is recurrent; otherwise it is chronic. On the basis of such observed transitions between the three states, it is possible to define counting processes for individual i as N_hji(t) = number of observed h → j transitions in the time interval [0, t] for individual i, and, furthermore, we may let Y_hi(t) = I (i is in state h at time t −). With these definitions, we may set up and analyze models for the transition intensities α_hji(t) from state h to state j including nonparametric comparisons and Cox-type regression models. Furthermore, transition probabilities P_hj(s,t) may be estimated by product-integration of the intensities.

50.10 Other Kinds of Incomplete Observation

A salient feature of survival data is right censoring, which has been referred to throughout the present overview. However, several other kinds of incomplete observation are important in survival analysis.

Often, particularly when the time variable of interest is age, individuals enter study after time 0. This is called delayed entry and may be handled by left truncation (conditioning) or left filtering (“viewing the observations through a filter”). There are also situations in which only events (such as AIDS cases) that occur before a certain time are included (right truncation). The phenomenon of left censoring, though theoretically possible, is more rarely relevant in survival analysis.

When the event times are only known to lie in an interval, one may use the grouped time approach of classical life tables, or (if the intervals are not synchronous) techniques for interval censoring may be relevant. A common framework (coarsening at random) was recently suggested for several of the above types of incomplete observation.

50.11 Multivariate Survival Analysis

For multivariate survival, the innocent-looking problem of generalizing the Kaplan–Meier estimator to several dimensions has proved surprisingly intricate. A major challenge (in two dimensions) is how to efficiently use singly censored observations, where one component is observed and the other is right censored.

For regression analysis of multivariate survival times, two major approaches have been taken. One is to model the marginal distributions and use estimation techniques based on generalized estimating equations, leaving the association structure unspecified. The other is to specify random effects models for survival data based on conditional independence. An interesting combination of these two methods is provided by copula models in which the marginal distributions are combined via a so-called copula function, thereby obtaining an explicit model for the association structure.

For the special case of repeated events, both the marginal approach and the conditional (frailty) approach have been used successfully.

50.12 Concluding Remarks

Survival analysis is a well-established discipline in statistical theory as well as in biostatistics. Most books on biostatistics contain chapters on the topic, and most software packages include procedures for handling the basic survival techniques. Several books have appeared, among them the documentation of actuarial and demographical know-how by Elandt–Johnson and Johnson [15]; the research monograph by Kalbfleisch and Prentice [27], the first edition of which for a decade maintained its position as main reference on the central theory; the comprehensive text by Lawless [34] also covering parametric models: and the concise text by Cox and Oakes [12], two central contributors to the recent theory. The counting process approach is covered by Fleming and Harrington [17] and by Andersen et al. [2]; see also Reference 25. Later, books intended primarily for the biostatistical user have appeared. These include References 10, 31, 32, 38, and 40. Also, books dealing with special topics, like implementation in the S-Plus software [47], multivariate survival data [26], and the linear regression model [45] have appeared.

References

[1] Aalen, O. O. (1978) Nonparametric inference for a family of counting processes, Annals of Statistics 6: 701–726.

[2] Andersen, P. K., Borgan, Ø., Gill, R. D. & Keiding, N. (1993) Statistical Models Based on Counting Processes. Springer, New York.

[3] Armitage, P. (1959) The comparison of survival curves, Journal of the Royal Statistical Society A 122: 279–300.

[4] Berkson, J. & Gage, R. P. (1950) Calculation of survival rates for cancer, Proceedings of the Staff Meetings of the Mayo Clinic 25: 270–286.

[5] Bernoulli, D. (1766) Essai d’une nouvelle analyse de la mortalité causée par la petite vérole, et des avantages de l’inoculation pour la prévenir, Mémoires de Mathémalique et de Physique de l’Académic Royale des Sciences, Paris Année MDCCLX, pp. 1–45 of Mémoires.

[6] Boag, J. W. (1949) Maximum likelihood estimates of the proportion of patients cured by cancer therapy, Journal of the Royal Statistical Society B 11: 15–53.

[7] Böhmer, P. E. (1912) Theorie der unabhängigen Wahrscheinlichkeiten, Rapports. Mémoires et Procés – verbaux du Congrès International d’Acluaires, Amsterdam 2: 327–343.

[8] Breslow, N. E. (1991) Introduction to Kaplan and Meier (1958). Nonparametric estimation from incomplete observations, in Breakthroughs in Statistics II, S. Kotz & N. L. Johnson, eds. Springer, New York, 311–318.

[9] Chiang, C. L. (1968) Introduction to Stochastic Processes in Bio statistics. John Wiley & Sons, New York.

[10] Collett, D. (2003) Modelling Survival Data in Medical Research, 2nd Ed., Chapman & Hall, London.

[11] Cox, D. R. (1972) Regression models and life-tables (with discussion), Journal of the Royal Statistical Society (B) 34: 187–220.

[12] Cox, D. R. & Oakes, D. (1984) Analysis of Survival Data. Chapman & Hall, London.

[13] Cutler, S. J. & Ederer, F. (1958) Maximum utilization of the life table method in analyzing survival, Journal of Chronic Diseases 8: 699–713.

[14] Ederer, F., Axtell, L. M. & Cutler, S. J. (1961) The relative survival rate: A statistical methodology, National Cancer Institute Monographs 6: 101–121.

[15] Elandt-Johnson, R. C. & Johnson, N. L. (1980) Survival Models and Data Analysis. John Wiley & Sons, New York.

[16] Feigl, P. & Zelen, M. (1965) Estimation of exponential survival probabilities with concomitant information, Biometrics 21: 826–838.

[17] Fleming, T. R. & Harrington, D. P. (1991) Counting Processes and Survival Analysis. John Wiley & Sons, New York.

[18] Fix, E. & Neyman, J. (1951) A simple stochastic model of recovery, relapse, death and loss of patients, Human Biology 23: 205–241.

[19] Gompertz, B. (1825) On the nature of the function expressive of the law of human mortality, Philosophical Transactions of the Royal Society of London, Series A 115: 513–580.

[20] Greenwood, M. (1922) Discussion on the value of life-tables in statistical research, Journal of the Royal Statistical Society 85: 537–560.

[21] Greenwood, M. (1926) The natural duration of cancer, in Reports on Public Health and Medical Subjects, Vol. 33. His Majesty’s Stationery Office, London, pp. 1–26.

[22] Hald, A. (1990) A History of Probability and Statistics and Their Applications Before 1750. John Wiley & Sons, New York.

[23] Harris, T. E., Meier, P. & Tukey, J. W. (1950) The timing of the distribution of events between observations, Human Biology 22: 249–270.

[24] Hoem, J. M. (1976) The statistical theory of demographic rates. A review of current developments (with discussion), Scandinavian Journal of Statistics 3: 169–185.

[25] Hosmer, D. W. & Lemeshow, S. (1999) Applied Survival Analysis. Regression Modeling of Time to Event Data. John Wiley & Sons, New York.

[26] Hougaard, P. (2000) Analysis of Multivariate Survival Data. Springer, New York.

[27] Kalbfleisch, J. D. & Prentice, R. L. (2002) The Statistical Analysis of Failure Time Data, 2nd Ed., John Wiley & Sons, New York.

[28] Kaplan, E. L. & Meier, P. (1958) Non-parametric estimation from incomplete observations, Journal of the American Statistical Association 53: 457–481, 562–563.

[29] Keiding, N. (1987) The method of expected number of deaths 1786–1886–1986, International Statistical Review 55: 1–20.

[30] Keiding, N. (1990) Statistical inference in the Lexis diagram, Philosophical Transactions of the Royal Society London A 332: 487–509.

[31] Klein, J. P. & Moeschberger, M. L. (2003) Survival Analysis. Techniques for Censored and Truncated Data, 2nd Ed., Springer, New York.

[32] Kleinbaum, D. G. (1996) Survival Analysis. A Self-Learning Text. Springer, New York.

[33] Lambert, J. H. (1772) Beyträge zum Gebrauche der Mathematik und deren Anwendung, Vol. III, Verlage des Buchlages der Realschule, Berlin.

[34] Lawless, J. F. (2002) Statistical Models and Methods for Lifetime Data, 2nd Ed., John Wiley & Sons, New York.

[35] Lexis, W. (1875) Einleitung in die Theorie der Bevölkerungsslatistik. Trübner, Strassburg.

[36] Littell, A. S. (1952) Estimation of the T-year survival rate from follow-up studies over a limited period of time, Human Biology 24: 87–116.

[37] Makeham, W. M. (1860) On the law of mortality, and the construction of mortality tables, Journal of the Institute of Actuaries 8: 301.

[38] Marubini, E. & Valsecchi, M. G. (1995) Analysing Survival Data from Clinical Trials and Observational Studies. John Wiley & Sons, Chichester, UK.

[39] de Moivre, A. (1725) Annuities upon Lives: or, The Valuation of Annuities uon any Number of Lives; as also, of Reversions. To which is added, An Appendix concerning the Expectations of Life, and Probabilites of Survivorship. Fayram, Motte and Pearson, London.

[40] Parmar, K. B. & Machin, D. (1995) Survival analysis. A Practical Approach. John Wiley & Sons, Chichester, UK.

[41] du Pasquier, L. G. (1913) Mathematische Theorie der Invaliditätsversicherung, Mitteilungen der Vereinigung der Schweizerische Versicherungs-Mathematiker 8: 1–153.

[42] Prentice, R. L. (1991) Introduction to Cox (1972) Regression models and life-tables, in Breakthroughs in Statistics II, S. Kotz & N. L. Johnson eds. Springer, New York, pp. 519–526.

[43] Reid, N. (1994) A conversation with Sir David Cox, Statistical Science 9: 439–455.

[44] Seal, H. L. (1977) Studies in the history of probability and statistics, XXXV. Multiple decrements or competing risks, Biometrika 64: 429–439.

[45] Smith, P. J. (2002) Analyst’s of Failure Time Data. Chapman & Hall/CRC, London.

[46] Sverdrup, E. (1965) Estimates and test procedures in connection with stochastic models for deaths, recoveries and transfers between different states of health, Skandinavisk Aktuarietidskrift 48: 184–211.

[47] Therneau, T. M. & Grambsch. P. M. (2000) Modeling Survival Data: Extending the Cox Model. Springer, New York.

[48] Westergaard, H. (1882) Die Lehre von der Mortalität und Morbilität. Fischer, Jena.

[49] Westergaard, H. (1901) Die Lehre von der Mortalität und Morbilität, 2. Aufl., Fischer, Jena.

[50] Westergaard, H. (1925) Modern problems in vital statistics, Biometrika 17: 355–364.

[51] Westergaard, H. (1932) Contributions to the History of Statistics. King, London.

[52] Yule, G. (1934) On some points relating to vital statistics, more especially statistics of occupational mortality (with discussion), Journal of the Royal Statistical Society 97: 1–84.

[53] Zippin, C. & Armitage, P. (1966) Use of concomitant variables and incomplete survival information with estimation of an exponential survival parameter, Biometrics 22: 655–672.