Mathematical Foundation of Ellipse Recognition

An ellipse with axes parallel to the coordinate axes of a Cartesian coordinate system and with the center lying in the origin has the well-known equation

x² / a² + y² / b² = 1.

However, we need to consider the general case of a shifted and inclined ellipse. We use the general equation of a conic section:

Ax² + Bxy + Cy² + Dx + Ey + F = 0.

Our aim is to find parameters of an ellipse for which the sum of the squared distances of a set of given points from the ellipse is minimal. Thus our objective function is

(13.1)

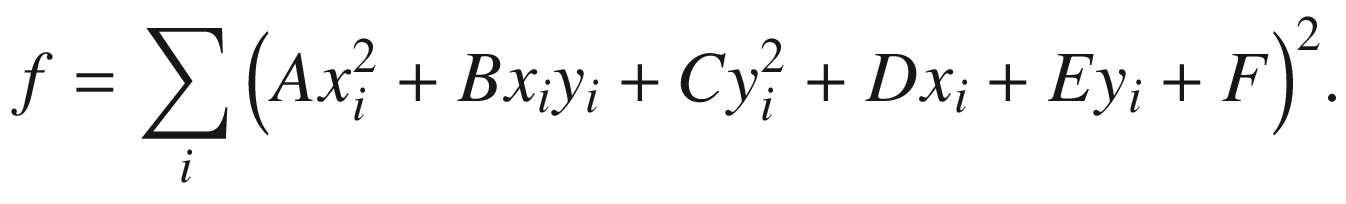
The expression in the parentheses is approximately proportional to the distance of the point (x_i, y_i) from the ellipse. It contains six unknown coefficients A, B, C, D, E, and F. However, it is well known that an ellipse is uniquely defined by five parameters. Therefore we divide all terms of Equation 13.1 by A and denote the new coefficients as follows:

B / A = 2k₁

C / A = k ₂

D / A = 2k₃

E / A = 2k₄

F / A = k ₅

The transformed objective function is

(13.1a)

The partial derivative of f to k₁ is

After multiplying all terms in the parentheses by x_i*y_i we obtain

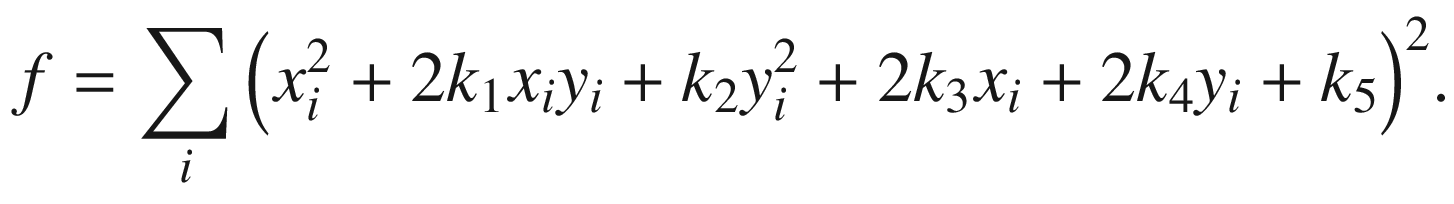
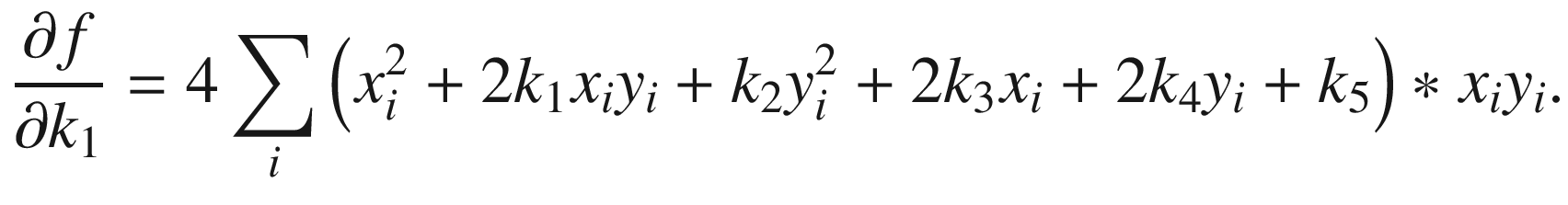
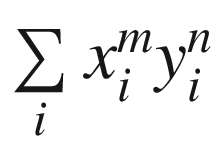We divide it by four and denote each by S(m, n) and obtain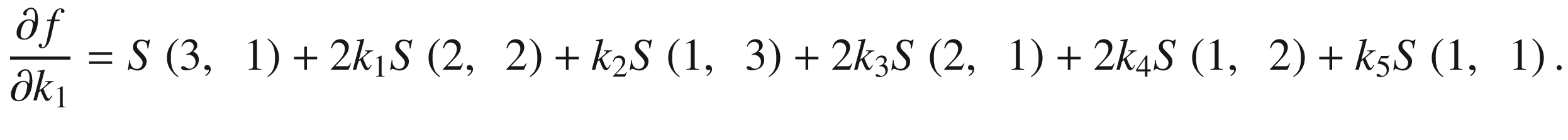

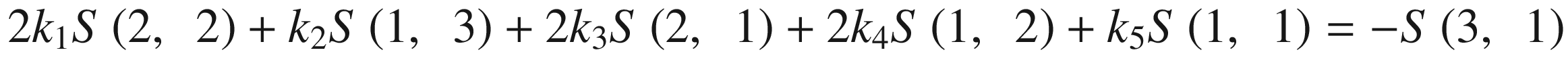
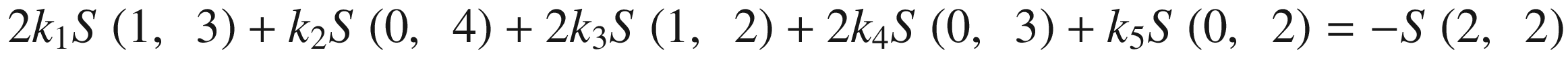
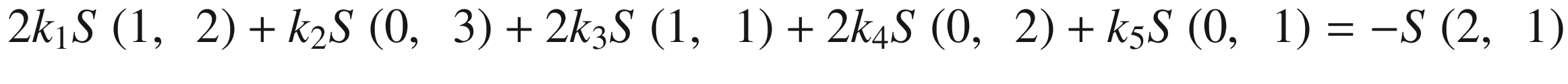
By setting it equal to zero we obtain the first of the five equations for the unknowns k₁, k₂, k₃, k₄, and k₅.

In a similar way we obtain the other four equations:

This system of equations is solved by the well-known Gauss method implemented in the method GetEllipseNew using the method Gauss_K. The sums S(x^m, yⁿ) are calculated by the method MakeSums2 .

The Project WFellipseBike

The form of this project is shown in Figure 13-1.

The user clicks Open image, then selects the folder and the image. The image appears in the left picture box. Then the user clicks Detect edges. There is a numeric up and down tool for the selection of the threshold for edge detection. However, the preselected value of 20 is good for all images and should not be changed. The program runs automatically. It uses the methods described in Chapter 12 for edge detection and polygonal approximation of the edges. Then it uses the method MakeArcsTwo for subdividing the polygons into arcs. This method is slightly different from the MakeArcs3 method described in Chapter 12.

The method FindEllipsesMode is then called to find the ellipses of the wheels of a bike. The method uses arcs sorted according to the number of points. The sorting is performed by the method SortingArcs writing the indexes of the sorted arcs into the array SortArcs . The arc with the greatest number of points stays in SortArcs[0]. Thus the arcs can be taken in the order of decreasing number of points.

The recognition of ellipses is not as simple as that of circles: If the arc transferred to the method GetEllipseNew to find the ellipse containing the arc contains fewer than ten points, sometimes false parameters of the ellipse can be calculated. Therefore we have developed additional means to fix this problem. The method QualityOfEllipseNew calculates the number of points in arcs lying near the ellipse as displayed in Figure 13-2.

The recognition of the wheels is the most important part of the bicycle recognition. When both ellipses of the wheels are recognized, the method RecoFrame is called. It recognizes the direction of travel of the bicycle. This method contains several simple models of different types of the frame. Each type of the frame is presented two times: one with the fork of the front wheel of the bicycle to the left and one with the fork to the right. These models are tested one after the other. Each model is transformed so that the positions of the wheel axles match the centers of the ellipses. A narrow rectangle is formed around each straight segment of the frame. Then all polygons in the processed image are passed through and the lengths of the polygon edges that fit into the rectangles are summed. The model with the greatest sum prevails. In this way the direction of the movement of the bicycle is recognized. 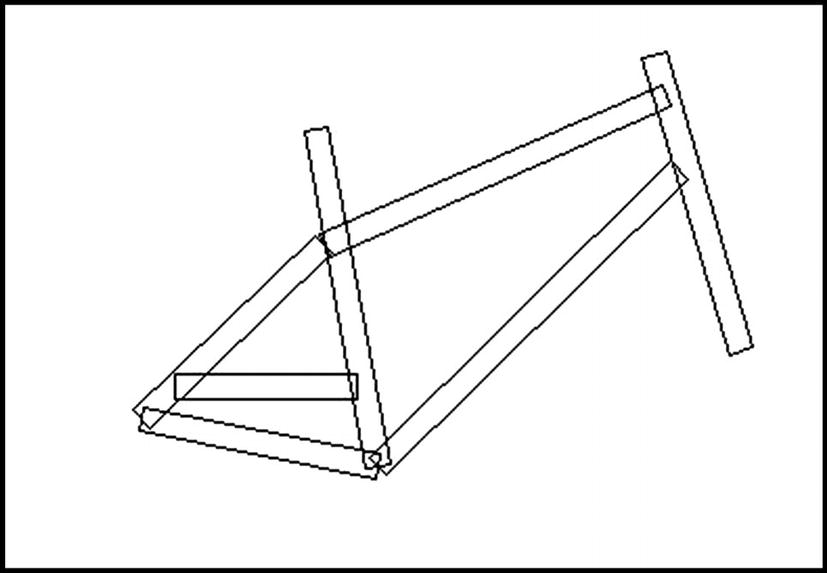An example of the model of the frame is shown in Figure 13-3.

Another Method of Recognizing the Direction

The method just described works when the plane of the frame is at an acute angle to the viewing direction as, for example, in Figure 13-1. In addition, parts of the frame are often obscured by the cyclist’s legs. Therefore we have developed another method DarkSpots which returns the direction of the bike movement: 0 for right and 2 for left. The method makes a box inside of each wheel, calculates histograms of the lightness and sums SumLengths of lengths of almost horizontal polygon edges in these boxes and decides about the drawing direction of the bike. The decision is made by comparing the sum of histogram values below a threshold, i.e. the number of dark pixels in the box, plus 6*SumLenths in both boxes. The greater value indicates the rear wheel and with it also the direction of drawing: if the rear wheel is on the right hand side then the bike moves to left.

When the ellipses of the wheels and the direction of movement are recognized, the ellipses of the wheels and the model of the frame are shown in the right picture box. The message box in the middle of the display shows the message “Bicycle going to left is recognized.” If the user clicks Save result, a text file will be saved on the disk with context corresponding to the following example:

“A bicycle going to left has elliptical wheels.

First: a = 113; b = 173; c = 864; d = 796.

Second: a = 114; b = 173; c = 469; d = 790.”

The notations are as follows: a is the horizontal half-axis of the ellipse, b is its vertical half-axis, c is the x coordinate of the center of the wheel, and d is its y coordinate.

We have tested about 100 photographs showing bicycles on streets in a city. The bicycles were recognized in all photograps except large images of about 2000 × 1500 pixels with small bicycles of about 150 pixels in length (Figure 13-4).

Figure 13-5 provides some examples of images with recognized bicycles.