
Fundamental Materials and Tools 31
peaks (determined by w)orlowerhitprobabilities.However,theirerrorprobabili-
ties get worse as K increases, due to stronger mutual interference. In general,Gold
sequences perform better than the prime codes because the former have code weight
equal to code length and data bit 0s are transmitted with phase-conjugate codes, re-
sulting in a higher SIR.
1.8.3 Combinatorial Analysis for Unipolar Codes
In addition to Gaussian approximation, a more accurate combinatorial method can
be applied to analyze the performance of unipolar codes in OOKmodulation.
As men tio ned in Section 1.8.1, for unipolar codes with the maximum cross-
correlation value of
λ
c
,eachinterferingcodeword(orinterferer)maycontributeup
to
λ
c
hits toward the cross-correlation function. For a given K simultaneous users, the
total number of interferers is given by K −1 =
∑
λ
c
k=0
l
k
,andthetotalnumberofhits
seen by the receiv er in the sampling time is given by
∑
λ
c
k=0
kl
k
,wherel
k
represents
the number of interfering codewords contributing k hits toward the cross-correlation
function. The conditional probability of h aving Z =
∑
λ
c
k=0
kl
k
hits contributed by these
interfering codewords follows a multinomial distribution.Furthermore,inOOK,a
decision error occurs whenever the received data bit is 0, butthetotalnumberofhits
seen by the recei v er in the sampling time is as high as the decision threshold Z
th
.So,
the error probability of unipolar codes with the maximum cross-correlation function
of
λ
c
in OOK is formulated as [21, 27, 30]
P
e
=
1
2
Pr(Z ≥ Z
th
| K simultaneous users, receiver receives bit 0)
=
1
2
∑
∑
λ
c
k=0
kl
k
≥Z
th
(K −1 )!
l
0
!l
1
!···l
λ
c
!
q
l
0
0
q
l
1
1
···q
l
λ
c
λ
c
=
1
2
−
1
2
Z
th
−1
∑
l
1
=0
+(Z
th
−1−l
1
)/2,
∑
l
2
=0
···
+(Z
th
−1−
∑
λ
c
−1
k=1
kl
k
)/
λ
c
,
∑
l
λ
c
=0
(K −1 )!
l
0
!l
1
!···l
λ
c
!
q
l
0
0
q
l
1
1
···q
l
λ
c
λ
c
where the factor 1/2isduetoOOKwithequalprobabilityoftransmittingdatabit
1s and 0s, q
i
denotes the probability of having i ∈ [0,
λ
c
] hits (contributed by each
interfering codeword) toward the cross-correlation function in the sampling time,
∑
λ
c
k=0
l
k
= K −1, and +·, is the floor function. Because q
i
is a probability term, it is
always true that
∑
λ
c
i=0
q
i
= 1.
For example, the error probability of unipolar codes with
λ
c
= 2inOOKisgiven
by
P
e
=
1
2
−
1
2
Z
th
−1
∑
l
1
=0
+(Z
th
−1−l
1
)/2,
∑
l
2
=0
(K −1 )!
l
0
!l
1
!l
2
!
q
l
0
0
q
l
1
1
q
l
2
2
(1.2)
where l
0
+ l
1
+ l
2
= K −1, q
0
+ q
1
+ q
2
= 1, and Z
th
is usually set to w for optimal
decision.
32 Optical Coding Theory with Prime
1.8.4 Hard-Limiting Analysis for Unipolar Codes
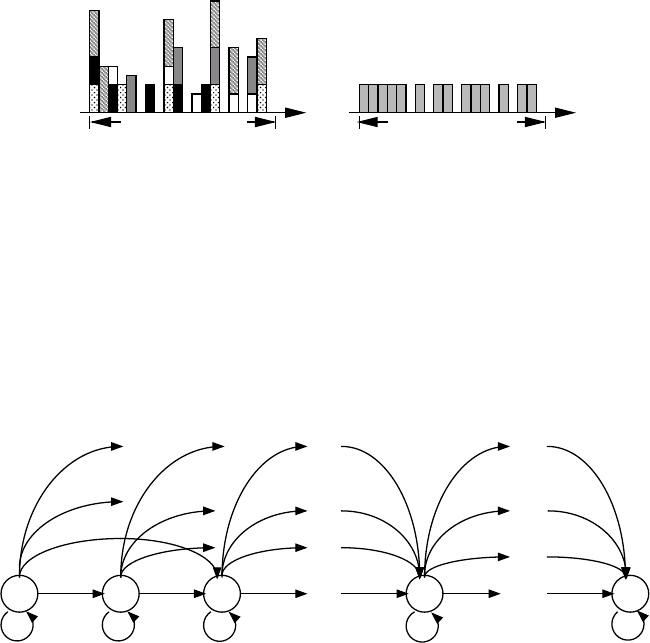
tone code period tone code period
before hard-limiting after hard-limiting
FIGURE 1.4 Hard-limiting of 5 unipolar codewords of weight 5 with unequal pulse height.
It is k nown that a hard-limiter can be placed at the fron t end ofareceiverinorder
to lessen the near-far problem and the localization of stronginterferenceinthere-
ceived signal [21, 30, 33, 34, 37]. As illustrated in Figure 1.4, multiplexed codewords
can have strong interference at some pulse positions, and pulses from various geo-
graphical locations can have different heights (or intensities) due to different amounts
of propagation loss. The hard-limiter equalizes the pulse intensity and interference
strength and, in turn, improves code performance. While a receiver with a hard-
limiter is called a hard-limiting receiver, a regular receiver, such as those studied in
Sections 1.8.1 through 1.8.3, is usually referred to as a soft-limiting receiver.
0 1 2 w
p
0,1
p
0,0
p
1,1
p
2,2
p
1,2
p
0,2
p
0,w
p
0,3
p
1,w
p
2,w
p
i,w
p
1,3
p
1,4
p
i,i
p
2,3
p
i,i+1
p
w-1,w
p
2,4
p
2,5
p
i,i+2
p
w-2,w
p
0,w
p
w,w
i
...
p
i-1,i
p
i-2,i
p
i-3,i
p
i,i+3
p
w-3,w
...
:
:
:
:
:
:
:
:
p
0,i
:
:
:
:
FIGURE 1.5 State transition diagram of a Markov chain with transition probabilities, p
i, j
,
where state i represents that i pulse positions in the address codeword (of weight w)ofa
hard-limiting receiver are being hit [34].
In a hard-limiting receiver, the mutual interference seen atallnonemptypulse
positions of the received signal are equalized and then each eq ualized pulse will
contribute equally toward the cross-correlation fu n ction.Assumethatunipolarcodes
with weight w and the maximum cross-correlation fun ction of
λ
c
are in use. Let
i = {0,1,...,w} represent the states in the Markov chain of Figure 1.5 such that i of
the w pulse positions of the address codeword of the hard-limitingreceiverarehitby
interfering codewords. So, the transition probability p
i, j
of transferring from state i

Fundamental Materials and Tools 33
to state j in the Markov chain is given by [34, 37]
p
i, j
=
∑
λ
c
l=k
(
i
l−k
)(
w−i
k
)
(
w
l
)
q
l
if j = i + k
0otherwise
where k ∈ [0,
λ
c
], q
l
denotes the hit probability of having l ∈ [0,
λ
c
] hits (contributed
by each interfering codeword) toward the cross-correlationfunctioninthesampling
time, and the binomial coefficient is defined as
B
x
y
C
=
x!
y!(x −y)!
for integers x ≥y ≥0, and
-
x
y
.
= 0ifx < y.Becausep
i, j
= 0foralli > j,thetransition
probabilities can be collected into an upper triangular matrix as
P =
p
0,0
p
0,1
··· p
0,w
0 p
1,1
··· p
1,w
.
.
.
.
.
.
.
.
.
.
.
.
00··· p
w,w
and the main-d iagonal elements, p
i,i
for i ∈[0,w],aretheeigenvaluesofP.Withthese
w + 1eigenvalues,P is diagonalizable and P = ABA
−1
for some (w + 1) ×(w + 1)
matrices B, A,andA
−1
,accordingtoTheorem1.6,whereA
−1
is the inverse of A.
So, B is a diagonal matrix with its main-diagonal elements equal totheeigenval-
ues of P.ThecolumnsofA con tain the associated eig envectors of P.Further,from
Section 1.3.4, the (K −1) th power of P can be written as
P
K−1
= AB
K−1
A
−1
where K −1representsthenumberofinterferers(orinterferingcodewords) and
B
K−1
=
p
K−1
0,0
0 ··· 0
0 p
K−1
1,1
··· 0
.
.
.
.
.
.
.
.
.
.
.
.
00··· p
K−1
w,w
Because A is made up of eigenvectors associated with the w + 1eigenvaluesofP, A
and A
−1
are found to be [5, 34, 37]
A =
1
-
w
1
.-
w
2
.
···
-
w
w
.
01
-
w−1
1
.
···
-
w−1
w−1
.
00 1 ···
-
w−2
w−2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 ··· 1
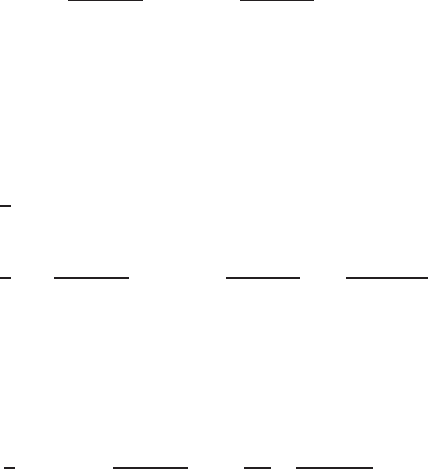
34 Optical Coding Theory with Prime
A
−1
=
1 −
-
w
1
.-
w
2
.
··· (−1)
w
-
w
w
.
01−
-
w−1
1
.
··· (−1)
w−1
-
w−1
w−1
.
00 1 ··· (−1)
w−2
-
w−2
w−2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 ··· 1
Let h
(l)
=(h
(l)
0
,h
(l)
1
,...,h
(l)
i
,...,h
(l)
w
) be a vector collecting all possible interfer-
ence patterns created by l interferers, in which h
(l)
i
represents the probability of hav-
ing i of the w pulse positions in the address codeword of the hard-limitingreceiver
being hit by these l interferers. For K −1interferers,h
(K−1)
can be recursively writ-
ten as [24]
h
(K−1)
= h
(K−2)
P = ··· = h
(0)
P
K−1
=(1, 0,...,0)AB
K−1
A
−1
where “1” represents th e initial condition of having one interferer and “0” represents
the initial condition of having none. After some manipulations, it is found that
h
(K−1)
i
=
w!
i!(w −i)!
i
∑
j=0
(−1)
i−j
i!
j!(i − j)!
p
K−1
j, j
For a hard-limiting receiver, an error occurs when the received data bit is 0 but
the address codeword has the number of pulse positions that are hit by interfering
codewords being as high as the decision threshold Z
th
.So,theerrorprobabilityof
unipolar codes with a maximum cross-correlation function of
λ
c
in a hard-limiting
receiver in OOK is formulated as
P
e,hard
=
1
2
w
∑
i=Z
th
h
(K−1)
i
=
1
2
w
∑
i=Z
th
w!
i!(w −i)!
i
∑
j=0
(−1)
i−j
i!
j!(i − j)!
1
λ
c
∑
k=0
j!(w −k)!
w!( j −k)!
q
k
2
K−1
where the factor 1/2isduetoOOKwithequalprobabilityoftransmittingdatabit1s
and 0s.
For example, the hard-limiting error probability of unipolar codes with
λ
c
= 2in
OOK is given by
P
e,hard
=
1
2
w
∑
i=0
(−1)
w−i
w!
i!(w −i)!
'
q
0
+
iq
1
w
+
i(i −1 )q
2
w(w −1)
(
K−1
(1.3)
where Z
th
is usually set to w for optimal decision.
Figure 1.6 plots the Gaussian-approximated, soft-limiting, and hard-limiting error
probabilities [from Equations (1.1), (1.2), and (1.3), respectively] of the 1-D prime
codes in Section 3.1 ag ainst the number of simultaneous users K.Inthisexample,the
prime codes have
λ
c
= 2, length N = p
2
= {169,289},andweightw = p = {13,17}.

Fundamental Materials and Tools 35
5 10 15 20
10
−14
10
−12
10
−10
10
−8
10
−6
10
−4
10
−2
Error probability P
e
Number of simultaneous users K
Gaussian
Soft limiting
Hard limiting
p = 13
p = 17
p = 13
p = 17
FIGURE 1.6 Gaussian, soft-limiting, and hard-limiting error probabilities of the 1-D prime
codes for p = {13, 17}.
From Section 3.1, the hit probabilities are given by q
0
=(7p
2
− p −2)/ (12p
2
),
q
1
=(2p
2
+ p + 2)/(6p
2
),andq
2
=(p −2)(p + 1)/(12p
2
).ThevarianceinEqua-
tion (1.1) becomes
∑
2
i=1
∑
i−1
j=0
(i − j)
2
q
i
q
j
=(5p
2
−2p −4)/(12p
2
).Ingeneral,the
error prob ab ilities improve as p increases due to heavier code weight w = p and
longer code length N = p
2
.However,theerrorprobabilitiesgetworseasK increases
because of stronger mutual interference. The Gaussian curveisworsethanthesoft-
limiting curve for the same p,butbothcurvesconvergeasK increases. This agrees
with the understanding that Gaussian appro ximation g e nerally gives pessimistic per-
formance, and its accuracy improves with K in accordance with the Central Limit
Theorem. The hard-limiting receiver always results in better perfo r m an ce than the
soft-limiting one because the former lowers the amount of interference. The differ-
ence in error probability enlarges as p increases.
1.8.5 Soft-Limiting Analysis without Chip Synchronization
The combinatorial analyses in Sections 1.8.3 and 1 .8.4 assume that simultaneously
transmitting unipolar codewords are bit asynchronous but chip synchronous, for ease
of mathematical treatment. With the chip-synchronous assumption, the timings of
all transmitting codewor ds ar e per f ectly aligned in time slots (or so-called chips),
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
