
Fundamental Materials and Tools 41
function within the chip interval [r,r ⊕1) can be a triangle, rectangle, or trapezoid,
with an averag e value equal to (I
r
+ I
r⊕1
)/2(e.g.,seeFigure1.7).Denoteq
i, j
as
the (hit) probability of having I
r
= i and I
r⊕1
= j.Theaveragechip-asynchronous
periodic cross-correlation value can be written as the mean (or expected value) such
that
m
asyn
=
λ
c
∑
i=0
λ
c
∑
j=0
,
/
1
0
)
I
r
+
τ
f
(I
r⊕1
−I
r
)
*
d
τ
f
E
q
i, j
=
λ
c
∑
i=0
iq
i,i
+
λ
c
∑
i=0
i−1
∑
j=0
,
/
1
0
)
j +
τ
f
(i − j)
*
q
i, j
d
τ
f
E
+
λ
c
∑
j=0
j−1
∑
i=0
,
/
1
0
)
i +
τ
f
( j −i)
*
q
i, j
d
τ
f
E
The final form in the theorem is derived after some manipulations. The mean is also
equal to w
2
/2N because there always are at most w
2
hits between two correlating
codewords (of weight w and length N)overN chips in OOK.
The chip-asynchronou s variance is derived by taking the expected value of the
second moment of having I
r
= i and I
r⊕1
= j minus the squared mean such that
σ
2
asyn
=
λ
c
∑
i=0
λ
c
∑
j=0
,
/
1
0
)
I
r
+(I
r⊕1
−I
r
)
τ
f
*
2
d
τ
f
E
q
i, j
−
B
w
2
2N
C
2
=
λ
c
∑
i=0
i
2
q
i,i
+
λ
c
∑
i=0
i−1
∑
j=0
,
/
1
0
)
j +
τ
f
(i − j)
*
2
q
i, j
d
τ
f
E
+
λ
c
∑
j=0
j−1
∑
i=0
,
/
1
0
)
i +
τ
f
( j −i)
*
2
q
i, j
d
τ
f
E
−
B
w
2
2N
C
2
=
λ
c
∑
i=0
i
2
q
i,i
+
λ
c
∑
i=0
i−1
∑
j=0
,
/
1
0
)
j
2
+ 2 j(i − j)
τ
f
+(i − j)
2
τ
f
2
*
q
i, j
d
τ
f
E
+
λ
c
∑
j=0
j−1
∑
i=0
,
/
1
0
)
i
2
+ 2i( j −i)
τ
f
+(j −i)
2
τ
f
2
*
q
i, j
d
τ
f
E
−
B
w
2
2N
C
2
The final form in the theorem is derived after some manipulations.
For the chip-synchronous mean and variance in Section 1.8.1, m
syn
= w
2
/(2N)
because there are at most w
2
hits between two correlating codewords (of weight w
and length N)overN ch ips in OOK. The chip-synchronous variance is derived as
σ
2
syn
=
λ
c
∑
i=0
i−1
∑
j=0
(i − j)
2
(q
i
+ q
j
)=
λ
c
∑
i=0
i
2
q
i
−
B
w
2
2N
C
2
by applying
∑
λ
c
i=0
q
i
= 1and
∑
λ
c
i=0
iq
i
= w
2
/(2N).

42 Optical Coding Theory with Prime
So, the difference between these two variances becomes
σ
2
syn
−
σ
2
asyn
=
λ
c
∑
i=0
i
2
q
i
−
λ
c
∑
i=0
i
2
q
i,i
−
λ
c
∑
i=0
i−1
∑
j=0
'
(i − j) j +
(i − j)
2
3
+ j
2
(
(q
i, j
+ q
j,i
)
=
λ
c
∑
i=0
i−1
∑
j=0
,
i
2
2
+
j
2
2
−
'
(i − j) j +
(i − j)
2
3
+ j
2
(E
(q
i, j
+ q
j,i
)
by applying q
i
= 0.5
∑
λ
c
j=0
(q
i, j
+ q
j,i
).Thefinalformofthetheoremisderivedafter
some manipulations.
For the special case of
λ
c
= 1, the chip-asynchronous interference variance can
be rearranged as [21]
σ
2
asyn
=
q
1,0
+ q
0,1
3
+ q
1,1
−q
2
1
=
2
3
(q
1
−q
1,1
)+q
1,1
−q
2
1
=
2
3
(q
1,1
−q
2
1
)
≈
2
3
σ
2
syn
when q
1
≈ q
1,1
.Thepropertiesq
i
= 0.5
∑
1
j=0
(q
i, j
+ q
j,i
),
∑
1
k=0
∑
1
j=0
q
j,k
= 1, q
0
+
q
1
= 1, and q
1,0
= q
0,1
= q
1
−q
1,1
are applied in the d er ivation .
1.8.6 Hard-Limiting Analysis without Chip Synchronization
The more realistic chip-asynchronous assumption can also beappliedtothehard-
limiting receiver for more accurate performance analysis.
0 1/2 1 w
p
0,1/2
p
0,0
p
1/2,1/2
p
1,1
p
1/2,1
p
0,1
p
0,w
p
0,3/2
p
1/2,w
p
1,w
p
i,w
p
1/2,3/2
p
1/2,2
p
i,i
p
1,3/2
p
i,i+1/2
p
w-1/2,w
p
1,2
p
1,5/2
p
i,i+1
p
w-1,w
p
0,w
p
w,w
i
...
p
i-1/2,i
p
i-1,i
p
i-3/2,i
p
i,i+3/2
p
w-3/2,w
...
:
:
:
:
:
:
:
:
p
0,i
:
:
:
:
FIGURE 1.9 State transition diagram of the Markov chain with transitionprobabilitiesp
i, j
,
where state i represents i pulse sub-positions in the address code word (of weight w)ofahard-
limiting receiver are being hit [37].
As illustrated in Figu re 1.7, the chip-asynchronous cross-correlation value in a
chip interval is a linear function of time. By taking the average cross-correlation
Fundamental Materials and Tools 43
value within a chip interval, the contribution of an interfering pulse can be assumed
to have a strength of one half of a hit on average. For unipolar codes with a maxi-
mum cross-correlation function of
λ
c
and weight w,thew pulse positions are here
divided into 2w sub-positions and such a one-half-hit may now occur in one of these
2w sub-positions after hard-limiting. Let i = {0,1/2, 1,3/2,...,w −1/2,w} repre-
sent the states in the Markov chain of Figure 1.9 such that i of the w pulse positions
of the address codeword of the hard-limiting receiver are hitbyinterferingcode-
words. Then, the transition probability p
i, j
of transferring from state i to state j in
the Markov chain is given by [37]
p
i, j
=
∑
λ
c
s=k
∑
λ
c
t=k
(
2i
s+t−2k
)(
2w−2i
2k
)
(
2w
s+t
)
q
s,t
if j = i + k
0otherwise
where k = {0,1/2,1,3/ 2,...,
λ
c
−1/2,
λ
c
},andq
s,t
denotes the (chip-asynchronous)
hit probability defined in Section 1.8.5. Because p
i, j
= 0foralli > j,thetransition
probabilities can be collected into an upper triangular matrix as
P =
p
0,0
p
0,1/2
p
0,1
··· p
0,w
0 p
1/2,1/2
p
1/2,1
··· p
1/2,w
00p
1,1
··· p
1,w
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0··· p
w,w
and the main-diagon al elements, p
i,i
for i = {0,1/2, 1,3/2,...,w −1/2, w},arethe
eigenvalues of P.Withthese2w +1eigenvalues,P is diagonalizable and P = ABA
−1
for some (2w + 1) ×(2 w + 1) matrices B, A,andA
−1
,accordingtoTheorem1.6,
where A
−1
is the inverse of A. B is a diagonal matrix with its main-diagonal elements
equal to the eigenvalues of P.ThecolumnsofA contain the associated eigenvectors
of P.
Following the derivation in Section 1.8.4, and given K −1interferers,
B
K−1
=
p
K−1
0,0
00··· 0
0 p
K−1
1/2,1/2
0 ··· 0
00p
K−1
1,1
··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· p
K−1
w,w
A =
1
-
2w
1
.-
2w
2
.
···
-
2w
2w
.
01
-
2w−1
1
.
···
-
2w−1
2w−1
.
00 1 ···
-
2w−2
2w−2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 ··· 1

44 Optical Coding Theory with Prime
A
−1
=
1 −
-
2w
1
.-
2w
2
.
··· (−1)
2w
-
2w
2w
.
01−
-
2w−1
1
.
··· (−1)
2w−1
-
2w−1
2w−1
.
00 1 ··· (−1)
2w−2
-
2w−2
2w−2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
00 0 ··· 1
can be obtained and eventually the probability of having i of the w pulse positions in
the address codeword of the hard-limiting receiver being hitbyK −1interferersis
given by
h
(K−1)
i
=
(2w)!
(2i)!(2w −2i)!
2i
∑
j=0
(−1)
2i−j
(2i)!
j!(2i − j)!
p
K−1
j/2, j/2
for i = {0, 1/2,1, 3/2,...,w −1/2,w}.
For a hard-limiting receiver, an error occurs when the received data bit is 0 but
the address codeword has the number of pulse positions that are hit by interfering
codewords being as high as the decision threshold Z
th
.So,anerroroccursonlywhen
there are as many as Z
th
pulse positions in the address codeword seeing a sum of
one hit after hard-limiting. This sum of one hit comes from thecasewhenbothsub-
positions of a pulse position are hit with one-half-hit at thesametime.Ifthereexistn
such pulse positions, the remaining w−n pulse positions of the address codeword see
either one-half-hit o r no hit. Let r be the number of pulse positions in which only one
sub-position is hit. The total number of combinations that there are n pulse positions
seeing one-hit and r of them seeing one-half-hit is then given by
-
w
n
.
∑
w−n
r=0
-
w−n
r
.
2
r
.
Furthermore, the probability of a total of 2n + r sub-positions being hit by K −1
interferers is given by h
(K−1)
(2n+r )/2
/
-
2w
2n+r
.
.
So, the error probability of unipolar codes with the maximum cross-correlation
function of
λ
c
in a hard-limiting receiver in OOK under the chip-asynchronous as-
sumption is finally formulated as [37]
P
e,asyn,hard
=
1
2
w
∑
n=Z
th
1
B
w
n
C
w−n
∑
r=0
B
w −n
r
C
2
r
2
h
(K−1)
(2n+r )/2
-
2w
2n+r
.
=
1
2
w
∑
n=Z
th
w!
n!(w −n)!
w−n
∑
r=0
(w −n)!
r!(w −n −r)!
2
r
2n+r
∑
j=0
(−1)
2n+r−j
×
(2n + r )!
j!(2n + r − j)!
1
λ
c
∑
s=0
λ
c
∑
t=0
j!(2w −s −t)!
(2w)!( j −s −t)!
q
s,t
2
K−1
where the factor 1/2isduetoOOKwithequalprobabilityoftransmittingdatabit1s
and 0s.
For example, the chip-asynchronous, hard-limiting error probability of unipolar
Fundamental Materials and Tools 45
codes with
λ
c
= 1inOOKisgivenby
P
e,asyn,hard
=
1
2
2w
∑
i=0
(−1)
2w−i
2w!
i!(2w −i)!
1
q
0,0
+
i(q
0,1
+ q
1,0
)
2w
+
i(i −1 )q
1,1
2w(2w −1)
(
K−1
(1.6)
where Z
th
is usually set to w for optimal decision.
5 10 15 20 25 30 35 40 45 50
10
−12
10
−11
10
−10
10
−9
10
−8
10
−7
10
−6
10
−5
10
−4
10
−3
10
−2
Error probability P
e,hard
Number of simultaneous users K
Simulation
Chip synchronous
Chip asynchronous
(w,N ) = (5,25)
(5,25)
(7,49)
(7,49)
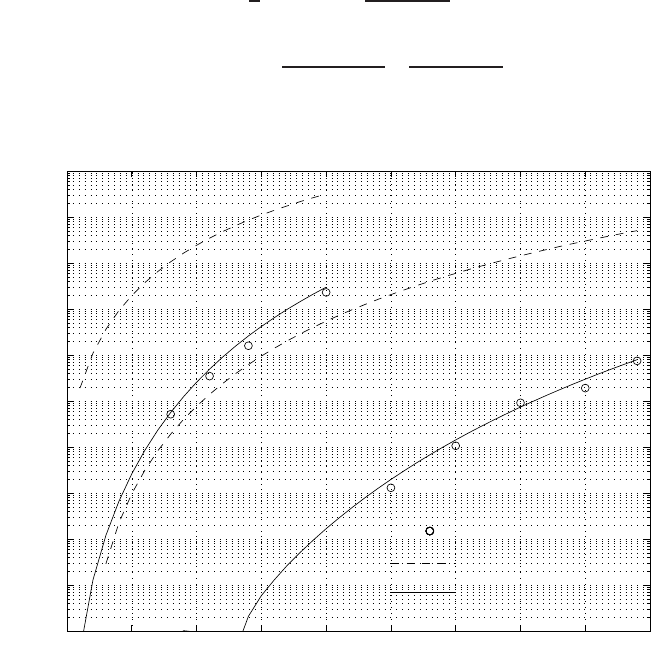
FIGURE 1.10 Hard-limiting error probabilities of the 2-D carrier-hopping prime codes un-
der the chip-synchronous and chip-asynchronous assumptions for length N = {25, 49} and
weight w = {5,7}.
Figure 1.10 plots the hard-limiting error probabilities [fro m P
e,hard
in Equa-
tion (1.3) and P
e,asyn,hard
in Equation (1.6)] of the 2-D carrier-hopping prime codes in
Section 5.1 against the number of simulations users K under the chip-synchronous
and chip-asynch r o nous assumptions, respectively. In this example, the carrier-
hopping prime codes have
λ
c
= 1, L = {5,7}wavelengths, length N = w
2
= {25, 49},
and weight w = {5,7}.WhileEquation(1.3)wasoriginallyderivedfor
λ
c
= 2
codes, it can be applied to the
λ
c
= 1carrier-hoppingprimecodesbysimplyset-
ting q
2
= 0. From Section 5.1, the hit probabilities are given by q
1
= w
2
/(2LN),
q
1,1
= w(w −1)/[2N(N −1 )], q
1,0
= q
0,1
= q
1
−q
1,1
,andq
0,0
= 1 −q
1
−q
0,1
.In
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
