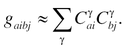Incrementally accelerating the RI-MP2 correlated method of electronic structure theory using OpenACC compiler directives
Janus Juul Eriksen a qLEAP Center for Theoretical Chemistry, Department of Chemistry, Aarhus University, Aarhus C, Denmark
Abstract
In the course of the present chapter, it will be demonstrated how OpenACC compiler directives may be used to compactly and efficiently accelerate the rate-determining step of one of the most routinely applied many-body methods of electronic structure theory, namely the second-order Møller-Plesset (MP2) model in its resolution-of-the-identity (RI) approximated form. Through a total of eight steps, the operations involved in the energy evaluation kernel are incrementally ported to the accelerator(s), and the associated data transfers correspondingly optimized to such a degree that the final versions of the code (using either double or single precision arithmetics) are capable of scaling to as large systems as allowed for by the capacity of the host main memory. The performance of each of the individual code versions is assessed through calculations on a test system of five alanine amino acids in an α-helix arrangement using one-electron basis sets of increasing size (ranging from double- to pentuple-ζ quality). For all but the smallest problem size of the present study, the optimized accelerated code (using six K40 GPUs) is capable of reducing the total time-to-solution by at least an order of magnitude over an optimized CPU-only reference implementation.
Keywords
Quantum chemistry; Electronic structure theory; Coupled cluster methods; Many-body methods; RI-MP2; OpenACC; OpenMP; CUBLAS; Fortran; Hybrid CPU/GPU computing; Asynchronous pipelining; Memory pinning
Acknowledgments
This work was supported by the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement No. 291371 and the developments which led to the final production code used resources of the Oak Ridge Leadership Computing Facility (OLCF) at Oak Ridge National Laboratory, TN, USA, which is supported by the Office of Science of the Department of Energy under Contract DE-AC05-00OR22725. The actual production runs were performed on an NVIDIA test cluster, the access to which is gratefully acknowledged. Finally, the author wishes to thank Thomas Kjærgaard of Aarhus University, Tjerk Straatsma and Dmitry Liakh of OLCF, Luiz DeRose, Aaron Vose, and John Levesque of Cray Inc., as well as Mark Berger, Jeff Larkin, Roberto Gomperts, Michael Wolfe, and Brent Leback of the NVIDIA Corporation.
The purpose of this chapter is to demonstrate how electronic structure many-body theories may be incrementally accelerated in an efficient and portable manner by means of OpenACC compiler directives, with an illustrative application to the RI-MP2 method. The efficiency of the implementation (using six K40 GPUs) is illustrated through a series of test calculations, for which the accelerated code is capable of reducing the total time-to-solution by at least an order of magnitude over an optimized CPU-only reference implementation.
At the end of this chapter the reader will have an understanding of:
• The use of accelerator offloading in quantum chemistry
• Asynchronous pipelining of computations and data transfers
• Hybrid CPU/GPU computing using OpenMP compiler directives
• Fortran interoperability with CUBLAS
• Pinning of memory in CUDA Fortran
Introduction
In electronic structure theory, both coupled cluster (CC) (Čížek, 1966, 1969; Paldus, Čížek, & Shavitt, 1972) and many-body perturbation theory (MBPT) (Shavitt & Bartlett, 2009) offer a systematic approach toward the full configuration interaction (FCI) (Helgaker, Jørgensen, & Olsen, 2000) wave function—the exact solution to the time-independent, nonrelativistic electronic Schrödinger equation—within a given one-electron basis set. In both hierarchies of methods, the Hartree-Fock (HF) solution, in which each electron of a molecular system is treated in a mean-field bath of all other electrons, is the reference to which correlated corrections are made by including excited configurations into the wave function. Moving beyond the HF approximation, not only the effects that prevent two electrons with parallel spin from being found at the same point in space are considered (so-called exchange (or Fermi) correlation, which is fully described by HF theory), but also the corresponding Coulombic repulsion between electrons start being described. This implies that upon traversing up through either of the CC or MBPT hierarchies, increasingly more of such (so-called dynamical) correlation is included in the wave function, with a complete description met at the target FCI limit.
In the MBPT series, the lowest-order perturbative correction to the HF energy for the isolated effect of connected double excitations is that of the noniterative second-order Møller-Plesset (MP2) model (Møller & Plesset, 1934). As an improvement, the CC hierarchy offers the iterative CC singles and doubles (CCSD) model (Purvis & Bartlett, 1982), which accounts not only for connected double excitations, but does so to infinite order in the space of all single and double excitations out of the HF reference. However, the additional accuracy of the CCSD model over the MP2 model comes at a price, as not only is the energy now evaluated iteratively, but each iteration cycle is also significantly more expensive than the simple noniterative evaluation of the MP2 energy, scaling as
![]() as opposed to
as opposed to
![]() (where N is a composite measure of the total system size). Thus, whereas both methods have nowadays become standard tools to computational quantum chemists, the current application range of the MP2 model considerably exceeds that of the CCSD model, due to the practical difference in associated computational cost.
(where N is a composite measure of the total system size). Thus, whereas both methods have nowadays become standard tools to computational quantum chemists, the current application range of the MP2 model considerably exceeds that of the CCSD model, due to the practical difference in associated computational cost.
Nevertheless, the time-to-solution for an average MP2 calculation is still substantial when targeting increasingly larger systems, for example, in comparison with cheaper, albeit less rigorous, and less systematic tools such as those of semiempirical nature or those that calculate the energy from a functional of the one-electron density. For this reason, most efficient implementations of the MP2 model invoke what is known as the resolution-of-the-identity (RI) approximation for reducing the computational cost (the prefactor) as well as lowering the memory constraints (Feyereisen, Fitzgerald, & Komornicki, 1993; Vahtras, Almlöf, & Feyereisen, 1993; Weigend & Häser, 1997; Whitten, 1973). Despite being an approximation to the MP2 model, the development of optimized auxiliary basis sets has managed to significantly reduce the inherent RI error, and for most reasonable choices of the intrinsic thresholds of a modern implementation, the error affiliated with the actual approximation will be negligible. However, while the computational cost is notably reduced in an RI-MP2 calculation with respect to its MP2 counterpart, its formal
![]() scaling with the size of the system will often still make it demanding if no fundamental algorithmic changes are made
(Almlöf, 1991; Ayala & Scuseria, 1999; Doser, Lambrecht, Kussmann, & Ochsenfeld, 2009; Doser, Zienau, Clin, Lambrecht, & Ochsenfeld, 2010; Werner, Manby, & Knowles, 2003). One way in which this challenging issue may be addressed is by attempting to accelerate the rate-determining step in the evaluation of the RI-MP2 energy. However, it should be noted how the clear majority of all electronic structure programs being developed today are primarily written and maintained by domain scientists, many of which hold temporary positions working (simultaneously) on various theoretical and/or application-oriented projects. Thus, while said scientists might decide to implement a given accelerated method from scratch (presumably using some low-level approach unrelated to the language in which the actual code base is written), they might not be responsible for extending it with new features and capabilities nor for the routine maintenance required with the emergence of novel future architectures. Add to that the typical requirements of a single code base and, in particular, platform-independence, which most codes are subject to in the sense that any addition of accelerated code must not interfere with the standard compilation process, and one will potentially arrive at more reasons against investing the necessary efforts than reasons in favor of doing so.
scaling with the size of the system will often still make it demanding if no fundamental algorithmic changes are made
(Almlöf, 1991; Ayala & Scuseria, 1999; Doser, Lambrecht, Kussmann, & Ochsenfeld, 2009; Doser, Zienau, Clin, Lambrecht, & Ochsenfeld, 2010; Werner, Manby, & Knowles, 2003). One way in which this challenging issue may be addressed is by attempting to accelerate the rate-determining step in the evaluation of the RI-MP2 energy. However, it should be noted how the clear majority of all electronic structure programs being developed today are primarily written and maintained by domain scientists, many of which hold temporary positions working (simultaneously) on various theoretical and/or application-oriented projects. Thus, while said scientists might decide to implement a given accelerated method from scratch (presumably using some low-level approach unrelated to the language in which the actual code base is written), they might not be responsible for extending it with new features and capabilities nor for the routine maintenance required with the emergence of novel future architectures. Add to that the typical requirements of a single code base and, in particular, platform-independence, which most codes are subject to in the sense that any addition of accelerated code must not interfere with the standard compilation process, and one will potentially arrive at more reasons against investing the necessary efforts than reasons in favor of doing so.
In the present chapter, it will be demonstrated how to incrementally accelerate many-body theories in an efficient and portable manner by means of OpenACC compiler directives, with an illustrative application to the RI-MP2 method. As with OpenMP worksharing directives for Single-Instruction Multiple-Data (SIMD) instructions on multicore Central Processing Units (CPUs), these are treated as mere comments to a nonaccelerating compiler, and the resulting accelerated code will hence be based on the original source, which, in turn, makes the implementation portable, intuitively transparent, and easier to extend and maintain.
The target architecture, onto which we shall offload parts of the computational workload, will in the present study be Graphics Processing Units (GPUs). The evaluation of the RI-MP2 energy has previously been ported to GPUs in the group of Alán Aspuru-Guzik (Olivares-Amaya et al., 2010; Vogt et al., 2008; Watson, Olivares-Amaya, Edgar, & Aspuru-Guzik, 2010), as, for example, reviewed in a recent contribution to a book devoted to the subject of electronic structure calculations on GPUs (Olivares-Amaya, Jinich, Watson, & Aspuru-Guzik, 2016). However, whereas that implementation made use of the GPU-specific and low-level CUDA compute platform in addition to optimized GPU libraries, the present implementation(s) will not be limited to execution on GPUs; for instance, the current OpenACC standard (version 2.5) offers support for multicore CPUs as well as many-core processors, such as, for example, the Intel Xeon Phi products, but whereas some compiler vendors (e.g., PGI) have started to experiment with OpenACC as an alternative to OpenMP for multicore (host) architectures, no optimizations for many-core x86 processors have been released by any vendor as of yet (mid-2016). Such optimizations are, however, scheduled for future releases. Thus, OpenACC has the potential to offer a single programming model that may encompass host node SIMD execution as well as offloading of compute-intensive code regions to a variety of accelerators, which might make for cleaner, more transparent, and considerably more portable code, also with respect to performance. The present author will leave it to the reader to judge whether or not this is indeed the case for the RI-MP2 case study presented here.
Theory
In the closed-shell (canonical) MP2 model (Møller & Plesset, 1934), the correlation energy is given by the following expression
in terms of two-electron electron repulsion integrals (ERIs), g aibj (Mulliken notation), over spatial (spin-free) HF virtual orbitals a, b and occupied orbitals i, j
as well as the difference in energy between these,
![]() . Besides the final evaluation of the MP2 energy in Eq. (1), the dominant part of an MP2 calculation is the construction of the four-index ERIs. In the so-called resolution-of-the-identity MP2 (RI-MP2) method (Feyereisen et al., 1993; Vahtras et al., 1993; Weigend & Häser, 1997), these are approximated by products of two-, V
αγ
, and three-index, W
aiα
, integrals by using the following symmetric decomposition
. Besides the final evaluation of the MP2 energy in Eq. (1), the dominant part of an MP2 calculation is the construction of the four-index ERIs. In the so-called resolution-of-the-identity MP2 (RI-MP2) method (Feyereisen et al., 1993; Vahtras et al., 1993; Weigend & Häser, 1997), these are approximated by products of two-, V
αγ
, and three-index, W
aiα
, integrals by using the following symmetric decomposition
In Eq. (3), Greek indices denote atomic orbitals within an auxiliary fitting basis set used for spanning the RI, and the fitting coefficients,
![]() , are defined as
, are defined as
In terms of computational cost, the evaluation of two- and three-index integrals and/or the calculation of the fitting coefficients will dominate the overall calculation for small systems (
![]() - and
- and
![]() -scaling processes, respectively). However, upon an increase in system size, the final
-scaling processes, respectively). However, upon an increase in system size, the final
![]() -scaling assembly of the two-electron integrals in Eq. (3) will start to dominate, and this process is thus the ideal candidate for accelerating the RI-MP2 model. If the permutational symmetry of the two-electron integrals in Eq. (3) is taken into consideration, the evaluation of Eqs. (1) and (3) may be collectively expressed as in the pseudocode Fig. 1. Here, nocc, nvirt, and naux denote the number of occupied orbitals, virtual orbitals, and auxiliary basis functions, respectively, while EpsOcc, EpsVirt, and eps denote the corresponding occupied and virtual orbital energies as well as the difference between these. How large the involved dimensions grow for a given calculation depends very much on the size of the actual system as well as the quality of the one-electron basis set used, but for now it suffices to note that typically nocc << nvirt << naux, see also the “Computational Details” section. Finally, the prefactor pre handles the permutational symmetry of the integrals, that is, it is equal to 1.0d0 for coinciding occupied and virtual indices, 2.0d0 when either of these coincide, and a default value of 4.0d0 (Fig. 1).
-scaling assembly of the two-electron integrals in Eq. (3) will start to dominate, and this process is thus the ideal candidate for accelerating the RI-MP2 model. If the permutational symmetry of the two-electron integrals in Eq. (3) is taken into consideration, the evaluation of Eqs. (1) and (3) may be collectively expressed as in the pseudocode Fig. 1. Here, nocc, nvirt, and naux denote the number of occupied orbitals, virtual orbitals, and auxiliary basis functions, respectively, while EpsOcc, EpsVirt, and eps denote the corresponding occupied and virtual orbital energies as well as the difference between these. How large the involved dimensions grow for a given calculation depends very much on the size of the actual system as well as the quality of the one-electron basis set used, but for now it suffices to note that typically nocc << nvirt << naux, see also the “Computational Details” section. Finally, the prefactor pre handles the permutational symmetry of the integrals, that is, it is equal to 1.0d0 for coinciding occupied and virtual indices, 2.0d0 when either of these coincide, and a default value of 4.0d0 (Fig. 1).

Implementation
In all versions of the code (GPU-1 through GPU-8; see the “GPU-1” and “GPU-8” sections), the orbital energies (EpsOcc and EpsVirt) as well as the tensor containing the fitting coefficients (Calpha) are initialized with unique, yet arbitrary single and/or double precision numbers (depending on the context), as the calculation of these are not the objective of the present study. The different codes may be found in full online (Gitlab, 2016), and a short summary of the incremental optimizations occurring in each of the different code versions is provided in Table 1.
Table 1
Summary of the Accelerated RI-MP2 Implementations in the “GPU-1” through “GPU-8” Sections
| Code Version | Summary |
| GPU-1 | Offload the matrix multiplication (dgemm) |
| GPU-2 | Perform the energy summation on the device |
| GPU-3 | Use multiple devices |
| GPU-4 | Hybrid CPU/GPU implementation |
| GPU-5 | Tiling of the Calpha tensor |
| GPU-6 | Asynchronous pipelining |
| GPU-7 | Pinning of Calpha into page-locked memory |
| GPU-8 | Use single-precision arithmetics (sgemm) |
GPU-1
In the first optimization of the kernel, the matrix multiplications (MMs) are offloaded to the GPU, as these BLAS3 library operations are among those that are capable of exploiting the power of the accelerator most optimally (Leang, Rendell, & Gordon, 2014). Here, the compute (CUBLAS) stream is set equal to the default acc_async_sync intrinsic handle (with PGI, by linking with ‘-Mcuda’), and the logical gpu (.true. if a device is present) determines whether to call the CUBLAS or CPU-optimized (e.g., MKL) dgemm routine through the interface. Thus, in a CPU-only run, both the MM and the subsequent energy summation are performed on the host, whereas in the present GPU-1 scheme, the former of these is performed on the device and the latter on the host (Fig. 2).

GPU-2
In the first optimization of the GPU code, the copyout (host update) of the g_ij intermediate is avoided by performing the worksharing energy summation on the device instead. By avoiding the (redundant) data transfer of g_ij, the entire kernel has effectively been ported to the device. As such, the implementation will take full advantage of the accelerator, but we note how the host is now completely idle during the computation, an issue which we shall attend to later in the “GPU-4” section. For now, we note that both the EpsOcc and EpsVirt vectors have been declared as present in the OpenACC parallel region in order to avoid excessive data movement, so these have to join the Calpha tensor in the copyin clause of the outer data region directive. The two relevant tensor elements of the EpsOcc vector have furthermore been explicitly fetched into the highest level of the cache, even though most, if not all, compilers would do this automatically. However, verbosity is used here not only for pedagogical purposes; rather, it is used to aid the compiler in the analysis of the nested loop, in the same way as the independent clause has been added (loop iterations are explicitly data-independent) and the GPU parallelization of the energy summation has been explicitly mapped to thread gangs (thread blocks) and vectors (individual threads), although the compiler might decide upon this partitioning even in the absence of the clauses. In general, while an initial OpenACC port can, and perhaps should be overly implicit, it is good practice to enforce the final implementation to be verbose, not only to make it more transparent to the present and future developers of the code, but also to guarantee comparable execution with compilers from different vendors. However, we have here abstained from explicitly mapping the loops to x number of thread blocks (num_gangs( x )) of length y (vector_length( y )), as this would make the code less general in case it should also be able to target other types of architectures, cf. the “Introduction” section (Fig. 3).

GPU-3
Having succeeded in porting the kernel to a single device, as opposed to a host-only execution, the next obvious step is to port it to multiple devices. In doing so, one has the option between (at least) two different strategies, namely: using (1) message passing (MPI); or (2) worksharing compiler directives (OpenMP). For option (1), each MPI rank has to create its own context, and sharing the host main memory among the individual ranks is thus nontrivial (although indeed possible). Furthermore, one would have to create an additional layer of communication on top of a possible existing MPI intra-node parallelization of the kernel. For option (2), on the other hand, the individual devices are mapped to individual OpenMP threads, which among them share a common shared memory context. For memory-intensive many-body methods in electronic structure theory, this is an attractive feature as the individual tensors often grow very large in size. Thus, by embedding the OpenACC implementation of the “GPU-2” section within an OpenMP parallel region, we can extend the accelerated code from one to multiple devices (Fig. 4).

Here, a total of acc_num_devices threads is spanned in the parallel region (queried from the acc_get_num_devices(acc_device_type) API function) and each individual host thread (gpu_id) gets assigned its own device through a call to the acc_set_device_num() API routine. The individual CUBLAS handles are stored in a vector (cublas_handle) of length n_threads. Finally, we note how the loop scheduling has been explicitly declared in the worksharing over the outermost j-loop, as this is heavily load-imbalanced; however, the additional overhead introduced by the dynamic scheduling is negligible compared to the idle time which would be introduced with the default static schedule.
GPU-4
In the GPU-3 version of the code in the “GPU-3” section, only the devices attached to the compute node take part in the workload, while the node stays idle throughout the evaluation of the RI-MP2 energy. In order to alleviate this waste of resources, one might consider increasing the number of OpenMP threads in the parallel region from acc_num_devices to, for example, the number of CPU cores or, more generally, the OMP_NUM_THREADS environment variable. However, by doing so, the load imbalance of the j-loop would be exposed due to the heterogeneity in architecture. Thus, instead one needs to flatten (or collapse) the two outer loops into one large, composite outer loop with loop cycles of identical size. This way, the host cores might be regarded as accelerators on their own, although some that are operating at a significantly lower processing power than the device(s) (Fig. 5).

In the present version of the code, the default value of the gpu logical (prior to the parallel region) is .false., and the loop scheduling is now decided upon at runtime; more specifically, a static schedule (with default chunk size) is chosen if accelerators are absent (the computational resources amount to the OMP_NUM_THREADS host cores), while in the heterogeneous case of hybrid host/device execution ([OMP_NUM_THREADS − acc_num_devices] host cores and acc_num_devices devices), the same dynamic schedule (with a chunk size of 1) as for the GPU-3 code is chosen. It should be noted—as is often the case when optimizing the code for accelerator offloading—that the present CPU-only version of the code even marks an improvement over the original code in the “GPU-1” section, in particular for small, although less so for large matrix dimensions, as running n_threads single-threaded MMs concurrently will generally be more efficient than running a single multithreaded MM (over n_thread threads) sequentially n_thread times. However, this performance improvement occurs at the expense of having to store multiple private copies of the g_ij tensor (of size nvirt**2), but in the grander scheme of things, for example, considering that the Calpha tensor is of size naux*nvirt*nocc, cf. the “Computational Details” section, this is next to negligible.
GPU-5
As mentioned at the end of the “GPU-4” section, the involved tensors—in particular that containing the fitting coefficients, Calpha—grow large upon moving to larger system sizes and/or larger basis sets (collectively referred to herein as a transition to increasingly larger problem sizes). For instance, even for moderate-sized problems (cf. the “Results” section), the memory constraints may be in excess of what is feasible on a Kepler K20X card (6 GB), and for increasingly larger problem sizes, the total device memory requirements can grow well beyond what is possible on a Kepler K40 card (12 GB). However, since the entire premise for the RI-MP2 model is that it should be able to target larger problem sizes than the regular MP2 model (which, of course, is the regime where acceleration of the kernel is most needed), these constraints, in combination with the fact that only two tiles of the fitting coefficient tensor are required to be residing on the device in each loop cycle (i.e., Calpha(:,:,j) and Calpha(:,:,i)), give motivation to a tiled implementation (Fig. 6).

Obviously, the increased data movement (the (potential) copyin of the i-th and j-th tile in each loop cycle) in the present version of the code over the single, but considerably larger data transfer in the previous implementations introduces a net slow-down. However, by separating the kernel into individual data transfers, we shall now see how this enables a pipelining of operations, while lowering the memory requirements dramatically, cf. the “Results” section.
GPU-6
In the GPU-5 version of the code, the requirements on the size of the device main memory were markedly reduced, but since the data movement and computations became synchronized at the same time, as these occur on the same stream (that corresponding to the default acc_async_sync handle), the implementation is significantly slower than the GPU-4 version in the “GPU-4” section. If, however, the available device main memory offers the storage of more than two tiles of size naux*nvirt, the copyin of the tile(s) required for the next loop cycle may be scheduled to occur concurrently with the current computations without the need for any immediate synchronization. This sort of pipelining can be achieved by making only a few small modifications to the GPU-5 version of the code (Fig. 7).

In this asynchronous version of the code, the data transfers are done on the streams corresponding to handles 0 and 1 (i.e., the possible values of mod(inc,2)), while the computations—that is, the MMs and the energy summation—are carried out on the stream mapped to handle 2. Note how the loop index, which might usually be used for pipelining, is not a valid choice in the present context due to the dynamic OpenMP scheduling. Instead, a thread-private incremental counter (inc) is introduced. Furthermore, the CUBLAS stream is now not the default one (acc_async_sync), but rather explicitly mapped to async handle 2, and the data dependencies are controlled through the use of (async) wait directives. In particular, two streams are used for data transfers such that the waits within the ji-loop are made asynchronous as well. However, despite pipelining the data transfers and computations, the former of these two operations will still dominate whenever the (potential) copyins of the two tiles of Calpha take longer than the CUBLAS dgemm. As we shall see in the “Results” section, this is indeed the case; hence, whereas the present code is a clear improvement over the synchronous GPU-5 version, it is still significantly slower than the native, memory-intensive GPU-4 version. To understand why, and to see how to remedy this, we shall need to revisit how (a)synchronous device data transfers are done with CUDA/OpenACC.
GPU-7
Whenever memory is allocated on the host through, for example, an allocate statement, it is stored in so-called nonlocked pages such that the memory might potentially be swapped out to disk if need be. However, GPU devices cannot access data directly from nonlocked (or pageable) host main memory, so at the time when the data transfer is invoked, the driver needs to access every single page of the nonlocked memory, copy it into a page-locked (or pinned) memory buffer (which needs to be allocated beforehand), followed next by the actual transfer, the wait for completion, and finally the deletion of said page-locked buffer. Although the size of these buffers can be altered (in the PGI OpenACC runtime, for instance, this is done through the PGI_ACC_BUFFERSIZE environment variable), it is not intuitive what buffer size will be most suitable for a given problem size (Fig. 8).

Now, instead of using pinned memory as merely a staging area for transfers between the device and the host, one might instead choose to directly allocate host variables in pinned memory. Traditionally, this is done by allocating/deallocating host main memory with the cudaHostAlloc / cudaFreeHost routines of the CUDA API and subsequently pinning/unpinning the allocation by calling cudaHostRegister / cudaHostUnregister. In the PGI-specific CUDA Fortran extension, however, the use of pinned memory may be enforced simply by applying the pinned variable attribute on the declaration of an allocatable tensor. Besides the allocation of Calpha in pinned rather than pageable memory, no further changes are made with respect to the GPU-6 version of the code in the “GPU-6” section. However, since some operating systems and installations may restrict the use, availability, or size of page-locked memory, the allocation has been augmented by a third argument, which, if it fails (pinned_stat is .false.) makes the user aware that the allocation has defaulted to a regular allocation in paged memory.
As we shall see in the “Results” section, this simple change to the declaration of the Calpha tensor now makes the calculations for all relevant problem sizes completely compute-bound in the same way as the native GPU-4 version of code. Thus, as the present version of the code uses vastly less device memory than the GPU-4 version, it will in principle scale to as large dimensions of Calpha as may fit into host main memory. Furthermore, as the initial copyin of the entire Calpha is avoided, the present version of the code will actually scale better than the GPU-4 version for all but the smallest problem sizes, cf. the “Scaling With Number of Devices” section.
GPU-8
In standard RI-MP2 implementations, all involved steps (evaluation of ERIs, construction of fitting coefficients, and the final energy assembly) are performed using double precision arithmetics. However, motivated by two recent papers (Knizia, Li, Simon, & Werner, 2011; Vysotskiy & Cederbaum, 2011), which both claim that single precision arithmetics can be applied for the construction of the four-index ERIs in Eq. (3) (since this step is being performed in an orthogonal basis), we shall now, as a final optimization step, do exactly this by substituting the dgemm by a corresponding sgemm in the code. Here, the interface to sgemm is formulated in precisely the same way as the interface to dgemm. Not only is the performance bound to improve from the use of single precision arithmetics, but also the storage requirements on the tiles of the Calpha tensor and the g_ij intermediate are further lowered by a factor of two (Fig. 9).

Results
In the present section, we shall numerically compare the different versions of the RI-MP2 kernel discussed in the “Implementation” section. Following some initial details in the “Computational Details” section on the calculations to follow, we first compare the various codes on an equal footing for execution on a single accelerator device in the “Scaling With Problem Size” section, while in the “Scaling With Number of Devices” section, we shall look at the scaling with the number of available devices. The accumulated performance against CPU-only calculations is reported for the best among the proposed schemes in the “Total Performance” section.
Computational Details
For the purpose of evaluating the various GPU schemes of the “Implementation” section, we shall conduct performance tests on four problems of increasing size, namely the [ala]-5 system (five alanine amino acids in an α-helix arrangement) in the cc-pVXZ (X = D, T, Q, and 5) basis sets (Dunning Jr., 1989) and corresponding cc-pVXZ-RI auxiliary basis sets (Hättig, 2005; Weigend, Köhn, & Hättig, 2002), which are of double-, triple-, quadruple-, and pentuple-ζ quality. Denoting the four problems as DZ, TZ, QZ, and 5Z, respectively, the problem sizes are defined in terms of the number of occupied orbitals, virtual orbitals, auxiliary basis functions, and size of Calpha in GB (mem) as:
• DZ: nocc = 100; nvirt = 399; naux = 1834; mem = 0.6
• TZ: nocc = 100; nvirt = 1058; naux = 2916; mem = 2.5
• QZ: nocc = 100; nvirt = 2140; naux = 4917; mem = 8.4
• 5Z: nocc = 100; nvirt = 3751; naux = 7475; mem = 22.4
In terms of computational hardware, the accelerators used are NVIDIA Kepler K40 GPUs (2880 processor cores @ 745 MHz (GPU Boost @ 875 MHz enabled, cf. the “GPU boost” section) and 12 GB main memory) and the host nodes are Intel Ivy Bridge E5-2690 v2, dual socket 10-core CPUs (20 cores @ 3.00 GHz and 128 GB main memory). The (single- or multi-threaded, depending on the version of the code) host math library is Intel MKL (version 11.2) and the corresponding device math library is CUBLAS (CUDA 7.5). All calculations are serial (non-MPI), and the OpenMP- and OpenACC-compatible Fortran compiler used is that of the PGI compiler suite (version 16.4).
GPU boost
On the K40 GPUs, the base core clock rate is 745 MHz. However, provided that the power and thermal budgets allow for it, e.g., for small problem sizes in the current context, the GPU offers the possibility of boosting the application performance by increasing the GPU core (and memory) clock rates. Since the GPU will dynamically reset the clock rates to the default values whenever it cannot safely run at the selected clocks, the use of GPU Boost is an additional (free) way of enabling even more performance gain from the accelerator. From the results in Fig. 10, we note how for the double- and triple-ζ calculations in double precision (scheme GPU-7), the net increase amounts to 7–13%, while the effect of the increased application clock rates diminishes for the larger QZ problem. For the corresponding calculations in single precision, however, the increase in performance comes close to matching the theoretical increase in moving from 745 MHz over 810 MHz (9%) to 875 MHz (17%), and the results in Fig. 10 hence mirror the intrinsic difference between the performance of single and double precision math library routines as well as the possible gain of using the former of these whenever possible.

Scaling With Problem Size
In Fig. 11, results are presented for the relative speed-up against a CPU-only run for the eight different GPU schemes of the “Implementation” section. Schemes 1–3 are compared against the CPU-only version of scheme 1 (note that schemes 2 and 3 are identical for execution on a single GPU, cf. the “GPU-3” section), whereas schemes 4–7 are compared against the CPU-only version of scheme 4, which, itself, gives speed-ups of 48% (cc-pVDZ), 27% (cc-pVTZ), 14% (cc-pVQZ), and 7% (cc-pV5Z) over scheme 1 for the four different problem sizes. Finally, scheme 8 is compared against a CPU-only single precision version of scheme 4, which gives speed-ups of 89% (cc-pVDZ), 101% (cc-pVTZ), 100% (cc-pVQZ), and 106% (cc-pV5Z) over scheme 4 in double precision. For the largest of the four problem sizes (5Z), only the CPU-only versions of schemes 1 and 4 as well as the OpenACC-accelerated schemes 5–8 were possible to run due to the large memory requirements, cf. the discussion in the “GPU-5” section.

As is clear from Fig. 11, the performance gained from exclusively using the GPU is not as good as that gained from using both the CPU and the GPU simultaneously. Focusing further on the hybrid schemes (4–8), we note how the optimal speed-up for the schemes using double precision arithmetics is met (on a K40 card) for problem sizes somewhere in-between that of the TZ and QZ problems of the present test, while for scheme 8, which uses single precision arithmetics, a small improvement is still observed in moving from the QZ to the 5Z problem. By comparing the tiled schemes 5 and 6 with the full scheme 4, it appears that the performance of the former schemes suffers from the increased amount of data transfers for problems DZ, TZ, and QZ, whereas for the pinned scheme 7, this is only the case for the smallest DZ problem. For the largest of the problem sizes (5Z), the tiled schemes cannot be compared to the full scheme 4, but from profiling runs using nvprof, it is confirmed that the total compute time for schemes 6 and 7 is equal to the time spent in the dgemm and the OpenACC parallel region. For scheme 8, profiling runs too confirm that the calculations are compute-bound, but now also for the smallest DZ problem, as a result of the smaller tiles that need to be copied to the device in each loop cycle.
Scaling With Number of Devices
With the results in the “Scaling With Problem Size” section illustrating how the different schemes perform on a single accelerator device, we now turn to the scaling with the number of devices. In Fig. 12, the scaling with the number of GPUs is presented, reported in terms of the relative deviation from ideal behavior. For scheme 3, the ideal scaling is a simple proportionality with the number of GPUs (performance doubling, tripling, etc., on two, three, etc., GPUs), whereas for schemes 4–8, this is not the case, as each CPU core is now treated as an accelerator on its own, cf. the discussion in the “GPU-4” section. Thus, the ideal speed-up for the homogeneous scheme 3 (R 1) and the heterogeneous schemes 4–8 (R 2) are defined as
In the definition of R 2 in Eq. (5b), the constant factor S = N threads K, where K is the time ratio between a CPU-only calculation (N threads = OMP_NUM_THREADS; N GPUs = 0) and a GPU-only calculation using a single GPU (N threads = N GPUs = 1), accounts for the relative difference in processing power between a single CPU core (assuming ideal OpenMP parallelization on the host) and a single GPU.

From Fig. 12, we note how the scalings of schemes 3 and 4 are practically identical, as are those of schemes 7 and 8; for all of the different schemes, a clear improvement in the scaling is observed in moving to larger problem sizes, but this improvement is somewhat less prominent for the asynchronous tiled scheme 6 and again much less for the synchronous scheme 5. While schemes 3 and 4, which store the full Calpha tensor in device main memory, scale the best for small problem sizes, the picture is shifted in favor of the tiled schemes (in particular the pinned schemes 7 and 8) upon moving to larger problem sizes, since the large copyin of Calpha prior to the actual energy evaluation is avoided in these.
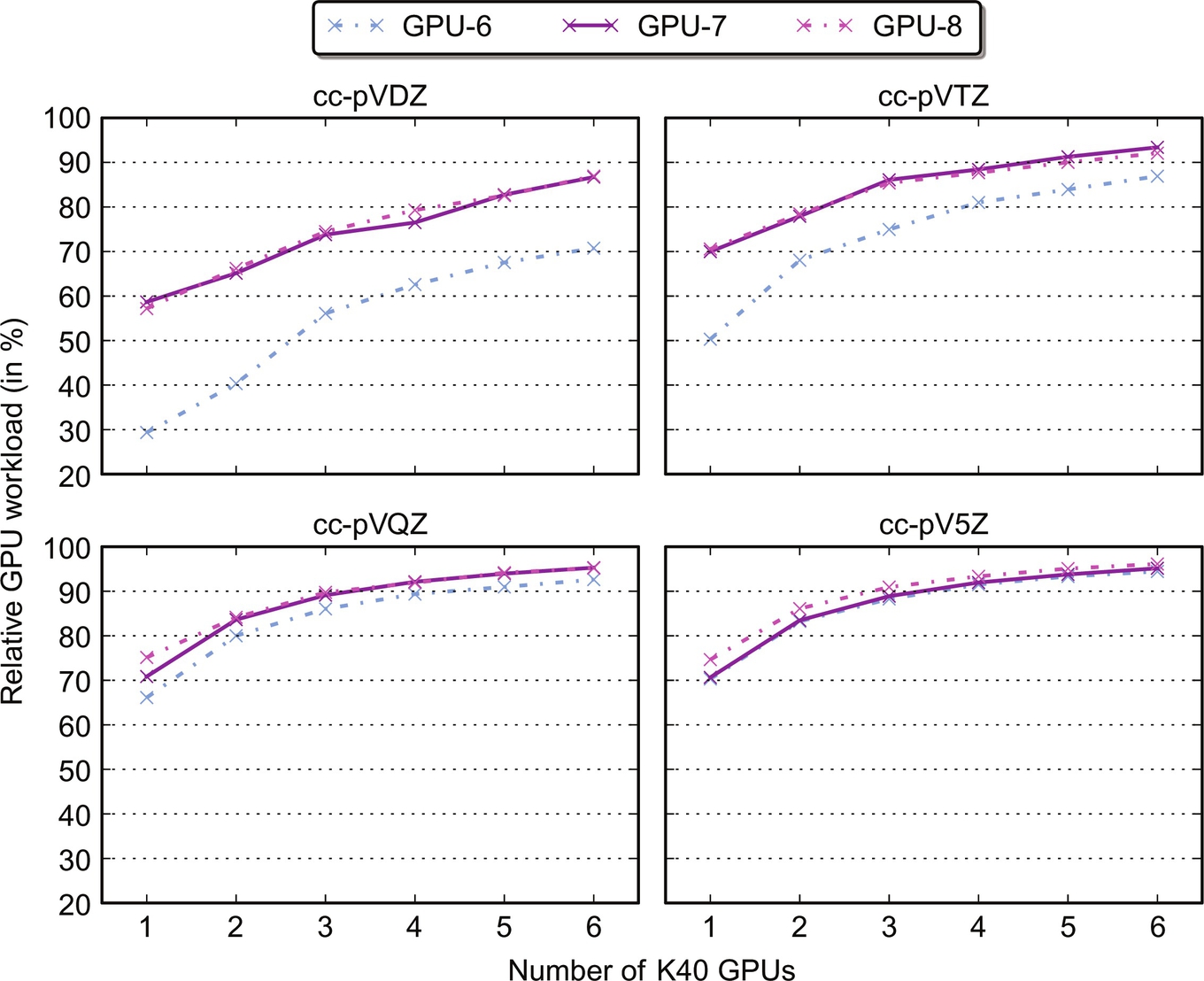
Finally, by noting that for the hybrid schemes 4–8 there is a total of (nocc(1+nocc))/2 tasks that need to be distributed among the CPU cores and accelerator devices, we may complement the scaling results in Fig. 12 by corresponding results for the relative GPU workload. These results are presented in Fig. 13 for schemes 6–8; for all of the four problem sizes, the utilization of the GPUs is better for the pinned schemes 7 and 8—as a result of the faster data transfers—but less so upon moving to increasingly larger problems. Also, we note how for the present problem sizes and CPU/GPU hardware, the actual utilization of the host node is minor (less than 10%) when, say, three or more GPUs are attached to said node. Still, the hybrid schemes, with the exception of the synchronous scheme 5, are always faster than the corresponding GPU-only scheme 3.
Total Performance
Having assessed how each of the proposed schemes accelerate the RI-MP2 energy evaluation for execution on a single GPU, as well as how the schemes that may utilize more than one GPU scale with the available resources, we now combine the results of Figs. 11 and 12 in Fig. 14, which reports the multi-GPU speed-up of schemes 7 and 8 over the double and single precision CPU-only versions of scheme 4. In Fig. 14, the speed-up resulting from using single rather than double precision arithmetics has also been indicated. From the results, it is obvious that both schemes perform well with the number of GPUs, but that scheme 8 generally scales better than scheme 7. In fact, using six K40 GPUs, as in the present study, is seen to reduce the total time-to-solution over the CPU-only versions of either scheme 7 or 8 by more than an order of magnitude for all but the smallest possible problem sizes, as is visible from the total timings plotted in Fig. 15. This is indeed a noteworthy acceleration of the RI-MP2 kernel, since the use of compiler directives—as long as the complete fitting coefficients fit into main memory on the host—makes it somewhat unnecessary to explicitly MPI parallelize the code.


Summary and Conclusion
In the present chapter, OpenACC compiler directives have been used to compactly and efficiently accelerate the
![]() -scaling rate-determining step of the RI-MP2 method. Through a total of eight steps, the computations have been incrementally offloaded to the accelerators (GPUs in the present context), followed by a subsequent optimization of the involved data transfers. In the final versions of the code, computations and data traffic have been asynchronously pipelined, and an explicit pinning of the involved tensors in page-locked host memory has been introduced in order to make the tiled GPU schemes compute-bound on par with the more memory-intensive schemes. Due to their minimal memory footprints and efficient dependence on optimized math libraries, the two final versions of the code using either double or single precision arithmetics are capable of scaling to as large systems as allowed for by the capacity of the host main memory.
-scaling rate-determining step of the RI-MP2 method. Through a total of eight steps, the computations have been incrementally offloaded to the accelerators (GPUs in the present context), followed by a subsequent optimization of the involved data transfers. In the final versions of the code, computations and data traffic have been asynchronously pipelined, and an explicit pinning of the involved tensors in page-locked host memory has been introduced in order to make the tiled GPU schemes compute-bound on par with the more memory-intensive schemes. Due to their minimal memory footprints and efficient dependence on optimized math libraries, the two final versions of the code using either double or single precision arithmetics are capable of scaling to as large systems as allowed for by the capacity of the host main memory.
The evaluation of the RI-MP2 energy has been accelerated using a high-level approach through the use of compiler directives rather than a more low-level, albeit possibly more efficient approach through a recasting of the code using the CUDA compute platform. This has been a deliberate choice, based on a number of reasonings. First and foremost, it is the opinion of the present author that accelerated code needs to be relatively easy and fast to implement, as new bottlenecks are bound to appear as soon as one part of a complex algorithm has been ported to accelerators (cf. Amdahl’s law). Second, the use of compiler directives guarantees—on par with the use of OpenMP worksharing directives for SIMD instructions—that the final code remains portable, that is, the addition of accelerated code does not interfere with the standard compilation of the code on commodity hardware using standard nonaccelerating compilers. Third, since the RI-MP2 method alongside other, more advanced noniterative many-body methods in CC theory alike (Crawford & Stanton, 1998; Eriksen, Jørgensen, & Gauss, 2015; Eriksen, Jørgensen, Olsen, & Gauss, 2014; Eriksen, Kristensen, Kjærgaard, Jørgensen, & Gauss, 2014; Eriksen, Matthews, Jørgensen, & Gauss, 2015, 2016a, 2016b; Kállay & Gauss, 2005, 2008; Kowalski & Piecuch, 2000; Kristensen, Eriksen, Matthews, Olsen, & Jørgensen, 2016; Kucharski & Bartlett, 1998a, 1998b; Piecuch & Wloch, 2005; Piecuch, Wloch, Gour, & Kinal, 2006; Raghavachari, Trucks, Pople, & Head-Gordon, 1989) are intrinsically reliant on large matrix-vector and matrix-matrix operations, the main need for accelerators is for offloading exactly these. Thus, besides a number of small generic kernels, for example, tensor permutations or energy summations (as in the present context), compiler directives are primarily used for optimizing the data transfers between the host and device(s), for instance by overlapping these with device computations. Hopefully, the generality of the discussion in the present chapter will encourage and help others to accelerate similar codes of their own.
Finally, one particular potential area of application for the present implementation deserves a dedicated mentioning. While the discussion of the RI-MP2 method herein has been exclusively concerned with its standard canonical formulation for full molecular systems, we note how the method has also been formulated within a number of so-called local correlation schemes, of which one branch relies on either a physical (Ishikawa & Kuwata, 2009; Kobayashi, Imamura, & Nakai, 2007; Mochizuki et al., 2008) or orbital-based (Baudin, Ettenhuber, Reine, Kristensen, & Kjærgaard, 2016; Eriksen, Baudin, et al., 2015; Friedrich, 2007; Friedrich & Dolg, 2009; Guo, Li, & Li, 2014; Guo, Li, Yuan, & Li, 2014; Kristensen, Ziółkowski, Jansík, Kjærgaard, & Jørgensen, 2011; Ziółkowski, Jansík, Kjærgaard, & Jørgensen, 2010) fragmentation of the molecular system. In these schemes, standard canonical calculations are performed for each of the fragments before the energy for the full system is reduced at the end of the total calculation. Thus, by accelerating each of the individual fragment (and possible pair fragment) calculations, the total calculation will be accelerated as well without the need for investing additional efforts, and the resulting reduction in time-to-solution hence has the potential to help increase the range of application for these various schemes.