Chapter 4
Count on It: Number and Quantity
IN THIS CHAPTER
Brushing up on integers
Rewriting fractions and mixed numbers
Determining decimal and percent forms of numbers
Looking at number lines and the order of operations
Figuring out quantities
A good review of math begins with the basics of numbers and the major operations you do with them. The Praxis Core exam involves the basic operations, as well as more complicated ones, using different types of numbers. About 30 percent of the 56 math questions on the exam fall into the “number and quantity” category (that’s about 17 questions if you haven’t warmed up your math muscles yet). Plus, you have to understand these basics in order to perform more complicated math problems.
If you were reviewing how to ride a bike, you might want to start with a discussion of pedals and tires and how to make them move. Doing math is like riding a bike, and this chapter starts at the beginning of your ride down the road to complete preparation for Praxis Core math.
You will have an on-screen calculator to use when you take the Praxis Core exam.
Working with Integers: Whole Numbers and Their Opposites
Think about the first numbers you ever learned. The first numbers you named belong to the most basic category of numbers — whole numbers. They begin with 0 and go on forever: 1, 2, 3, and so on. Each whole number is separated from the next by a quantity of 1. Partial numbers — that is, fractions such as 
and decimals such as 0.4 — are not whole numbers.
All whole numbers other than 0 are positive, which means that they’re greater than 0. A number with no sign before it is understood to be positive. All numbers less than 0 are negative and are represented with a minus sign (–). Every negative number is the opposite of a positive number, and vice versa. For example, the opposite of 8 is –8, and the opposite of –12 is 12.
The integers are all the whole numbers and their opposites. In other words, all the whole numbers and all the negatives of whole numbers make up the entire set of integers. The only integer that doesn’t have an opposite is 0. Poor thing.
Doing basic operations with integers
The basic operations you can perform with integers are addition, subtraction, multiplication, and division. You can perform the same operations with all numbers, but this part of the review focuses on integers because they’re the best numbers to use in the early part of your math review. After all, they’re basic numbers, and this discussion is about basic operations. They make a good fit, basically.
To add or subtract integers, it may help to understand absolute value, which is an integer’s positive distance from 0. The absolute value of any integer is its value without a negative sign. So, the absolute value of any positive integer is the number, and the absolute value of any negative integer is its opposite, or the integer that remains when you drop the negative sign. The 
symbols represent absolute value. Here are a couple examples:
- The absolute value of a positive number:
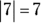
- The absolute value of a negative number:
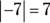
Recall a few facts about working with integers:
- Subtracting an integer is the same as adding its opposite, and adding an integer is the same as subtracting its opposite.
- If an even number of negative integers are multiplied or divided, the product is positive. If an odd number of negative integers are multiplied or divided, the product is negative.
- To add two integers with the same sign, add their absolute values and give the sum the sign that both numbers have.
- To add two integers with opposite signs, subtract the smaller absolute value from the greater absolute value and give the difference the sign of the number with the greater absolute value.
Find the product of the following: 
(A) –48
(B) 24
(C) 48
(D) 25
(E) –24
The correct answer is Choice (C). The product of the absolute values of the integers is 48. Because the number of negative integers in the problem is four (
, and –2), an even number, the product is positive.
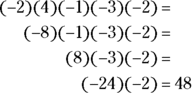
Therefore, the answer is 48.
No matter how well you understand a mathematical concept or process, the threat of careless errors exists. To help avoid them on the Praxis Core exam, make sure you work every step, talk the problem out in your head as you work it, and, if you have time, go back over all the problems you worked after you reach the end of the math section. Danger lurks in the shadows, so be careful out there!
Finding factors of whole numbers
A factor of a whole number is a whole number that can be divided into it a whole number of times. For example, 4 is a factor of 20 because 4 can be multiplied by the whole number 5 (which is also a factor of 20) to get 20. The number 4 is not a factor of 21, 19, or any other number that is not evenly divisible by 4. And if you can break down a number’s factor even further into its own factors, those smaller factors are also factors of the original number you started with. For example, because 2 is a factor of 4, 2 is also a factor of 20.
Every whole number has itself and 1 for factors. If those are the only two factors of a number, it’s a prime number. For example, 3, 17, 31, and 79 are prime numbers.
To determine the factors of a number, first determine one factor and what it has to be multiplied by to get the number. Then find factors of those numbers the same way. Continue the process until no numbers can be broken down further. At this point, you’ve found the prime factorization of the number — a representation of the number as a product of all its prime factors. From there, all the number’s factors, other than 1, can be found by multiplying every possible combination of the prime factors.
Find all the factors of 30.
(A) 30 and 1
(B) 2, 3, and 5
(C) 1, 2, 3, 5, 6, 10, 15, and 30
(D) 2, 3, 5, 6, 10, and 15
(E) 2 and 15
The correct answer is Choice (C). All the numbers listed are either prime factors of 30, products of combinations of those prime factors, or 1. However, Choice (C) is the only choice that includes all of them.
Employing some helpful divisibility rules
Knowing the divisibility rules concerning single-digit numbers and 10 can be helpful for finding factors of numbers. Check out Table 4-1.
TABLE 4-1 Divisibility Rules
A whole number is divisible by … |
… if … |
Examples |
0 |
No number is divisible by 0. |
Sorry; nothing to see here. |
1 |
All whole numbers are divisible by 1. |
Every whole number is an example of this rule. |
2 |
The last digit is an even number (0, 2, 4, 6, 8). |
12; 728; 4; 962 |
3 |
The sum of the digits of the number is divisible by 3. |
27 ( |
4 |
The last two digits form a number that’s divisible by 4. |
124 (24); 736 (36); 13,112 (12) |
5 |
The last digit is 0 or 5. |
25; 360; 40; 195 |
6 |
The number is divisible by both 2 and 3. |
12; 54; 270; 906 |
7 |
You can double the last digit and subtract it from the rest of the number to get either 0 or a number with an absolute value that’s divisible by 7. |
14; 63; 175; 707 |
8 |
The last 3 digits form a number that’s divisible by 8. (This rule, of course, is useful only with numbers with more than three digits.) |
2,800; 16,384; 596,656 |
9 |
The sum of the digits is divisible by 9. |
18; 72; 108; 918 |
10 |
The last digit of the number is 0. |
100; 810; 21,370 |
); 138 (
); 10,011 (
)Finding multiples of integers
A multiple of a number can be obtained by multiplying the number by an integer. For example, multiples of 5 include 5, 10, 15, 20, 25, and so forth. The phrases a multiple of and divisible by have basically the same meaning, but divisible by generally refers specifically to whole numbers, while multiple is used to label whole numbers as well as other types of numbers. If an integer is evenly divisible by another integer, it’s automatically a multiple of it.
Each of the following is a multiple of 3 EXCEPT
(A) 96
(B) 123
(C) 3,000
(D) 761
(E) 903
The correct answer is Choice (D). By using the divisibility rule for 3 (see Table 4-1), you can determine that 96, 123, 3,000, and 903 are divisible by 3. The digits of each number add up to a number that’s divisible by 3. That means each one is a multiple of 3 because you can multiply 3 by another integer to obtain each number. However, the digits of 761 add up to 14, which is not divisible by 3. You can also use long division to determine whether each number is a multiple of 3 by seeing whether 3 goes into it a whole number of times, but that takes longer. Fortunately, you can use a calculator to save time.
Determining the greatest common factor and least common multiple
Two whole numbers can have factors in common. Such factors are called common factors. The greatest of those factors is the greatest common factor of the two numbers. To find the greatest common factor of two numbers, find all the factors of both numbers, determine which factors the numbers have in common, and then determine which of those common factors is the greatest (largest).
For example, to determine the greatest common factor of 20 and 45, you must first determine the factors of both numbers. You can use the prime factorization technique to find them.
- 20: 1, 2, 4, 5, 10, 20
- 45: 1, 3, 5, 9, 15, 45
What factors do 20 and 45 have in common? The common factors are 1 and 5. Because 5 is the greatest of the common factors, 5 is the greatest common factor.
The least common multiple of two numbers is like the greatest common factor, except that it’s the lowest number instead of the highest one, and it’s a multiple instead of a factor (as well as positive). To find the least common multiple of two numbers, write out several multiples of each and then determine the lowest multiple that they have in common.
For example, to find the least common multiple of 3 and 5, first write multiples of both numbers until you see one that they have in common.
- 3: 3, 6, 9, 12, 15, 18, 21
- 5: 5, 10, 15
For 5, you can stop at 15 because 15 is also a multiple of 3. Because 15 is the lowest of the multiples that 3 and 5 have in common, 15 is the least common multiple of 3 and 15.
You can’t just multiply the factors together to get the least common multiple. Multiplying the factors will give you a common multiple, but it may not be the smallest one. For example, if you want the least common multiple of 4 and 6, you can’t multiply them because that gives you 24, when the least common multiple is actually 12.
Exponents and square roots
Have you ever taken a shortcut? If so, you’re not alone, and you can relate to the idea of using exponents to represent multiplication. The people who invented the language we use to represent numbers decided to use shortcuts in representing multiplication involving a factor more than once. Imagine reading and writing stuff like this all the time:
Fortunately, an easier way was created. In the preceding example, 7 is multiplied 21 times. That 21 can be used as an exponent:
An exponent represents how many times a number is a factor. A number with an exponent is said to be set to that power. 721 is “7 to the 21st power,” for example. On the Praxis Core exam, you’re almost guaranteed to see exponents. You may also see two very common exponents. When a number has 2 for an exponent, the number is squared, which means the number is multiplied by itself. When a number has an exponent of 3, the number is cubed, or multiplied by itself two times.
- 52 is “5 squared” (
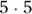), or 25. - 103 is “10 cubed” (
), which equals 1,000.
Math questions on the Praxis Core exam can involve numbers with exponents as parts of larger operations, but they can also ask you flat out what the value of a number with an exponent is.
Which of the following numbers is 4 cubed?
(A) 16
(B) 
(C) 43
(D) 64
(E) 256
The correct answer is Choice (D). 4 cubed is 43, which represents 
. The value of 
is 64.
Often in math, if you can ride one way down a road, you can turn around and ride the other way. As you can find the value of the square of a number, you can find what has to be squared to get a number. What you have to square to get a number is the number’s square root. For example, the square root of 81 is 9 because 9 squared (
) is 81. The symbol for square root is 
. The number you are taking the square root of goes inside the symbol.
represents “the square root of 9.” The positive number that is squared to get 9 is 3, so the square root of 9 is 3. Thus, 
because 
.
What is the value of 
?
(A) 36
(B) 6
(C) 1,296
(D) 72
(E) 18
The correct answer is Choice (B). The positive number that is squared to get 36 is 6; 
. Choice (A) is incorrect because 36 is simply the number in the square root symbol. Choice (C) is false because 1,296 is 36 squared. Choice (D) is the product of 36 and 2. Choice (E) is the value of 
and also the value of 
, but it’s not the square root of 36.
Computing with Fractions and Mixed Numbers
Not all numbers are whole. Fractions represent partial numbers and are represented through the use of integers. The integer on top is the numerator, and the integer on the bottom is the denominator. In the fraction 
, 3 is the numerator and 4 is the denominator. What the fraction represents is “3 out of 4.” If 3 of the people in a rock group have music degrees, and the band has 4 members, 
of the members of the band have music degrees. A fraction also represents a ratio, which is a comparison of two quantities. The fraction 
, for example, represents the ratio “3 to 4.”
If you eat a whole pie and 
of another one, the number of pies you eat can be represented by a mixed number, 
. A mixed number is an integer followed by a fraction. Every mixed number represents a fraction with an absolute value that is greater than 1.
A fraction also represents division. The numerator is divided by the denominator. Every integer is understood to be over 1. For example, 
.
Simplifying fractions
Different fractions can have equal values. The fractions 
and 
represent the same amount, for example. They both represent half. If 20 out of 50 people vote for a political candidate, 2 out of every 5 people vote for the candidate. The difference is that a group of 50 people involves multiple sets of 5 people, while a group of 5 people does not. It only involves 1. The fraction 
is simplified, which means it cannot be written with two integers with smaller absolute values. It is written in the simplest form possible.
To simplify a fraction, you find the greatest common factor of the numerator and the denominator, and then write the number of times the greatest common factor goes into each. The greatest common factor of 20 and 50 is 10. To simplify 
, write the number of times 10 goes into 20 and write it over the number of times 10 goes into 50.
Using any common factor will lead you in the right direction. If you don’t use the greatest common factor, however, you’ll have to repeat the process of finding common factors and simplifying the fractions until they can’t be simplified anymore.
Which of the following represents 
in simplest form?
(A) 
(B) 
(C) 
(D) –6
(E) 
The correct answer is Choice (A). The greatest common factor of 18 and 24 is 6, which goes into 18 three times and 24 four times. The simplest form of the fraction is therefore 
. Choice (B) is another form of the fraction, but not the simplest form. If you arrive at such an answer, you must continue to look for common factors. Choice (C) results from multiplying the numerator and denominator by 2, and Choice (D) is the result of subtracting 24 from 18. Choice (E) is the result of dividing only the numerator by the greatest common factor.
Knowing how to simplify fractions is important because answers that are the results of operations with fractions must always be in simplest form unless otherwise indicated.
Converting between fractions and mixed numbers
Mixed numbers can be written as fractions. Knowing how to write mixed numbers as fractions is important when you perform operations with mixed numbers, and writing fractions as mixed numbers is necessary if your answer choices on the Praxis Core exam are mixed numbers.
To write a mixed number as a fraction, multiply the denominator of the fraction by the absolute value of the integer. Then add the numerator to that product. Write the result over the denominator of the fraction.
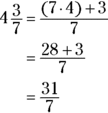
Put a negative sign before the fraction if the mixed number is negative.
To go the opposite way down that road and convert a fraction to a mixed number, write the highest integral (the adjectival form of integer) number of times the denominator fits completely into the numerator. Then write what remains as the numerator of a fraction beside the integer. The denominator of the fraction will be the denominator of the fraction you are converting. The number 7 goes into 31 completely 4 times because 
, which is 3 short of 31.
Performing basic operations with fractions and mixed numbers
Knowing how to convert between fractions and mixed numbers is useful in performing basic operations with them. We highly recommend converting mixed numbers to fractions when performing addition, subtraction, multiplication, or division. Working with fractions is much easier than working with mixed numbers.
Adding and subtracting fractions
To add fractions with the same denominator, add the numerators and write the sum over the denominator both fractions have, which is called the common denominator. If you add two apples and three apples, you get five apples. Similarly, if you add two sevenths and three sevenths, you get five sevenths.
Now, what do you do if you want to add two fractions that don’t have the same denominator? You turn them into two fractions that do have the same denominator, by force. The way to do that is to write at least one of the fractions in a different but equal form. Usually, you need to convert both fractions into new forms. To convert fractions into new forms, you can multiply the numerator and the denominator by the same number, which should be the number you have to multiply by to get the denominator you want.
Any common multiple of the denominators of fractions will work as a common denominator, but the best common denominator to use is the least common multiple. If you use another common denominator, you’ll have to simplify the sum of the fractions. A guaranteed way to find a common multiple of two numbers is to multiply them by each other. However, this does not always result in the least common multiple. It only guarantees a common multiple, not necessarily the smallest one.
You follow the same procedure to subtract fractions, except you, well, subtract. That’s the only difference.
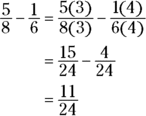
Multiplying fractions
To multiply fractions, multiply the numerators and then multiply the denominators. Write the product of the numerators over the product of the denominators.
Unless otherwise suggested, all fractions that are final answers must be in simplest form.
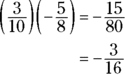
Dividing fractions
Dividing by a fraction is the same as multiplying by its reciprocal, which is what you get when you switch the numerator and denominator of a fraction.
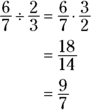
The fraction 
is an example of an improper fraction, which is a fraction in which the numerator is greater than the denominator. Improper fractions make acceptable answers as long as they’re simplified and the correct one is among the choices you are given.
Working with mixed numbers
To perform the basic operations with mixed numbers, convert them to improper fractions and then perform the operations as you would with any fractions, as shown in the following examples:
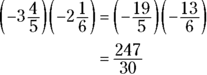
If every section of each box is the same size, what is the sum of the fractions of the boxes that are shaded?
© John Wiley & Sons, Inc.
(A) 
(B) 
(C) 
(D) 
(E) 
The correct answer is Choice (B). The fraction of the first box that is shaded is 
, and the fraction of the second box that is shaded is 
. The sum of those two fractions is 
. Choice (A) is the reciprocal of the answer, Choice (C) is the result of adding the unshaded fractions of the boxes, and Choice (D) is the numerator of one fraction over the sum of the fractions’ denominators. Choice (E) is the simplified form of Choice (D).
Working with Decimals and Percents
Now the review comes to one of the most famous types of fractions — the percent. A percent is a representation of a number of hundredths, and it’s represented by the symbol %. The % sign and the word “hundredths” have the same meaning. Their meanings are 100% the same. A percent greater than 100% represents a quantity greater than 1.
Percents are related to decimals. Decimals represent whole and partial numbers. Both 0.17 and 64 are decimals. In 64, the “.0” is implied. Decimals can be written as percents, and percents can be written as decimals. Both can be written as fractions. Techniques can be used for converting numbers from any one of those forms to either of the other two. (Note that the word decimal refers to both the punctuation mark and numbers that use the punctuation mark but not a %.)
Converting between decimals and percents
Percent means “per centum” or per 100 (divided by 100).
A fraction represents division. The numerator is divided by the denominator.
Dividing the numerator by the denominator will change the fraction to decimal form.
When you divide by 100, you move the decimal two places to the left. So, when working with percents, you want to be skillful at moving between whole numbers, fractions, and decimals.
Looking at the example below, you will note that changing a decimal to its equivalent percentage requires multiplying by 100. Decimals can be written as percentages by moving the decimal point two places to the right and including the percent sign.
So multiplying by 100 and dividing by 100 undo each other. It’s like taking a step forward and taking a step back.
Which of the following percents is equal to the fraction 
?
(A) 60%
(B) 30%
(C) 35%
(D) 65%
(E) 
The correct answer is Choice (A). When dividing 3 by 5, you get 0.6. If you move the decimal two places to the right and add a percent sign, you get 60%. Choices (B), (C), and (D) involve miscalculations, and Choice (E) results from the false method of simply adding a percent symbol.
Performing basic operations with decimals
Doing the basic operations with decimals isn’t very different from doing the same operations with integers. The only major difference is that decimal placement has to be taken into account. Beyond that, everything is pretty much the same.
Adding and subtracting decimals
To add or subtract decimal numbers, line up the decimal points (even the one in the answer) and then add the numbers as if they were integers. Digits with nothing under them can be dropped, though some may have digits carried over them that need to be added. Also, after the last non-zero digit after a decimal point, you can add as many 0s as you want, though it’s not a requirement. Doing so doesn’t change the value of the number.
Multiplying decimals
You multiply decimals exactly the same way you multiply integers, except the total number of digits after the decimal point in the answer equals the number of places after the decimal points in the numbers you’re multiplying. So, if you have a total of three places after the decimal points in the numbers you’re multiplying, you need to have three digits after the decimal point in your answer.
Don’t line up the decimal points if they don’t happen to already be lined up when you align the numbers to the right, unless you want to confuse yourself.
Dividing decimals
To divide with decimals, you can use long division the way you would with integers. However, you move the decimal in the number being divided as many places to the right as you need to in order to get an integer. To make up for the change, you move the decimal in the number it is divided into the same number of places to the right. Then, you bring the decimal in the number in the division box to the top of the box, right above the decimal inside the box.
is the same as 
. If you put the decimal in the answer directly above the decimal in 30576.8, you can divide as you would without the decimal. Just remember where the decimal belongs in the answer, which is 3.7.
Keep in mind that a calculator is available for you to use when you take the Praxis exam.
Understanding the Number Line
The number line is a tool that’s used to illustrate orders of numbers. The numbers represented on it can vary. On all versions of the number line, numbers decrease to the left and increase to the right. Although only a few numbers are shown in any given instance, the numbers represented by suggestion are all the real numbers. The arrows indicate that the numbers go on infinitely in both directions.
© John Wiley & Sons, Inc.
Interpreting numeration and place values
The numbers represented by points on the number line are coordinates. The points are named not only by their coordinates, but also sometimes by letters that appear above the points. The coordinate of Point C could be 4, for example. The point can also be called 4.
Questions on the Praxis Core exam may go beyond identifying points by the numbers under them. Questions can involve distances, and those questions are rooted in placements of coordinates.
Point C is not labeled, but it is halfway between Points A and D. What is the distance from Point C to Point D?
© John Wiley & Sons, Inc.
(A) 4
(B) 3
(C) 5
(D) 2
(E) 7
The correct answer is Choice (A). Since the coordinate of Point A is –1 and the coordinate of Point D is 7, the distance between them is 8. Half of that distance is 4, and 3 is 4 units from both –1 and 7. Choice (B) is the coordinate of Point C. Choice (C) is the coordinate of the point that is halfway between Points C and D. Choice (D) is the distance from one labeled coordinate to the next, and Choice (E) is merely the coordinate of Point D.
The number that’s halfway between two numbers is the average of the two numbers. Recall that the average of a group of numbers is the sum of the numbers divided by the number of numbers in the group.
Knowing the basics of order
The number line can be helpful for putting numbers in order. A question about order on the Praxis Core exam can involve differing types of numbers. For example, an order question can involve a mixture of integers, fractions, mixed numbers, and decimal numbers. The best way to put such an assortment of numbers in order is to rewrite all of them as one type of number, such as all fractions or decimals. Then you can use the number line as a mental and visual aid to put the numbers in order.
Suppose you need to put the numbers 2.78, 
, 2, and 
in order from least to greatest. You can put all these numbers in improper fraction form and get a common denominator, but it may be easier to convert all the numbers to decimal form.
Because the order of the decimal forms is 2.0, 2.5, 2.666…, 2.78, the order of the numbers as given is 2, 
, 
, 2.78. Placing the decimal form numbers on the number line, or at least thinking about where they are on the number line, can help put the task into focus.
The number line can also be useful for addition and subtraction problems that involve negative numbers. Left is the negative direction, and right is the positive direction.
Finding orders of magnitude
The magnitude of a number is its absolute value, or positive distance from 0. A question on the Praxis Core exam can involve the order of the magnitudes of numbers. To find the answer to this type of question, just drop all negative signs that may be involved and put the remaining numbers in order.
Determine which answer choice has the following numbers in order of magnitude from least to greatest: 9, –2, 5.7, 
.
(A) 
, –2, 5.7, 9
(B) 9, 5.7, -2, 
(C) 9, 
, 5.7, –2
(D) –2, 5.7, 
, 9
(E) 
, 9, 5.7, –2
The correct answer is Choice (D). Without the negative signs, the order of the numbers from least to greatest is –2, 5.7, 
, 9, so that is the order of magnitude from least to greatest. Choice (A) is the order of the numbers from least to greatest without magnitude taken into account, Choice (B) is the actual order of the numbers from greatest to least, and Choice (C) is the order of magnitude of the numbers from greatest to least. Choice (E) has no excuses for itself.
Finding numbers in sequences
A sequence is a list of numbers in a certain type of order. Have you ever heard a person talk about doing something in sequence? It means doing the parts of the task in order. Sequences are important because many types of orders of numbers exist. For example, a sequence can be a list of prime numbers in which order increases. One of the most common classifications is the arithmetic sequence, in which the same quantity is added to each number to get the next. In the following arithmetic sequence, 4 is added to each number to determine the next number.
3, 7, 11, 15, 19, 23, 27…
Another is the geometric sequence, for which each number is multiplied by the same quantity to get the next.
2, 6, 18, 54, 162, 486…
On the Praxis Core exam, you may be asked to determine a number that should appear in a certain position in a sequence. To make the determination, first decide what is done to each number in order to create the value of the one that follows. Then, make the calculation for each number up to the position in question.
What is the ninth term of the following sequence? 3, 6, 12, 24, 48…
(A) 96
(B) 2,304
(C) 768
(D) 72
(E) 1536
The correct answer is Choice (C). The sequence is geometric, so each term must be multiplied by 2 to result in the next. The fifth term is 48, so it must be multiplied by 
for the multiplication to result in the ninth term of the sequence, which is 768. Choice (A) is the sixth term, Choice (B) is the square of 48, and Choice (D) is the sum of 48 and 24. Choice (E) is the tenth term of the sequence.
Following Orders: The Order of Operations
After you have the basic mathematical principles down, you’re ready to tackle the order of operations.
When multiple computations are involved in finding a value represented by multiple numbers and operations signs, the rules concerning the order in which the operations are to be worked must be applied. Doing them in the wrong order can cause answers to be false, which is not the ideal situation. To avoid such examination misfortune, you must follow the order of operations, or the correct procedure for working multiple computations.
Think about how you would determine the value of the following expression:
What would you do? Hold that thought. We have an idea.
Remembering “GEMDAS”
The acronym “GEMDAS” is formed by the initials of the order of operations, in order:
- G: Grouping symbols (such as parentheses, brackets, and fraction bars)
- E: Exponents
- MD: Multiplication and Division in order from left to right
- AS: Addition and Subtraction in order from left to right
Notice that multiplication and division are represented together, as are addition and subtraction. That indicates that you must do those operations in the order in which they appear. For example, you don’t want to add all the way from left to right and then go back and do all the subtraction from left to right.
Okay, we believe an unresolved issue is still waiting for an answer. How do you find the value of 
? Well, the first step is to find the value within the grouping symbols, the parentheses. Then the exponent needs to be used. Next comes the indicated multiplication, and then the addition.
Using the order of operations within itself
What should you do if the issue of operations order arises within a step of the order of operations? Don’t worry. The order of operations is a principle of its word. It applies even within steps of itself. If multiple operations are needed within parentheses, for example, apply the order of operations inside the parentheses.
(A) –52
(B) 22
(C) 52
(D) 152
(E) 192
The correct answer is Choice (C). The value within the parentheses must be determined first, and then it must be squared because exponents come next in the order of operations. The product of 2 and 5 should be added to the value. At this point, the value within the brackets can be determined. Then, you need to find the product of 4 and 6 and add it to the result of subtracting 7 from the value within the brackets. Here’s how the math looks when you work it out:
Reasoning with Quantities
The Praxis Core exam tends to involve questions about quantities and how they are related. Various categories of quantities exist, and two major systems are used for measuring them.
Using the two major systems of measurement
The two mainstream systems of measurement in the United States are the English system and the metric system. Table 4-2 shows the basic units of measurement for each system.
TABLE 4-2 Systems of Measurement
Form of Measurement |
English System |
Metric System |
Distance |
Inch, foot, yard, mile |
Meter |
Volume |
Cup, pint, quart, gallon |
Liter |
Weight |
Ounce, pound, ton |
Gram |
The metric system has fewer units because each category of measurement uses the same base unit. However, you can add prefixes to the unit that give you more specific information about the size of the measurement. For example, 1,000 grams is the same as 1 kilogram. All the prefix meanings in the metric system are multiples of 10 or multiples of 
. Check them out in Table 4-3.
TABLE 4-3 Metric System Prefixes
Metric Prefix |
Meaning |
Milli- |
|
Centi- |
|
Deci- |
|
Main unit (meter, liter, gram) |
1 |
Deca- |
10 |
Hecto- |
100 |
Kilo- |
1,000 |
The English system doesn’t have consistent base units for categories of measurement. The English units for each type of measurement are based on each other, but not in ways that mere prefixes are sufficient for changing terminology with varying levels. Here’s how the different units of measurement relate within each form:
- Distance: 12 inches = 1 foot, 3 feet = 1 yard, and 5,280 feet = 1 mile.
- Volume: 2 cups = 1 pint, 2 pints = 1 quart, and 4 quarts = 1 gallon.
- Weight: 16 ounces = 1 pound, and 1 ton = 2,000 pounds.
Converting units of measurement
Problems on the Praxis Core exam may involve converting one unit of measurement to another. For example, you may need to determine that 5 feet is the same as 60 inches or figure out how many deciliters are in 3 hectoliters.
To make such conversions, use the more basic unit to divide if the answer involves the bigger unit and multiply if the answer involves the smaller unit. For example, say you want to know how many inches of twine are in 4 yards. You have to convert yards to feet to inches:
Convert yards to feet.
4 yards = 4(3 feet) = 12 feet
Convert feet to inches.
(12)(12 inches) = 144 inches
Therefore, 4 yards is equal to 144 inches.
To convert from greater to lesser units, multiply instead of divide. The same applies to metric units, but the conversions are easier because you can simply multiply by multiples of 10 or 
.
The more involved conversions require what is called dimensional analysis. It is important then to know the units and make sure they align first before performing any calculations. Such as:
Jan is preparing punch for the party. She expects that each guest will drink at least 3 cups. How many gallons does she need to prepare for the expected 15 guests?
First, figure the number of cups; 15 guests would need 15 x 3 cups of drink.
cups
Next, use the conversions for cups to gallons. You have to go from cups to pints to quarts to gallons — unless you already know the relationship between cups and gallons!
So about 3 gallons would be needed. In order to ensure the appropriate numbers are calculated, the conversions have to be set so that units cancel themselves out and you end up with the one unit you want in the numerator. In this instance, cups, pints, and quarts all canceled out. Gallons stood alone.
How many kilograms are in 7 centigrams?
(A) 0.00007
(B) 7,000
(C) 700
(D) 70
(E) 7
The answer is Choice (A). Moving from kilograms to centigrams, the number gets smaller, so multiply 7 by 
for every space the prefixes are apart on the table. Choice (B) falsely involves the result of multiplying 7 by 103 instead of by 
as a factor five times. Choices (C) and (D) involve too few factors and multiplying in the wrong direction. Choice (E) falsely implies that a kilogram is the same as a centigram.
Basic word problems
Conversions with units can be involved in answering word problems, but often they also require performing other operations. You need to memorize the meanings of the units and prefixes for the Praxis Core exam because they won’t be provided. You also need to understand how words used in each system for each type of measurement are connected to each other.
If a cook pours 5 quarts of water out of a 3-gallon container and then another cook takes his place and adds 2 pints of water, how many cups of water are in the container?
(A) 8
(B) 16
(C) 72
(D) 32
(E) 64
The correct answer is Choice (D). The best way to determine the answer is to convert all the measurements to numbers of cups and then calculate the number of cups remaining. You could also convert the measures to numbers of pints and convert to cups on the last step. Five quarts is equal to 5(4) cups; 3 gallons is the same as 3(16) cups; and 2 pints is a measure equal to 2(2) cups. 
, so the answer is 32. Choice (A) is the number of quarts that result, and Choice (B) is the equivalent measure in pints. Choice (C) is the number of cups that would result if all of the mentioned quantities were added, and Choice (E) could be the correct answer if there were 4 cups in a pint instead of 2.
Practice Questions about Number and Quantity
These practice questions are similar to the questions about number and quantity that you’ll encounter on the Praxis.
1. Which of the following is a counterexample to the following statement?
All prime numbers are odd.
(A) 0
(B) 1
(C) 2
(D) 4
(E) 7.5
2. 
(A) –3
(B) 64
(C) 72
(D) 103
(E) 172
3. Which of the following numbers is the lowest?
(A) 
(B) 3.25
(C) 
(D) 
(E) 3.271
4. The following table represents the percentages regarding the favorite movie categories of students at a college attended by 1,000 students. How many students have a favorite movie category that is either drama, comedy, or horror?
Movie Category |
Percent of Students |
Comedy |
26% |
Musical |
11% |
Drama |
22% |
Documentary |
6% |
Horror |
19% |
Science Fiction |
12% |
Other |
4% |
(A) 26
(B) 67
(C) 220
(D) 670
(E) 6,700
5. Each of the following numbers is a common factor of 150 and 300 EXCEPT
(A) 5
(B) 25
(C) 50
(D) 75
(E) 300
Answers and Explanations
Use this answer key to score the practice number and quantity questions in this chapter.
- C. 2. The number 2 is both an even number and a prime number. It’s a prime number because it has exactly two factors — itself and 1. As a matter of fact, 2 is the only even prime number. Choice (A) is incorrect because 0 is divisible by all numbers. Choice (B) isn’t prime because 1 has only one factor. Choice (D) has three factors, 1, 2, and 4. Choice (E) isn’t odd or even because 7.5 is not an integer, and it’s not prime because it isn’t a positive integer.
- C. 72. Follow the order of operations to solve this correctly (remember GEMDAS).
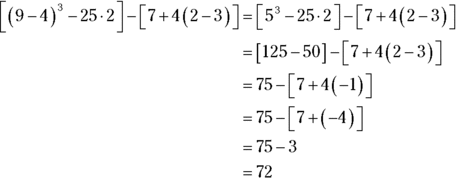
All other answer choices can be reached through following an incorrect order of operations.
- B. 3.25. The best way to determine the answer is to write all the numbers in the same type of form. For example, you can write all the numbers as decimal numbers:
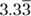, 3.25, 3.50, 3.2357… and 3.271, respectively. The orders of such numbers can be clearer if you give each number the same number of digits after the decimal point. Remember that after the last non-zero digit after a decimal point, you can put as many zeros as you want to. It will not change the value of the number. Then you can put them in order and see that 3.25 is the lowest number, making Choice (B) correct. - D. 670. The sum of the drama, comedy, and horror percentages is 67 percent, and 67 percent of 1,000 is 670. To get 67 percent of 1,000, you can write 67 percent in decimal form by dropping the percent sign and moving the decimal two places to the left. That gives you 0.67, which you can multiply by 1,000 to get 670. Choice (A) is merely the numerical part of the term 26 percent, the percent of students whose favorite genre is comedy. Choice (B) is 6.7 percent of 1,000, Choice (C) is the number of students whose favorite type of movie is drama, and Choice (E) is 670 percent of 1,000.
- E. 300. If you find the prime factorizations of 150 and 300 and use those prime factors to find all the other factors, you can see that Choices (A), (B), (C), and (D) are common factors of 150 and 300. However, 300 is a factor of 300 but not 150, though it is a multiple of 150.