Chapter 5
Introducing Letters: Algebra and Functions
IN THIS CHAPTER
![]() Coming to terms with variables
Coming to terms with variables
![]() Solving equations and inequalities
Solving equations and inequalities
![]() Facing the facts of factoring
Facing the facts of factoring
![]() Making quick work of word problems
Making quick work of word problems
![]() Looking at patterns and conditional statements
Looking at patterns and conditional statements
Now’s the time to revisit your days as an algebra student. When you start treating letters as numbers, you’re entering algebra territory. That’s what this chapter is about. The Praxis Core exam tests basic algebra knowledge, generally the material that’s covered in pre-algebra and perhaps some Algebra I courses, depending on where you went to school and when. Algebra questions make up 30 percent of the math section of the Praxis Core. Also, many of the geometry questions on the test involve algebra, so this chapter goes a long way toward preparing you for the math test of the exam.
Variables: When Letters Represent Numbers
You are very familiar with letters, and algebra just involves using letters in some different ways. Algebra is the area of math that focuses on the basics of working with variables, which are letters that represent numbers. That’s all it is. A large portion of algebra involves determining the numbers represented by variables, which requires knowledge of some basic rules.
The most common letter used to represent numbers is x. Other letters that are commonly used are y, n, a, and b. Most of the letters in our alphabet, and many of the letters in the Greek alphabet, are used as variables at times. But thankfully, you don’t have to know Greek to take the Praxis Core exam.
Here’s an example of using a variable:
This equation means that when 3 is added to some number (x), the result is 7. In this case, the number that the variable x represents is 4. When 3 is added to 4, the result is 7, so x equals 4. Later in this chapter, you review how to determine what a given variable represents. In this section, we cover the basics of variables.
Laying out the terms: Variable terms and expressions
What makes algebra interesting is when variables and numbers meet. When a number comes right before a variable, it means that the number is multiplied by the variable. For example, 3y means “3 times y.” A number can also be multiplied by more than one variable at a time. 10xyz means “10 times x times y times z.” A number that precedes a variable or variables to indicate that it is multiplied by them is a coefficient. In 10xyz, 10 is the coefficient. If no coefficient is given, the coefficient is understood to be 1. In other words, x is the same as 1x, and xyz is the same as 1xyz.
A variable or group of variables next to a coefficient, or with an understood coefficient of 1, is called a term. A number followed by no variables is also a term. In a term, variables can have exponents, which indicate how many times a variable is multiplied (see Chapter 4 for a review of exponents). All of the following are examples of terms:
- x

- 5
- 156abc
- xy
A single term or a group of terms separated by + or – forms an expression. There is no maximum number of terms an expression can have, but the minimum number is one. Yes, a term is an expression, but not all expressions are terms. 48x3y5 is a term, so it is an expression. ![]() has five terms, but it is one expression.
has five terms, but it is one expression.
Let’s get together: Combining like terms
After you’ve come to terms with terms (see the preceding section), it’s time to see how to make them join forces and become one term, when they can. Like terms are terms that have either exactly the same variable or variables with only one exponent for each variable, or no variables.
If two terms are like terms and both have x, y, and z, every x has the same exponent, every y has the same exponent, and every z has the same exponent. Numbers without variables, such as 3 and 5, are also like terms. 17x and 12x are like terms, and so are 15a3b15c8 and 4a3b15c8.
Like terms can be combined. In other words, one can be added to or subtracted from the other to form one term. To combine like terms, combine their coefficients to get a new coefficient and follow that with the common variables and their exponents.
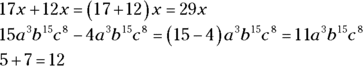
If you have 2 apples and you add 3 apples, you have 5 apples. The same principle works with variables. If you have 2 of x and add 3 of x, you have 5 of x.
Multiplying and dividing with terms and expressions
Just as you can add and subtract terms and expressions (see the preceding section), you can multiply and divide them. Remember that variables represent numbers, which means operations with variables involve the same principles that apply to operations without variables. So, when in doubt, just think about how numbers work.
Multiplying expressions
In multiplying algebraic expressions, the number of times a number or variable is a factor is part of what determines what the product is. To multiply different variables, simply put them next to each other.
To multiply a number times a variable or variables, put them all next to each other.
The next question is what you should do when the same variable is a factor more than once. Do you write the variable next to itself ? Nope. The product has to be written with exponents because a letter times a letter does not equal another letter. The letters have to remain the same, but their exponents do not. The final answer should have exponents representing how many times a variable is a factor.
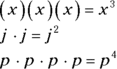
Now put these principles together in your mind, and you’re ready to multiply algebraic terms that have coefficients.
Now, what do you do when the terms you are multiplying have variables with exponents other than 1? For each variable, you just add its exponents.
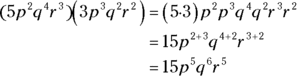
With these skills, you can multiply any algebraic terms. On the Praxis Core, you may be asked to multiply two-term expressions. For example, you may need to multiply ![]() . To find the product of two two-term expressions, the best method to use is FOIL, which is the best-known algebra acronym. It stands for “first, outer, inner, last.” The words apply to the terms in the problem. In this case, the first terms are x and x, the outer terms are x and 3, the inner terms are 2 and x, and the last (as in last in each expression) terms are 2 and 3. To use FOIL, multiply the first, outer, inner, and last terms, and then add their products together (according to the rules for combining terms) in the same order.
. To find the product of two two-term expressions, the best method to use is FOIL, which is the best-known algebra acronym. It stands for “first, outer, inner, last.” The words apply to the terms in the problem. In this case, the first terms are x and x, the outer terms are x and 3, the inner terms are 2 and x, and the last (as in last in each expression) terms are 2 and 3. To use FOIL, multiply the first, outer, inner, and last terms, and then add their products together (according to the rules for combining terms) in the same order.

 Find the following product:
Find the following product: ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
The correct answer is Choice (B). By using FOIL, you can determine that the product of the two expressions is ![]() , which is
, which is ![]() . By combining those terms, you get
. By combining those terms, you get ![]() .
.
You can also find values when entire terms are given exponents. In such cases, the exponent for the term applies to every factor presented in the term.
If a fraction has an exponent, the exponent applies to the numerator and the denominator. That is because you are multiplying the fraction by itself the exponent number of times, and multiplying fractions involves putting the product of the numerators over the product of the denominators.
To raise a power to a power, just multiply the exponents. An exponent shows how many times a factor is a factor. When a factor with an exponent is raised to a power, simply multiply those numbers to get the correct exponent.
The reason is that 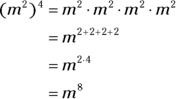 .
.
Dividing expressions
Dividing algebraic terms isn’t as common as multiplying them, but it does happen, so you should know how to perform this operation.
Recall that factors that appear in a term that is a numerator and a term that is the denominator of the same fraction can be cancelled once in both numerator and denominator for every appearance in both. In other words, anything that is a factor of a fraction’s numerator and denominator can be cancelled from both, but it can be cancelled only one time for each instance.
What’s left in the preceding ratio? ![]() , so 4 is left in the numerator. With three x’s on top and two on the bottom, one is left on top because
, so 4 is left in the numerator. With three x’s on top and two on the bottom, one is left on top because ![]() . By the same reasoning, two y’s are left in the numerator. The z’s cancel each other out. Therefore, you’re left with 4xy2.
. By the same reasoning, two y’s are left in the numerator. The z’s cancel each other out. Therefore, you’re left with 4xy2.
Because of this principle, you can easily find the difference of a variable’s numerator and denominator exponents. Just subtract the smaller exponent from the bigger exponent and make the difference the variable’s resulting exponent. Put the variable with that exponent in the place where the bigger exponent was before you subtracted. If a variable in a problem has the same exponent in the numerator and denominator, you can cancel the variable completely. The result of exponent subtraction would be the variable with an exponent of 0, and any value with an exponent of 0 equals 1.

Similarly, when you divide one product of multi-term expressions by another, you can cancel expressions that are factors of both the dividend and the divisor.
Now you’re left with one expression on top and one on the bottom. The quotient is ![]() .
.
On the Praxis Core exam, you may be asked to divide with expressions that have three or more terms. The upcoming section “Factoring in Algebra” shows you how to work such problems.
When variable values are given
The values of expressions can be determined when the values of the variables in them are known. To find the value of an expression is to evaluate the expression. When you evaluate an expression, you replace each variable with its given value. Then you can solve for the value of the expression. Here’s how:
- Replace each variable with its given value.
Follow the order of operations.
Recall GEMDAS from Chapter 4.
- Simplify the resulting expression by following the order of operations as many times as necessary.
- Mark the final number as your answer.
 Evaluate the following expression for
Evaluate the following expression for ![]() ,
, ![]() , and
, and ![]() .
.
![]()
(A) –1
(B) 2
(C) 7
(D) –16
(E) 17
The correct answer is Choice (C). To evaluate the expression, simply replace each variable with its value.
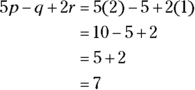
Working with Equations
An equation is a mathematical statement in which one expression is set equal to another. For example, ![]() is an equation. Very commonly in algebra, the value of a variable in an equation can be determined when the value is not given. To determine the value of a variable in an equation is to solve the equation.
is an equation. Very commonly in algebra, the value of a variable in an equation can be determined when the value is not given. To determine the value of a variable in an equation is to solve the equation.
The two sides of an equation have the same value. If ![]() , then
, then ![]() has the same value as 17. The value of n can be determined from the equation.
has the same value as 17. The value of n can be determined from the equation.
Solving for x and other variables
Solving equations is an enormous part of algebra. Understanding how to do it puts you in an excellent position for conquering Praxis Core algebra completely.
To solve an equation, you need to get the variable by itself on one side of the equal sign (=). If you are solving for x, the goal is to work with the equation until you have x = something, like ![]() or
or ![]() . Notice that in both cases, x is by itself on one side of the equal sign and a value is on the other side. Once you reach that point correctly, you have solved the equation. The point of solving an equation is to determine what the variable equals.
. Notice that in both cases, x is by itself on one side of the equal sign and a value is on the other side. Once you reach that point correctly, you have solved the equation. The point of solving an equation is to determine what the variable equals.
To get a variable by itself on one side of the equal sign, you need to perform whatever operations are necessary. Then, if necessary, combine like terms so the variable is in only one term in the equation. The next step is to undo everything that is being done to the variable by doing the opposite. Addition and subtraction are opposite operations, and multiplication and division are opposite operations. You can use opposite operations to undo each other.
Because the two sides of an equation are equal, anything done to one side of the equation must be done to the other side so the two sides will remain equal. If you have a set of weights with 50 pounds on one side and 50 pounds on the other side and you want to add a certain amount of weight to one side, you must add the same amount of weight to the other side to keep the weights of the two sides equal. The values on either side of an equation work the same way. If you add 10 to one side of an equation but not the other, the two sides will no longer be equal. An equation is wrong if its sides aren’t equal.
Here’s how you get a variable by itself to determine its value (also known as solving for x):
Isolate the variable.
Get all the x’s on one side of the equal sign and the numbers without variables on the other side.
Combine like terms.
Add or subtract all the x’s on one side; add or subtract whatever is on the other side of the equal sign.
- Divide both sides of the equation by whatever number (coefficient) is in front of the x (or other variable).
You can see how these steps work by solving for y in this equation: ![]() .
.
Isolate the variable.
Move the y to the left side of the equation by subtracting y from both sides. Move the 12 to the right side by adding it to both sides of the equation. This gives you
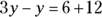 .
.Combine like terms.
Do the operations to get
 .
.Divide both sides of the equation by whatever number (coefficient) is in front of the y.
When you divide 18 by 2, you get 9. Therefore,
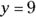 . Problem solved!
. Problem solved!
Undoing addition and subtraction
Consider the equation ![]() . The variable y is not by itself on one side of the equal sign because 4 is being added to y. Getting rid of the addition of 4 will cause y to be by itself on one side of the equation. By subtracting 4, the addition of 4 will be undone. If you add 4 to a number and then subtract 4 from the result, you’re back at the original number. If you have 5 sandwiches and someone gives you 4 sandwiches, and then you give away those 4 sandwiches, you’ll be back to having 5 sandwiches. Algebra works the same way.
. The variable y is not by itself on one side of the equal sign because 4 is being added to y. Getting rid of the addition of 4 will cause y to be by itself on one side of the equation. By subtracting 4, the addition of 4 will be undone. If you add 4 to a number and then subtract 4 from the result, you’re back at the original number. If you have 5 sandwiches and someone gives you 4 sandwiches, and then you give away those 4 sandwiches, you’ll be back to having 5 sandwiches. Algebra works the same way.
|
Original equation |
|
Subtract 4 from both sides to get y by itself on one side. |
|
Determine the value of each side. |
The equation has been solved. The value of y is 5 because ![]() . If you replace y with 5 in the original equation, you will see that the value of y is 5 because
. If you replace y with 5 in the original equation, you will see that the value of y is 5 because ![]() . All solutions to equations can be checked that way.
. All solutions to equations can be checked that way.
Just as subtraction can be used to undo addition, addition can be used to undo subtraction.

In the solution, j is by itself on one side of the equal sign, so the value of j is on the other side of the equal sign. The value of j is 20, so 20 is the solution to the equation. It is true that ![]() , so j is 20.
, so j is 20.
Undoing multiplication and division
Like addition and subtraction (see the preceding section), multiplication and division are opposite operations. When a variable is multiplied by a number, the multiplication can be undone if the term is divided by the same number. Recall that a fraction represents a numerator divided by a denominator. The easiest way to divide a term by a number is to create a denominator with that number. However, you must do this to both sides.

Now m is by itself on one side of the equation. The solution is 6 because that is what m equals.
Because multiplication and division are opposite operations, multiplication can undo division. Think about how to solve the following equation.
The variable, p, is not by itself on one side of the equal sign because it’s being divided by 4. Because you don’t have any addition or subtraction to worry about, you can go ahead and multiply by 4 to undo the division by 4. Multiplying by 4 gets p by itself on one side of the equal sign. The equation is then solved because you’re left with the statement of what p equals.

The solution is 40 because ![]() .
.
Multistep equations
In many algebraic equations, you have to undo more than one operation. The best way to solve such equations is to use whatever addition or subtraction is necessary first and then use multiplication or division.
The following equation requires undoing both multiplication and subtraction. Undo the subtraction first so you can then divide both entire sides by the same number.

The solution is 3 because 3 is what x equals.
Proportions
A proportion is an equation in which one ratio (usually in the form of a fraction) is set equal to another. This is an example of a proportion:
On the Praxis Core exam, you may need to solve one or more proportions in which one term is unknown (represented by a variable). You can save a lot of time by setting the products of the numerator of one ratio and the denominator of the other equal to each other and then cross multiplying. To cross multiply, you multiply the numerator of the left fraction by the denominator of the right fraction, and then you do the same with the right numerator and left denominator. Finally, divide both sides by the coefficient to get the variable by itself and solve the equation.


![]()
For the value of a in the preceding proportion, what is the value of ![]() ?
?
(A) 35
(B) 42
(C) 63
(D) 49
(E) 7
The correct answer is Choice (A). To answer this question, you need to first determine the value of a. By cross multiplying, you get the equation ![]() , the solution to which is 7. Next, substitute 7 in for a in
, the solution to which is 7. Next, substitute 7 in for a in ![]() .
.

The other choices are misleading because all of them are either in the process for finding the correct answer or can result from using a wrong operation. The Praxis Core uses such distractors, so be ready to reason through them. Use your academic street smarts at all times.
Systems of equations
Equations with two variables can be solved if they are accompanied by a second equation with at least one of the variables. When presented with such sets of equations, or systems of equations, the trick is to use the information to get an equation with one variable. Two major methods exist for accomplishing this: the substitution method and the elimination method.
Solving by substitution
The substitution method involves finding the value of one variable in terms of the other in one equation. Then you can substitute that expression for the variable in the second equation. The result is an equation with one variable, and you can solve an equation with one variable by using the earlier discussed techniques.
The concept is that x has the same value in both equations and so does y. To solve the system of equations using the substitution method, you state either what y equals in terms of x or what x equals in terms of y. You can use either equation to make the determination, but the second equation is easier to work with in this case because neither variable has a pesky coefficient.
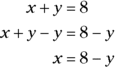
Because x has exactly the same value as ![]() , you can substitute
, you can substitute ![]() for x in the other equation. Then you have an equation with just one variable.
for x in the other equation. Then you have an equation with just one variable.

You can solve the equation to determine that ![]() . Then, you can substitute 5 for y in either equation and solve for x, which is 3.
. Then, you can substitute 5 for y in either equation and solve for x, which is 3.
Solving by elimination
Another method used for solving systems of equations is elimination. It’s based on the fact that adding the same value to or subtracting the same value from both sides of a true equation results in another true equation. In this case, the added or subtracted value is what is represented by both sides of one of the given equations. Check out this example:
Because both sides of the second equation (and the first, for that matter) have the same value, the second equation can be added to the first equation. The result is a third equation that is also true. That’s an ideal thing to do here because adding 3x and ![]() gets rid of x, leaving you an equation with only one variable, y. The coefficients of x have the same absolute value, so elimination can work immediately. You may sometimes have to subtract.
gets rid of x, leaving you an equation with only one variable, y. The coefficients of x have the same absolute value, so elimination can work immediately. You may sometimes have to subtract.

Knowing that ![]() , you can put 7 in for y in either equation to determine that
, you can put 7 in for y in either equation to determine that ![]() .
.
To use elimination when neither variable has coefficients with the same absolute value, you can multiply both sides of an equation by the same number and get a new equation. In some cases, you must do that to both equations. Consider the following equations:
Neither variable has coefficients with the same absolute value, but you can multiply both sides of the top equation by 2 and both sides of the bottom equation by 3 to give j the same coefficient. Then you can subtract one equation from the other and get an equation with one variable.

Now that you know ![]() , you can substitute 4 in for p in either equation and solve for j, which has a value of 3.
, you can substitute 4 in for p in either equation and solve for j, which has a value of 3.
Solving for variables in terms of other variables
The substitution method of solving systems of equations requires finding the value of a variable in terms of another variable. Questions on the Praxis Core could ask you to do only that. You may also be asked to solve for a variable in terms of more than one other variable. Suppose you are given the equation ![]() and you are asked to solve for p in terms of the other variables. You can follow the same procedure you use to solve for a variable in terms of a number. The goal is to get p by itself on one side of the equal sign. What is on the other side of the equal sign will be the value of p.
and you are asked to solve for p in terms of the other variables. You can follow the same procedure you use to solve for a variable in terms of a number. The goal is to get p by itself on one side of the equal sign. What is on the other side of the equal sign will be the value of p.

Since p is by itself on one side of the equation and is not on the other side, the value of p in terms of q and r is on the other side. Notice that the answer could be presented in other forms, such as ![]() and
and ![]() . Those, too, would qualify as correct answers.
. Those, too, would qualify as correct answers.
Solving Inequalities
All men and women are created equal, but not all expressions are. An inequality is a mathematical statement in which one side is (or may be) greater than or less than the other side. Some inequalities also suggest that the sides may be equal.
The signs used in inequalities are
 , which means “less than”
, which means “less than” , which means “greater than”
, which means “greater than” , which means “less than or equal to”
, which means “less than or equal to” , which means “greater than or equal to”
, which means “greater than or equal to”
The following table shows examples of inequalities and what they mean.
|
“ |
|
“ |
|
“ |
|
“8b is greater than or equal to 48.” |
Like equations, inequalities can be solved when they involve only one variable of unknown value. For the most part, you solve inequalities the same way you do equations, but a couple of the rules change. We cover those in the next section.
Following two more rules when solving inequalities
To solve an inequality, you use exactly the same rules you use to solve equations. However, unlike an equal sign, an inequality sign can change directions. Because of this, you must follow two extra rules when you solve inequalities. The sign in an inequality must change direction when either of the following happens:
- Both sides are multiplied or divided by a negative number.
- The sides are switched.
Consider the following:
You have a true inequality. However, what happens when you multiply both sides by a negative number?
The resulting inequality is false; –3 is not less than –7. However, if the sign were to change direction, the resulting inequality would be true.
The example illustrates that when both sides of an inequality are multiplied or divided by a negative number, the sign must change direction.
Now consider what happens when the two sides of an inequality are switched.
It’s true that 3 is less than 7, but 7 is not less than 3. Because the sides were switched, the direction of the sign has to change.
So, 3 is less than 7, and 7 is greater than 3.
Here’s how you would solve this inequality: ![]() .
.
Isolate the term with the variable.
Add 3 to both sides to undo subtracting 3 from 10x.

Combine like terms and simplify each side.
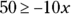 .
.Divide both sides of the equation by whatever number (coefficient) is in front of the x.
Divide both sides by –10 to undo multiplying x by –10.
Simplify each side, and switch the direction of the sign because the sides were divided by a negative number.
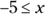
Switch the sides to make x the subject of the sentence, as a formality. Also change the direction of the sign because the sides were switched.
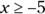
The solution to the inequality is ![]() , which represents –5 and all numbers greater than –5. Any number that is –5 or greater will make the original inequality true.
, which represents –5 and all numbers greater than –5. Any number that is –5 or greater will make the original inequality true.
Graphing inequalities
Inequalities with one variable can be graphed on the number line.
To graph an inequality on the number line, place a circle on the line at the point representing the boundary of the solution. If the number used in the solution is included by the inequality, darken in the circle. This happens when ![]() or
or ![]() is used. When
is used. When ![]() or
or ![]() is used, the number used in the solution only marks the boundary of what makes the inequality true, and it’s not included in the set of numbers that make the inequality true. In those situations, make the circle hollow, not darkened. Next, darken in the part of the number line that includes the solution.
is used, the number used in the solution only marks the boundary of what makes the inequality true, and it’s not included in the set of numbers that make the inequality true. In those situations, make the circle hollow, not darkened. Next, darken in the part of the number line that includes the solution.
For example, if ![]() , a
, a ![]() sign is used, so g can be 3. Therefore, darken in the circle on the number line to show that 3 is included. Then, darken the part of the number line that includes everything greater than 3. If
sign is used, so g can be 3. Therefore, darken in the circle on the number line to show that 3 is included. Then, darken the part of the number line that includes everything greater than 3. If ![]() , x cannot be 4. 4 would only be the boundary for what x can be, so you would not darken in the circle on the number line.
, x cannot be 4. 4 would only be the boundary for what x can be, so you would not darken in the circle on the number line.

© John Wiley & Sons, Inc.
Describing solution steps
We have shown you various types of algebraic statements and how to solve them. Questions on the Praxis Core that require knowledge of how to solve equations and inequalities may not ask for solutions. They may instead ask what steps are involved, with the choices being English descriptions of steps instead of mathematical forms of equations or inequalities. Some questions may ask about the reverse process.
 Sarah correctly solved the equation
Sarah correctly solved the equation ![]() . If she checks her solution which of the following could be the reverse operation of one of the steps used to solve the problem? Select all that apply.
. If she checks her solution which of the following could be the reverse operation of one of the steps used to solve the problem? Select all that apply.
(A) Subtract 7u from both sides.
(B) Divide both sides by 2.
(C) Add 4 to both sides.
(D) Multiply both sides by 2.
(E) Subtract 4 from both sides.
The correct answers are Choices (D) and (E). You can examine the situation by solving the equation and then looking at your steps.
Questions on the Praxis Core may also ask about reversing the steps of random operations performed with variables that are not in equations. The same methodology applies to answering those kinds of questions.

The final step is the equation that states the solution, ![]() . If the process is worked in the reverse, the second step after writing
. If the process is worked in the reverse, the second step after writing ![]() is going from
is going from ![]() to
to ![]() . That is a matter of multiplying both sides by 2 (Choice D). You also see in the fourth step down that 4 is being added to both sides; the reverse would be to subtract 4 from both sides (Choice E).
. That is a matter of multiplying both sides by 2 (Choice D). You also see in the fourth step down that 4 is being added to both sides; the reverse would be to subtract 4 from both sides (Choice E).
Factoring in Algebra
In Chapter 4, we review factoring numbers. Factoring algebraic terms involves the same general concepts, but variables can be involved. On the Praxis Core exam, you may be asked to factor expressions with varying numbers of terms.
Factoring terms out of bigger terms
To factor an expression with more than one term, first see whether you can combine like terms. After that, take the greatest common factor of all the terms and put it on the outside of a set of parentheses. Then write what the factor has to be multiplied by to get each term in the expression. Don’t forget to take signs into account.
An exam question may also ask you about factors of a single term.
 Which of the following is a factor of 90a2b5c3?
Which of the following is a factor of 90a2b5c3?
(A) 90a2b6c3
(B) 80abc
(C) 9a3b
(D) 10ac2
(E) 180a
The correct answer is Choice (D). 10ac2 is the only term listed that can be factored out of 90a2b5c3. To determine this, write out the factorization of 90a2b5c3:
10ac2 is the only factor among the five answer choices because ![]() can be taken out of the factorization.
can be taken out of the factorization.
Choice (A) is incorrect because b6 cannot be factored out of 90a2b5c3 since b6 has an exponent greater than the exponent in b5. Choice (B) is incorrect because 80 is not a factor of 90. Choice (C) is incorrect because a3 is not a factor of a2 since the exponent of a3 is greater. Choice (E) is incorrect because 180 is not a factor of 90. It is a multiple of it.
Using reverse FOIL
While FOIL (first, outer, inner, last) can be used for multiplying two-term expressions, reverse FOIL can take you in the opposite direction from one expression to two-term expressions times each other. It’s a form of factoring.
Many types of expressions that can be factored through reverse FOIL exist, but the ones you’ll typically see on the Praxis Core have three terms and one variable: for example, ![]() .
.
To use reverse FOIL, create two sets of parentheses in which the first terms contain the variable that is squared in the expression you’re factoring, if the expression has only one variable. If more than one variable is in the expression, you’ll need to try combinations of first terms until you find the one that works. Then think of the numbers that can be multiplied to get the final term of the factored expression. One of the combinations will form the last terms (the “L” in FOIL) in the parentheses. If the coefficient of the variable squared is understood to be 1 and the factored expression has one middle term, you have it made. All you have to do is pick the combination that adds up to the middle term coefficient. Otherwise, use trial and error. What matters is that the product of the two-term expressions in the parentheses is the factored expression. You can always test that.
Here’s how the earlier expression would be factored using reverse FOIL:
In some cases, the coefficient of the term with the variable squared will not be 1. With those, the coefficients of the first terms of the factors have to be considered, as in this example:
Decoding Algebra Word Problems
Algebra can be used to represent and figure out situations that are described with words. Variables can be used to represent quantities that are not yet known, and every equation and inequality makes a statement. Using a variable in a mathematical statement can sum up what has been described with words, and mathematical statements with one variable can usually be solved.
Translating English into mathematical language
Whenever you’re given a description of a scenario that involves a number you don’t know, you need to represent that number with a variable. That’s always the first step. If another number isn’t known, it may be possible to represent it by using the same variable by doing something to the variable, such as adding something to it or multiplying it by something. Think about the following description:
7 more than twice a number
The first step in representing the description mathematically is to use a variable to represent the unknown number. Just pick a letter, such as x. Write down how the number is represented so you can keep up with it.
x: the number
Now think about what is being done to the number. The description involves twice the number, which can be represented by 2x. “7 more than” indicates that 7 is added to the amount, so the result is ![]() . “7 more than twice a number” and “
. “7 more than twice a number” and “![]() ” have the same meaning. However, “
” have the same meaning. However, “![]() ” is much easier to use in algebraic equations.
” is much easier to use in algebraic equations.
Algebraic word problems
Algebraic word problems can look complicated, but they simply involve representing a quantity with a variable (see the preceding section), writing a statement about it, solving for the variable, and using the variable’s value to answer the question. Sometimes you have to figure out the values of other numbers after the value of the variable has been determined. Here’s an example of an algebraic word problem:
3 times a number is decreased by 5. The result is 25. What is the number?
To solve the problem, first use a variable to represent the number.
n: the number
Next, write a mathematical statement about the number by translating the word problem into mathematical language. “Decreased by” means “minus (–),” and “the result is” means “equals (=).” So, the word problem can be directly translated into mathematical language with this equation:
From there, you can simply solve the equation. The value of n, the number, is 10.
In some word problems, more than one quantity is described but only one variable needs to be used. These problems work like the one that was just demonstrated, but you need to represent more than one quantity. Let a variable represent one unknown quantity, and let a more detailed expression involving the same variable represent another quantity.
Two consecutive even integers have a sum of 34. What are the integers?
Use a variable to represent one of the integers and use a longer expression to represent the other integer. Because consecutive even integers are always 2 apart, one is 2 greater than the other.
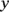 : the first integer
: the first integer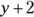 : the second integer
: the second integer
Now just directly translate the word problem into mathematical language. A sum is the result of adding, so add the expressions and show that the result is 34.
You can combine like terms to get the equation ![]() and then solve the equation. In this case,
and then solve the equation. In this case, ![]() , so the first integer is 16 and the second integer is 2 more than that, which is 18. The two integers are 16 and 18. You can check the answer by adding 16 and 18. Their sum is 34.
, so the first integer is 16 and the second integer is 2 more than that, which is 18. The two integers are 16 and 18. You can check the answer by adding 16 and 18. Their sum is 34.
Figuring Out Functions
Functions are generally presented in the form of equations on the Praxis Core. A function may look scary with the f(x) notation at the beginning of the equation, but you have nothing to worry about. If you can solve basic equations, you can solve functions. The following sections give you more details about exactly what a function is and how to solve them.
Identifying functions
In order to understand functions, you need to understand some other basic terminology. To start with, know that a set of ordered pairs is a relation. For example, {(3, 5), (7, 10), (8, –1)} is a relation. It is a set of three ordered pairs. Relations can be represented in other ways. A table is a means of representing ordered pairs by listing x-coordinates next to the y-coordinates with which they are paired. Check out the following table:
x |
y |
–7 |
–2 |
–1 |
4 |
2 |
3 |
5 |
0 |
The table represents the ordered pairs (–7, –2), (–1, 4), (2, 3), and (5, 0).
Relations can also be represented by points on the coordinate plane and by graphs of equations (see Chapter 6 for more on these concepts). The graph of an equation represents an infinite number of ordered pairs.
The set of x values in a relation is the domain, and the set of y values is the range of a relation. Variables other than x and y can be represented by a relation. However, universally, the domain of a relation is the set of the ordered pairs’ first variable values, and the range is the set of second variable values.
Now that you are familiar with the terms relation, domain, and range, you’re ready to see the bigger picture of functions. A function is a relation in which each number in the domain is paired with only one number in the range. Generally, since the first variable of the ordered pairs in a function tends to be x, a function involves x but no repeat of an x value. In other words, each domain value is paired with just one range value, so a value of x never repeats, unless the same range value repeats with it, which is rare. However, a range value can repeat in a function without the same domain value repeating with it.
 Which of the following relations is NOT a function?
Which of the following relations is NOT a function?
(A) {(4, 8), (5, –1), (7, 6), (10, 4)}
(B) {(–2, 7), (–1, 2), (5, –4), (5, –4), (19, 0), (22, 7)}
(C) {(0, 1), (1, 2), (2, 3), (3, 4), (4, 5)}
(D) {(–5, 10), (0, 10), (5, 10), (10, 10)}
(E) {(2, 4), (4, 6), (6, 7), (2, 9), (7, 1)}
The correct answer is Choice (E). The domain number 2 is repeated and paired with both 4 and 9. Thus, 2 is paired with more than one range number. That means that the relation is not a function. Choice (A) is incorrect because no domain number is paired with more than one range number. Choice (B) is incorrect because, although the domain number 5 is repeated, 5 is only paired with –4. Choice (C) is incorrect because, although some numbers are used more than once, no domain number is paired with more than one range number. Choice (D) is incorrect because, although 10 is a range number four times, no domain number is paired with more than one range number.
Working with functions
Functions in the forms of equations often involve ![]() , or another letter followed by x, set equal to an expression that contains
, or another letter followed by x, set equal to an expression that contains ![]() .
. ![]() is pronounced “f of x.”
is pronounced “f of x.”
Consider the equation ![]() . Any value that you put in for x will result in just one value of f(x). A value that is to stand in for x will be represented in the parentheses next to f to show that the value takes the place of x. For the function
. Any value that you put in for x will result in just one value of f(x). A value that is to stand in for x will be represented in the parentheses next to f to show that the value takes the place of x. For the function ![]() , you can determine the value of f(12) by putting 12 in for x in
, you can determine the value of f(12) by putting 12 in for x in ![]() . The result is
. The result is ![]() , or 17. 12 takes the place of x in f(x), so 12 takes the place of x in
, or 17. 12 takes the place of x in f(x), so 12 takes the place of x in ![]() . Understanding that principle is the key.
. Understanding that principle is the key.
Since the letter next to the parentheses is f, the name of the function is f. Letters other than f are often used in function equations. For example, g(x), h(x), and p(x) are commonly used.
 If
If ![]() , what is the value of g(5)?
, what is the value of g(5)?
(A) 5
(B) 8
(C) 28
(D) 25
(E) 3
The correct answer is Choice (C). Because 5 takes the place of ![]() in
in ![]() , 5 takes the place of x in
, 5 takes the place of x in ![]() . Therefore,
. Therefore, ![]() , which is
, which is ![]() , or 28. Choice (A) is just the number that replaces
, or 28. Choice (A) is just the number that replaces ![]() . Choice (B) is the value of
. Choice (B) is the value of ![]() instead of
instead of ![]() . Choice (D) is merely the value of
. Choice (D) is merely the value of ![]() . Choice (E) is just the number that is added to
. Choice (E) is just the number that is added to ![]() in the function.
in the function.
The example involves replacing x with a number. Another possibility is replacing x with something like ![]() . For example, you can find the value of g( f(x)) if you have enough information. Suppose
. For example, you can find the value of g( f(x)) if you have enough information. Suppose ![]() and
and ![]() . To find the value of g( f(2)), first find the value of f(2), and then get g of that number. f(2) is 23, which is 8, so
. To find the value of g( f(2)), first find the value of f(2), and then get g of that number. f(2) is 23, which is 8, so ![]() . Therefore, g(f(2)) is the same as g(8). The value of g(8) is
. Therefore, g(f(2)) is the same as g(8). The value of g(8) is ![]() , or 9. Thus, the value of g(f(2)) is 9.
, or 9. Thus, the value of g(f(2)) is 9.
Thinking Outside the Algebra Box
The information reviewed so far in this chapter covers the basics of working algebra problems, but some of the problems in the Praxis Core math section require basic algebra skills plus an extra degree of critical thinking. Understanding patterns of relationships between quantities and the basic rules of reasoning will help you get the answers to such problems.
Recognizing relational patterns
For some problems, you need to determine how a pattern works and represent it algebraically. This is another example of translating English into mathematical language, but the translating isn’t as direct as it may be in other situations.
If a word problem involves a number of 18-wheeler trucks and the question is how many wheels there are in all, you need to understand that there are 18 wheels for every truck. In other words, the number of trucks multiplied by 18 equals the number of wheels. This is an example of direct variation, which is a relationship pattern in which one quantity increases as another one increases, though they may increase at different rates. Every time a number of 18-wheeler trucks is increased by 1, the number of wheels increases by 18. As one quantity increases, so does the other. The number of wheels increases 18 times faster than the number of trucks. If the number of trucks is represented by x, the number of wheels needs to be represented by 18x.
Inverse variation is a relationship pattern in which one quantity decreases as another one increases. The two quantities don’t increase together, as they do with direct variation. With inverse variation, the greater one quantity is, the smaller the other one is. For example, the amount of time it takes to travel a certain distance decreases with increased rate. Suppose you’re traveling a distance of 10 miles. The faster you travel, the less time it will take. The distance formula is ![]() , in which
, in which ![]() ,
, ![]() , and
, and ![]() . From that formula, it can be concluded that
. From that formula, it can be concluded that ![]() and
and ![]() . The relationship between t and r is one of inverse variation.
. The relationship between t and r is one of inverse variation.
Algebraic reasoning
Some of the math questions on the Praxis Core exam involve conditional statements, also known as “if-then statements.” They state that if one given fact exists, another given fact exists. This is an example of a conditional statement:
If
, then
.
You may be asked whether a certain conditional statement is true. In many cases, you can solve an equation or inequality and then determine whether the conclusion is true. By solving either of the preceding equations, you can determine that ![]() . You can then put 9 in for p in the other equation and see whether the equation is true. In this example, it is. If p did not have the same value in both equations, the statement would be false.
. You can then put 9 in for p in the other equation and see whether the equation is true. In this example, it is. If p did not have the same value in both equations, the statement would be false.
If you’re in doubt about how to figure out the full nature of a conditional statement, there’s an effective method you can use. If you can come up with even one example of a situation where the conditional statement fails, the conditional statement is false. Think about this conditional statement:
If
, then
.
All you have to do is look for one example of a number that makes the statement fail. If you can find any such number, the statement is false. When testing numbers, try using some positive integers, some negative integers, 0, and some fractions between 0 and 1. Sampling those sections of the number line goes a long way toward covering the numerical principles that need to be put to the test. Numbers that make both of the preceding inequalities true include all numbers that are greater than 8, but no number less than –8 works for both inequalities. If you put any number less than –8 in for y, you can see that it doesn’t work. As soon as you find that one exception, you can truthfully conclude that the conditional statement is false.
Practice Questions about Algebra
These practice questions are similar to the algebra questions you’ll encounter on the Praxis Core exam.
1. If ![]() , what is the value of
, what is the value of ![]() ?
?
(A) 17
(B) 107
(C) ![]()
(D) 25
(E) 41
2. If the value of ![]() is the same as the value of
is the same as the value of ![]() , which of the following is equal to
, which of the following is equal to ![]() ?
?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
3. Which of the following is NOT a factor of the product of ![]() and
and ![]() ?
?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
4. Two consecutive even integers have a sum of 42. What is the higher of the two integers?
(A) 20
(B) 26
(C) 18
(D) 24
(E) 22
5. Which of the following is a true statement if ![]() ?
?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Answers and Explanations
Use this answer key to score the practice algebra questions in this chapter.
- A. 17. You can solve the first equation and determine the value of x.
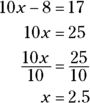
Because the value of x is 2.5, you can substitute 2.5 for x in the expression
 to determine the value of the expression.
to determine the value of the expression. 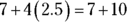 , or 17. Choice (B) is the value of
, or 17. Choice (B) is the value of 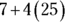 , and 25 is the value of the right side of the equation before you divide both sides by 10. Choice (C) results from subtracting 8 from both sides instead of adding it. Choice (D) is the value of the right side of the equation after you add 8 to both sides. Choice (E) is just wrong.
, and 25 is the value of the right side of the equation before you divide both sides by 10. Choice (C) results from subtracting 8 from both sides instead of adding it. Choice (D) is the value of the right side of the equation after you add 8 to both sides. Choice (E) is just wrong. - C.
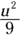 . For problems like this, first think about what can be done to one of the expressions that are stated to be equal to each other in order to get the expression to which one of the choices is equal. In this case, you can square
. For problems like this, first think about what can be done to one of the expressions that are stated to be equal to each other in order to get the expression to which one of the choices is equal. In this case, you can square  to get
to get  . That is a clue that you can try squaring
. That is a clue that you can try squaring  and considering the result.
and considering the result.

- B.
 . First, find the product of
. First, find the product of  and
and 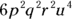 .
.

Next, determine which choice is not a factor of
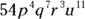 . For
. For  , the variable q has an exponent of 8, which makes
, the variable q has an exponent of 8, which makes 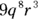 not a factor of
not a factor of 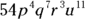 because 8 is higher than the exponent of q in
because 8 is higher than the exponent of q in 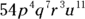 . All the other choices are factors because their coefficients are factors of 54 and they have the same variables with exponents that are whole numbers that aren’t greater than the corresponding exponents in
. All the other choices are factors because their coefficients are factors of 54 and they have the same variables with exponents that are whole numbers that aren’t greater than the corresponding exponents in  .
. - E. 22. You can use x to represent the first integer. Because the next number is the next even integer, it is 2 higher, so you can represent it with the expression
 . The sum of the two consecutive even integers is 42, so you can represent the situation with the equation
. The sum of the two consecutive even integers is 42, so you can represent the situation with the equation 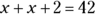 .
.

Because the value of x is 20, the first even integer is 20. The next one is 2 higher, so it’s 22. Choice (A) is the lower of the two integers. The other choices are randomly incorrect.
- C.
 . All of the choices have x followed by an inequality sign and then a number. That is the form of a solution to a single inequality. If you find the solution to the inequality in the question, you can determine which answer choice is a true statement. Solving this inequality involves reversing the sign because you have to divide by a negative number.
. All of the choices have x followed by an inequality sign and then a number. That is the form of a solution to a single inequality. If you find the solution to the inequality in the question, you can determine which answer choice is a true statement. Solving this inequality involves reversing the sign because you have to divide by a negative number.
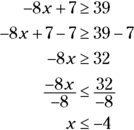
Choice (A) has the < symbol, not the
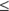 symbol. Choice (B) results from adding 7 to both sides of the inequality instead of subtracting it. Choice (D) results from adding 7 to both sides of the inequality, not changing the direction of the inequality sign when dividing both sides by a negative number, and leaving out the “or equal to” mark. Choice (E) results from not changing the direction of the inequality sign when dividing both sides by a negative number.
symbol. Choice (B) results from adding 7 to both sides of the inequality instead of subtracting it. Choice (D) results from adding 7 to both sides of the inequality, not changing the direction of the inequality sign when dividing both sides by a negative number, and leaving out the “or equal to” mark. Choice (E) results from not changing the direction of the inequality sign when dividing both sides by a negative number.

 Using 1 as an exponent isn’t necessary. A variable without an exponent shown is understood to have an exponent of 1.
Using 1 as an exponent isn’t necessary. A variable without an exponent shown is understood to have an exponent of 1. Whatever you do to a side must be done to the entire side, not just some small part of it. A common mistake is to do something like multiply a term on one side by a number and then multiply just one term among several on the other side by the same number. So not only do you have to do the same thing to each side, but you must do that operation to the complete value of each side to make both sides equal.
Whatever you do to a side must be done to the entire side, not just some small part of it. A common mistake is to do something like multiply a term on one side by a number and then multiply just one term among several on the other side by the same number. So not only do you have to do the same thing to each side, but you must do that operation to the complete value of each side to make both sides equal. Substitution is the ideal method to use when at least one of the variable terms has a coefficient of 1 (understood). Elimination is the generally preferred method to use when both variables have coefficients other than 1 in all cases.
Substitution is the ideal method to use when at least one of the variable terms has a coefficient of 1 (understood). Elimination is the generally preferred method to use when both variables have coefficients other than 1 in all cases.