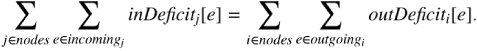A concurrent program terminates when all of its processes have terminated, and similarly a distributed system terminates when the processes at all of its nodes have terminated. The problem posed in this section is to detect a state in which all nodes have terminated. A survey of algorithms for distributed termination can be found in [52]. In this section, we describe an algorithm by Edsger W. Dijkstra and Carel S. Scholten for detecting termination in a distributed system. The presentation follows that in [25], where a preliminary algorithm is developed that is live but not safe, and is then extended to the full Dijkstra–Scholten (DS) algorithm which is also safe.

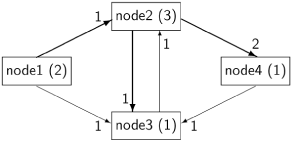
The algorithm collects information from a set of nodes over a period of time in order to decide whether termination has occurred or not. We make one change from the model of distributed computation described in Section 10.1: we do not assume that each node is connected to each other node, only that the set of nodes form a connected directed graph. We do assume the existence of a unique environment node which has no incoming edges and from which every node is accessible by a path through the directed graph. The environment node is responsible for reporting termination. The following diagram shows such a directed graph with four nodes, where node1 is the environment node with no incoming edges:

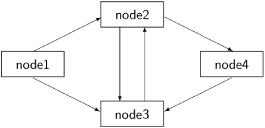
The DS algorithm to detect termination is to be run concurrently with the computation being carried out at each node. The computation sends messages over the edges from one node to another; the DS algorithm specifies additional statements that must be executed as part of the processing of messages by the sender and the receiver. The algorithm assumes that for each edge in the graph from node i to node j, there is a back edge that carries a special type of message called a signal from j to i. The back edges are shown by thick arrows in the following diagram:

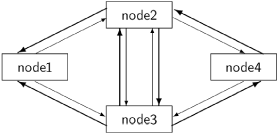
A further assumption is that all the nodes except for the environment node are initially inactive, meaning that they are not performing any computation but are merely waiting to receive messages. The computation of the distributed system is initiated when the environment node sends messages on its outgoing edges. When a node that is not an environmental node receives its first message on any incoming edge, it can begin its computation. Eventually the computation in each node terminates and it will no longer send messages, although if it receives more messages it may be restarted. At all times, a node is able to receive, process and send signals, as required by the termination algorithm.

Under this set of assumptions, we want to develop an algorithm in which the environment node announces termination of the system if and only if the computation has terminated in all the nodes.

Preliminary Algorithm

For each message received by a destination node, it is required to eventually send a signal on the corresponding back edge to the source node. The difference between the number of messages received on an incoming edge E of node i and the number of signals sent on the corresponding back edge is denoted inDeficit_i[E]. The difference between the number of messages sent on outgoing edges of node i and the number of signals received on back edges is denoted outDeficit_i. inDeficit_i[E] must be known for each incoming edge separately, while for outgoing edges it is sufficient to maintain the sum of the deficits over all the edges. When a node terminates it will no longer send messages; the sending of signals will continue as long as inDeficit_i[E] is nonzero for any incoming edge. When outDeficit_env = 0 for the environment node, the algorithm announces termination.

Let us start with a preliminary algorithm (Algorithm 11.1). There are three variables for keeping track of deficits. outDeficit and the array inDeficit[E] were described above. In addition to the array of incoming deficits, the algorithm needs the sum of all these deficits:

No confusion will result if we use inDeficit without an index to represent this sum. (Alternatively, the sum could be generated as needed in send signal.)

There are four parts to this algorithm that must be integrated into the underlying computation of each node:

send message. When the underlying computation sends a message (whatever it is), an additional statement is executed to increment the outgoing deficit.

receive message. When the underlying computation receives a message (whatever it is), additional statements are executed to increment the incoming deficit on that edge, as well as the total incoming deficit.

Table 11.1. Dijkstra–Scholten algorithm (preliminary)

	integer array[incoming] inDeficit ← [0,. . . ,0] integer inDeficit ← 0 integer outDeficit ← 0
send message
p1: send(message, destination, myID) p2: increment outDeficit
receive message
p3: receive(message,source) p4: increment inDeficit[source] and inDeficit
send signal
p5: when inDeficit > 1 or (inDeficit = 1 and is Terminated and outDeficit = 0) p6: E ← some edge E with inDeficit[E] 6= 0 p7: send(signal, E, myID) p8: decrement inDeficit[E] and inDeficit
receive signal
p9: receive(signal, _) p10: decrement outDeficit

send signal. This is an additional process added to the program at each node. The statements of this process may be executed if the condition in the when clause is true; otherwise, the process is blocked. Whenever the incoming deficit is nonzero, the node may send a signal on the back edge, but it does not send the final signal until the underlying computation has terminated and the outgoing deficit is zero. It is assumed that a node can decide if its local computation has terminated; this is denoted by calling the boolean-valued function isTerminated.

receive signal. This is also an additional process that is executed whenever a signal is received; it decrements the outgoing deficit.

For the environment node, the only field needed is the counter for the outgoing deficit (Algorithm 11.2).

Correctness of the Preliminary Algorithm

We now prove that if the computation terminates at all nodes, eventually the environment node announces termination. For the purpose of simplifying the invariants and their proofs, it will be convenient to assume that communications are synchronous, so that every message and signal sent is immediately received; by doing this, we do not have to account for messages that are in transit. Since we are proving a liveness formula with “eventually,” this does not affect correctness, because we have assumed that each individual message and signal is eventually received.

Table 11.2. Dijkstra–Scholten algorithm (env., preliminary)

integer outDeficit ← 0

computation

p1: for all outgoing edges E p2: send(message, E, myID) p3: increment outDeficit p4: await outDeficit = 0 p5: announce system termination

receive signal

p6: receive(signal, source) p7: decrement outDeficit

Notation: inDeficit_i is the value of inDeficit at node i and similarly for outDeficit_i.

Example 11.1. Lemma

At each node i, inDeficit_i ≥ 0 and outDeficit_i ≥ 0 are invariant, as is the equality of the sums of the two deficits over all nodes:

Equation 11.1. 

Proof: Let i and j be arbitrary nodes such that e is the edge from node i to j, and e' is the matching back edge for sending signals from j to i:

Let n be the number of messages received by j on e and n′ the number of signals sent by j on e'; then inDeficit_j[e] = n −n′. But n is also the number of messages sent by node i on e and n′ is also the number of signals received by i on e' so outDeficit_i[e] = n−n′, where the notation outDeficit_i[e] means that we are counting the contribution of edge e to the total outDeficit_i. We have shown that for an arbitrary edge e, inDeficit_j[e] = outDeficit_i[e]. Since each edge is an outgoing edge for exactly one node and an incoming edge for exactly one node, summing over all the edges in the graph gives

Equation 11.2. 

By definition,

Equation 11.3. 

Equation 11.4. 

Substituting (11.3) and (11.4) into (11.2) proves the invariance of (11.1).

For any edge e, inDeficit_j[e] ≥ 0 is invariant, because inDeficit_j[e] is decremented only in send signal and only after explicitly checking that its value is positive. Since outDeficit_i[e] = inDeficit_j[e] for the node j at the other end of e, outDeficit_i[e] ≥ 0 is also invariant. The invariance of inDeficit_i ≥ 0 and outDeficit_i ≥ 0 follows by summing the individual deficits of the edges.

Example 11.2. Theorem

If the system terminates, the source node eventually announces termination.

Proof: The system terminates when the underlying computation terminates at each node; therefore, no more messages will be sent so neither inDeficit_i nor outDeficit_i increase after termination. By the condition in send signal, each non-environment node will continue sending signals until

inDeficit_i > 1 ∨ (inDeficit_i = 1 ∧ outDeficit_i = 0)

becomes false. Using the invariants inDeficit_i ≥ 0 and outDeficit_i ≥ 0 of Lemma 11.1, it can be shown (exercise) that the negation of this formula is equivalent to:

Equation 11.5. 

If inDeficit_i = 0, the formula is true regardless of the truth of outDeficit_i > 0), so this formula is in turn equivalent to:

inDeficit_i = 0 ∨ (inDeficit_i = 1 ∧ outDeficit_i > 0).

From this we deduce inDeficit_i ≤ outDeficit_i as follows: if inDeficit_i = 0 the formula follows from outDeficit_i ≥ 0, while if inDeficit_i = 1, from the second disjunct we have outDeficit_i > 0 which is the same as outDeficit_i ≥ 1.

We have shown that at termination, inDeficit_i ≤ outDeficit_i holds for all non-environment nodes. For the environment node, inDeficit_i = 0 (since there are no incoming edges) and the invariant outDeficit_i ≥ 0 also imply that inDeficit_i ≤ outDeficit_i. Since this holds for all i, it follows from (11.2) that inDeficit_i must be equal to outDeficit_i at all nodes, in particular for the environment node where inDeficit_i = 0. Therefore, outDeficit_i = 0 and the node announces termination.

The algorithm is not safe. Consider the following set of nodes and edges:

Let node1 send messages to both node2 and node3, which in turn send messages to each other. At both nodes, inDeficit_i = 2 and furthermore, inDeficit₂[e2] = 1 at node2 and inDeficit ₃[e3] = 1 at node3. By the statements at p5 and p6 in Algorithm 11.1, both can send signals to node1, which will now have outDeficit_i = 0 and can announce termination although the other two nodes have not terminated.

Let us first consider the case where the directed graph is a tree. In a tree, each node except for the root has exactly one parent node, and furthermore, a tree necessarily has leaves, which are nodes with no outgoing edges. The following diagram shows a tree constructed from our directed graph:

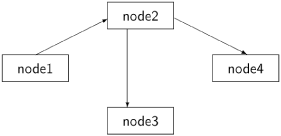
The root is the environment node node1 and the edges are a subset of the edges of the graph. If the graph is a tree, it is trivial to detect termination. When a leaf terminates, it sends a signal to its parent. A non-leaf node waits for signals from each of its children and then sends a signal to its parent. The root has no parent, so when it receives signals from all its children, it can conclude that the distributed system has terminated.

The tree shown in the diagram is called a spanning tree because every node in the graph is included in the tree. The Dijkstra–Scholten algorithm implicitly constructs a spanning tree from the directed graph. By “implicitly,” we mean that the tree is not held in any actual data structure, but it can be deduced from the internal states of the nodes. The trivial algorithm for termination in a tree can then be executed on the spanning tree.

integer array[incoming] inDeficit ← [0,.. . ,0]
integer inDeficit ← 0
integer outDeficit ← 0
integer parent ← −1

p1: when parent ≠ −1        // Only active nodes send messages
p2:   send(message, destination, myID)
p3:   increment outDeficit

p4: receive(message, source)
p5: if parent = −1
p6:     parent ← source
p7: increment inDeficit[source] and inDeficit

p8:  when inDeficit > 1
p9:    E ← some edge E for which
         (inDeficit[E] > 1) or (inDeficit[E] = 1 and E ≠ parent)
p10:   send(signal, E, myID)
p11:   decrement inDeficit[E] and inDeficit
p12: or when inDeficit = 1 and is Terminated and outDeficit = 0
p13:    send(signal, parent, myID)
p14:    inDeficit[parent] ← 0
p15:    inDeficit ← 0
p16: parent ← −1

p17: receive(signal, _)
p18: decrement outDeficit

The source field of the first message to arrive at a node defines the parent of that node. We will call that incoming edge the parent edge of the node. The preliminary algorithm is modified so that the last signal from a node is sent on its parent edge; the parent then knows that no more signals will ever be received from the node. A node sends its last signal only when outDeficit_i has become zero, so it becomes a leaf node in the spanning tree of non-terminated nodes.

The modifications are shown in Algorithm 11.3. The new variable parent stores the identity of the parent edge. The value −1 is used as a flag to indicate that the parent edge is not yet known. send message is modified to restrict the sending of messages to nodes that have already received a message and thus have an edge to their parent nodes. received message is modified to save the parent edge when the first message is received. send signal is modified to make sure that the last signal is sent on the parent edge; signals can be sent along any edge with an outstanding deficit (including the parent), as long as the final signal is saved for the parent node. When terminating, a node resets its parent variable because it may receive new messages causing it to be restarted.

Here a partial scenario:

The first column show the actions: n ⇒ m means that node n sends a message to node m. The other columns show the local data structures at each node: (parent, inDeficit[E], outDeficit). The values of the array inDeficit[E] are shown in increasing numerical order of the nodes. (The variable containing the sum of the values in the array can be easily computed as needed.) The data structures upon completion of this part of the scenario are graphically shown in the following diagram:

The outgoing deficits are shown in parentheses next to the node labels, while the incoming deficits are shown next to the edges.

We leave it as an exercise to expand the scenario to include decisions to terminate, and sending and receiving signals.

when inDeficit > 1
  (E, N) ← selectEdgeAndNum
  send(signal, E, myID, N)
  inDeficit [ E] ← inDeficit [ E] − N
  inDeficit ← inDeficit − N

if  E ≠ parent and inDeficit [ E] ≥ 1
   return (E, inDeficit [ E])
else if inDeficit [ parent] > 1
   return (parent, inDeficit [ parent]−1)

receive (signal, source, N)
outDeficit ← outDeficit − N

integer parent ← 0
integer array [ incoming] inDeficit ← [1, 0,. . ., 0]
integer inDeficit ← 1
integer outDeficit ← 0

The DS algorithm can be difficult to implement if the deficit counts become too large to store in simple integer variables. Credit-recovery algorithms [53, 34] attempt to avoid this problem by using clever representations of the deficits.

In a credit-recovery algorithm, the environment node starts out with a unit “sum of money” or “weight,” W = 1.0. When it sends a message to a node, it “lends” the destination node part of the weight. Non-environment nodes are active if they possess a nonzero amount of weight; in turn, they share this weight when sending messages to other nodes. When a non-environment node becomes terminated, it returns all its weight to the environment node. Once all the weights have been recovered, the environment node can declare global termination.

Algorithm 11.4 is for the environment node. Every outgoing message takes with it half the weight. Once the system has been initialized, the environment node simply waits for the weight that it has lent out to be recovered. This is done by signals sent to the environment node.

Algorithm 11.5 for the non-environment nodes is very similar. A non-environment node starts with zero weight and becomes active when it receives its first message together with an initial weight, which can then be lent to other nodes. When the node terminates, it returns its current weight directly to the environment node.

float weight ← 1.0

p1: for all outgoing edges E
p2:    weight ← weight / 2.0
p3:    send(message, E, weight)
p4: await weight = 1.0
p5: announce system termination

p6: receive(signal, w)
p7: weight ← weight + w

constant integer parent ← 0 // Environment node
boolean active ← false
float weight ← 0.0

p1: if active                   // Only active nodes send messages
p2:    weight ← weight / 2.0
p3:    send(message, destination, myID, weight)

p4: receive(message, source, w)
p5: active ← true
p6: weight ← weight + w

p7: when terminated
p8:   send(signal, parent, weight)
p9:   weight ← 0.0
p10:  active ← false

While we have shown non-environment nodes waiting until they terminate to return their weight, the algorithm could have enabled or required them to return excess weight earlier. For example, in Mattern’s algorithm, weight received while a node is active is immediately returned to the environment node:

receive (message, source, w)
if active then
   send(signal, parent, w)
else
   active ← true
   weight ← w

Just as the deficit counters in the DS algorithm can grow to be very large, the values of weight can grow to be very small. The first node to receive a message from the environment node receives a value of 2⁻¹. If it now sends out one million messages, the values of weight will become 2⁻², 2⁻³, . . . , 2^−1000001. By storing just the negative exponent, this is no more difficult than storing the value 1000000 in outDeficit. The problem arises when arbitrary weights are added in the environment node, leading to values such as: 2⁻¹ + 2⁻¹⁵ + 2⁻²⁷² + . . . + 2^−204592 + . . . + 2^−822850. In the exercises you are asked to explore various data structures for improving the space efficiency of the algorithm.

There is no real meaning to the global state of distributed systems, because global properties cannot be measured. The internal clocks of the processors at each node run independently and cannot be fully synchronized, and precise coordination is impossible because communications channels transfer data at uncertain rates. Nevertheless, there is meaning to the concept of a global snapshot: a consistent recording of the states of all the nodes and channels in a distributed system.

The state of a node is defined to be the values of its internal variables, together with the sequences of messages that have been sent and received along all edges incident with the node. (It is convenient to identify channels with the corresponding edge in the directed graph.) The state of an edge is defined as the sequence of messages sent on the edge but not yet delivered to the receiving node. For a snapshot to be consistent, each message must be in exactly one of these states: sent and in transit in an edge, or already received. It is not required that all the information of a snapshot be gathered at one particular instant, only that the assembly of the information over time be such that consistency is achieved. Algorithms for snapshots are useful because they generalize algorithms for several specific problems, such as detection of termination and deadlock.

The algorithm we present was developed by K. Mani Chandy and Leslie Lamport [22]. Unlike other distributed algorithms in this book, the CL algorithm works only if the channels are FIFO, that is, if the messages are delivered in the order they were sent.

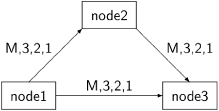
Consider two nodes and the stream of messages sent from node1 to node2:

Suppose that both of these nodes are instructed to take a snapshot. (We leave for now the question of how this occurs.) Presumably we want the snapshot to indicate that node1 has sent fourteen messages (m1, . . . , m14), that node2 has received nine messages (m1,. . . , m9), and that messages m10 through m14 are still on the edge. But node1 has no idea which messages have been received and which are still on the edge, and similarly, node2 can only know which messages it has received, not which messages are on the edge.

To ensure consistency when a snapshot is taken, an additional message called a marker is sent on each edge, in order to place a boundary between messages sent before the snapshot is taken and messages sent after it is taken. Suppose again that both nodes have been instructed to take a snapshot. Let us suppose further that node1 received this command after sending message m11, but before sending message m12. It will send the marker to node2 immediately upon reception of the snapshot command, so the messages on the edge will be as follows:

node1 records its state immediately when the snapshot command is given; its state, therefore, includes messages m1 through m11. node2 also records its state, so the messages received by then—messages m1 through m9—are part of its state. This leaves messages m10 and m11, which have been sent but not received, to be assigned to the state of the edge. Receiving nodes are responsible for recording the state of an edge, which is defined as the set of messages received after it has recorded its state but before it has received the marker.

There is an additional possibility: a node may receive a marker before it is instructed to take a snapshot. In that case, the edge will be considered empty, as all messages received before the marker are considered to be part of the state of the receiving node.

As with the DS algorithm, it is convenient to assume that an environment node is responsible for initiating the algorithm, although the algorithm is very flexible and only requires that every node be reachable from some node that spontaneously decides to record the state. In fact, several nodes could concurrently decide to record the state and the algorithm would still succeed. The environment node will initiate the snapshot by sending a marker on each of its outgoing edges.

for all outgoing edges E
   send(marker, E, myID)

Algorithm 11.6 is the Chandy–Lamport (CL) algorithm for global snapshots. It consists of modifications to the sending and receiving of messages by the underlying algorithm, as well as a process that receives the markers. There is also a process that waits until all markers have been received and then records the state as described below.

To simplify the presentation, we do not store the contents of the messages, only their number within the sequence. Since FIFO channels are assumed these numbers suffice to specify which messages are sent and received. The internal state consists of simply the (number of the) last message sent on each outgoing edge—stored in the variable lastSent during send message, and the (number of the) last message received on each incoming edge—stored in the variable lastReceived during receive message. When the first marker is received, the state of the outgoing edges is recorded in stateAtRecord. All elements of the array are initialized to −1 and this is also used as a flag to indicate that the marker has not been received. (The assignments at p8 and p9 are array assignments; similarly, the test at p7 compares two arrays, although an additional boolean flag would suffice.)

integer array[outgoing] lastSent ← [0, . . . , 0]
integer array[incoming] lastReceived ← [0, . . . , 0]
integer array[outgoing] stateAtRecord ← [−1, . . . , −1]
integer array[incoming] messageAtRecord ← [−1, . . . , −1]
integer array[incoming] messageAtMarker ← [−1, . . . , −1]

p1: send(message, destination, myID)
p2: lastSent[destination] ← message

p3: receive(message, source)
p4: lastReceived[source] ← message

p5: receive(marker, source)
p6: messageAtMarker[source] ← lastReceived[source]
p7: if stateAtRecord = [−1,. . . ,−1]  // Not yet recorded
p8:     stateAtRecord ← lastSent
p9:     messageAtRecord ← lastReceived
p10:    for all outgoing edges E
p11:       send(marker, E, myID)

p12: await markers received on all incoming edges
p13: recordState

For incoming edges, two array variables are needed: messageAtRecord stores the (number of the) last message received on each edge before the state was recorded, and messageAtMarker stores the (number of the) last message received on each edge before the first marker was received.

When the first marker is received, it initiates the recording of the state. For outgoing edges this is easy: the state is simply the last message sent on each edge. Similarly, for the incoming edge upon which the first marker was received, all messages received before the marker are part of the state of the node. For other incoming edges, it is possible that additional messages will be received after the state is recorded, but before the marker is received. The state of the edge is defined as the difference between the last message received before the node recorded its state (in messageAtRecord) and the last message received before the marker was received on this edge (in messageAtMarker).

When marker messages have been received from each incoming edge, the node can record its state, which consists of the following data:

The recorded global state is composed of the state recorded at the individual nodes. An algorithm similar to the DS algorithm can be used to send all the state information back to an environment node.

Let us construct a scenario for an example on the following graph:

Each of the nodes sends three messages 1, 2 and 3 in that order and then a marker M. In the display of the scenario, we have abbreviated the variables: ls for lastSent; lr for lastReceived; sr for stateAtRecord; mr for messageAtRecord; mm for messageAtMarker. Variables that have not changed from their initial values are indicated by a blank cell. The scenario starts by sending all three messages from node1 to node2, where they are received. Then three messages are sent from node1 to node3 and from node2 to node3, but they are not yet received. We display the scenario starting from the first state in this table:

(To save space, the data structures of node3, which are empty, are omitted.) node1, the source node, decides to initiate a snapshot. It sends markers to node2 and node3 (denoted 1M⇒2 and 1M⇒3), and records its own state as having sent three messages on each of its outgoing edges. node2 receives the marker (2⇐1M) and records its state: it has sent three messages and received three messages. We can see that there are no messages on the edge from node1 to node2. Finally, node2 sends a marker to node3 (2M⇒3).

The scenario continues as follows:

(The data structures for node1 and node2, which do not change, are omitted.)

node3 receives the three messages from node2 and updates its lastReceived variable. Then it reads the marker sent by node2 and records its state; again the state shows that the edge from node2 is empty. Finally, node3 receives the three messages from node1 (updating lastReceived as usual), and then receives the marker, recording its state. Since a marker has already been received by this node, messageAtRecord is not updated (p9), but messageAtMarker is updated to reflect the messages received on this edge (p6). The difference between the first components of these two variables indicates that the three messages sent from node1 to node3 are considered to have been on that edge when the snapshot was taken.