A multiprocessor system may have more processors than there are processes in a program. In that case, every process is always running on some processor. In a multitasking system (and similarly in a multiprocessor system in which there are more processes than processors), several processes will have to share the computing resources of a single CPU. A process that “wants to” run, that is, a process that can execute its next statement, is called a ready process. At any one time, there will be one running process and any number of ready processes. (If no processes are ready to run, an idle process will be run.)

A system program called a scheduler is responsible for deciding which of the ready processes should be run, and performing the context switch, replacing a running process with a ready process and changing the state of the running process to ready. Our model of concurrency by interleaving of atomic statements makes no assumptions about the behavior of a scheduler; arbitrary interleaving simply means that the scheduler may perform a context switch at any time, even after executing a single statement of a running process. The reader is referred to textbooks on operating systems [60, 63] for a discussion of the design of schedulers.

Within our model, we do not explicitly mention the concept of a scheduler. However, it is convenient to assume that every process p has associated with it an attribute called its state, denoted p.state. Assignment to this attribute will be used to indicate a change in the state of a process. For example, if p.state = running and q.state = ready, then a context switch between them can be denoted by:

p.state ← ready
q.state ← running

The synchronization constructs that we will define assume that there exists another process state called blocked. When a process is blocked, it is not ready so it is not a candidate for becoming the running process. A blocked process can be unblocked or awakened or released only if an external action changes the process state from blocked to ready. At this point the unblocked process becomes a candidate for execution along with all the current ready processes; with one exception (Section 7.5), an unblocked process will not receive any special treatment that would make it the new running process. Again, within our model we do not describe the implementation of the actions of blocking and unblocking, and simply assume that they happen as defined by the synchronization primitives. Note that the await statement does not block a process; it is merely a shorthand for a process that is always ready, and may be running and checking the truth of a boolean expression.

The following diagram summarizes the possible state changes of a process:

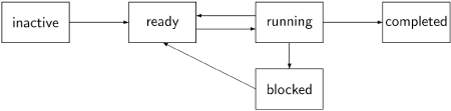
Initially, a process is inactive. At some point it is activated and its state becomes ready. When a concurrent program begins executing, one process is running and the others are ready. While executing, it may encounter a situation that requires the process to cease execution and to become blocked until it is unblocked and returns to the ready state. When a process executes its final statement it becomes completed.

In the BACI concurrency simulator, activation of a process occurs when the coend statement is executed. The activation of concurrent processes in languages such as Ada and Java is somewhat more complicated, because it must take into account the dependency of one process on another.

A semaphore S is a compound data type with two fields, S.V of type non-negative integer, and S.L of type set of processes. We are using the familiar dotted notation of records and structures from programming languages. A semaphore S must be initialized with a value k ≥ 0 for S.V and with the empty set ∅ for the S.L:

semaphore S ← (k, ∅)

There are two atomic operations defined on a semaphore S (where p denotes the process that is executing the statement):^[1]

wait(S)

if S.V > 0
   S.V ← S.V − 1
else
   S.L ← S.L ∪ p
   p.state ← blocked

If the value of the integer component is nonzero, decrement its value (and the process p can continue its execution); otherwise—it is zero—process p is added to the set component and the state of p becomes blocked. We say that p is blocked on the semaphore S.

signal(S)

if S.L = ∅
   S.V ← S.V + 1
else
   let q be an arbitrary element of S.L
   S.L ← S.L − {q}
   q.state ← ready

If S.L is empty, increment the value of the integer component; otherwise—S.L is nonempty—unblock q, an arbitrary element of the set of processes blocked on S.L. The state of process p does not change.

A semaphore whose integer component can take arbitrary non-negative values is called a general semaphore. A semaphore whose integer component takes only the values 0 and 1 is called a binary semaphore. A binary semaphore is initialized with (0, ∅) or (1, ∅). The wait(S) instruction is unchanged, but signal(S) is now defined by:

if S.V = 1
   // undefined
else if S.L = ∅
   S.V ← 1
else // (as above)
   let q be an arbitrary element of S.L
   S.L ← S.L − {q}
   q.state ← ready

A binary semaphore is sometimes called a mutex. This term is used in pthreads and in java.util.concurrent.

Once we have become familiar with semaphores, there will be no need to explicitly write the set of blocked processes S.L.

Using semaphores, the solution of the critical section problem for two processes is trivial (Algorithm 6.1). A process, say p, that wishes to enter its critical section executes a preprotocol that consists only of the wait(S) statement. If S.V = 1 then S.V is decremented and p enters its critical section. When p exits its critical section and executes the postprotocol consisting only of the signal(S) statement, the value of S.V will once more be set to 1.

    loop forever
p1:   non-critical section
p2:   wait(S)
p3:   critical section
p4:   signal(S)

    loop forever
q1:   non-critical section
q2:   wait(S)
q3:   critical section
q4:   signal(S)

If q attempts to enter its critical section by executing wait(S) before p has left, S.V = 0 and q will become blocked on S. S, the value of the semaphore S, will become (0, {q}). When p leaves the critical section and executes signal(S), the “arbitrary” process in the set S.L = {q} will be q, so that process will be unblocked and can continue into its critical section.

The solution is similar to Algorithm 3.6, the second attempt, except that the definition of the semaphore operations as atomic statements prevents interleaving between the test of S.V and the assignment to S.V.

To prove the correctness of the solution, consider the abbreviated algorithm where the non-critical section and critical section statements have been absorbed into the following wait(S) and signal(S) statements, respectively.

    loop forever
p1:   wait(S)
p2:   signal(S)

    loop forever
q1:   wait(S)
q2:   signal(S)

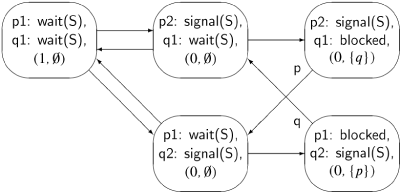
The state diagram for this algorithm is shown in Figure 6.1. Look at the state in the top center, which is reached if initially process p executes its wait statement, successfully entering the critical section. If process q now executes its wait statement, it finds S.V = 0, so the process is added to S.L as shown in the top right state. Since q is blocked, there is no outgoing arrow for q, and we have labeled the only arrow by p to emphasize that fact. Similarly, in the bottom right state, p is blocked and only process q has an outgoing arrow.

Figure 6.1. State diagram for the semaphore solution

A violation of the mutual exclusion requirement would be a state of the form (p2: signal(S), q2: signal(S), . . .). We immediately see that no such state exists, so we conclude that the solution satisfies this requirement. Similarly, there is no deadlock, since there are no states in which both processes are blocked. Finally, the algorithm is free from starvation, since if a process executes its wait statement (thus leaving the non-critical section), it enters either the state with the signal statement (and the critical section) or it enters a state in which it is blocked. But the only way out of a blocked state is into a state in which the blocked process continues with its signal statement.

Let k be the initial value of the integer component of the semaphore, #signal(S) the number of signal(S) statements that have been executed and #wait(S) the number of wait(S) statements that have been executed. (A process that is blocked when executing wait(S) is not considered to have successfully executed the statement.)

Example 6.1. Theorem

A semaphore S satisfies the following invariants:

Equation 6.1. 

Equation 6.2. 

Proof: By definition of a semaphore, k ≥ 0, so 6.1 is initially true, as is 6.2 since #signal(S) and #wait(S) are zero. By assumption, non-semaphore operations cannot change the value of (either component of) a semaphore, so we only need consider the effect of the wait and signal operations. Clearly, 6.1 is invariant under both operations. If either operation changes S.V, the truth of 6.2 is preserved: If a wait operation decrements S.V, then #wait(S) is incremented, and similarly a signal operation that increments S.V also increments #signal(S). If a signal operation unblocks a blocked process, S.V is not changed, but both #signal(S) and #wait(S) increase by one so the righthand side of 6.2 is not changed.

Example 6.2. Theorem

The semaphore solution for the critical section problem is correct: there is mutual exclusion in the access to the critical section, and the program is free from deadlock and starvation.

Proof: Let #CS be the number of processes in their critical sections. We will prove that

Equation 6.3. 

is invariant. By a trivial induction on the structure of the program it follows that

Equation 6.4. 

is invariant. But invariant (6.2) for the initial value k = 1 can be written #wait(S) − #signal(S) = 1 − S.V, so it follows that #CS = 1 − S.V is invariant, and this can be written as #CS + S.V = 1.

Since S.V ≥ 0 by invariant (6.1), simple arithmetic shows that #CS ≤ 1, which proves the mutual exclusion property.

For the algorithm to enter deadlock, both processes must be blocked on the wait statement and S.V = 0. Since neither process is in the critical section, #CS = 0. Therefore #CS + S.V = 0, which contradicts invariant (6.3).

Suppose that some process, say p, is starved. It must be indefinitely blocked on the semaphore so S = (0 , S.L), where p is in the list S.L. By invariant (6.3), #CS = 1 − S.V = 1 − 0 = 1, so the other process q is in the critical section. By progress, q will complete the critical section and execute signal(S). Since there are only two processes in the program, S.L must equal the singleton set {p}, so p will be unblocked and enter its critical section.

Using semaphores, the same algorithm gives a solution for the critical section problem for N processes:

    loop forever
p1:   non-critical section
p2:   wait(S)
p3:   critical section
p4:   signal(S)

The proofs in Theorem 6.2 remain unchanged for N processes as far as mutual exclusion and freedom from deadlock are concerned. Unfortunately, freedeom from starvation does not hold. For the abbreviated algorithm:

    loop forever
p1:   wait(S)
p2:   signal(S)

consider the following scenario for three processes, where the statement numbers for processes q and r correspond to those for p in Algorithm 6.4:

Line 7 is the same as line 3 and the scenario can continue indefinitely in this loop of states. The two processes p and r “conspire” to starve process q.

When there were only two processes, we used the fact that S.L is the singleton set {p} to claim that process p must be unblocked, but with more than two processes this claim no longer holds. Starvation is caused by the fact that, in our definition of the semaphore type, a signal operation may unblock an arbitrary element of S.L. Freedom from starvation does not occur if the definition of the semaphore type is changed so that S.L is a queue not a set. (See Section 6.8 for a comparison of semaphore definitions.)

In the exercises, you are asked to show that if the initial value of S.V is k, then at most k processes can be in the critical section at any time.

The critical section problem is an abstraction of synchronization problems that occur when several processes compete for the same resource. Synchronization problems are also common when processes must coordinate the order of execution of operations of different processes. For example, consider the problem of the concurrent execution of one step of the mergesort algorithm, where an array is divided into two halves, the two halves are sorted concurrently and the results are merged together. Thus, to mergesort the array [5, 1, 10, 7, 4, 3, 12, 8], we divide it into two halves [5, 1, 10, 7] and [4, 3, 12, 8], sort them obtaining [1, 5, 7, 10] and [3, 4, 8, 12], respectively, and then merge the two sorted arrays to obtain [1, 3, 4, 5, 7, 8, 10, 12].

To perform this algorithm concurrently, we will use three processes, two for sorting and one for merging. Clearly, the two sort processes work on totally independent data and need no synchronization, while the merge process must not execute its statements until the two other have completed. Here is a solution using two binary semaphores:

integer array A
binary semaphore S1 ← (0, ∅)
binary semaphore S2 ← (0, ∅)

p1: sort 1st half of A
p2: signal(S1)
p3:

q1: sort 2nd half of A
q2: signal(S2)
q3:

r1: wait(S1)
r2: wait(S2)
r3: merge halves of A

The integer components of the semaphores are initialized to zero, so process merge is initially blocked on S1. Suppose that process sort1 completes before process sort2; then sort1 signals S1 enabling merge to proceed, but it is then blocked on semaphore S2. Only when sort2 completes will merge be unblocked and begin executing its algorithm. If sort2 completes before sort1, it will execute signal(S2), but merge will still be blocked on S1 until sort1 completes.

The producer–consumer problem is an example of an order-of-execution problem. There are two types of processes in this problem:

Producers. A producer process executes a statement produce to create a data element and then sends this element to the consumer processes.

Consumers. Upon receipt of a data element from the producer processes, a consumer process executes a statement consume with the data element as a parameter.

As with the critical section and non-critical section statements, the produce and consume statements are assumed not to affect the additional variables used for synchronization and they can be omitted in abbreviated versions of the algorithms.

Producers and consumers are ubiquitous in computing systems:

When a data element must be sent from one process to another, the communications can be synchronous, that is, communications cannot take place until both the producer and the consumer are ready to do so. Synchronous communication is discussed in detail in Chapter 8.

More common, however, is asynchronous communications in which the communications channel itself has some capacity for storing data elements. This store, which is a queue of data elements, is called a buffer. The producer executes an append operation to place a data element on the tail of the queue, and the consumer executes a take operation to remove a data element from the head of the queue.

The use of a buffer allows processes of similar average speeds to proceed smoothly in spite of differences in transient performance. It is important to understand that a buffer is of no use if the average speeds of the two processes are very different. For example, if your web browser continually produces and sends more data than your communications line can carry, the buffer will always be full and there is no advantage to using one. A buffer can also be used to resolve a clash in the structure of data. For example, when you download a compressed archive (a zip file), the files inside cannot be accessed until the entire archive has been read.

There are two synchronization issues that arise in the producer–consumer problem: first, a consumer cannot take a data element from an empty buffer, and second, since the size of any buffer is finite, a producer cannot append a data element to a full buffer. Obviously, there is no such thing as an infinite buffer, but if the buffer is very large compared to the rate at which data is produced, you might want to avoid the extra overhead required by a finite buffer algorithm and risk an occasional loss of data. Loss of data will occur when the producer tries to append a data element to a full buffer; either the operation will not succeed, in which case that element is lost, or it will overwrite one of the existing elements in the buffer (see Section 13.6).

Infinite Buffers

If there is an infinite buffer, there is only one interaction that must be synchronized: the consumer must not attempt a take operation from an empty buffer. This is an order-of-execution problem like the mergesort algorithm; the difference is that it happens repeatedly within a loop.

Table 6.6. producer–consumer (infinite buffer)

	infinite queue of dataType buffer ← empty queue semaphore notEmpty ← (0, ∅)
producer		consumer
dataType d loop forever p1: d ← produce p2: append(d, buffer) p3: signal(notEmpty)		dataType d loop forever q1: wait(notEmpty) q2: d ← take(buffer) q3: consume(d)

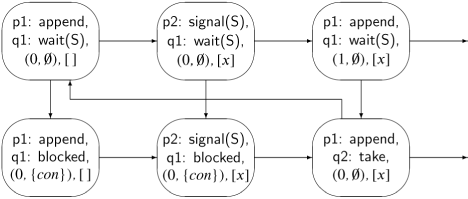
Since the buffer is infinite, it is impossible to construct a finite state diagram for the algorithm. A partial state diagram for the abbreviated algorithm:

Table 6.7. producer–consumer (infinite buffer, abbreviated)

	infinite queue of dataType buffer ← empty queue semaphore notEmpty ← (0, ∅)
producer		consumer
dataType d loop forever p1: append(d, buffer) p2: signal(notEmpty)		dataType d loop forever q1: wait(notEmpty) q2: d ← take(buffer)

is shown in Figure 6.2. In the diagram, the value of the buffer is written with square brackets and a buffer element is denoted by x; the consumer process is denoted by con. The horizontal arrows indicate execution of operations by the producer, while the vertical arrows are for the consumer. Note that the left two states in the lower row have no arrows for the consumer because it is blocked.

Figure 6.2. Partial state diagram for producer–consumer with infinite buffer

Assume now that the two statements of each process form one atomic statement each. (You are asked to remove this restriction in an exercise.) The following invariant holds:

notEmpty.V = #buffer,

where #buffer is the number of elements in buffer. The formula is true initially since there are no elements in the buffer and the value of the integer component of the semaphore is zero. Each execution of the statements of the producer appends an element to the buffer and also increments the value of notEmpty.V. Each execution of the statements of the consumer takes an element from the buffer and also decrements the value of notEmpty.V. From the invariant, it easily follows that the consumer does not remove an element from an empty buffer.

The algorithm is free from deadlock because as long as the producer continues to produce data elements, it will execute signal(notEmpty) operations and unblock the consumer. Since there is only one possible blocked process, the algorithm is also free from starvation.

finite queue of dataType buffer ← empty queue
semaphore notEmpty ← (0, ∅)
semaphore notFull ← (N, ∅)

    dataType d
    loop forever
p1:   d ← produce
p2:   wait(notFull)
p3:   append(d, buffer)
p4:   signal(notEmpty)

    dataType d
    loop forever
q1:   wait(notEmpty)
q2:   d ← take(buffer)
q3:   signal(notFull)
q4:   consume(d)

There are several different definitions of the semaphore type and it is important to be able to distinguish between them. The differences have to do with the specification of liveness properties; they do not affect the safety properties that follow from the semaphore invariants, so the solution we gave for the critical-section problem satisfies the mutual exclusion requirement whatever definition we use.

if S.V > 0
   S.V ← S.V − 1
else
   S.L ← append(S.L, p)
   p.state ← blocked

if S.L = ∅
   S.V ← S.V + 1
else
   q ← head(S.L)
   S.L ← tail (S.L)
   q.state ← ready

await S > 0
S ← S − 1

S ← S + 1

The problem of the dining philosophers is a classical problem in the field of concurrent programming. It offers an entertaining vehicle for comparing various formalisms for writing and proving concurrent programs, because it is sufficiently simple to be tractable yet subtle enough to be challenging.

The problem is set in a secluded community of five philosophers who engage in only two activities—thinking and eating:

    loop forever
p1:   think
p2:   preprotocol
p3:   eat
p4:   postprotocol

Meals are taken communally at a table set with five plates and five forks (Figure 6.3). In the center of the table is a bowl of spaghetti that is endlessly replenished. Unfortunately, the spaghetti is hopelessly tangled and a philosopher needs two forks in order to eat.^[2] Each philosopher may pick up the forks on his left and right, but only one at a time. The problem is to design pre- and postprotocols to ensure that a philosopher only eats if she has two forks. The solution should also satisfy the correctness properties that we described in the chapter on mutual exclusion.

Figure 6.3. The dining philosophers

The correctness properties are:

Here is a first attempt at a solution, where we assume that each philosopher is initialized with its index i, and that addition is implicitly modulo 5.

    loop forever
p1:   think
p2:   wait(fork[i])
p3:   wait(fork[i+1])
p4:   eat
p5:   signal(fork[i])
p6:   signal(fork[i+1])

Each fork is modeled as a semaphore: wait corresponds to taking a fork and signal corresponds to putting down a fork. Clearly, a philosopher holds both forks before eating.

Unfortunately, this solution deadlocks under an interleaving that has all philosophers pick up their left forks—execute wait(fork[i])—before any of them tries to pick up a right fork. Now they are all waiting on their right forks, but no process will ever execute a signal operation.

One way of ensuring liveness in a solution to the dining philosophers problem is to limit the number of philosophers entering the dining room to four:

semaphore array[0..4] fork ← [1,1,1,1,1]
semaphore room ← 4

    loop forever
p1:   think
p2:   wait(room)
p3:   wait(fork[i])
p4:   wait(fork[i+1])
p5:   eat
p6:   signal(fork[i])
p7:   signal(fork[i+1])
p8:   signal(room)

The addition of the semaphore room obviously does not affect the correctness of the safety properties we have proved.

Another solution that is free from starvation is an asymmetric algorithm, which has the first four philosophers execute the original solution, but the fifth philosopher waits first for the right fork and then for the left fork:

    loop forever
p1:   think
p2:   wait(fork[0])
p3:   wait(fork[4])
p4:   eat
p5:   signal(fork[0])
p6:   signal(fork[4])

Again it is obvious that the correctness properties on eating are satisfied. Proofs of freedom from deadlock and freedom from starvation are similar to those of the previous algorithm and are left as an exercise.

A solution to the dining philosophers problem by Lehmann and Rabin uses random numbers. Each philosopher “flips a coin” to decide whether to take her left or right fork first. It can be shown that with probability one no philosopher starves [48, Section 11.4].

In this section we present Hans W. Barz’s simulation of a general semaphore by a pair of binary semaphores and an integer variable [6]. (See [67] for a survey of the attempts to solve this problem.) The simulation will be presented within the

binary semaphore S ← 1
binary semaphore gate ← 1
integer count ← k

    loop forever
      non-critical section

p1:   wait(gate)                  // Simulated wait
p2:   wait(S)
p3:   count ← count − 1
p4:   if count > 0 then
p5:      signal(gate)
p6:   signal(S)

      critical section

p7:   wait(S)                     // Simulated signal
p8:   count ← count + 1
p9:   if count = 1 then
p10:     signal(gate)
p11:  signal(S)

context of a solution of the critical section problem that allows k > 0 processes simultaneously in the critical section (Algorithm 6.13).

k is the initial value of the general semaphore, statements p1..6 simulate the wait statement, and statements p7..11 simulate the signal statement. The binary semaphore gate is used to block and unblock processes, while the variable count holds the value of the integer component of the simulated general semaphore. The second binary semaphore S is used to ensure mutual exclusion when accessing count. Since we will be proving only the safety property that mutual exclusion holds, it will be convenient to consider the binary semaphores as busy-wait semaphores, and to write the value of the integer component of the semaphore gate as gate, rather than gate.V.

It is clear from the structure of the algorithm that S is a binary semaphore; it is less clear that gate is one. Therefore, we will not assume anything about the value of gate other than that it is an integer and prove (Lemma 6.5(6), below) that it only takes on the values 0 and 1.

Let us start with an informal description of the algorithm. Since gate is initialized to 1, the first process attempting to execute a simulated wait statement will succeed in passing p1: wait(gate), but additional processes will block. The first process and each subsequent process, up to a total of k − 1, will execute p5: signal(gate), releasing additional processes to successfully complete p1: wait(gate). The if statement at p4 prevents the k th process from executing p5: signal(gate), so further processes will be blocked at p1: wait(gate).

When count = 0, a single simulated signal operation will increment count and execute p11: signal(gate), unblocking one of the processes blocked at p1: wait(gate); this process will promptly decrement count back to zero. A sequence of simulated signal operations, however, will cause count to have a positive value, although the value of gate remains 1 since it is only signaled once. Once count has a positive value, one or more processes can now successfully execute the simulated wait.

An inductive proof of the algorithm is quite complex, but it is worth studying because so many incorrect algorithms have been proposed for this problem.

In the proof, we will reduce the number of steps in the induction to three. The binary semaphore S prevents the statements p2..6 from interleaving with the statements p7..11. p1 can interleave with statements p2..6 or p7..11, but cannot affect their execution, so the effect is the same as if all the statements p2..6 or p7..11 were executed before p1.^[3]

We will use the notation entering for p2..6 and inCS for p7. We also denote by #entering, respectively #inCS, the number of processes for which entering, respectively inCS, is true.

The implementation of Barz’s algorithm in Promela is discussed in Section 6.15.

There are solutions to the critical-section problem using weak semaphores that are free of starvation. We give without proof a solution developed by Jan T. Udding [68]. Algorithm 6.14 is similar to the fast algorithms described in Section 5.4, with two gates that must be passed in order to enter the critical section.

semaphore gate1 ← 1, gate2 ← 0
integer numGate1 ← 0, numGate2 ← 0

    loop forever
      non-critical section

p1:   wait(gate1)
p2:   numGate1 ← numGate1 + 1
p3:   signal(gate1)

p4:   wait(gate1)              // First gate
p5:   numGate2 ← numGate2 + 1
p6:   if numGate1 > 0
p7:      signal(gate1)
p8:   else signal(gate2)

p9:   wait(gate2)              // Second gate
p10:  numGate2 ← numGate2 − 1

      critical section
p11:  if numGate2 > 0
p12:     signal(gate2)
p13:  else signal(gate1)

The two semaphores constitute a split binary semaphore satisfying 0 ≤ gate1 + gate2 ≤ 1, and the integer variables count the number of processes about to enter or trying to enter each gate.

The semaphore gate1 is reused to provided mutual exclusion during the initial increment of numGate1. In our model, where each line is an atomic operation, this protection is not needed, but freedom from starvation depends on it so we have included it.

The idea behind the algorithm is that processes successfully pass through a gate (complete the wait operation) as a group, without interleaving wait operations from the other processes. Thus a process p passing through gate2 into the critical section may quickly rejoin the group of processes in front of gate1, but all of the colleagues from its group will enter the critical section before p passes the first gate again. This ensures that the algorithm is free from starvation.

The attempted solution still suffers from the possibility of starvation, as shown by the following outline of a scenario:

Two processes are denoted p and q with appropriate line numbers; the third process r is omitted because it remains blocked at r1: wait(g1) throughout the scenario. Variable names have been shortened: gate to g and numGate to nGate.

The scenario starts with processes p and q at gates p4 and q4, respectively, while the third process r has yet to pass the initial wait operation at r1. The key line in the scenario is line 7, where q unblocks his old colleague p waiting again at p1 instead of r who has been waiting at r1 for quite a long time.

By adding an additional semaphore, we can ensure that at most one process is at the second gate at any one time. The semaphore onlyOne is initialized to 1, a wait(onlyOne) operation is added before p4 and a signal(onlyOne) operation is added before p9. This ensures that at most one process will be blocked at gate1.

Types semaphore and binarysem with the operations wait and signal are defined in both the C and Pascal dialects of BACI. The implementation is of weak semaphores: when a signal statement is executed, the list of processes blocked on this semaphore is searched starting from a random position in the list.

The Ada language does not include a semaphore type, but it is easily implemented using protected types:^[4]

 1 protected type Semaphore(Initial : Natural) is
 2   entry Wait;
 3   procedure Signal;
 4 private
 5   Count: Natural := Initial;
 6 end Semaphore;
 7
 8 protected body Semaphore is
 9   entry Wait when Count > 0 is
10   begin
11     Count := Count − 1;
12   end Wait;
13
14   procedure Signal is
15   begin
16     Count := Count + 1;
17     end Signal;
18 end Semaphore;

The private variable Count is used to store the integer component of the semaphore. The queue of the entry Wait is the queue of the processes blocked on the semaphore, and its barrier when Count > 0 ensures that the wait operation can be executed only if the value of Count is positive. Since entry queues in Ada are defined to be FIFO queues, this code implements a strong semaphore.

To use this semaphore, declare a variable with a value for the discriminant Initial and then invoke the protected operations:

S: Semaphore(1);
. . .
S.wait;
−− critical section
S.signal;

The Semaphore class is defined within the package java.util.concurrent. The terminology is slightly different from the one we have been using. The integer component of an object of class Semaphore is called the number of permits of the object, and unusually, it can be initialized to be negative. The wait and signal operations are called acquire and release, respectively. The acquire operation can throw the exception InterruptedException which must be caught or thrown.

Here is a Java program for the counting algorithm with a semaphore added to ensure that the two assignment statements are executed with no interleaving.

 1 import java.util . concurrent. Semaphore;
 2 class CountSem extends Thread {
 3   static volatile int n = 0;
 4   static Semaphore s = new Semaphore(1);
 5
 6   public void run() {
 7     int temp;
 8     for (int i = 0; i < 10; i ++) {
 9       try {
10         s. acquire ();
11       }
12       catch (InterruptedException e) {}
13       temp = n;
14       n = temp + 1;
15       s. release ();
16     }
17   }
18
19   public static void main(String[] args) {
20       // (as before)
21   }
22 }

The constructor for class Semaphore includes an extra boolean parameter used to specify if the semaphore is fair or not. A fair semaphore is what we have called a strong semaphore, but an unfair semaphore is more like a busy-wait semaphore than a weak semaphore, because the release method simply unblocks a process but does not acquire the lock associated with the semaphore. (See Section 7.11 for more details on synchronization in Java.)

In Promela it is easy to implement a busy-wait semaphore:

#define wait(s) atomic {s > 0; s−− }
#define signal(s) s++

Statements within atomic are executed without interleaving, except that if a statement blocks, statements from other processes will be executed. In wait(s), either the two instructions will be executed as one atomic statement, or the process will block because s = 0; when it can finally be executed because s > 0, the two statements will be executed atomically.

To implement a weak semaphore, we must explicitly store S.L, the set of blocked processes. We declare a semaphore type definition containing an integer field for the V component of the semaphore and a boolean array field for the L component with an element for each of NPROCS processes:

typedef Semaphore {
   byte count;
   bool blocked[NPROCS];
};

Inline definitions are used for the semaphore operations, beginning with an operation to initialize the semaphore:

inline initSem(S, n) { S.count = n }

If the count is positive, the wait operation decrements the count; otherwise, the process is blocked waiting for this variable to become false:

inline wait(S) {
    atomic {
      if
      :: S.count >= 1 −> S.count−−
      :: else −>
           S.blocked[ _pid−1] = true;
           ! S.blocked[ _pid−1]
      fi
    }
}

The semaphore is initialized in the init process whose _pid is zero, so the other processes have _pids starting from one.

The signal operation nondeterministically sets one of the blocked processes to be unblocked. If there are no blocked processes, the count is incremented. The following code assumes that there are three processes:

inline signal (S) {
    atomic {
      if
      :: S.blocked[0] −> S.blocked[0] = false
      :: S.blocked[1] −> S.blocked[1] = false
      :: S.blocked[2] −> S.blocked[2] = false
      :: else −> S.count++
      fi
    }
}

The code for an arbitrary number of processes is more complicated:

inline signal (S) {
    atomic {
      S.i = 0;
      S.choice = 255;
      do
      :: (S.i == NPROCS) −> break
      :: (S.i < NPROCS) && !S.blocked[S.i] −> S.i++
      :: else −>
          if
          :: (S.choice == 255) −> S.choice = S.i
          :: (S.choice != 255) −> S.choice = S.i
          :: (S.choice != 255) −>
          fi;
          S.i ++
      od;
      if
      :: S.choice == 255 −> S.count++
      :: else −> S.blocked[S.choice] = false
      fi
    }
}

Two additional variables are added to the typedef: i to loop through the array of blocked processes, and choice to record the choice of a process to unblock, where 255 indicates that a process has yet to be chosen. If some process is blocked—indicated by S.blocked[ S.i ] being true—we nondeterministically choose either to select it by assigning its index to S.choice or to ignore it.

The implementation of strong semaphores using channels is left as an exercise. We also present an implementation of weak semaphores using channels, that is not restricted to a fixed number of processes.

 1 #define NPROCS 3
 2 #define K     2
 3 byte gate = 1;
 4 int count = K;
 5 byte critical = 0;
 6 active [ NPROCS] proctype P () {
 7   do ::
 8     atomic { gate > 0; gate−−; }
 9     d_step {
10       count−−;
11       if
12       :: count > 0 −> gate++
13       :: else
14       fi
15     }
16     critical ++;
17     assert (critical <= 1);
18     critical −−;
19     d_step {
20       count++;
21       if
22       :: count == 1 −> gate++
23       :: else
24       fi
25     }
26   od
27 }

Exercises

1.	Consider the following algorithm: Table 6.15. Semaphore algorithm A semaphore S ← 1, T ← 0 p q p1: wait(S) p2: write("p") p3: signal(T) q1: wait(T) q2: write("q") q3: signal(S) What are the possible outputs of this algorithm? What are the possible outputs if we erase the statement wait(S)? What are the possible outputs if we erase the statement wait(T)?
2.	What are the possible outputs of the following algorithm? Table 6.16. Semaphore algorithm B semaphore S1 ← 0, S2 ← 0 p q r p1: write("p") p2: signal(S1) p3: signal(S2) q1: wait(S1) q2: write("q") q3: r1: wait(S2) r2: write("r") r3:
3.	What are the possible outputs of the following algorithm? Table 6.17. Semaphore algorithm with a loop   semaphore S ← 1 boolean B ← false p   q p1: wait(S) p2: B ← true p3: signal(S) p4: q1: wait(S) q2: while not B q3: write("*") q4: signal(S)
4.	Show that if the initial value of S.V in Algorithm 6.3 is k, at most k processes can be in the critical section at any time.
5.	The following algorithm attempts to use binary semaphores to solve the critical section problem with at most k out of N processes in the critical section: Table 6.18. Critical section problem (k out of N processes)   binary semaphore S ← 1, delay ← 0 integer count ← k integer m loop forever p1: non-critical section p2: wait(S) p3: count ← count − 1 p4: m ← count p5: signal(S) p6: if m ≤ −1 p7: wait(delay) p8: critical section p9: wait(S) p10: count ← count + 1 p11: if count ≤ 0 p12: signal(delay) p13: signal(S) For N = 4 and k = 2, construct a scenario in which delay = 2, contrary to the definition of a binary semaphore. Show this also for N = 3 and k = 2.
6.	Modify Algorithm 6.5 to use a single general semaphore.
7.	Prove the correctness of Algorithm 6.7 without the assumption of atomicity.
8.	Develop an abbreviated version of Algorithm 6.8. Assumimg atomicity of the statements of each process, show that notFull.V = N − #Buffer is invariant. What correctness property can you conclude from this invariant?
9.	A bounded buffer is frequently implemented using a circular buffer, which is an array that is indexed modulo its length: One variable, in, contains the index of the first empty space and another, out, the index of the first full space. If in > out, there is data in buffer[out..in-1]; if in < out, there is data in buffer[out..N] and buffer[0..in-1]; if in = out, the buffer is empty. Prove the correctness of the following algorithm for the producer–consumer problem with a circular buffer: Table 6.19. producer–consumer (circular buffer)   dataType array[0..N] buffer integer in, out ← 0 semaphore notEmpty ← (0, ∅) semaphore notFull ← (N, ∅) producer   consumer dataType d loop forever p1: d ← produce p2: wait(notFull) p3: buffer[in] ← d p4: in ← (in+1) modulo N p5: signal(notEmpty) dataType d loop forever q1: wait(notEmpty) q2: d ← buffer[out] q3: out ← (out+1) modulo N q4: signal(notFull) q5: consume(d)
10.	Prove the correctness of the asymmetric solution to the dining philosophers problem (Algorithm 6.12).
11.	A partial scenario for starvation in Udding’s algorithm was given on page 131; complete the scenario.
12.	Prove or disprove the correctness of Algorithm 6.20 for implementing a general semaphore by binary semaphores.
13.	Implement a strong semaphore in Promela. Table 6.20. Simulating general semaphores   binary semaphore S ← 1, gate ← 0 integer count ← 0 wait   p1: wait(S) p2: count ← count − 1 p3: if count < 0 p4: signal(S) p5: wait(gate) p6: else signal(S) signal   p7: wait(S) p8: count ← count + 1 p9: if count ≤ 0 p10: signal(gate) p11: signal(S)
14.	Here is a version of the implementation of the signal operation of a weak semaphore in Promela that does not use the variable choice. Is the program correct? inline signal (S) { atomic { S.i = 0; do :: S.i == NPROCS −> break :: (S.i < NPROCS) && S.blocked[S.i] −> break :: (S.i < NPROCS) && S.blocked[S.i] −> S.i++ :: (S.i < NPROCS) && !S.blocked[S.i] −> S.i++ od; if :: S.i == NPROCS −> S.count++ :: else −> S.blocked[S.i] = false fi } }
15.	Weak semaphores can be implemented in Promela by storing the blocked processes in a channel: chan ch = [NPROCS] of { pid }; Explain the following implementations of the wait and signal operations:[5] inline wait(S) { atomic { if :: S.count >= 1 −> S.count−−; :: else −> S.ch ! _pid; !(S.ch ?? [eval(_pid)]) fi } } inline signal (S) { atomic { S.i = len(S.ch); if :: S.i == 0 −> S.count++ :: else −> do :: S.i == 1 −> S.ch ? _; break :: else −> S.i −−; S.ch ? S.temp; if :: break :: S.ch ! S.temp fi od fi } }
16.	[2, Section 4.4][6] Algorithm 6.21 is a solution of the problem of the readers and writers using semaphores. SignalProcess is a subprogram that is executed following each of the start and end operations. Prove that entry, readerSem and writerSem form a split binary semaphore, that is, prove that 0 ≤ entry + readerSem + writerSem ≤ 1 . Prove the correctness of the algorithm by showing the invariance of: (writers > 0) → (writers = 1) ∧ (readers = 0). The subprogram SignalProcess is uniform for all the operations. Simplify the algorithm by writing separate code for each of the operations. Show that readers are given precedence over writers. Modify the algorithm to give writers precedence over readers. Modify the algorithm to give alternate precedence to readers and writers. Table 6.21. Readers and writers with semaphores   semaphore readerSem ← 0, writerSem ← 0 integer delayedReaders ← 0, delayedWriters ← 0 semaphore entry ← 1 integer readers ← 0, writers ← 0 SignalProcess   if writers = 0 or delayedReaders > 0 delayedReaders ← delayedReaders − 1 signal(readerSem) else if readers = 0 and writers = 0 and delayedWriters > 0 delayedWriters ← delayedWriters − 1 signal(writerSem) else signal(entry) StartRead   p1: wait(entry) p2: if writers > 0 p3: delayedReaders ← delayedReaders + 1 p4: signal(entry) p5: wait(readerSem) p6: readers ← readers + 1 p7: SignalProcess EndRead   p8: wait(entry) p9: readers ← readers − 1 p10: SignalProcess StartWrite   p11: wait(entry) p12: if writers > 0 or readers > 0 p13: delayedWriters ← delayedWriters + 1 p14: signal(entry) p15: wait(writerSem) p16: writers ← writers + 1 p17: SignalProcess EndWrite   p18: wait(entry) p19: writers ← writers − 1 p20: SignalProcess