One of the primary motivations for building distributed systems is to improve reliability by replicating a computation in several independent processors. There are two properties that we can hope to achieve in a reliable system: a system is fail-safe if one or more failures do not cause damage to the system or to its users; a system is fault-tolerant if it continues to fulfil its requirements even if there are one or more failures. A distributed system is not automatically fail-safe or fault-tolerant. The RA algorithm for distributed mutual exclusion requires the cooperation of all the processes and will deadlock if one of them fails. The following diagram shows the general architecture of a reliable system:

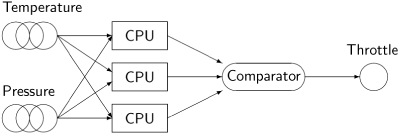
Input sensors are replicated, as are the CPUs performing the computation. The outputs are compared and an algorithm such as majority voting is used to decide what command to send to control the system.

The simplicity of the diagram masks the complexity of the difficulties that must be overcome in designing a reliable system:

The design of such systems is beyond the scope of this book. Here, we will focus on the specific problem of achieving consensus in a distributed system; each node chooses an initial value and it is required that all the nodes in the system decide on one of those values. If there are no faults in the system, there is a trivial algorithm: each node sends its choice to every other node and then an algorithm such as majority voting is performed. Since all nodes have the same data and execute the same algorithm, they all decide upon the same value and consensus is achieved.

We will consider two types of faults:crash failures in which a node simply stops sending messages, and byzantine failures in which a faulty node may send arbitrary messages. The name is taken from the classic algorithm for consensus by Leslie Lamport, Robert Shostak and Marshall Pease called the Byzantine Generals algorithm [42]. After presenting this algorithm, we show a simple flooding algorithm that achieves consensus in the presence of crash failures. We conclude with another algorithm for consensus under byzantine failure developed by Piotr Berman and Juan Garay [11]. This algorithm, called the King algorithm, is much more efficient than the Byzantine Generals algorithm in terms of the number of messages exchanged.

We will prove the correctness of the algorithms for the minimum number of nodes for which the algorithms work; the full proofs are inductive generalizations of the proofs we give and can be found in the original articles and in textbooks [4, 48].

The problem of consensus was originally stated in a rather graphic setting, which has become so entrenched in the literature that we will continue to use it:

Historical note: The Byzantine Empire existed from the year 323 until it was finally destroyed by the Ottoman Turks in 1453. Its capital city Constantinople (now Istanbul) was named after Constantine, the founder of the empire. Its history has given rise to the word byzantine meaning devious and treacherous political maneuvering, though they were probably no worse than any comparable political entity. To maintain the verisimilitude of the story, I will call the nodes of the system by real names of Byzantine emperors.

In terms of distributed systems, the generals model nodes and the messengers model communications channels. While the generals may fail, we assume that the messengers are perfectly reliable. We will model two types of node failures:

Crash failures. A traitor (failure node) simply stops sending messages at any arbitrary point during the execution of the algorithm.

Byzantine failures. A traitor can send arbitrary messages, not just the messages required by the algorithm.

In the case of crash failures, we assume that we know that the node has crashed; for example, there might be a timeout value such that the receiving node knows that any message will arrive within that amount of time. If we have no way to decide if a node has crashed or if a message is merely delayed, the consensus problem is not solvable [48, Chapter 17]. Byzantine failures are more difficult to handle; since it is sufficient that there exist one scenario for the algorithm to be incorrect, we must take into account a “malicious” traitor who designs exactly the set of messages that will break the algorithm.

The requirement that the consensus be “almost” the same as the majority vote ensures that the algorithm will be applicable and that a trivial solution is not given. A trivial solution, for example, is an algorithm stating that all loyal generals decide to attack, but this does not model a system that actually computes a value. Suppose that we have 10 generals of whom 2 are traitors. If the initial choices of the loyal generals are 6 to attack and 2 to retreat, the traitors could cause some generals to think that the choices were split 8–2 and others to think 6–4, but the majority vote is to attack in any case and the algorithm must also ensure that this decision is reached. If, on the other hand, the initial choices were 4–4 or 5–3, it is possible for the traitors to affect the final outcome, as long as there is consensus. This is meaningful, for if four non-faulty computers say to open the throttle and four say to close the throttle, then it probably doesn’t make a difference, as long as they all choose the same command.

The algorithms are intended to be executed concurrently with the underlying computation whenever there is a need to reach consensus concerning the value of an item of data. The set of messages used is disjoint from the set used by the underlying computation. The algorithms are synchronous in the sense that each node sends out a set of messages and then receives replies to those messages. Since different types of messages are not received concurrently, we need not write a specific message type; the send statement includes only the destination node ID followed by the data sent, and the receive statement includes only variables to store the data that is received.

Let us start with the obvious algorithm:

planType finalPlan
planType array[generals] plan

p1:  plan[myID] ← chooseAttackOrRetreat
p2:  for all other generals G
p3:     send(G, myID, plan[myID])
p4:  for all other generals G
p5:     receive(G, plan[G])
p6:  finalPlan ← majority(plan)

The values of planType are A for attack and R for retreat. Each general chooses a plan, sends its plan to the other generals and receives their plans. The final plan is the majority vote among all plans, both the general’s own plan and the plans received from the others.

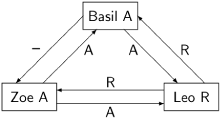
Suppose now that there are three generals, two of whom—Zoe and Leo—are loyal, and the third—Basil—is a traitor. Basil and Zoe choose to attack, while Leo chooses to retreat. The following diagram shows the exchange of messages according to the algorithm, where Basil has crashed after sending a message to Leo that he has chosen to attack, but before sending a similar message to Zoe:

The following tables show the content of the array plan at each of the loyal nodes, as well as the result of the majority vote:

By a majority vote of 2–1, Leo chooses A. Zoe chooses R, because ties are (arbitrarily) broken in favor of R. We see that if a general crashes, it can cause the remaining loyal generals to fail to come to a consensus. It should be clear that this scenario can be extended to an arbitrary number of generals. Even if just a few generals crash, they can cause the remaining generals to fail to achieve consensus if the vote is very close.

The problem with the one-round algorithm is that we are not using the fact that certain generals are loyal. Leo should somehow be able to attribute more weight to the plan received from the loyal general Zoe than from the traitor Basil. In a distributed system an individual node cannot know the identities of the traitors directly; rather, it must ensure that the plan of the traitors cannot cause the loyal generals to fail to reach consensus. The Byzantine Generals algorithm achieves this by using extra rounds of sending messages: a first round in which each general sends its own plan, and subsequent rounds in which each general sends what it received from other generals about their plans. By definition, loyal generals always relay exactly what they received, so that if there are enough loyal generals, they can overcome the attempts of the traitors to prevent them from reaching a consensus.

Algorithm 12.2 is the two-round Byzantine Generals algorithm. The first round is the same as before; at its conclusion, the array plan holds the plans of each of the generals. In the second round, these plans are then sent to the other generals. Obviously, a general doesn’t have to send her own plan to herself, nor does she have to send back to another general what he reported about himself. Therefore, each round reduces by one the number of messages that a general needs to send.

The line p8: send(G', myID, G, plan[G]) means: send to general G' that I (myID) received the plan stored in plan[G] from general G. When such a message is received, it is stored in reportedPlans, where the value of the array element report-edplan[G, G'] is the plan that G reported receiving from G'.

planType finalPlan
planType array[generals]
plan planType array[generals, generals] reportedPlan
planType array[generals] majorityPlan

p1:  plan[myID] ← chooseAttackOrRetreat

p2:  for all other generals G                   // First round
p3:     send(G, myID, plan[myID])
p4:  for all other generals G
p5:     receive(G, plan[G])

p6:  for all other generals G                   // Second round
p7:     for all other generals G' except G
p8:        send(G', myID, G, plan[G])
p9:  for all other generals G
p10:    for all other generals G' except G
p11:       receive(G, G', reportedPlan[G, G'])

p12: for all other generals G                   // First vote
p13:    majorityPlan[G] ← majority(plan[G] ∪ reportedPlan[*, G])

p14: majorityPlan[myID] ← plan[myID]           // Second vote
p15: finalPlan ← majority(majorityPlan)

Voting is done in a two-stage procedure. For each other general G, a majority vote is taken of the plan received directly from G—the value of plan[G]—together with the reported plans for G received from the other generals—denoted in the algorithm by reportedPlan[*,G]. This is taken as the “real” intention of G and is stored in majorityplan[G]. The final decision is obtained from a second majority vote of the values stored in majorityPlan, which also contains plan[myID].

Don’t worry if the algorithm seems confusing at this point! The concept will become clearer as we work through some examples.

Let us first examine the Byzantine Generals algorithm in the case of crash failures with three generals, one of whom is a traitor. Here are the data structures of the two loyal generals for the same scenario as in Section 12.3, where Basil crashes after sending the (first-round) message to Leo, but before sending it to Zoe:

The second column shows the general’s own choice of plan and the plans received directly from the other generals, while the third and fourth columns show the plans reported in the second round. The last column shows the majority vote for each general. Obviously, a loyal general’s own plan is correct; it is not sent and no report is received. For the other loyal general (Leo for Zoe and Zoe for Leo), the correct plan is received on the first round. Basil, having crashed during the first round, does not send second-round messages.

Basil sends a message to one of the loyal generals, Leo, and Leo relays this information to Zoe in the second round (denoted by A). If a general sends even one message before crashing, all the loyal generals receive the same report of this plan, and the majority vote will be the same for each of them.

Let us check one more scenario, in which the traitor sends out all of its first-round messages and one of its second-round messages before crashing. Basil has sent to Leo a message reporting that Zoe’s plan is to attack, but crashes before sending the report on Leo to Zoe. There is only one missing message:

Again, both loyal generals have consistent data structures and come to the same decision about the final plan.

To prove the correctness of the Byzantine Generals algorithm, we will use knowledge trees.^[1] A knowledge tree stores the data that is known about the general listed at its root. Therefore, the tree is not a data structure that exists locally at any node, but rather a virtual global data structure obtained by integrating the local data structures. The following diagram shows the knowledge tree about Basil, assuming that Basil has chosen A and that all messages, both from Basil and from the other nodes, have been sent and received:

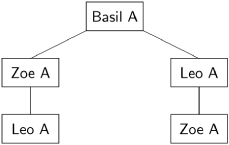
The root of the tree shows that Basil has chosen to attack. The first level below the root shows the results of the first round of messages: Basil sends his plan to both Leo and Zoe. The second level below the root shows the results of the second round of messages: Zoe sends to Leo that Basil’s plan is to attack and Leo sends to Zoe that Basil’s plan is to attack. Both Zoe and Leo receive two messages about Basil, and both messages are the same.

We can use knowledge trees to prove the correctness of Algorithm 12.2 under crash failures when there are three generals, one of whom is a traitor. We show that in any scenario, both Leo and Zoe come to the same conclusion about Basil’s plan.

If Basil sends no messages, both Zoe and Leo know nothing about Basil’s plan, but they correctly send their own plans to each other. Together with their own plans, the two generals have the same set of plans and reach the same decision.

If Basil sends exactly one first-round message before crashing, then since both Zoe and Leo are loyal, the one who receives it (say, Leo) will report the message to the other. Exactly one branch of the tree will be constructed, as shown in the following diagram where we have represented an arbitrary plan chosen by Basil as X:

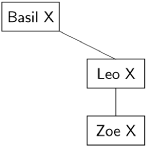
Both Zoe and Leo have exactly one message each about Basil’s plan and will vote the same way.

If Basil sends two first-round messages, the result is the first tree in this section with A replaced by the arbitrary X. Both Zoe and Leo have received the same two messages about Basil’s plan and come to the same decision.

We also have to consider the possibility that a crash of Basil before a second-round message can cause Leo to make an inconsistent decision about Zoe, or vice versa. Here is the knowledge tree about Leo that results if Basil crashes before sending the second-round message to Zoe:

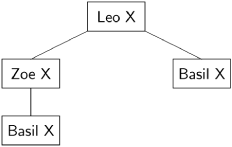
Leo of course knows his own plan X and Zoe knows the same plan having received it during the first round directly from the loyal Leo. Therefore, both Leo and Zoe come to the same decision about Leo’s choice.

The two-round Byzantine Generals algorithm is much more complicated than it need be for a system that suffers only from crash failures. (A simpler algorithm is given in Section 12.9.) It is only when we consider Byzantine failures that the cleverness of the algorithm becomes apparent. Recall that a byzantine failure is one in which a node can send any message that it pleases, and that an algorithm is incorrect if there is even one set of malicious messages that causes it to fail. In the context of the story of the Byzantine Generals, a traitor is allowed to send an attack or retreat message, regardless of its internal state. In fact, we will not even show a choice of an initial plan for a traitor, because that plan can be totally ignored in deciding which messages are sent.

Here are the messages of the first round of the example from the previous section, where instead of crashing the traitor Basil sends an R message to Zoe:

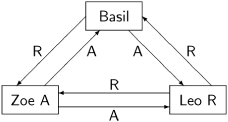
The data structures are as follows and the two loyal generals will make inconsistent final decisions:

We are not surprised, because the one-round algorithm was not correct even in the presence of crash failures.

Consider now the two-round algorithm. In the first round, Basil sends an A message to both Zoe and Leo; in the second round, he correctly reports to Zoe that Leo’s plan is R, but erroneously reports to Leo that Zoe’s plan is R. The following data structure results:

Basil’s byzantine failure has caused Leo to make an erroneous decision about Zoe’s plan (the one-one tie is broken in favor of retreat). The two loyal generals reach inconsistent final decisions, so we conclude that the algorithm is incorrect for three generals of whom one is a traitor.

Let us look at the failure using the knowledge tree about Zoe:

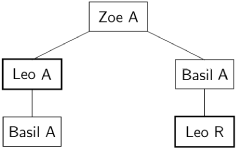
Zoe chose A and sent A messages to Leo and Basil. While the loyal Leo reported Zoe’s choice correctly to Basil, the traitor Basil falsely reported to Leo that Zoe sent him R. Leo has two conflicting reports about Zoe’s plan (thick frames), leading to the wrong decision.

The Byzantine Generals algorithm for consensus is correct if there are three loyal generals and one traitor. When the first votes are taken to decide what each general has chosen, there will be two loyal reports against one report from the traitor, so the loyal generals will agree. We will show a scenario for the algorithm and then use knowledge trees to prove its correctness.

Our fourth general will be named John and we will change the traitor to Zoe. Basil and John choose A while Leo chooses R. Here is a partial data structure of the loyal general Basil; it shows only messages received from the loyal generals, not those from the traitor Zoe:

Basil receives the correct plan of loyal general John, both directly from John himself as well as indirectly from Leo (bold); the report from the traitor Zoe can at worst make the vote 2–1 instead of 3–0, but the result is always correct. Similarly, Basil has two correct reports of the plan of Leo.

Basil now has three correct votes—his own and the ones from John and Leo—as do the other two loyal generals. But it is premature to conclude that they come to a consensus in the final vote, because Zoe could send messages convincing some of them that her plan is A and others that it is R. It remains to show that the three loyal generals come to a consensus about the plan of Zoe.

Let us continue our example and suppose that Zoe sends first-round messages of R to Basil and Leo and A to John; these are relayed correctly in the second round by the loyal generals. Basil’s data structure now becomes:

Clearly, Zoe can send arbitrary messages to the loyal generals, but during the second round these messages are accurately reported by all the loyal generals (bold), leading them to the same majority vote about Zoe’s plan. In the example, the final decision taken by all the loyal generals will be a 2–1 vote in favor of R for Zoe’s plan.

Thus the traitor cannot cause the loyal generals to fail to come to a consensus; at worst, their decision may be slightly influenced. For example, if Zoe had sent attack instead of retreat to Basil, it can be shown that the final decision would have been to attack (exercise). If the loyal generals initially choose the same plan, the final decision would be this plan, regardless of the actions of the traitor.

Correctness

We can use knowledge trees to show the correctness of the Byzantine Generals algorithm. Consider an arbitrary loyal general, say, Leo. Whatever plan X that Leo chooses, he correctly relays it to the other generals. The other loyal generals correctly report it to each other as X, though the traitor Zoe can report it as arbitrary plans Y and Z. Here is the knowledge tree about Leo that results:

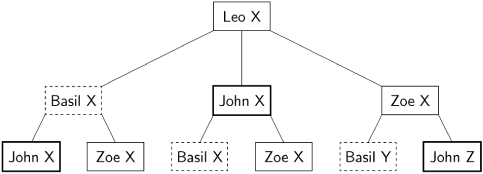
From the tree it is easy to see that both John (thick frames) and Basil (dashed frames) each received two reports that Leo chose X. Therefore, the messages Y and Z cannot influence their votes.

Let us now examine the knowledge tree about the traitor Zoe, who can choose to send first-round messages with arbitrary plans X, Y and Z to the other three generals:

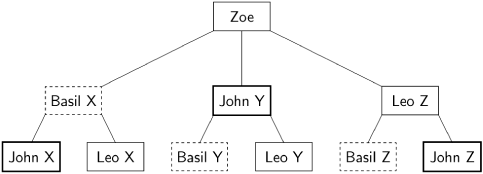
The contents of these messages are accurately relayed by the loyal generals during the second round. As you can see in the diagram, all three generals received exactly one each of the plans X, Y and Z; therefore, they all come to the same conclusion about the plan of Zoe.

Complexity

The Byzantine Generals algorithm can be generalized to any number of generals. For every additional traitor, an additional round of messages must be sent. The total number of generals must be at least 3t + 1, where t is the number of traitors.

The total number of messages sent by each general is (n − 1) + (n − 1) · (n − 2) + (n − 2) · (n − 3) + · · ·, because it sends its plan to every other general (n − 1), a second-round report of each of the (n − 1) generals to (n − 2) generals, and so on. The total number of messages is obtained by multiplying this by n, the number of generals, giving:

As can be seen from the following table, the algorithm quickly becomes impractical as the number of traitors increases:

traitors	generals	messages
1	4	36
2	7	392
3	10	1790
4	13	5408

There is a very simple algorithm for consensus in the presence of crash failures. The idea is for each general to send over and over again the set of plans that it has received:

planType finalPlan
set of planType plan ← { chooseAttackOrRetreat }
set of planType receivedPlan

p1:  do t + 1 times
p2:     for all other generals G
p3:        send(G, plan)
p4:     for all other generals G
p5:        receive(receivedPlan)
p6:        plan ← plan ∪ receivedPlan
p7:  finalPlan ← majority(plan)

It is sufficient that a single such message from a loyal general reach every other loyal general, because once a loyal general has determined the plan of another loyal general, it retains that information. If there are t + 1 rounds of sending and receiving messages in the presence of at most t traitors, then one such message must have been sent and received without crashing.

Let us examine how the algorithm works with four nodes—two of whom traitors—and three rounds. The following diagram shows a portion of the knowledge tree about Leo, assuming that no processes crash. There is not enough room to display the entire tree, so we display only those nodes that affect the decision of an arbitrary loyal general Zoe about Leo:

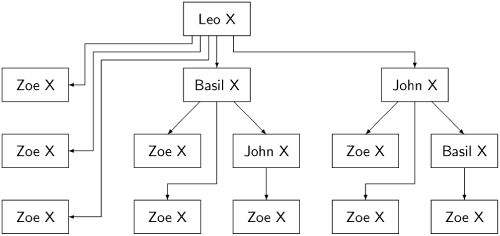
Leo chooses X. Each row below the box for Leo shows the messages sent and received during a round. In the first round, Leo sends his plan to the other three generals. Basil and John receive Leo’s plan and send it to Zoe. In the third round, Leo’s plan is still stored in the sets plan for Basil and John, so they both send it again to Zoe. On the left, we see the messages that Zoe receives directly from Leo on the three rounds.

Is there a scenario in which at most two out of the three generals Leo, Basil and John crash, and Zoe cannot determine the plan of Leo? If not, then since Zoe and Leo were chosen arbitrarily, this implies that all loyal generals receive the same set of plans and can come to a consensus by majority vote.

We will make the assumption that no general crashes immediately after activation or after receiving a message without sending at least one message. The algorithm still works and we leave it as an exercise to extend the proof of correctness for these cases.

Leo sends at least one message; if he sends a message to Zoe before crashing, then Zoe knows his plan and correctness follows. If not, suppose that one of these messages went to Basil. The knowledge tree about Leo is a subtree of the tree shown in the following diagram:

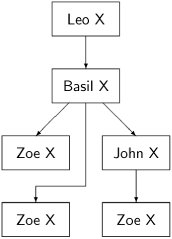
In the second round, if Basil sends a message to Zoe, all is well, and we don’t care if he crashes immediately afterwards, or if he never crashes and it is John who is the second traitor. However, Basil may send a message to John and then crash before sending a message to Zoe. The following diagram results:

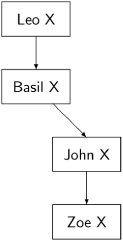
But we have already “used up” the two traitors allowed in the statement of the problem, so John must be loyal and he sends Leo’s plan to Zoe.

It can be proved [48, Section 6.2] that for any number of nodes of which t are subject to crash failure, the algorithm reaches consensus in t + 1 rounds. The idea of the proof is similar to the argument for four generals and two traitors: since there are more rounds than traitors, a loyal general must eventually send the set of plans it knows to all other generals, and from then on, the loyal generals exchange this information in order to reach consensus.

The Byzantine Generals algorithm requires a large number of messages, especially as the number of traitors (and thus generals) increases. In this section, we describe another algorithm for consensus, the King algorithm, which uses many fewer messages. However, the algorithm requires an extra general per traitor, that is, the number of generals n must be at least 4t + 1, where t is the number of traitors, instead of the 3t + 1 required by the Byzantine Generals algorithm. We will present the algorithm for the simplest case of one traitor and 4 · 1 + 1 = 5 generals. The algorithm is based upon the fact that a small number of traitors cannot influence the final vote if there is an overwhelming majority for one plan. If there are four loyal generals and the vote is 4–0 or 3–1, then the single traitor cannot influence the outcome. Only if the vote is tied at 2–2 can the traitor cause consensus to fail by sending A to some generals and R to others.

The algorithm is called the King algorithm because in each round one of the generals is given a special status as a king whose vote is more important than the vote of the other generals. To preserve the distributed nature of the algorithm, we will not assume that the identity of the king is known to all other nodes. All we need is that each node knows whether it is or is not a king on any particular round. Furthermore, to preserve the property that the system be fault-tolerant under arbitrary failure, we will not assume that the king node does not fail. That is, whatever method is used to designate the king, it is possible that the king will be a traitor.

However, if two generals take the role of king one after the other, then we are assured that at least one of them will be loyal. When a loyal general is king, he will cause the other generals to come to a consensus. If he is the second king, the final vote will be according to that consensus. If he is the first king, the loyal generals will have an overwhelming majority in favor of the consensus, so that even if the second king is the traitor, he cannot cause the loyal generals to change their plans.

Algorithm 12.4 is the King algorithm. As before, each general chooses a plan and sends it to each other general. After receiving all these messages, each general has five plans and stores the result of a majority vote in myMajority. In addition, the number of votes for the majority (3, 4 or 5) is stored in the variable votesMajority.

The second round starts with the king (only) sending his plan to the other generals. The choice of a king is decided according to some arbitrary, but fixed, algorithm executed by all the generals; for example, the generals can be ordered in alphabetical order and the king chosen according to this order. When a node receives the king’s plan, it checks votesMajority, the number of votes in favor of myMajority; if the majority was overwhelming (greater than ⌊n/2⌋ +t, here greater than 3), it ignores the king’s plan, otherwise, it changes its own plan to the king’s plan.

planType finalPlan, myMajority, kingPlan
planType array[generals] plan
integer votesMajority, kingID

p1:  plan[myID] ← chooseAttackOrRetreat

p2:  do two times
p3:     for all other generals G       // First and third rounds
p4:        send(G, myID, plan[myID])
p5:     for all other generals G
p6:        receive(G, plan[G])
p7:     myMajority ← majority(plan)
p8:     votesMajority ← number of votes for myMajority

p9:     if my turn to be king          // Second and fourth rounds
p10:       for all other generals G
p11:          send(G, myID, myMajority)
p12:       plan[myID] ← myMajority
        else
p13:       receive(kingID, kingPlan)
p14:       if votesMajority > 3
p15:          plan[myID] ← myMajority
           else
p16:          plan[myID] ← kingPlan

p17: finalPlan ← plan[myID]       // Final decision

Finally, the entire algorithm is executed a second time during which the king will be a different general.

Let us work through an example. We need five generals, so Mike will join as the fifth general, and we will assume that he is the traitor, so that we are only interested in the data structures of the other four generals. Let us suppose that the initial plans are evenly divided, with Basil and John choosing attack and Leo and Zoe choosing retreat. Let us further suppose that the traitor Mike sends attack to two of the generals and retreat to the other two in an attempt to foil the consensus. Upon completion of the first round, the data structures will be as follows:

Consider the case where the first king is a loyal general, say Zoe. Zoe sends R, her myMajority; since no general had computed its myMajority with an overwhelming majority (votesMajority>3), they all change their own plans to be the same as the king’s:

In the third round, the plans are sent again and the variables myMajority and votes-Majority recomputed:

We have not shown the messages sent by the traitor Mike; regardless of what he sends, all the loyal generals agree that all of them have chosen R, so they all set myMajority to R and votesMajority to four (or five if the traitor happened to send R). Both four and five votes are considered an overwhelming majority, so it doesn’t matter if the king in the fourth round is a traitor or not, because his plan will be ignored, and all the loyal generals will come to a consensus on R.

Consider now the case where the first king is the traitor Mike. In his role as king, the traitor Mike can, of course, send any messages he wants:

During the third round, the plans are again exchanged and the votes recomputed, resulting in the following data structures:

All loyal generals have the same set of plans tied at two so, clearly, whatever messages the traitor sends will affect the value of myMajority at each node. But regardless of whether myMajority is for A or R, for each loyal general votesMajority will be three, that is, the choice is not overwhelming. Now the general chosen to be king in the fourth round will be a loyal general, say Zoe, so whatever Zoe sends as the king’s plan, say A, will be adopted by all the other loyal generals in statement p16: plan[myID]←kingPlan:

These plans become the final plans, so they come to a consensus on A.

It can be proved [48, Section 6.4] that there is no algorithm that achieves consensus in the presence of byzantine failures when the number of generals is less than 3t+1. Let us use knowledge trees to prove this for t = 1.

Example 12.3. Theorem

With three generals, one of whom is a traitor, it is impossible to achieve consensus in the presence of Byzantine failures.

Proof: We first define what we mean by an algorithm for this problem. We assume that each general chooses a plan and sends one or more messages. For a loyal general, the messages it sends are either the plan that it chose or the plan received from another general. A traitor is allowed to send any messages whatsoever. We do not specify the number of rounds or the number of messages per round, but it doesn’t really matter, because any message coming directly from a loyal general is correct and any message coming from a traitor can be arbitrary by the assumption of byzantine failures.

Let us assume that John is the traitor, that Zoe and Leo are loyal and they choose X and Y respectively. The knowledge trees for Zoe and Leo are:

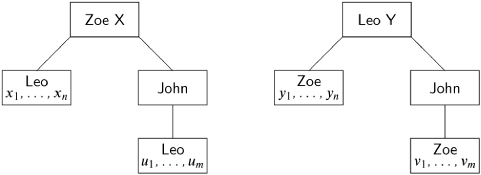
The decision by a loyal general is made applying a function f to the set of plans stored in local data or received as messages. For any algorithm to work, a loyal general must correctly infer the plans of the other loyal generals, so it must be true that:

Equation 12.1. 

Equation 12.2. 

whatever the values of the sets {u₁,. . ., u_m} and {v₁,. . ., v_m}.

Zoe and Leo must also come to a consensus on a plan for John. John sends a set of messages to Zoe and another set to Leo; both loyal generals relay the messages to the other. By “maliciously” choosing messages to send, the traitor can cause its knowledge tree to be:

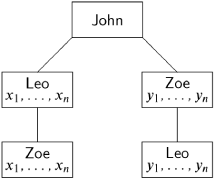
Substituting {y₁,. . ., y_n} for {u₁,. . ., u_m} in (12.1) shows that Leo decides

f ({x₁,. . ., x_n} ∪ {y₁,. . ., y_n}) =X,

and substituting {x₁,. . ., x_n} for {v₁,. . ., v_m} in (12.2) shows that Zoe decides

f ({y₁,. . ., y_n} ∪ {x₁,. . ., x_n}) =Y.

Consensus is not achieved.