Chapter 4: L(2, 1) - Labeling on Jahangir Graph

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

U. M. Prajapati

Department of Mathematics,
St. Xavier’s College,
Ahmedabad, Gujarat (INDIA)
E-mail: [email protected]

N. B. Patel

Department of Mathematics,
Gujarat University,
Ahmedabad, Gujarat (INDIA)
E-mail: [email protected]

L(2, 1) - labeling problems consist of an assignment of non-negative integers to the nodes of a graph such that the adjacent nodes have labels which differ by at least two, and the nodes at distance two must have different labels. The span of L(2, 1) - labeling is the difference between the minimum and maximum labels which are assigned to the nodes. The minimum span is called L(2, 1)-labeling number or λ - number. In this chapter, L(2, 1)-labeling number of Jahangir graph (J_n,m) for n ≥ 3 and m ≥ 5 is discussed.

4.1Introduction

A frequency assignment problem was given by Hale [1], in order to assign a frequency (non-negative integer) to each TV or radio transmitter, located at various places such that communication does not interfere. Hale [1] introduced the notion of T-coloring of a graph in 1980, to formulate the frequency assignment problem as a graph coloring problem. In 1988, Roberts proposed a variation of the frequency assignment problem in which close transmitters must receive frequencies that are at least two apart. In a graph model of this problem, the transmitters are represented by the nodes of a graph. Two nodes are very close if they are adjacent in the graph and close if they are at a distance two apart in the graph. Motivated by the problem of assigning frequency to radio or TV transmitters, Griggs and Yeh [2] introduced L(2, 1)-labeling in 1992. For standard terminology Bondy and Murty [3] is used. For a detailed survey on graph labeling we refer to [4] is refered. Griggs and Yeh [2] showed that the L(2, 1) - labeling problem is NP-complete for general graphs and determined the exact values of λ(P_n), λ(C_n) and λ(W_n). He also showed that for n-cube Q_n, λ(Q_n) ≤ 2n + 1 for n ≥ 5; for a tree T with maximum degree Δ ≥ 1, λ(T) is either Δ + 1 or Δ + 2; for a general graph G with maximum degree Δ, λ(G) ≤ Δ² + 2Δ; for 3 - connected graph G, λ(G) ≤ Δ² + 2Δ − 3; for a graph G of diameter - 2 graph, λ(G) ≤ Δ². In 1996, Chang and Kuo [5] improved the upper bound for general graph G with maximum degree Δ, i.e λ(G) ≤ Δ² + Δ. He also provided polynomial-time algorithm for the L(2, 1) - labeling problem on trees. In 2004, Kuo and Yan [6] have studied the L(2, 1) - labeling problem for the cartesian products of paths and cycles. In 2011, Vaidya and Bantva [7] have proved the λ - number of an n - ary, Δ - regular cactus is Δ + 1 or Δ + 2, $λ (C_{n}^{k}) = 2 k + 1$ where $C_{n}^{k}$ is the one point union of k cycles C_n. In 2016, Baby Smitha [8] and K. Thirusangu have determined the L(2, 1) - labeling number for the line graph of triangular snake graph and spiked snake graphs. In 2019, Prajapati and Patel [10] have determined the L(2, 1) - labeling number λ(G) for the line graph of a crown graph and the line graph of an armed crown graph.

4.2Definitions

Definition. An L(2, 1) - labeling of graph G with V(G) and E(G) as vertex set and edge set respectively, is a function $f : V (G) \to {0} \cup N$ such that for every pair of vertices x and y the following condition must be satisfied:

1. If d(x, y) = 1 then $∥ f (x) - f (y) ∥ \geq 2$ and

2. If d(x, y) = 2 then $∥ f (x) - f (y) ∥ \geq 1$ ,

where d(x, y) denotes the distance between x and y. The L(2,1) - labeling number of G, denoted by λ(G), is the smallest number k such that G admits an L(2,1) - labeling with maximum label k.

As bandwidth is a limited resource, the main target in FAP is to come up with a frequency assignment using a minimum number of frequencies, i.e. one needs to minimize the span of the labeling proposed. For convenience, without loss of generality, the smallest label is considered to be zero, so that the span is the highest label assigned.

In this chapter, L(2,1) - labeling of a generalized Jahangir graph which has been introduced by Ali et al. [9] is discussed.

Definition. Jahangir graph J_n,m for m ≥ 3 and n ≥ 2 is a graph on nm + 1 vertices consisting of a cycle C_nm with one additional vertex which is adjacent to m vertices of C_nm at distance n to each other on C_nm.

Jahangir graph J_2,8 appears on Jahangir’s tomb in his mausoleum. It is situated 5 km northwest of Lahore, Pakistan, across the River Ravi.

Remark. Wheel graph W_n and gear graph G_n are special cases of J_n,m for n = 1 and n = 2 respectively.

Definition. The region between the edge formed by joining central vertex to vertices on C_nm at distance n from each other is known as petals of J_n,m. Let P_m be the petal formed by v₀v_i,0v_i+1,0 (mod m) for 1 ≤ i ≤ m i.e P_i = v₀ v_i,0 v_i+1,0 (mod m) for 1 ≤ i ≤ m. Each petal has a path of even or odd length.

Notation. In J_n,m, v₀ is adjacent to v_i,0 for 1 ≤ i ≤ m which are at distance n from each other and P_i = v₀ v_i,0 v_i+1,0 (mod m). The vertex set of J_n,m is $V (J_{n, m}) = {v_{i, 0} | 1 \leq i \leq m} \cup {v_{i, j} | 1 \leq i \leq m, 1 \leq j \leq n - 1} \cup {v_{0}}$ and the edge set of J_n,m is $E (G) = {v_{0} v_{i, 0} | 1 \leq i \leq m} \cup {v_{i, 0} v_{i, 1} | 1 \leq i \leq m} \cup {v_{i, n - 1} v_{i + 1, 0} | 1 \leq i \leq m} \cup {v_{i, j} v_{i, (j + 1)} | 1 \leq i \leq m, 1 \leq j \leq n - 2}$ . To form J_n,m join v_i,j to v_i,j+1 for 1 ≤ i ≤ m and o ≤ j ≤ n − 2 and join v_i,n−1 to v_i+1,0 (mod m) for 1 ≤ i ≤ m. So the distance between the vertices is d(v₀, v_i,0) = 1 for 1 ≤ i ≤ m; d(v_i,0, v_j,0) = 2 for 1 ≤ i and j ≤ m with i ≠ j; d(v_i,0, v_i,1) = 1 for 1 ≤ i ≤ m; d(v_i,n−1, v_i+1,0 (mod m)) = 1 for 1 ≤ i ≤ m; d(v_i,j, v_i,j+1) = 1 for 1 ≤ i ≤ m and 1 ≤ j ≤ n − 2. J_n,m for n = 4 and m = 4 can be shown in the Figure 4.1

4.3Labeling Number of Generalized Jahangir Graph

Theorem 4.1

For m ≥ 5 and n ≡ 0 (mod 3), λ(J_n,m) ≤ m + 1.◼

Proof. In J_n,m, v₀ is adjacent to v_i,0 for 1 ≤ i ≤ m which are at distance n from each other and P_i = v₀ v_i,0 v_i+1,0 (mod m). Define $f : V (G) \to N \cup {0}$ as follows:

\begin{aligned} f (v_{0}) & = 0; \\ f (v_{i, 0}) & = i + 1 for 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, j - 1}) + 1 (mod m + 1)) + 1 for 1 \leq j \leq 2, 1 \leq i \leq m - 1; \\ f (v_{m, 1}) & = f (v_{m, 0}) (mod m + 1)) + 1; \\ f (v_{m, 2}) & = f (v_{m, 1}) + 3 (mod m + 1)) + 1; \\ f (v_{i, j}) & = f (v_{i, 0}) for j \equiv 0 (mod 3), 3 \leq j \leq n - 1, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, 1}) for j \equiv 1 (mod 3), 3 \leq j \leq n - 1, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, 2}) for j \equiv 2 (mod 3), 3 \leq j \leq n - 1, 1 \leq i \leq m . \end{aligned}

Hence λ(J_n,m) ≤ m + 1 for m ≥ 5 and n ≡ 0 (mod 3).□

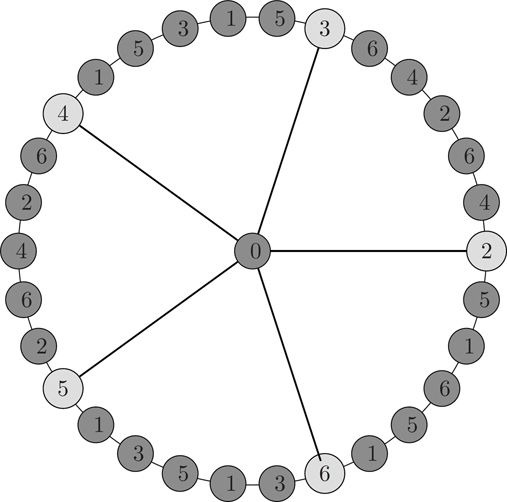
Illustration 4.3.1. The L(2, 1) - labeling of J_6,5 is shown in Figure 4.2.

Theorem 4.2

For m ≥ 5 and n ≡ 1 (mod 3), λ(J_n,m) ≤ m + 1.◼

Proof. Define $f : V (G) \to N \cup {0}$ as follows:

\begin{aligned} f (v_{0}) & = 0; \\ f (v_{i, 0}) & = i + 1 for 1 \leq i \leq m; \end{aligned}

Now, we take different cases:

Case-1: If m = 5 then define

\begin{aligned} f (v_{1, 1}) & = f (v_{1, 0}) + 1 (mod m + 1)) + 1; \\ f (v_{1, 2}) & = f (v_{1, 1}) + 1 (mod m + 1)) + 1; \\ f (v_{1, n - 1}) & = f (v_{1, n - 2}) + 1 (mod m + 1)); \\ f (v_{i, 1}) & = f (v_{i, 0}) + 1 (mod m + 1)) + 1, 2 \leq i \leq 3; \\ f (v_{i, 2}) & = f (v_{i, 1}) + 1 (mod m + 1)), 2 \leq i \leq 3; \\ f (v_{i, n - 1}) & = f (v_{i, n - 2}) + 1 (mod m + 1)) + 1, 2 \leq i \leq 3; \\ f (v_{4, 1}) & = f (v_{4, 0}) + 1 (mod m + 1)) + 1; \\ f (v_{4, 2}) & = f (v_{4, 1}) + 2 (mod m + 1)) + 1; \\ f (v_{4, n - 1}) & = f (v_{4, n - 2}) + 3 (mod m + 1)) + 1; \\ f (v_{5, 1}) & = f (v_{5, 0}) + 1 (mod m + 1)); \\ f (v_{5, 2}) & = f (v_{5, 1}) + 1 (mod m + 1)) + 1; \\ f (v_{5, n - 1}) & = f (v_{5, n - 2}) + 1 (mod m + 1)) + 1; \\ f (v_{i, j}) & = f (v_{i, 0}) for j \equiv 0 (mod 3), 3 \leq j \leq n - 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, 1}) for j \equiv 1 (mod 3), 3 \leq j \leq n - 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, 2}) for j \equiv 2 (mod 3), 3 \leq j \leq n - 2, 1 \leq i \leq m . \end{aligned}

Case-2: If m ≥ 6 then define

\begin{aligned} f (v_{i, j}) & = f (v_{i, j - 1}) + 1 (mod m + 1)) + 1 for 1 \leq j \leq 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, 0}) for j \equiv 0 (mod 3), 3 \leq j \leq n - 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, 1}) for j \equiv 1 (mod 3), 3 \leq j \leq n - 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i, 2}) for j \equiv 2 (mod 3), 3 \leq j \leq n - 2, 1 \leq i \leq m; \\ f (v_{i, n - 1}) & = f (v_{i, n - 2}) + 1 (mod m + 1)) + 1, 1 \leq i \leq m . \end{aligned}

Hence λ(J_n,m) ≤ m + 1 for m ≥ 5 and n ≡ 1 (mod 3).□

Illustration 4.3.2. The L(2,1) - labeling of J_7,6 is shown in the Figure 4.3.

Theorem 4.3

For m ≥ 5 and n ≡ 2 (mod 3), λ(J_n,m) ≤ m + 1.◼

Proof. Define $f : V (G) \to N \cup {0}$ as follows:

\begin{aligned} f (v_{0}) & = 0; \\ f (v_{i, 0}) & = i + 1 for 1 \leq i \leq m; \end{aligned}

Now take different cases:

Case-1: If m = 5 then define

\begin{aligned} f (v_{i, j}) & = f (v_{i, j - 1}) + 3 (mod m + 1)) + 1 for 1 \leq j \leq 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 0) for j \equiv 0 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 1) for j \equiv 1 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 2) for j \equiv 2 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, n - 1}) & = f (v_{i, n - 2}) + 3 (mod m + 1)) + 1, 1 \leq i \leq m; \\ f (v_{i, n - 2}) & = f (v_{i, n - 3}) + 3 (mod m + 1)) + 1, 1 \leq i \leq m . \end{aligned}

Case-2: If m = 6 then define

\begin{aligned} f (v_{i, j}) & = f (v_{i, j - 1}) + 1 (mod m + 1)) + 1 for 1 \leq j \leq 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 0) for j \equiv 0 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 1) for j \equiv 1 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 2) for j \equiv 2 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, n - 2}) & = f (v_{i, n - 1}) + 2 (mod m + 1)) + 1, 1 \leq i \leq m; \\ f (v_{i, n - 1}) & = f (v_{i, n - 2}) + 4 (mod m + 1)) + 1, 1 \leq i \leq m . \end{aligned}

Case-3: If m = 7 then define

\begin{aligned} f (v_{i, j}) & = f (v_{i, j - 1}) + 1 (mod m + 1)) + 1 for 1 \leq j \leq 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 0) for j \equiv 0 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 1) for j \equiv 1 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 2) for j \equiv 2 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, n - 2}) & = f (v_{i, n - 1}) + 3 (mod m + 1)) + 1, 1 \leq i \leq m; \\ f (v_{i, n - 1}) & = f (v_{i, n - 2}) + 4 (mod m + 1)) + 1, 1 \leq i \leq m . \end{aligned}

Case-4: If m ≥ 8 then define

\begin{aligned} f (v_{i, j}) & = f (v_{i, j - 1}) + 1 (mod m + 1)) + 1 for 1 \leq j \leq 2, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 0) for j \equiv 0 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 1) for j \equiv 1 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, j}) & = f (v_{i}, 2) for j \equiv 2 (mod 3), 3 \leq j \leq n - 3, 1 \leq i \leq m; \\ f (v_{i, n - 2}) & = f (v_{i, n - 1}) + 1 (mod m + 1)) + 1, 1 \leq i \leq m; \\ f (v_{i, n - 1}) & = f (v_{i, n - 2}) + 1 (mod m + 1)) + 1, 1 \leq i \leq m . \end{aligned}

Hence λ(J_n,m) ≤ m + 1 for m ≥ 5 and n ≡ 2 (mod 3).□

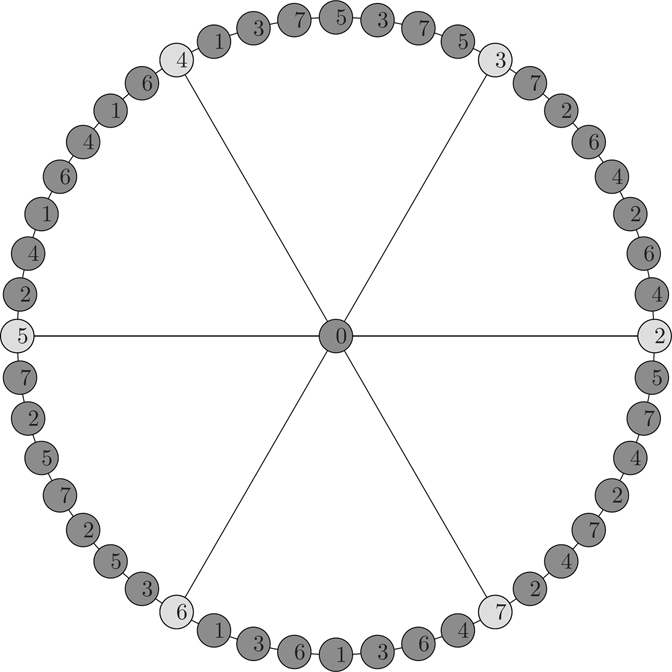
Illustration 4.3.3. The L(2,1) - labeling of J_8,6 is shown in Figure 4.4.

Theorem 4.4

The L(2,1) - labeling number of J_n,m for m ≥ 5 and n ≥ 3 is m + 1.◼

Proof. Define $f : V (G) \to N \cup {0}$ such that f(v₀) = 0. Since d(v₀, v_i,0) = 1 for 1 ≤ i ≤ m, in order to preserve L(2,1) - labeling, f(v_1,0) ≥ 2 is assumed. Now according to the definition of L(2,1) - labeling, if the distance between any two vertices is 2 then the label must differ by at least 1. Since f(v_1,0) ≥ 2 there are m − 1 remaining vertices $v_{2, 0}, v_{3, 0}, \dots, v_{m, 0}$ which have to be labeled. By labeling the remiaing m − 1 vertices consecutively, one of the vertices will get a label greater than or equal to (m − 1) + 2. Thus λ(J_n,m) ≥ m + 1 for m ≥ 5 and n ≥ 3. Now, from the Theorems 4.1 to 4.3, it can be concluded that λ(J_n,m) ≤ m + 1 for m ≥ 5 and n ≥ 3. Hence λ(J_n,m) = m + 1 for m ≥ 5 and n ≥ 3.

4.4Conclusion□

Exact L(2,1) - labeling number for a generalized Jahangir graph J_n,m is computed for m ≥ 5 and n ≥ 3. A lots of work has been done in this area and still work is being carried out for different graphs. Determination of an exact L(2,1)-labeling number for other graph families is an open area of research.

References

1.W. K. Hale. Frequency assignment: Theory and applications. Proc. IEEE, 68(12): 1497-1514, 1980.

2.J. R. Griggs and R. K. Yeh. Labeling graphs with condition at distance two. SIAM J. Discrete Math., 5(4): 586-595, 1992.

3.J. A. Bondy and U. S. R. Murty. Graph Theory with Applications (2nd Edition). McMillan, New York, 1976.

4.J. A. Gallian. A dynamic survey of graph labeling. The Electronic Journal of Combinatories, #DS6, 1-518, 2019.

5.G. J. Chang and D. Kuo. The L(2,1)-labeling problem on graphs. SIAM J. Discrete Math., 9(2): 309-316, 1996.

6.D. Kuo, and J. Yan. On L(2,1) - labelings of cartesian products of paths and cycles. Discrete Math. 283, 137-144, 2004.

7.S. K. Vaidya and D. D. Bantva. Labeling cacti with a condition at distance two. Le Matematiche, 66(1): 29-36, 2011.

8.Baby Smitha, K. M. and K. Thirusangu. Distance two labeling of certain snake graphs. International Mathematical Forum, 11(11): 503-512, 2016.

9.K. Ali, E. T. Baskoro and Tomescu I. On the Ramsey numbers for paths and generalized Jahangir graphs J_s,m. Bull. Math. Soc. Sci. Math., 51: 177-182, 2008.

10.U. M. Prajapati and N. B. Patel. L(2,1) labeling of line graph of some graphs. Journal of Applied Science and Computations, 6(5): 309-316, 2019.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 4: L(2, 1) - Labeling on Jahangir Graph

Create new playlist

Sign In

Sign Up

Table of Contents for
Chapter 4: L(2, 1) - Labeling on Jahangir Graph