13.1Introduction

We consider here only undirected, connected and simple graph G = (V(G), E(G)) with the vertex set V(G) and edge set E(G). For various graph theoretic notations and terminology we follow Gross and Yellen [4] and D. M. Burton[1] for number theoretic results.

The notion of a prime labeling originated with Roger Entringer and was introduced in a paper by Tout et al.[12]. Many researchers have studied prime labeling for a good number of graphs listed in [3].

In [2, 5], Hunter Lehmann et al. defined a beautiful ordering in Gaussian integers and named it as “spiral ordering in Gaussian integers”. Motivated by prime labeling they introduced Gaussian prime labeling of graphs with respect to spiral ordering. So, Gaussian prime labeling is an extension of prime labeling.

We will start our discussion by giving some definitions starting from spiral ordering of Gaussian integers and its properties given by Steven Klee et al. [5].

13.1.1Spiral Ordering of the Gaussian Integers

Gaussian integers are complex numbers of the form γ = x + iy where x and y are integers and i² = −1. The set of Gaussian integers is usually denoted by Z[i]. A Gaussian integer γ is said to be an even Gaussian integer if γ is divisible by 1 + i and otherwise is called an odd Gaussian integer. The norm on Z[i] is defined as d(x + iy) = x² + y². One can easily see that the only units of Z[i] are ±1, ± i. The associates of Gaussian integer γ are unit multiples of γ. In Z[i], two Gaussian integers are relatively prime if their common divisors are the only units of Z[i]. A Gaussian integer γ is said to be a prime Gaussian integer if and only if ±1, ± i, ± γ, ± iγ are the only divisors of γ.

In [2, 5], the recursion relation of spiral ordering of the Gaussian integers starting with γ₁ = 1 is defined as follows:

The notation γ_n is used to denote the n^th Gaussian integer under the above ordering. We symbolically write first ′n′ Gaussian integers by [γ_n]. The index of Gaussian integer x + iy in the spiral ordering is denoted by I(x + iy).

In [5] Steven Klee et al. established some interesting basic properties about Gaussian integers with the above ordering like:

1.Any two consecutive Gaussian integers are relatively prime.

2.Any two consecutive odd Gaussian integers are relatively prime.

3.γ and γ + μ are relatively prime, if γ is a Gaussian integer and μ is a unit.

4.γ and γ + μ(1 + i)^k are relatively prime, if γ is an odd Gaussian integer and μ is a unit. where k is a positive integer.

5.γ and γ + π are relatively prime if and only if π does not divide γ where γ is a Gaussian integer and π is a prime Gaussian integer.

Definition. [2, 5] Let G be a graph having n vertices. A bijective function g:V(G) → [γ_n] is called Gaussian prime labeling, if the images of adjacent vertices are relatively prime. A graph which admits Gaussian prime labeling is known as a Gaussian prime graph.

Hunter Lehmann and Andrew Park proved that any tree with ≤72 vertices is a Gaussian prime tree in [2]. In [5] Steven Lee et al. proved that n-centipede tree, (n, 2) −centipede tree, path graph, spider tree, star graph, (n, 3) firecracker tree, (n, k, m) double star tree are Gaussian prime graphs.

Deretsky, Lee and Mitchem defined a dual of prime labeling named vertex prime labeling as follows.

Definition. [13] A graph with edge set E has a vertex prime labeling if its edges can be labeled with distinct integers 1, 2, …, |E| such that for each vertex of degree at least 2 the greatest common divisor of the labels on its incident edges is 1.

Deretsky, Lee and Mitchem[13] proved that forests, all connected graphs, C2k⋃Cn, C2m⋃C2n ⋃C2k+1, C2m⋃C2n⋃C2t⋃Ck, and 5C_2m are vertex prime graphs. They further proved that a graph with exactly two components, one of which is not an odd cycle, has a vertex prime labeling and a 2-regular graph with at least two odd cycles does not have a vertex prime labeling. Here, we introduce Gaussian vertex prime labeling with respect to spiral ordering motivated by Gaussian prime labeling and vertex prime labeling.

Definition. A graph with edge set E has a Gaussian vertex prime labeling if its edges can be labeled with first |E| Gaussian integers γ₁, γ₂, …, γ_|E| such that for each vertex of degree at least 2 the greatest common divisor of the labels on its incident edges is unit. A graph which admits Gaussian vertex prime labeling is called a Gaussian vertex prime graph.

13.1.2Origami Models

Origami is a paper folding art associated with Japanese culture. The word origami originates from two Japanese words “ori” and “kami” where “ori” represents folding and “kami” represents paper, here kami changes to gami due to rendaku. An origami practitioner’s goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques without use of glue, cuts and markings on the paper. The Japanese word “kirigami” refers to designs which use cuts.

The Miura fold is a form of rigid origami(a branch of origami which is concerned with folding structures using flat rigid sheets joined by hinges). The Miura fold has a lot of practical applications. Let us see some of them for examples. Large solar panel arrays for space satellites in the Japanese space program have been Miura folded before launch and then spread out in space. Flat foldable furniture is another application. Miura fold has applications in surgical devices such as stents. Also University of Fribourg used this fold to stack hydrogel films, generating electricity similarly to electric eels.

The following definitions of graphs, inspired from origami models is given by U. M. Prajapati and R. M. Gajjar. And they have studied various labeling techniques for these graphs. We denote the set {1,2,…,n} by [n].

Definition. [6] Let a₀ be the apex vertex and a₁, a₂, …, a_n−1, a_n be consecutive n rim vertices of wheel graph W_n, n ≥ 3; let b₁, b₂, b₃, …, b_2n−1, b_2n be consecutive 2n vertices of cycle C_2n; let c₁, c₂, c₃, …, c_2n−1, c_2n be consecutive 2n vertices of cycle C_2n. Join each a_i to b_2i−1 by an edge and b_2i to c_2i by an edge. Take a new vertex d_i; Join each d_i to c_2i−1 and c_2i+1 by an edge, for each i ∈ [n], subscripts are taken modulo n. The resulting graph is called a braided star graph BRS_n.

Definition. [7] Let v₁, v₂, …, v_4n−1, v_4n be consecutive 4n vertices of cycle C_4n, n ≥ 3. Let u₀ be the central vertex and u₁, u₂, …, u_2n−1, u_2n be end vertices of star K_1,2n. Now join u₀ to v_4i−3 by an edge; join u_2i−1 to v_4i−2 and u_2i by an edge, for each i ∈ [n]. The resulting graph is called a holiday star graph HS_n.

Definition. [8] Let v₀ be the apex vertex and v₁, v₂, v₃, …, v_2n−1, v_2n be consecutive 2n rim vertices of wheel graph W_2n, n ≥ 3. Subdivide spoke edge v₀v_2i−1 with vertex w_i and at each w_i, join two copies of the path of length 2; P2l=v0,u2i−1,wi and P2r=v0,u2i,wi for each i ∈ [n]. The resulting graph is called the kusudama flower graph KF_n.

Definition. [9] Let u₀ be the apex vertex and v₁, v₂, v₃, …, v_4n−1, v_4n be consecutive 4n rim vertices of wheel graph W_4n, n ≥ 3. Subdivide the edge u₀v_2i−1 by a vertex u_i, for i ∈ [2n]. The resulting graph is called the Christmas star graph CS_n.

Definition. [10] Let a₀ be the central vertex and a₁, a₂, …, a_n−1, a_n be end vertices of star K_1,n; let b₁, b₂, b₃, …, b_2n−1, b_2n be consecutive 2n vertices of cycle C_2n, n ≥ 3; let c₁, c₂, c₃, …, c_2n−1, c_2n be consecutive 2n vertices of cycle C_2n. Join each a_i to b_2i−1 and b_2i+1 by an edge; join each b_2i to c_2i by an edge. Take a new vertex d_i; join each d_i to c_2i−1 and c_2i+1 by an edge, for each i ∈ [n], subscripts are taken modulo n. The resulting graph is called the Boreale star graph BLS_n.

Definition. [11] Let u₀ be the apex vertex and v₁, v₂, v₃, …, v_4n−1, v_4n be consecutive 4n rim vertices of wheel graph W_4n, n ≥ 3. A new vertex u_i; join each u_i to v_2i and u₀ by an edge, for each i ∈ [2n]. The resulting graph is called the cherry blossom graph CB_n.

Throughout this chapter, we will understand that the graph that is Gaussian vertex prime means that it is a Gaussian vertex prime graph with respect to the spiral ordering of Gaussian integers.

13.2Main Results

Theorem 13.1

Boreale star graph BLS_n is Gaussian vertex prime.◼

Proof. For the graph BLS_n, V(BLSn)={a0}∪{ai,di|i∈[n]}∪{bi,ci|i∈[2n]} and E(BLSn)={a0ai,aib2i−1,b2ic2i,c2i−1di|i∈[n]}∪{bibi+1,cici+1|i∈[2n−1]}∪{aib2i+1,dic2i+1|i∈[n−1]}∪{anb1,c2nc1,b2nb1,dnc1}

Here, |V(BLS_n)| = 6n + 1 and |E(BLS_n)| = 10n

Define a bijection f:E(BLS_n) → [γ_10n] as follows:

Let v be an arbitrary vertex of BLS_n. We prove f is a Gaussian vertex prime labeling of BLS_n by considering the following cases:

If v = a₀, gcd(f(a₀a₁), f(a₀a₂), …, f(a₀a_n)) = gcd(γ₁, γ₁₁, …, γ_10n−1) = 1

If v = a_i,

gcd(f(a_ia₀), f(a_ib_2i+1), f(a_ib_2i−1)) = gcd(γ_10i−9, γ_10i−7, γ_10i−8) = 1, i ∈ [n − 1]

If v = a_n,

gcd(f(a_na₀), f(a_nb₁), f(a_nb_2n−1)) = gcd(γ_10n−9, γ_10n−7, γ_10n−8) = 1

If v = b_2i,

gcd(f(b_2ib_2i+1), f(b_2ib_2i−1), f(b_2ic_2i)) = gcd(γ_10i−5, γ_10i−6, γ_10i−4) = 1, i ∈ [n − 1]

If v = b₁,

gcd(f(b₁b₂), f(b₁b_2n), f(a₁b₁), f(a_nb₁)) = gcd(γ₄, γ_10n−5, γ₂, γ_10n−7) = 1

If v = b_2n,

gcd(f(b_2nb₁), f(b_2nb_2n−1), f(b_2nc_2n)) = gcd(γ_10n−5, γ_10n−6, γ_10n−4) = 1

If v = c_2i−1,

gcd(f(c_2i−1c_2i−2), f(c_2i−1c_2i), f(c_2i−1d_i−1), f(c_2i−1d_i))

=gcd(γ_10i−12, γ_10i−3, γ_10i−11, γ_10i) = 1, i ∈ [n] − {1}

If v = c_2i,

gcd(f(c_2ic_2i−1), f(c_2i+1c_2i), f(c_2ib_2i)) = gcd(γ_10i−3, γ_10i−2, γ_10i−4) = 1, i ∈ [n − 1]

If v = c₁,

gcd(f(c₁c₂), f(c₁c_2n), f(c₁d₁), f(c₁d_n)) = gcd(γ₇, γ_10n−2, γ₁₀, γ_10n−1) = 1

If v = c_2n,

gcd(f(c_2nc₁), f(c_2nc_2n−1), f(b_2nc_2n)) = gcd(γ_10n−2, γ_10n−3, γ_10n−4) = 1

If v = d_i,

gcd(f(d_ic_2i+1), f(d_ic_2i−1)) = gcd(γ_10i−1, γ_10i) = 1, i ∈ [n − 1]

If v = d_n,

gcd(f(d_nc₁), f(d_nc_2n−1)) = gcd(γ_10n, γ_10n−1) = 1

If v = b_2i−1,

gcd(f(b2i−1b2i),f(b2i−2b2i−1),f(b2i−1ai),f(b2i−1ai−1))=gcd(γ10i−6,γ10i−15,γ10i−8,γ10i−7)=1,i∈[n]−{1}

Hence, BLS_n is a Gaussian vertex prime graph.

□

Figure 13.1 illustrates a Gaussian vertex prime labeling of BLS₈.

Theorem 13.2

Holiday star graph HS_n is Gaussian vertex prime.◼

Proof. For the graph HS_n, V(HSn)={ui|0≤i≤2n}∪{vi|1≤i≤4n} and E(HSn)={u0u2i−1,u0u2i,u2i−1v4i−2,u2iv4i,u2i−1u2i,u0v4i−3|i∈[n]}∪{vivi+1|i∈[4n−1]}∪{v4nv1}

Here, |V(HS_n)| = 6n + 1 and |E(HS_n)| = 10n

Let us define a bijection f:E(HS_n) → [γ_10n] as follows:

Let v be an arbitrary vertex of HS_n. To prove f is Gaussian vertex prime labeling, let us consider the following cases:

If v = u₀,

gcd(f(u₀u_2i−1), f(u₀u_2i), f(u₀v_4i−3)) = gcd(γ_10i−7, γ_10i−2, γ_10i−9) = 1, i ∈ [n]

If v = u_2i−1,

gcd(f(u₀u_2i−1), f(v_4i−2u_2i−1), f(u_2iu_2i−1)) = gcd(γ_10i−7, γ_10i−6, γ_10i−1) = 1, i ∈ [n]

If v = u_2i,

gcd(f(u₀u_2i), f(v_4iu_2i), f(u_2iu_2i−1)) = gcd(γ_10i−2, γ_10i−3, γ_10i−1) = 1, i ∈ [n]

If v = v_4i−1,

gcd(f(v_4i−1v_4i), f(v_4i−2v_4i−1)) = gcd(γ_10i−4, γ_10i−5) = 1, i ∈ [n]

If v = v_4i,

gcd(f(v_4iv_4i+1), f(v_4iu_2i), f(v_4iv_4i−1)) = gcd(γ_10i, γ_10i−3, γ_10i−4) = 1, i ∈ [n − 1]

If v = v_4n,

gcd(f(v_4nv₁), f(v_4nu_2n), f(v_4nv_4n−1)) = gcd(γ_10n, γ_10n−3, γ_10n−4) = 1

If v = v₁,

gcd(f(v₁v₂), f(v₁v_4n), f(v₁u₀)) = gcd(γ₂, γ_10n, γ_10n−1) = 1

If v = v_4i−2,

gcd(f(v4i−2v4i−1),f(v4i−2v4i−3),f(v4i−2u2i−1))=gcd(γ10i−5,γ10i−8,γ10i−6)=1,i∈[n]

If v = v_4i−3,

gcd(f(v4i−3v4i−2),f(v4i−3v4i−4),f(u0v4i−3))=gcd(γ10i−8,γ10i−10,γ10i−9)=1,i∈[n]−{1}

Hence, HS_n is a Gaussian vertex prime graph.

□

Figure 13.2 illustrates a Gaussian vertex prime labeling of HS₄.

Theorem 13.3

Kusudama flower graph KF_n is Gaussian vertex prime.◼

Proof. For the graph KF_n, V(KFn)={v0}∪{wi|i∈[n]}∪{ui,vi|i∈[2n]} and E(KFn)={v0v2i,v0wi,v0u2i−1,v0u2i,wiv2i−1,wiu2i−1,wiu2i|i∈[n]}∪{vivi+1|i∈[2n−1]}∪{v2nv1}

Here, |V(KF_n)| = 5n + 1 and |E(KF_n)| = 9n

Define a bijection f:E(KF_n) → [γ_9n] as follows:

Let v ∈ V(KF_n) be an arbitrary vertex of KF_n. Now, f is proved to be a Gaussian vertex prime labeling of KF_n by considering the following cases:

If v = v₀, gcd(f(v0u2i−1),f(v0u2i),f(v0wi),f(v0v2i))=gcd(γ9i−8,γ9i−5,γ9i−6,γ9i−1)=1,i∈[n]

If v = u_2i, gcd(f(u_2iw_i), f(v₀u_2i)) = gcd(γ_9i−4, γ_9i−5) = 1, 1 ≤ i ≤ n

If v = u_2i−1, gcd(f(u_2i−1w_i), f(v₀u_2i−1)) = gcd(γ_9i−7, γ_9i−8) = 1, 1 ≤ i ≤ n

If v = v_2i−1, gcd(f(v2i−1wi),f(v2i−1v2i),f(v2i−1v2i−2))=gcd(γ9i−3,γ9i−2,γ9i−9)=1,2≤i≤n

If v = v₁, gcd(f(v₁w₁), f(v₁v₂), f(v₁v_2n)) = gcd(γ₆, γ₇, γ_9n) = 1

If v = v_2n, gcd(f(v_2nv₀), f(v_2n−1v_2n), f(v_2nv₁)) = gcd(γ_9n−1, γ_9n−2, γ_9n) = 1

If v = v_2i, gcd(f(v2iv0),f(v2iv2i−1),f(v2i+1v2i))=gcd(γ9i−1,γ9i−2,γ9i)=1,1≤i≤n−1

If v = w_i, gcd(f(u2i−1wi),f(wiv0),f(wiu2i),f(wiv2i−1))=gcd(γ9i−7,γ9i−6,γ9i−4,γ9i−3)=1, i ∈ [n]

Hence, KF_n is a Gaussian vertex prime graph.

□

Figure 13.3 illustrates a Gaussian vertex prime labeling of KF₅.

Theorem 13.4

Christmas Star graph CS_n is Gaussian vertex prime.◼

Proof. For the graph CS_n, V(CSn)={ui|0≤i≤2n}∪{vi|1≤i≤4n} and E(CSn)={u0ui|i∈[2n]}∪{u2i−1v4i−3,u2iv4i−1,u0v4i−2,u0v4i|i∈[n]}∪{vivi+1|i∈[4n−1]}∪{v4nv1}

Here, |V(CS_n)| = 6n + 1 and |E(CS_n)| = 10n

Define a bijection f:E(CS_n) → [γ_10n] as follows:

Let v be an arbitrary vertex of CS_n. We prove f is a Gaussian vertex prime labeling of CS_n by considering the following cases:

If v = u₀, gcd(f(u0u2i−1),f(u0u2i),f(u0v4i−2),f(u0v4i))=gcd(γ10i−9,γ10i−5,γ10i−6,γ10i−1)=1,i∈[n]

If v = u_2i−1, gcd(f(u₀u_2i−1), f(v_4i−3u_2i−1)) = gcd(γ_10i−9, γ_10i−8) = 1, i ∈ [n]

If v = u_2i, gcd(f(u₀u_2i), f(v_4i−1u_2i)) = gcd(γ_10i−5, γ_10i−4) = 1, i ∈ [n]

If v = v_4i−1, gcd(f(v4i−1v4i),f(v4i−1u2i),f(v4i−2v4i−1))=gcd(γ10i−2,γ10i−4,γ10i−3)=1,i∈[n]

If v = v_4i, gcd(f(v_4iv_4i+1), f(v_4iu₀), f(v_4iv_4i−1)) = gcd(γ_10i, γ_10i−1, γ_10i−2) = 1, i ∈ [n − 1]

If v = v_4n, gcd(f(v4nv1),f(v4nu0),f(v4nv4n−1))=gcd(γ10n,γ10n−1,γ10n−2)=1

If v = v₁, gcd(f(v₁v₂), f(v₁v_4n), f(v₁u₁)) = gcd(γ₃, γ_10n, γ₂) = 1

If v = v_4i−2, gcd(f(v4i−2v4i−1),f(v4i−2v4i−3),f(v4i−2u0))=gcd(γ10i−3,γ10i−7,γ10i−6)=1,i∈[n]

If v = v_4i−3, gcd(f(v4i−3v4i−2),f(v4i−3v4i−4),f(u2i−1v4i−3))=gcd(γ10i−7,γ10i−10,γ10i−8)=1,i∈[n]−{1}

Hence, CS_n is a Gaussian vertex prime graph.

□

Figure 13.4 illustrates a Gaussian vertex prime labeling of CS₄.

Theorem 13.5

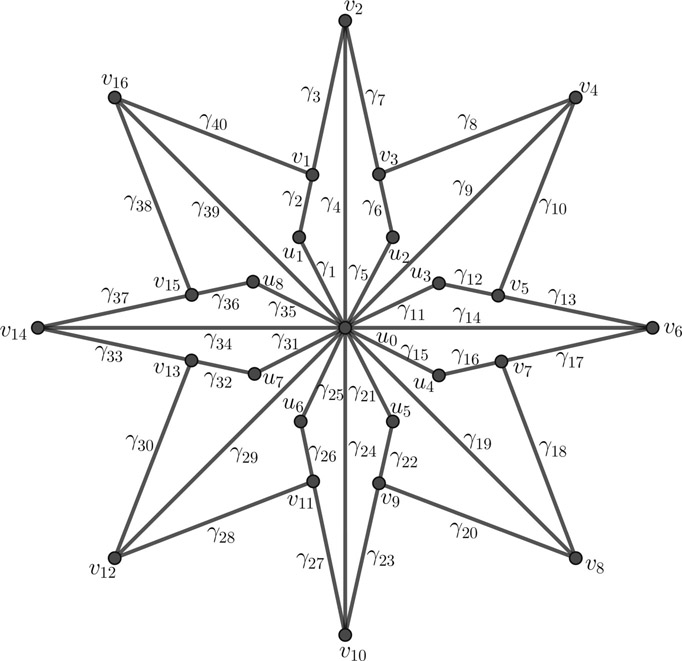
Braided star graph BRS_n is Gaussian vertex prime.◼

Proof. For the graph BRS_n, V(BRSn)={a0}∪{ai,di|i∈[n]}∪{bi,ci|i∈[2n]} and E(BRSn)={a0ai,aib2i−1,b2ic2i,c2i−1di|i∈[n]}∪{bibi+1,cici+1|i∈[2n−1]}∪{ana1,c2nc1,b2nb1,dnc1}∪{aiai+1,dic2i+1|i∈[n−1]}

Here, |V(BRS_n)| = 6n + 1 and |E(BRS_n)| = 10n

Define a bijection f:E(BRS_n) → [γ_10n] as follows:

Let v be an arbitrary vertex of BRS_n. We prove f is a Gaussian vertex prime labeling of BRS_n by considering the following cases:

If v = a_n, gcd(f(ana0),f(ana1),f(anb2n−1),f(anan−1))=gcd(γ10n−9,γ10n−8,γ10n−7,γ10n−18)=1

If v = a₀, gcd(f(a₀a₁), f(a₀a₂), …, f(a₀a_n)) = gcd(γ₁, γ₁₁, …, γ_10n−9) = 1

If v = a₁, gcd(f(a1a0),f(a2a1),f(a1b1),f(ana1))=gcd(γ1,γ2,γ3,γ10n−8)=1

If v = b_2i, gcd(f(b2ib2i+1),f(b2ib2i−1),f(b2ic2i))=gcd(γ10i−5,γ10i−6,γ10i−4)=1,i∈[n−1]

If v = b_2n, gcd(f(b2nb1),f(b2nb2n−1),f(b2nc2n))=gcd(γ10n−5,γ10n−6,γ10n−4)=1

If v = b₁, gcd(f(b₁b₂), f(b₁b_2n), f(a₁b₁)) = gcd(γ₄, γ_10n−5, γ₃) = 1

If v = c_2i, gcd(f(c2ic2i−1),f(c2i+1c2i),f(c2ib2i))=gcd(γ10i−3,γ10i−2,γ10i−4)=1,i∈[n−1]

If v = c₁, gcd(f(c1c2),f(c1c2n),f(c1d1),f(c1dn))=gcd(γ7,γ10n−2,γ10,γ10n−1)=1

If v = c_2n, gcd(f(c2nc1),f(c2nc2n−1),f(b2nc2n))=gcd(γ10n−2,γ10n−3,γ10n−4)=1

If v = d_i, gcd(f(d_ic_2i+1), f(d_ic_2i−1)) = gcd(γ_10i−1, γ_10i) = 1, i ∈ [n − 1]

If v = d_n, gcd(f(d_nc₁), f(d_nc_2n−1)) = gcd(γ_10n, γ_10n−1) = 1

If v = a_i, gcd(f(aia0),f(aiai+1),f(aib2i−1),f(aiai−1))=gcd(γ10i−9,γ10i−8,γ10i−7,γ10i−18)=1, i ∈ [n − 1] − {1}

If v = b_2i−1, gcd(f(b2i−1b2i),f(b2i−2b2i−1),f(b2i−1ai))=gcd(γ10i−6,γ10i−15,γ10i−7)=1,i∈[n]−{1}

If v = c_2i−1, gcd(f(c_2i−1c_2i−2), f(c_2i−1c_2i), f(c_2i−1d_i−1), f(c_2i−1d_i)) = gcd(γ_10i−12, γ_10i−3, γ_10i−11, γ_10i) = 1, i ∈ [n] − {1}

□

Hence, BRS_n is a Gaussian vertex prime graph.

Figure 13.5 illustrates a Gaussian vertex prime labeling of BRS₈.

Theorem 13.6

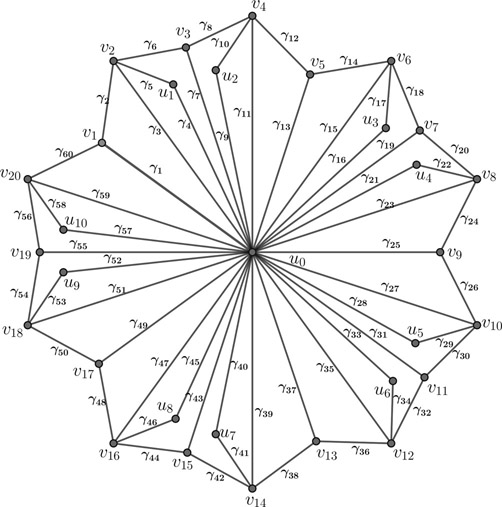
Cherry blossom graph CB_n is Gaussian vertex prime.◼

Proof. For the graph CB_n, V(CBn)={u0}∪{vi|i∈[4n]}∪{ui|i∈[2n]} and E(CBn)={uiv2i,u0ui|i∈[2n]}∪{vivi+1|i∈[4n−1]}∪{u0vi|i∈[4n]}∪{v4nv1}