12.1Introduction and Definitions

In this chapter, we consider the simple, finite, connected and undirected graph G = (V(G), E(G)) with V(G) as vertex set and E(G) as edge set. For various notations and terminology of graph theory, we follow Gross and Yellen [3] and for some results of number theory, we follow Burton [2].

Let G be a graph with n vertices. A bijective function f:V(G)→{1,2,3,…,n} is said to be a neighborhood-prime labeling if for every vertex u in V(G) with deg(u) > 1, gcd {f(p)|p∈N(u)}=1, where N(u) = {w∈V(G)|uw∈E(G)}. A graph which admits neighborhood-prime labeling is called a neighborhood-prime graph.

The notion of neighborhood-prime labeling was introduced by Patel and Shrimali [4]. In [5] they proved the union of some graphs are neighborhood-prime graphs. They also proved that the product of some graphs are neighborhood-prime [6]. For a further list of results regarding neighborhood-prime graphs the reader may refer to [1].

In a neighborhood-prime labeling, edges are not considered. Kumar and Varkey extended the condition on edges and they defined total neighborhood prime labeling [7].

Definition (Total neighborhood prime labeling). Let G be a graph. For u ∈ V(G),

A bijective function f:V(G)∪E(G)→ {1,2,3,…,|V(G)∪E(G)|} is said to be a total neighborhood prime labeling, if for each vertex u with degree greater than 1, gcd {f(w)|w∈NV(u)}=1 and gcd{f(e)|e∈NE(u)}=1. A graph which admits total neighborhood prime labeling is called a total neighborhood prime graph.

Kumar and Varkey proved that path, cycle C_4k and comb graphs admit total neighborhood prime labeling [7]. Shrimali and Pandya proved comb, disjoint union of paths, disjoint union of sunlet graphs, disjoint union of wheel graphs, graph obtained by one copy of path P_n and n copies of K_1,m and joining i^th vertex of P_n with an edge to fixed vertex in the i^th copy of K_1,m, corona product of cycle with m copy of K₁ and subdivision of bistar are total neighborhood prime graphs [8].

Definition (Armed crown). Armed crown is the graph obtained by attaching a path P₂ at each vertex of cycle C_n. It is denoted by ACn.

Definition (Join graph) Let G₁ = (V (G₁), E(G₁)) and G₂ = (V (G₂), E(G₂)) be two graphs with no vertex in common. The join graph of G₁ and G₂ denoted by G₁ + G₂ is the graph with vertex set V(G1+G2)=V(G1)⋃V(G2) and edge set E(G1+G2)=E(G1)⋃E(G2)⋃{uv:u∈V(G1),v∈V(G2)}.

12.2Main Results

Theorem 12.1

AC_n + K₁ is a total neighborhood prime graph.◼

Proof. Let G = AC_n + K₁. Let u1,u2,…,un be the vertices of C_n , u_i,1 and u_i,2 be the vertices of i^th copy of path P₂ for each i in AC_n and u be the vertex corresponding to K₁. By the definition of join graph, u is adjacent to each vertex of a graph AC_n, u_i,1 is adjacent to u_i,2 and u_i for i=1,2,…,n. Let d_i = u_i u_i+1(value of i is taken modulo n), e_i,j = u u_i,j and e_i = u u_i for i=1,2,…,n and j = 1, 2 and g_i,1 = u_i u_i,1, g_i,2 = u_i,1 u_i,2 for i=1,2,…,n.

So, vertex set V(G)={u,ui,ui,j/i=1,2,…,n and j = 1, 2} and edge set E(G)={ei,di/i=1,2,…,n}∪{ei,j,gi,j/i=1,2,…,n and j = 1, 2}

We define f:V(G)∪E(G)⟶{1,2,3,…,|V(G)∪E(G)|} as follows.

f(u) = 1,

f(u_i) = 8i − 1, 1 ≤ i ≤ n

f(ui,j)={8i,j=18i+1,j=2.,1≤i≤n

f(e_i) = 8(i − 1) + 4, 1 ≤ i ≤ n

f(ei,j)={8(i−1)+6,j=18(i−1)+3,j=2.,1≤i≤n

f(gi,j)={8(i−1)+5,j=18(i−1)+2,j=2.,1≤i≤n

f(d_i) = 8n + 1 + i, 1 ≤ i ≤ n

In order to prove f is a total neighborhood prime labeling, we have to show that both the conditions are satisfied by f. Let w be an arbitrary vertex in V(G). For w ≠ u, since f(u) = 1 and u ∈ N_V(w), gcd {f(p)/p ∈ N_V(w)} = 1 and for w = u, {f(p)/p ∈ N_V(w)} contains at least two consecutive numbers, so gcd {f(p)/p ∈ N_V(w)} = 1. For any vertex w, {f(e)/e ∈ N_E(w)} contains at least two consecutive numbers or consecutive odd numbers, so gcd {f(e)/e ∈ N_E(w)} = 1. Therefore, f is a total neighborhood prime labeling. Hence, G is a total neighborhood prime graph.□

Illustration 12.2.1. Total neighborhood prime labeling of AC₄ + K₁ is shown in Figure 12.1.

Theorem 12.2

(⋃i=1pCni)+K1 is a total neighborhood prime graph.◼

Proof. Let G=(⋃i=1pCni)+K1. Let ui,1,ui,2,ui,3,…,ui,ni be the vertices of i^th cycle Cni where 1 ≤ i ≤ p and u be the vertex corresponding to K₁. By the definition of join graph, u is adjacent to each vertex of ⋃i=1pCni. Let e_i,j = u_i,j u_i,j+1 and d_i,j = u u_i,j for 1 ≤ i ≤ p, 1 ≤ j ≤ n_i where the value of j is taken modulo n_i. Vertex set V(G)={ui,j,u/i=1,2,…,p and j=1,2,…,ni} and edge set E(G)={ei,j,di,j/i=1,2,…,p and j=1,2,…,ni}.

Now we define the function f:V(G)∪E(G)⟶{1,2,3,…,|V(G)∪E(G)|} as follows.

f(u) = 1,

f(ui,j)={2n1+1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+2ni+j,2≤i≤p,1≤j≤ni

f(ei,j)={1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+j,2≤i≤p,1≤j≤ni

f(di,j)={n1+j+1,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+ni+j,2≤i≤p,1≤j≤ni

We will show that both the conditions for total neighborhood prime labeling are satisfied by f. Let w be an arbitrary vertex in V(G). For w ≠ u, gcd {f(p)/p ∈ N_V(w)} = 1 because f(u) = 1 and u ∈ N_V(w). For w = u, {f(p)/p ∈ N_V(w)} contains at least two consecutive numbers, so gcd {f(p)/p ∈ N_V(w)} = 1. For any vertex w, {f(e)/e ∈ N_E(w)} contains at least two consecutive numbers or consecutive odd numbers, so gcd {f(e)/e ∈ N_E(w)} = 1. Therefore, f is a total neighborhood prime labeling and G is a total neighborhood prime graph.□

Illustration 12.2.2. Total neighborhood prime labeling of (C4⋃C5⋃C6)+K1 is shown in Figure 12.2.

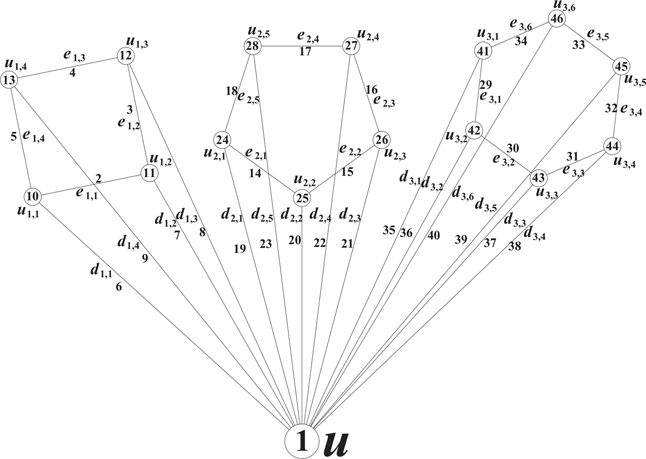
Theorem 12.3

[Pn⋃(⋃i=1pCni)]+K1 is a total neighborhood prime graph.◼

Proof. Let G=[Pn⋃(⋃i=1pCni)]+K1. Let v1,v2,…,vn be the consecutive vertices of path P_n and ui,1,ui,2,ui,3,…,ui,ni be the vertices of i^th cycle Cni where 1 ≤ i ≤ p. Let u be the vertex corresponding to K₁. So by the definition of join graph, u is adjacent to each vertex of Pn⋃(⋃i=1pCni). Let e_i,j = u_i,j u_i,j+1 and d_i,j = u u_i,j for 1 ≤ i ≤ p, 1 ≤ j ≤ n_i where value of j is taken modulo n_i. Let g_i = v_iv_i+1 for i=1,2,…,n−1 and g_i′ = uv_i for i=1,2,…,n.

Vertex set V(G)={ui,j,u/i=1,2,…,p and j=1,2,…,ni}⋃{v1,v2,…,vn} and edge set E(G)={ei,j,di,j/i=1,2,…,p and j=1,2,…,ni}⋃{g1,g2,… ,gn−1}⋃{g1′,g2′,…,gn′} .

Now we define the function f:V(G)∪E(G)⟶{1,2,3,…,|V(G)∪E(G)|} as follows.

f(u) = 1,

f(ui,j)={2n1+1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+2ni+j,2≤i≤p,1≤j≤ni

f(ei,j)={1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+j,2≤i≤p,1≤j≤ni

f(di,j)={n1+j+1,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+ni+j,2≤i≤p,1≤j≤ni

f(vi)=3(n1+n2+,…,+np)+2n+i, 1 ≤ i ≤ n,

f(gi)=3(n1+n2+,…,+np)+2i+1, 1 ≤ i ≤ n − 1,

f(gi′)=3(n1+n2+,…,+np)+2i, 1 ≤ i ≤ n.

Let w be an arbitrary vertex in V(G). For w ≠ u, since f(u) = 1 and u ∈ N_V(w), gcd {f(p)/p ∈ N_V(w)} = 1 and for w = u, gcd {f(p)/p ∈ N_V(w)} = 1 because {f(p)/p ∈ N_V(w)} contains at least two consecutive numbers. For any vertex w, gcd {f(e)/e ∈ N_E(w)} = 1 because {f(e)/e ∈ N_E(w)} contains at least two consecutive numbers or consecutive odd numbers. Since both the conditions for total neighborhood prime labeling are satisfied, f is a total neighborhood prime labeling and hence G is a total neighborhood prime graph.□

Illustration 12.2.3. Total neighborhood prime labeling of (P9⋃C3⋃C5⋃C6) +K₁ is shown in Figure 12.3.

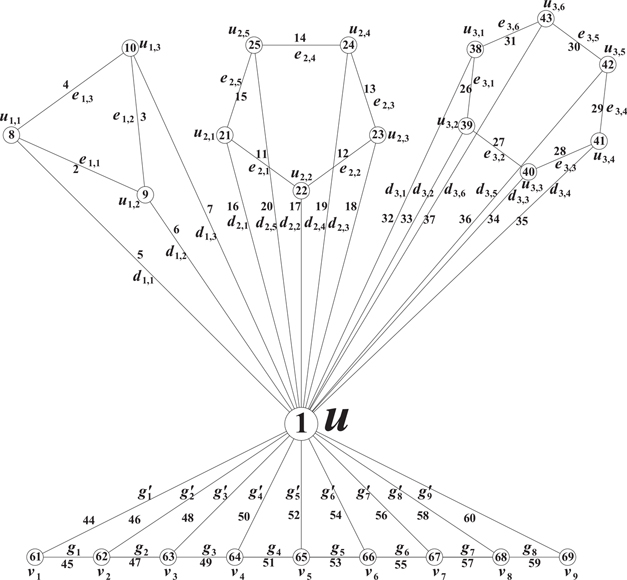
Theorem 12.4

[K1,n⋃(⋃i=1pCni)] +K₁ is a total neighborhood prime graph.◼

Proof. Let G=[K1,n⋃(⋃i=1pCni)]+K1. Let v,v1,v2,…,vn be the vertices of star graph K_1,n where v is the apex vertex. Let ui,1,ui,2,ui,3,…,ui,ni be the vertices of i^th cycle Cni where 1 ≤ i ≤ p. Let u be the vertex corresponding to K₁. So by the definition of join graph, u is adjacent to each vertex of K1,n⋃(⋃i=1pCni). Let e_i,j = u_i,j u_i,j+1 and d_i,j = u u_i,j for 1 ≤ i ≤ p, 1 ≤ j ≤ n_i where value of j is modulo n_i. Let g_i = uv_i, h_i = vv_i for i=1,2,…,n and e = uv.

Vertex set V(G)={ui,j/i=1,2,…,p and j=1,2,…,ni}⋃{v1,v2,…,vn} ⋃{u,v} and edge set E(G)={ei,j,di,j/i=1,2,…,p and j=1,2,…,ni}⋃{g1, g2,…,gn} ⋃{h1,h2,…,hn}⋃{x,x1,x2}.

Now we define the function f:V(G)∪E(G)⟶{1,2,3,…,|V(G)∪E(G)|} as follows.

f(u) = 1,

f(ui,j)={2n1+1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+2ni+j,2≤i≤p,1≤j≤ni

f(ei,j)={1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+j,2≤i≤p,1≤j≤ni

f(di,j)={n1+j+1,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+ni+j,2≤i≤p,1≤j≤ni

f(vi)=3(n1+n2+,…,+np)+2n+1+i, 1 ≤ i ≤ n,

f(gi)=3(n1+n2+,…,+np)+2i+1, 1 ≤ i ≤ n,

f(hi)=3(n1+n2+,…,+np)+2i, 1 ≤ i ≤ n,

f(e)=3(n1+n2+,…,+np)+3n+3,

f(v)=3(n1+n2+,…,+np)+3n+2.

Let w be an arbitrary vertex in V(G). For w ≠ u, gcd {f(p)/p ∈ N_V(w)} = 1 because f(u) = 1 and u ∈ N_V(w). For w = u, since {f(p)/p ∈ N_V(w)} contains at least two consecutive numbers, gcd {f(p)/p ∈ N_V(w)} = 1 . For any vertex w, {f(e)/e ∈ N_E(w)} contains at least two consecutive numbers or consecutive odd numbers, so gcd {f(e)/e ∈ N_E(w)} = 1. Therefore, f is a total neighborhood prime labeling. Thus, G is a total neighborhood prime graph.

Illustration 12.2.4. Total neighborhood prime labeling of (K1,8⋃C4⋃C5 ⋃C6)+K1 is shown in Figure 12.4.

Theorem 12.5

[Bm,n⋃(⋃i=1pCni)]+K1 is a total neighborhood prime graph.□

Proof. Let G=[Bm,n⋃(⋃i=1pCni)]+K1. Let v1,v2,v1,1,v1,2,…,v1,m,v2,1,v2,2, …,v2,n be the vertices of bistar graph B_m,n where v1,1,v1,2,…,v1,m are adjacent to v₁ and v2,1,v2,2,…,v2,n are adjacent to v₂. Let ui,1,ui,2,ui,3,…,ui,ni be the vertices of i^th cycle Cni where 1 ≤ i ≤ p. Let u be the vertex corresponding to K₁. So by the definition of join graph, u is adjacent to each vertex of Bm,n⋃(⋃i=1pCni). Let e_i,j = u_i,j u_i,j+1 and d_i,j = u u_i,j for 1 ≤ i ≤ p, 1 ≤ j ≤ n_i where the value of j is taken modulo n_i. Let g_i,j = v_iv_i,j and h_i,j = uv_i,j for i = 1, j=1,2,…,m and for i = 2, j=1,2,…,n. let t = v₁ v₂ and t_i = uv_i for i = 1, 2.

Vertex set V(G)={ui,j/i=1,2,…,p and j=1,2,…,ni}⋃{v1,1,v1,2,…,v1,m} ⋃{v2,1,v2,2,…,v2,n} ⋃{u,v1,v2} and edge set E(G)={ei,j,di,j/i=1,2,…,p and j=1,2,…,ni}⋃{g1,1,g1,2,…,g1,m,g2,1,g2,2,…,g2,n}⋃{h1,1,h1,2,…,h1,m,h2,1,h2,2,…,h2,n}.

Now we define the function f:V(G)∪E(G)⟶{1,2,3,…,|V(G)∪E(G)|} as follows.

f(u) = 1,

f(ui,j)={2n1+1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+2ni+j,2≤i≤p,1≤j≤ni

f(ei,j)={1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+j,2≤i≤p,1≤j≤ni

f(di,j)={n1+j+1,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+ni+j,2≤i≤p,1≤j≤ni

f(vi)=3(n1+n2+,…,+np)+3(m+n)+4+i, i = 1, 2,

f(vi,j)={3(n1+n2+,…,+np)+2(m+n)+4+j,i=1,1≤j≤m3(n1+n2+,…,+np)+3m+2n+4+j,i=2,1≤j≤n

f(gi,j)={3(n1+n2+,…,+np)+2j+1,i=1,1≤j≤m3(n1+n2+,…,+np)+2m+2j+1,i=2,1≤j≤n

f(hi,j)={3(n1+n2+,…,+np)+2j,i=1,1≤j≤m3(n1+n2+,…,+np)+2m+2j,i=2,1≤j≤n

f(ti)=3(n1+n2+,…,+np)+2(m+n)+2+i, i = 1, 2,

f(t)=3(n1+n2+,…,+np)+2(m+n)+2.

Let w be an arbitrary vertex in V(G). For w ≠ u, since f(u) = 1 and u ∈ N_V(w), gcd {f(p)/p ∈ N_V(w)} = 1 and for w = u, gcd {f(p)/p ∈ N_V(w)} = 1 because {f(p)/p ∈ N_V(w)} contains at least two consecutive numbers. For any vertex w, gcd {f(e)/e ∈ N_E(w)} = 1 because {f(e)/e ∈ N_E(w)} contains at least two consecutive numbers or consecutive odd numbers. Since both the conditions for total neighborhood prime labeling are satisfied, f is a total neighborhood prime labeling and G is a total neighborhood prime graph.□

Illustration 12.2.5. Total neighborhood prime labeling of (B3,3⋃C3⋃C5 ⋃C6)+K1 is shown in Figure 12.5.

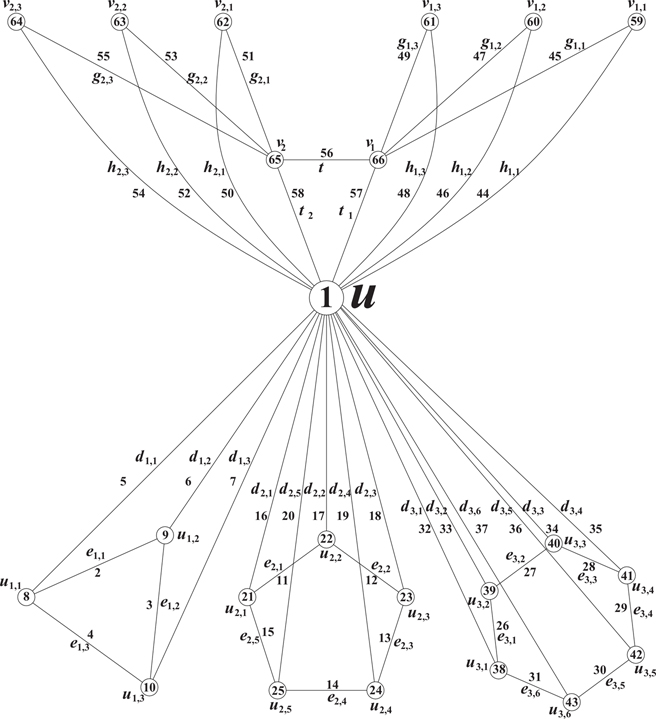
Theorem 12.6

[(Pn⊙K1)⋃(⋃i=1pCni)]+K1 is a total neighborhood prime graph.◼

Proof. Let G=[(Pn⊙K1)⋃i=1pCni)]+K1. Let v1,j,v2,j,…,vn,j be the vertices of comb graph (Pn⊙K1) for j = 1, 2. v_i,1 is adjacent to v_i−1,1 and v_i+1,1 for i=2,3,…,n−1. v_i,1 is also adjacent v_i,2 for i=1,2,…,n. Let ui,1,ui,2,ui,3,…,ui,ni be the vertices of i^th cycle Cni where 1 ≤ i ≤ p. Let u be the vertex corresponding to K₁. So by the definition of join graph, u is adjacent to each vertex of [(Pn⊙K1)⋃i=1pCni)]. Let e_i,j = u_i,j u_i,j+1 and d_i,j = u u_i,j for 1 ≤ i ≤ p, 1 ≤ j ≤ n_i where the value of j is taken modulo n_i. Let g_i = v_i,1v_i+1,1 for i=1,2,…,n−1, g_i′ = v_i,1v_i,2 for i=1,2,…,n and h_i,j = uv_i,j for i=1,2,…,n and j = 1, 2.

Vertex set V(G)={ui,j/i=1,2,…,p and j=1,2,…,ni}⋃{vi,1,vi,2,…,vi,n/i=1,2} and edge set E(G)={ei,j,di,j/i=1,2,…,p and j=1,2,…,ni}⋃{g1,g2,… ,gn−1}⋃{g1′,g2′,…,gn′}⋃{hi,1,hi,2,…,hi,n/i=1,2}.

Now we define the function f:V(G)∪E(G)⟶{1,2,3,…,|V(G)∪E(G)|} as follows.

f(u) = 1,

f(ui,j)={2n1+1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+2ni+j,2≤i≤p,1≤j≤ni

f(ei,j)={1+j,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+j,2≤i≤p,1≤j≤ni

f(di,j)={n1+j+1,i=1,1≤j≤n11+3(n1+n2+,…,+ni−1)+ni+j,2≤i≤p,1≤j≤ni

f(vi,j)={3(n1+n2+,…,+np)+4n+i,1≤i≤n,j=13(n1+n2+,…,+np)+5n+i,1≤i≤n,j=2

f(hi,j)={3(n1+n2+,…,+np)+2n+2i,1≤i≤n,j=13(n1+n2+,…,+np)+2i,1≤i≤n,j=2

f(gi)=3(n1+n2+,…,+np)+2n+2i+1, i=1,2,…,n−1,

f(gi′)=3(n1+n2+,…,+np)+2i+1, i=1,2,…,n

Let w be an arbitrary vertex in V(G). For w ≠ u, gcd {f(p)/p ∈ N_V(w)} = 1 because f(u) = 1 and u ∈ N_V(w). For w = u, since {f(p)/p ∈ N_V(w)} contains at least two consecutive numbers, gcd {f(p)/p ∈ N_V(w)} = 1 . For any vertex w, {f(e)/e ∈ N_E(w)} contains at least two consecutive numbers or consecutive odd numbers, so gcd {f(e)/e ∈ N_E(w)} = 1. Since both the conditions for total neighborhood prime labeling are satisfied, f is a total neighborhood prime labeling and G is a total neighborhood prime graph.□

Illustration 12.2.6. Total neighborhood prime labeling of [(P8⊙K1)⋃C3 ⋃C4⋃C6]+K1 is shown in Figure 12.6.

References

1.J. A. Gallian. A dynamic survey of graph labeling. The Electronic Journal of Combinatorics, #DS6, 2018.

2.D. M. Burton. Elementary Number Theory. Seventh Edition, McGraw-Hill Publisher, 2010.

3.J. Gross and J. Yellen. Graph Theory and its Applications. CRC Press, 2005.

4.S. K. Patel and N. P. Shrimali. Neighborhood-prime labeling. International Journal of Mathematics and Soft Computing, 5(2): 135-143, 2015.

5.S. K. Patel and N. P. Shrimali. Neighborhood-prime labeling of some union graphs. International Journal of Mathematics and Soft Computing, 6(1): 39-47, 2016.

6.S. K. Patel and N. P. Shrimali. Neighborhood-prime labeling of some product graphs. Algebra and Discrete Mathematics, 25(1): 118-129, 2018.

7.Rajesh Kumar and Mathew Varkey. A note on Total neighborhood prime labeling. International Journal of Pure and Applied Mathematics, 118(4): 1007-1013, 2018.

8.N. P. Shrimali and Parul B. Pandya. Total neighborhood prime labeling of some graphs. International Journal of Scientific Research in Mathematical and Statistical Sciences, 5(6): 157-163, 2018.