Chapter 16: Distance Magic and Distance Antimagic Labeling of Some Product Graphs

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

N P Shrimali

Department of Mathematics,
Gujarat University,
Ahmedabad,
Gujarat (INDIA)
E-mail: [email protected]

Y M Parmar

Department of Mathematics,
Gujarat University,
Ahmedabad, Gujarat (INDIA)
E-mail: [email protected]

Let G = (V, E) be a graph of order n. Let f:V(G) → {1, 2, …, n} be a bijection. For any vertex q ∈ V(G), the sum $\sum_{p \in N (q)} f (p)$ is called the weight of the vertex q and is denoted by w(q). If there exists a positive integer γ such that w(q) = γ, for every q ∈ V(G), then f is called a distance magic labeling. The constant γ is called the magic constant for f. A graph which admits a distance magic labeling is called a distance magic graph. If w(q) ≠ w(r) for any two distinct vertices q and r, then f is called a distance antimagic labeling. A graph which admits a distance antimagic labeling is called a distance antimagic graph. In this chapter, we discuss the existence of distance magic labeling and distance antimagic labeling for $C_{3}^{t} ◻ C_{4}$ , $C_{3}^{t} \times C_{4}$ , $C_{3}^{t} ⊠ C_{4}$ and $C_{4} ⊙ C_{3}^{t}$ .

16.1Introduction

Here, we consider that all graphs G with vertex set V(G) and edge set E(G) are finite and simple. We adopt Gross and Yellen [5] for various graphs and its theoretic notations and for number theoretical results, we follow Burton [3]. For acquiring the latest update, we follow a dynamic survey on graph labeling by Gallian [4].

A distance magic labeling distance magic labeling of a graph G of order n is a bijection f:V(G) → {1, 2, …, n} such that $\sum_{p \in N (q)} f (p) = γ$ , for all q ∈ V(G), where N(q) is the set of all vertices of V(G) which are adjacent to q. The constant γ is called the magic constant of the distance magic labeling for f. A graph which admits a distance magic labeling is called a distance magic graph. For any vertex q ∈ V(G), the neighbor sum $\sum_{p \in N (q)} f (p)$ is called the weight of the vertex q and is denoted by w(q).

The concept of distance magic labeling was introduced and studied by many researchers with different terminologies. For example, the term sigma labeling is used by Vilfred [10], the term 1-vertex magic labeling [1-VML] is used by Miller et al. [7], the term neighborhood magic labeling is used by B.D.Acharya et al. [1] and the term distance magic labeling is used by Sugeng et al. [9].

The following lemmas are proved by Miller et al. [7].

Lemma 16.1

[7] A necessary condition for the existance of a distance magic vertex labeling f of a graph G is

γ v = \sum_{p \in V (G)} d (p) f (p)

where d(p) is the degree of vertex p and v is the number of vertices of G.◼

Lemma 16.2

[7] If G contains two vertices p and q such that $| N (p) \cap N (q) | = d (p) - 1 = d (q) - 1$ , then G has no distance magic labeling.◼

A distance antimagic labeling of a graph G of order n is a bijection f:V(G) → {1, 2, …, n} such that $\sum_{p \in N (q)} f (p) = w (q)$ for all q ∈ V(G), where N(q) is the set of all vertices of V(G) which are adjacent to q and w(p) ≠ w(q) for every pair of vertices p, q ∈ V(G). A graph which admits a distance antimagic labeling is called a distance antimagic graph.

A distance antimagic labeling was introduced by Simanjuntak and Wijaya [8] in 2013. They proved the following Lemma:

Lemma 16.3

[8] If a graph contains two vertices with the same neighborhood then it is not distance antimagic.◼

They also proved that cycles, suns, wheel W_n for n ≠ 5, fan F_n for n ≠ 4, friendship graphs f_n are distance antimagic graphs and multipartite graphs are not distance antimagic graphs.

Definition. [6] A Cartesian product, denoted by $G ◻ H$ is a graph with vertex set V(G) × V(H). Vertices (p, q) and (p′, q′) in $G ◻ H$ are adjacent if and only if p = p′ and q is adjacent to q′ in H or q = q′ and p is adjacent to p′ in G.

Definition. [6] A Direct product, denoted by G × H is a graph with vertex set V(G) × V(H). Vertices (p, q) and (p′, q′) in G × H are adjacent if and only if p is adjacent to p′ in G and q is adjacent to q′ in H.

Definition. [6] A strong product, denoted by $G ⊠ H$ is a graph with vertex set V(G) × V(H). Vertices (p, q) and (p′, q′) in $G ⊠ H$ are adjacent if and only if p = p′ and q is adjacent to q′ in H or q = q′ and p is adjacent to p′ in G or p is adjacent to p′ in G and q is adjacent to q′ in H.

Definition. A corona product $G ⊙ H$ of two graphs G and H is obtained by taking one copy of G and |V (G)| copies of H; and by joining each vertex of the i-th copy of H to the i-th vertex of G, where 1 ≤ i ≤ |V (G)|.

M. Anholcer and S. Cichacz [2] have already proved that $C_{3}^{t} \circ C_{4}$ is not distance magic. In this chapter, we apply some more products between $C_{3}^{t}$ and C₄. We investigate the existence of distance magic labeling and distance antimagic labeling of $C_{3}^{t} ◻ C_{4}$ , $C_{3}^{t} \times C_{4}$ , $C_{3}^{t} ⊠ C_{4}$ and $C_{4} ⊙ C_{3}^{t}$ graphs.

Throughout this chapter, friendship graph $C_{3}^{t}$ consists of t − triangles with a common vertex r and vertices p_k, q_k for k = 1, 2, …, t. i.e. p_k, q_k are the vertices of the k^th copy of cycle C₃. Let C₄ = c₀c₁c₂c₃c₀ be a cycle. Here, $G = C_{3}^{t} ◻ C_{4}, C_{3}^{t} ⊠ C_{4}$ and $C_{3}^{t} \times C_{4}$ are graphs with vertex set $V (G) = {p_{k}^{j}, q_{k}^{j}, r^{j} / 1 \leq k \leq t, 0 \leq j \leq 3}$ , where $p_{k}^{j} = (p_{k}, c_{j}), q_{k}^{j} = (q_{k}, c_{j}), r^{j} = (r, c_{j})$ .

16.2Cartesian Product of $C_{3}^{t}$ and C₄

Theorem 16.1

The graph $C_{3}^{t} ◻ C_{4}$ is not distance magic.◼

Proof. Suppose that the graph $G = C_{3}^{t} ◻ C_{4}$ is a distance magic graph under distance magic labeling f. So weights of each vertex are equal.

Now,

\begin{aligned} w (r^{0}) = \sum_{k = 1}^{t} (f (p_{k}^{0}) + f (q_{k}^{0})) + f (r^{1}) + f (r^{3}) \\ and & w (r^{2}) = \sum_{k = 1}^{t} (f (p_{k}^{2}) + f (q_{k}^{2})) + f (r^{1}) + f (r^{3}) \end{aligned}

Since, w(r⁰) = w(r²),

$\sum_{k = 1}^{t} (f (p_{k}^{0}) + f (q_{k}^{0})) = \sum_{k = 1}^{t} (f (p_{k}^{2}) + f (q_{k}^{2}))$	(16.1)

Now, for 1 ≤ k ≤ t

\begin{aligned} w (p_{k}^{0}) = f (q_{k}^{0}) + f (p_{k}^{1}) + f (p_{k}^{3}) + f (r^{0}) \\ and & w (p_{k}^{2}) = f (q_{k}^{2}) + f (p_{k}^{1}) + f (p_{k}^{3}) + f (r^{2}) \end{aligned}

Since, $w (p_{k}^{0}) = w (p_{k}^{2})$ ,

$f (q_{k}^{0}) + f (r^{0}) = f (q_{k}^{2}) + f (r^{2}), \forall k$	(16.2)

Analogously, we can derive the following equation,

$f (p_{k}^{0}) + f (r^{0}) = f (p_{k}^{2}) + f (r^{2}), \forall k$	(16.3)

Adding the above 2t equations, we get

$\sum_{k = 1}^{t} (f (p_{k}^{0}) + f (q_{k}^{0})) + 2 t f (r^{0}) = \sum_{k = 1}^{t} (f (p_{k}^{2}) + f (q_{k}^{2})) + 2 t f (r^{2})$	(16.4)

From, (16.1) and (16.4), f(r⁰) = f(r²), which is not possible.

Hence, the graph $C_{3}^{t} ◻ C_{4}$ is not a distance magic graph.□

Theorem 16.2

The graph ${C_{3}}^{t} ◻ C_{4}$ is distance antimagic.◼

Proof. We define a vertex labeling f:V(G) → {1, 2, …, |V(G)|} as follows:

For k = 1, 2, …, t,

\begin{aligned} f (p_{k}^{0}) = 8 k - 7; \\ f (p_{k}^{1}) = 8 k - 2; \\ f (p_{k}^{2}) = 8 k - 6; \\ f (p_{k}^{3}) = 8 k - 3; \\ f (q_{k}^{0}) = 8 k - 5; \\ f (q_{k}^{1}) = 8 k; \\ f (q_{k}^{2}) = 8 k - 4; \\ f (r^{0}) = 8 t + 2; \\ f (r^{1}) = 8 t + 1; \\ f (r^{2}) = 8 t + 4; \\ f (r^{3}) = 8 t + 3 \end{aligned}

Under the above labeling, weights for each vertex are as follows:

For 1 ≤ k ≤ t,

\begin{aligned} w (p_{k}^{0}) = 8 t + 24 k - 8; \\ w (p_{k}^{1}) = 8 t + 24 k - 12; \\ w (p_{k}^{2}) = 8 t + 24 k - 5; \\ w (p_{k}^{3}) = 8 t + 24 k - 11; \\ w (q_{k}^{0}) = 8 t + 24 k - 6; \\ w (q_{k}^{1}) = 8 t + 24 k - 10; \\ w (q_{k}^{2}) = 8 t + 24 k - 3; \\ w (q_{k}^{3}) = 8 t + 24 k - 9; \\ w (r^{0}) = 8 t^{2} + 12 t + 4; \\ w (r^{1}) = 8 t^{2} + 22 t + 6; \\ w (r^{2}) = 8 t^{2} + 14 t + 4; \\ w (r^{3}) = 8 t^{2} + 20 t + 6 \end{aligned}

Since weights of each vertex are distinct, ${C_{3}}^{t} ◻ C_{4}$ is a distance antimagic graph.□

Illustration 16.2.1. The distance antimagic labeling for $C_{3}^{2} ◻ C_{4}$ is given in Figure 16.1.

Figure 16.1: Distance antimagic labeling for $C_{3}^{2} ◻ C_{4}$

16.3Direct Product of $C_{3}^{t}$ and C₄

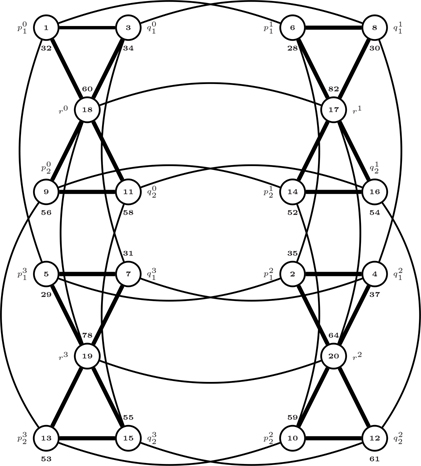
Theorem 16.3

The graph ${C_{3}}^{t} \times C_{4}$ is not distance magic.◼

Proof. Suppose that $G = {C_{3}}^{t} \times C_{4}$ is a distance magic graph under distance magic labeling f and that magic constant is γ. We have

$\begin{aligned} γ = w (r^{0}) = \sum_{k = 1}^{t} (f (p_{k}^{1}) + f (q_{k}^{1}) + f (p_{k}^{3}) + f (q_{k}^{3})) \\ = w (r^{1}) = \sum_{k = 1}^{t} (f (p_{k}^{0}) + f (q_{k}^{0}) + f (p_{k}^{2}) + f (q_{k}^{2})) \end{aligned}$	(16.5)

and

$\begin{aligned} w (p_{k}^{0}) = f (q_{k}^{1}) + f (q_{k}^{3}) + f (r^{1}) + f (r^{3}), \\ w (q_{k}^{0}) = f (p_{k}^{1}) + f (p_{k}^{3}) + f (r^{1}) + f (r^{3}), \\ w (p_{k}^{1}) = f (q_{k}^{0}) + f (q_{k}^{2}) + f (r^{0}) + f (r^{2}), \\ w (q_{k}^{1}) = f (p_{k}^{0}) + f (p_{k}^{2}) + f (r^{0}) + f (r^{2}) \end{aligned}$	(16.6)

which implies that

$\begin{aligned} w (r^{0}) = \sum_{k = 1}^{t} (w (p_{k}^{0}) + w (q_{k}^{0})) - 2 t (f (r^{1}) + f (r^{3})) \\ = w (r^{1}) = \sum_{k = 1}^{t} (w (p_{k}^{1}) + w (q_{k}^{1})) - 2 t (f (r^{0}) + f (r^{2})) \end{aligned}$	(16.7)

so that,

$\begin{aligned} 2 t γ - 2 t (f (r^{1}) + f (r^{3})) = 2 t γ - 2 t (f (r^{0}) + f (r^{2})) \end{aligned}$	(16.8)

Thus,

$f (r^{0}) + f (r^{2}) = f (r^{1}) + f (r^{3}) = δ (say)$	(16.9)

Now, for all k = 1, 2, …, t and j ≡ 0(mod4)

$\begin{aligned} w (p_{k}^{j}) = f (q_{k}^{j - 1}) + f (q_{k}^{j + 1}) + f (r^{j - 1}) + f (r^{j + 1}), \\ w (q_{k}^{j}) = f (p_{k}^{j - 1}) + f (p_{k}^{j + 1}) + f (r^{j - 1}) + f (r^{j + 1}) \end{aligned}$	(16.10)

But $w (p_{k}^{j}) = w (q_{k}^{j})$ . So,

$\begin{aligned} f (p_{k}^{j - 1}) + f (p_{k}^{j + 1}) = f (q_{k}^{j - 1}) + f (q_{k}^{j + 1}) = μ (say), \forall k, j \end{aligned}$	(16.11)

By Equations (16.5) and (16.11)

γ = 2 t μ

and by Equations, (16.9), (16.10) and (16.11)

γ = δ + μ

Now, by the above two equations, we get

$μ = \frac{δ}{2 t - 1}$	(16.12)

Let us find the sum of labels of all vertices except r^j vertices.

$\sum_{\begin{matrix} k = 1 \\ j = 0, 1, 2, 3 \end{matrix}}^{t} (f (p_{k}^{j}) + f (q_{k}^{j})) = \frac{(8 t + 4) (8 t + 5)}{2} - (f (r^{0}) + f (r^{2}) + f (r^{1}) + f (r^{3})),$	(16.13)

since, |V(G)| = 8t + 4.

By (16.9) and (16.11), we get

$4 t μ = \frac{(8 t + 4) (8 t + 5)}{2} - 2 δ$	(16.14)

Thus, by Equations (16.12)

$δ = \frac{32 t^{3} + 20 t^{2} - 8 t - 5}{4 t - 1}$	(16.15)

i.e.,

$f (r^{0}) + f (r^{2}) = f (r^{1}) + f (r^{3}) = \frac{32 t^{3} + 20 t^{2} - 8 t - 5}{4 t - 1}$	(16.16)

Now, f(r⁰), f(r²) ∈ {1, 2, …, 8t + 4}. If we take f(r⁰) = 8t + 4 and f(r²) = 8t + 3, then f(r⁰) + f(r²) = δ = 16t + 7, which is less than $\frac{32 t^{3} + 20 t^{2} - 8 t - 5}{4 t - 1}$ . So, equality in (16.16) cannot possible.

Hence, ${C_{3}}^{t} \times C_{4}$ is not a distance magic graph.□

Here, the graph ${C_{3}}^{t} \times C_{4}$ is not a distance magic graph as well as by Lemma 16.3 it is not distance antimagic because neighborhoods of vertex $p_{k}^{0}$ and $p_{k}^{2}$ , for k = 1, 2, …, t are always the same.

16.4Strong Product of $C_{3}^{t}$ and C₄

Theorem 16.4

The graph $C_{3}^{t} ⊠ C_{4}$ is distance antimagic.◼

Proof. We define a vertex labeling f:V(G) → {1, 2, …, |V(G)|} as follows:

For 1 ≤ k ≤ t and j ≡ 0(mod4)

\begin{aligned} f (p_{k}^{j}) = 2 j t + 2 t - k + 1; \\ f (q_{k}^{j}) = 2 j t + k; \\ f (r^{j}) = 8 t - j + 4 \end{aligned}

Under the above labeling, weights for each vertex are as follows:

For 1 ≤ k ≤ t, j ≡ 0(mod4),

\begin{aligned} w (p_{k}^{j}) = 28 t + k + 14 + 2 j t + 4 (j + 1) t + 4 (j - 1) t - j - (j + 1) - (j - 1); \\ w (q_{k}^{j}) = 30 t - k + 15 + 2 j t + 4 (j + 1) t + 4 (j - 1) t - j - (j + 1) - (j - 1); \\ w (r^{j}) = 6 t^{2} + 19 t + 8 + 4 j t^{2} + 4 (j + 1) t^{2} + 4 (j - 1) t^{2} - (j + 1) - (j - 1) \end{aligned}

Here, we can see that, each vertex has distinct weights.

Therefore, the graph $C_{3}^{t} ⊠ C_{4}$ is a distance antimagic graph.□

Illustration 16.4.1. The graph $C_{3}^{2} ⊠ C_{4}$ with distance antimagic labeling is given in Figure 16.2.

Figure 16.2: The distance antimagic labeling of $C_{3}^{2} ⊠ C_{4}$

Here, the graph $C_{3}^{t} ⊠ C_{4}$ is distance antimagic but it is not distance magic. Since for this graph, $| N (p_{1}^{0}) \cap N (q_{1}^{0}) | = d (p_{1}^{0}) - 1 = d (q_{1}^{0}) - 1$ , so by Lemma 16.2 it is not a distance magic graph.

16.5Corona Product of C₄ and $C_{3}^{t}$

Theorem 16.5

The graph $C_{4} ⊙ C_{3}^{t}$ is distance antimagic.◼

Proof. Let $G = C_{4} ⊙ {C_{3}}^{t}$ and vertex set $V (G) = {p_{k}^{j}, q_{k}^{j}, r^{j}, c_{j} | 1 \leq k \leq t, 0 \leq j \leq 3}$ where $p_{k}^{j}, q_{k}^{j}, r^{j} (1 \leq k \leq t)$ are the vertices of the (j + 1)^th copy of ${C_{3}}^{t}$ which are adjacent to vertex c_j of C₄ for j = 0, 1, 2, 3.

We define a vertex labeling f:V(G) → {1, 2, …, |V(G)|} as follows:

For, 1 ≤ k ≤ t and j ≡ 0(mod4),

\begin{aligned} f (p_{k}^{j}) & = j + 8 k - 3; \\ f (q_{k}^{j}) & = j + 8 k + 1; \\ f (r^{j}) & = 8 t - j + 8; \\ f (c_{j}) & = 4 - j \end{aligned}

Under the above labeling, weights for each vertex are as follows:

For 1 ≤ k ≤ t and j ≡ 0(mod4),

\begin{aligned} w (p_{k}^{j}) = 8 t + 8 k - j + 13; \\ w (q_{k}^{j}) = 8 t + 8 k - j + 9; \\ w (r^{j}) = 8 t^{2} + 6 t + 2 t j - j + 4; \\ w (c_{j}) = 8 t^{2} + 14 t + 2 t j - (j + 1) - j - (j - 1) + 16 \end{aligned}

One can easily verify that, all weights are distinct.

Hence, the graph $C_{4} ⊙ C_{3}^{t}$ is a distance antimagic graph.□

Illustration 16.5.1. The distance antimagic labeling for $C_{4} ⊙ C_{3}^{2}$ is given in Figure 16.3.

Figure 16.3: The distance antimagic labeling of $C_{4} ⊙ C_{3}^{2}$

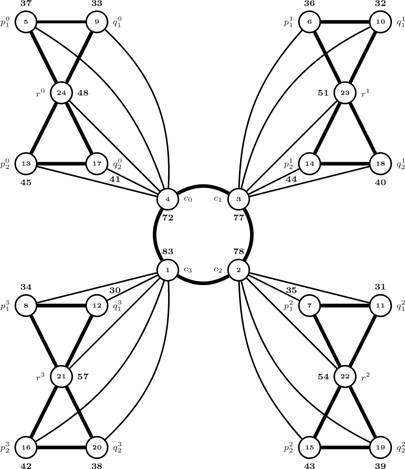
The corona product of C₄ and $C_{3}^{t}$ is a distance antimagic graph but it is not a distance magic graph by Lemma 16.2, since $| N (p_{1}^{0}) \cap N (q_{1}^{0}) | = d (p_{1}^{0}) - 1 = d (q_{1}^{0}) - 1$ .

16.6Concluding Remark

Here, we have investigated the existence of distance magic labeling and distance antimagic labeling of certain products of the friendship graph and cycle C₄. To explore some new distance magic and distance antimagic graphs is an open problem.

References

1.B. Acharya, S. Rao, T. Singh and V. Parameswaran. Neighbourhood magic graphs. National Conference on Graph Theory, Combinatorics and Algorithm, 2004.

2.M. Anholcer and S. Cichacz. Note on distance magic products G ∘ C₄. Graphs and Combinatorics, 31, 1117-1124, 2015.

3.D. M. Burton. Elementary Number Theory. Tata McGraw-Hill, 2007.

4.J. A. Gallian. A dynamic survey of graph labeling. The Electronics Journal of Combinatorics, # DS6, 2018.

5.J. Gross and J. Yellen. Graph Theory and its Applications. CRC Press, 2005.

6.R. Hammack, W. Imrich and S. Klavžar. Handbook of Product Graphs, CRC Press, Boca Raton, FL. 2011.

7.M. Miller, C. Rodger and R. Simanjuntak. Distance magic labeling of graphs. Australas. J. Combin., 28, 305-315, 2003.

8.R. Simanjuntak and K. Wijaya. On distance antimagic graphs. arXiv:1312.7405v1[math.CO], 2013.

9.K. Sugeng, D. Fronček, M. Miller, J. Ryan and J. Walker. On distance magic labeling of graphs. Journal of Combinatorial Mathematics and Combinatorial Computing, 71, 39-48, 2009.

10.V. Vilfred. Σ-labelled Graphs and Circulant Graphs. Ph.D. Thesis, University of Kerala, Trivandrum, India 1994.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 16: Distance Magic and Distance Antimagic Labeling of Some Product Graphs

Create new playlist

Sign In

Sign Up

Table of Contents for
Chapter 16: Distance Magic and Distance Antimagic Labeling of Some Product Graphs