CHAPTER 4
CHAPTER 4
Accounting for Body Dynamics: The Jogger's Problem
Let me first explain to you how the motions of different kinds of matter depend on a property called inertia.
— Sir William Thomson (Lord Kelvin), The Tides
4.1 PROBLEM STATEMENT
As discussed before, motion planning algorithms usually adhere to one of the two paradigms that differ primarily by their assumptions about input information: motion planning with complete information (Piano Mover's problem) and motion planning with incomplete information (sensor-based motion planning, SIM paradigm, see Chapter 1). Strategies that come out of the two paradigms can be also classified into two groups: kinematic approaches, which consider only kinematic and geometric issues, and dynamic approaches, which take into account the system dynamics. This classification is independent from the classification into the two paradigms. In Chapter 3 we studied kinematic sensor-based motion planning algorithms. In this chapter we will study dynamic sensor-based motion planning algorithms.
What is so dynamic about dynamic approaches? In strategies that we considered in Chapter 3, it was implicitly assumed that whatever direction of motion is good for the robot's next step from the standpoint of its goal, the robot will be able to accomplish it. If this is true, in the terminology of control theory such a system is called a holonomic system [78]. In a holonomic system the number of control variables available is no less that the problem dimensionality. The system will also work as intended in situations where the above condition is not satisfied, but for some reason the robot dynamics can be ignored. For example, a very slowly moving robot can turn on a dime and hence can execute any sharp turn if prescribed by its motion planning software.
Most of existing approaches to motion planning (including those within the Piano Mover's model) assume, first, that the system is holonomic and, second, that it will behave as a holonomic system. Consequently, they deal solely with the system kinematics and ignore its dynamic properties. One reason for this state of affairs is that the methods of motion planning tend to rely on tools from geometry and topology, which are not easily connected to the tools common to control theory. Although system dynamics and sensor-based motion control are clearly tightly coupled in many, if not most, real-world systems, little attention has been paid to this connection in the literature.
The robot is a body; it has a mass and dimensions. Once it starts moving, it acquires velocity and acceleration. Its dynamics may now prevent it from making sharp, and sometimes even relatively shallow, turns prescribed by the planning algorithm. A sharp turn reasonable from the standpoint of reaching the target position may not be physically realizable because of the robot's inertia. In control theory terminology, this is a nonholonomic system [78]. A classical example of a nonholonomic control problem is the car parallel parking task: Because the driver does not have enough control means to execute the parking in one simple translational motion, he has to wiggle the car back and force to bring it to the desired position.
Given the insufficient information about the surroundings, which is central to the sensor-based motion planning paradigm, the lack of control means to execute any desired motion translates into a safety issue: One needs a guarantee of a stopping path at any time, in case a sudden obstacle makes it impossible to continue on the intended path.
Theoretically, there is a simple way out: We can make the robot stop every time it intends to turn, let it turn, and resume the motion as needed. Not many applications will like such a stop-and-go motion pattern. For a realistic control we want the robot to make turns on the move, and not stop unless “absolutely necessary,” whatever this means. That is, in addition to the usual problem of “where to go” and how to guarantee the algorithm convergence in view of incomplete information, the robot's mass and velocity bring about another component of motion planning, body dynamics. Furthermore, we will see that it will be important to incorporate the constraints of robot dynamics into the very motion planning algorithm, together with the constraints dictated by collision avoidance and algorithm convergence requirements.
We call the problem thus formulated the Jogger's Problem, because it is not unlike the task a human jogger faces in an urban setting when going for a morning run. Taking a run involves continuous on-line control and decision-making. Many decisions will be made during the run; in fact, many decisions are made within each second of the run. The decision-making apparatus requires a smooth collaboration of a few mechanisms. First, a global planning mechanism will work on ensuring arrival at the target location in spite of all deviations and detours that the environment may require. Unless a “grand plan” is followed, arrival at the target location—what we like to call convergence—may not be guaranteed.
Second, since an instantaneous stop is impossible due to the jogger's inertia, in order to maintain a reasonable speed the jogger needs at any moment an “insurance” option of a safe stopping path. This mechanism will relate the jogger's mass and speed to the visible field of view. It is better to slow down at the corner—who knows what is behind the corner?
Third, when the jogger starts turning the street corner and suddenly sees a pile of sand right on the path that he contemplated (it was not there last time), some quick local planning must occur to take care of collision avoidance. The jogger's speed may temporarily decrease and the path will smoothly divert from the object. The jogger will likely want to locally optimize this path segment, in order to come back to his preplanned path quicker or along a shorter path. Other options not being feasible, the jogger may choose to “brake” to a halt and start a detour path.
As we see, the jogger's speed, mass, and quality of vision, as well as the speed of reaction to sudden changes—which represents the quality of his control system—are all tied together in a certain relationship, affecting the real-time decision-making process. The process will go on nonstop, all the time; the jogger cannot afford to take his eyes off the route for more than a fraction of a second. Sensing, local planning, global planning, and actual movement are in this process taking place simultaneously and continuously. Locally, unless the right relationship is maintained between the velocity when noticing an object, the distance to it, and the jogger's mass, collision may occur. A bigger mass may dictate better (farther) sensing to maintain the same velocity. Myopic vision may require reducing the speed.
Another interesting detail is that in the motion planning strategies considered in Chapter 3, each step of the path could be decided independently from other steps. The control scheme that takes into account robot dynamics cannot afford such luxury anymore. Often a decision will likely affect more than calculation of the current step. Consider this: Instead of turning on the dime as in our prior algorithms, the robot will be likely moving along relatively smooth curves. How do we know that the smooth path curve dictated by robot dynamics at the current step will not be in conflict with collision considerations at the next step? Perhaps at the current step we need to think of the next step as well. Or perhaps we need to think of more than one step ahead. Worse yet, what if a part of that path curve cannot be checked because it is bending around the corner of a nearby obstacle and hence is invisible?
These questions suggest that in a planning/control system with included dynamics a path step cannot be planned separately from at least a few steps that will follow it. The robot must make sure that the step it now contemplates will not result in some future steps where the collision is inevitable. How many steps look-ahead is enough? This is one thing that we need to figure out.
Below we will study the said effects, with the same objective as before—to design provably correct sensor-based motion planning algorithms. As before, the presence of uncertainty implies that no global optimality of the path is feasible. Notice, however, that given the need to plan for a few steps ahead, we can attempt local optimization. While improving the overall path, sometimes dramatically, in general a path segment that is optimal within the robot's field of vision says nothing about the path global optimality.
By the way, which optimization criterion is to be used? We will consider two criteria. The salient feature of one criterion is that, while maintaining the maximum velocity allowed by its dynamics, the robot will attempt to maximize its instantaneous turning angle toward the required direction of motion. This will allow it to finish every turning maneuver in minimum time. In a path with many turns, this should save a good deal of time. In the second strategy (which also assumes the maximum velocity compatible with collision avoidance), the robot will attempt a time-optimal arrival at its (constantly shifting) intermediate target. Intermediate targets will typically be on the boundary of the robot's field of vision.
Similar to the model used in Chapter 3, our mobile robot operates in two-dimensional physical space filled with a locally finite number of unknown stationary obstacles of arbitrary shapes. Planning is done in small steps (say, 30 or 50 times per second, which is typical for real-world robotics), resulting in continuous motion. The robot is equipped with sensors, such as vision or range finders, which allow it to detect and measure distances to surrounding objects within its sensing range. Robot vision works within some limited or unlimited radius of vision, which allows some steps look-ahead (say, 20 or 30 or more). Unless obstacles occlude one another, the robot will see them and use this information to plan appropriate actions. Occlusions effectively limit a robot's input information and call for more careful planning.
Control of body dynamics fits very well into the feedback nature of the SIM (Sensing-Intelligence-Motion) paradigm. To be sure, such control can in principle be incorporated in the Piano Mover's paradigm as well. One way to do this is, for example, to divide the motion planning process into two stages: First, a path is produced that satisfies the geometric constraints, and then this path is modified to fit the dynamic constraints [79], possibly in a time-optimal fashion [80–82].
Among the first attempts to explicitly incorporate body dynamics into robot motion planning were those by O'Dunlaing [83] for the one-dimensional case and by Canny et al. [84] in their kinodynamic planning approach for the two-dimensional case. In the latter work the proposed algorithm was shown to run in exponential time and to require space that is polynomial in the input. While the approach operates in the context of the Piano Mover's paradigm, it is somewhat akin to the approach considered in this chapter, in that the control strategy adheres to the L∞-norm; that is, the velocity and acceleration components are assumed bounded with respect to a fixed (absolute) reference system. This allows one to decouple the equations of robot motion and treat the two-dimensional problem as two one-dimensional problems.1
Within the Piano Mover's paradigm, a number of kinematic holonomic strategies make use of the artificial potential field. They usually require complete information and analytical presentation of obstacles; the robot's motion is affected by (a) the “repulsive forces” created by a potential field associated with obstacles and (b) “attractive forces” associated with the goal position [85]. A typical convergence issue here is how to avoid possible local minima in the potential field. Modifications that attempt to solve this problem include the use of repulsive fields with elliptic isocontours [86], introduction of special global fields [87], and generation of a numerical field [88]. The vortex field method [89] allows one to avoid undesirable attraction points, while using only local information; the repulsive actions are replaced by the velocity flows tangent to the isocontours, so that the robot is forced to move around obstacles. An approach called active reflex control [90] attempts to combine the potential field method with handling the robot dynamics; the emphasis is on local collision avoidance and on filtering out infeasible control commands generated by the motion planner.
Among the approaches that deal with incomplete information, a good number of holonomic techniques originate in maze-search strategies (see the previous chapters). When applicable, they are usually fast, can be used in real time, and guarantee convergence; obstacles in the scene may be of arbitrary shape.
There is also a group of nonholonomic motion planning approaches that ignore the system dynamics. These also require analytical representation of obstacles and assume complete [91–93] or partial input information [94]. The schemes are essentially open-loop, do not guarantee convergence, and attempt to solve the planning problem by taking into account the effect of nonholonomic constraints on obstacle avoidance. In Refs. 91 and 92 a two-stage scheme is considered: First, a holonomic planner generates a complete collision-free path, and then this path is modified to account for nonholonomic constraints. In Ref. 93 the problem is reduced to searching a graph representing the discretized configuration space. In Ref. 94, planning is done incrementally, with partial information: First, a desirable path is defined and then a control is found that minimizes the error in a least-squares sense.
To design a provably correct dynamic algorithm for sensor-based motion planning, we need a single control mechanism: Separating it into stages is likely to destroy convergence. Convergence has two faces: Globally, we have to guarantee finding a path to the target if one exists. Locally, we need an assurance of collision avoidance in view of the robot inertia. The former can be borrowed from kinematic algorithms; the latter requires an explicit consideration of dynamics.
Notice an interesting detail: In spite of sufficient knowledge about the piece of the scene that is currently within the robot's sensing range, even in this area it would make little sense at a given step to address the planning task as one with complete information, as well as to try to compute the whole subpath within the sensing range. Why not? Computing this subpath would require solving a rather difficult optimal motion control problem—a computationally expensive task. On the other hand, this would be largely computational waste, because only the first step of this subpath would be executed: As new sensing data appears at the next step, in general a path adjustment would be required. We will therefore attempt to plan only as many steps that immediately follow the current one as is needed to guarantee nonstop collision-free motion.
The general approach will be as follows: At its current position Ci, the robot will identify a visible intermediate target point, Ti, that is guaranteed to lie on a convergent path and is far enough from the robot—normally at the boundary of the sensing range. If the direction toward Ti differs from the current velocity vector Vi, moving toward Ti may require a turn, which may or may not be possible due to system dynamics.
In the first strategy that we will consider, if the angle between Vi and the direction toward Ti is larger than the maximum turn the robot can make in one step, the robot will attempt a fast smooth maneuver by turning at the maximum rate until the directions align; hence the name Maximum Turn Strategy. Once a step is executed, new sensing data appear, a new point Ti+1 is sought, and the process repeats. That is, the actual path and the path that contains points Ti will likely be different paths: With the new sensory data at the next step, the robot may or may not be passing through point Ti.
In the second strategy, at each step, a canonical solution is found which, if no obstacles are present, would bring the robot from its current position Ci to the intermediate target Ti with zero velocity and in minimum time. Hence the name Minimum Time Strategy. (The minimum time refers of course to the current local piece of scene.) If the canonical path crosses an obstacle and is thus not feasible, a near-canonical solution path is found which is collision-free and satisfies the control constraints. We will see that in this latter case only a small number of options needs be considered, at least one of which is guaranteed to be collision-free.
The fact that no information is available beyond the sensing range dictates caution. To guarantee safety, the whole stopping path must not only lie inside the sensing range, it must also lie in its visible part. No parts of the stopping path can be occluded by obstacles. Moreover, since the intermediate target Ti is chosen as the farthest point based on the information currently available, the robot needs a guarantee of stopping at Ti, even if it does not intend to do so. Otherwise, what if an obstacle lurks right beyond the vision range? That is, each step is to be planned as the first step of a trajectory which, given the current position, velocity, and control constraints, would bring the robot to a halt at T. Within one step, the time to acquire sensory data and to calculate necessary controls must fit into the step cycle.
4.2 MAXIMUM TURN STRATEGY
4.2.1 The Model
The robot is a point mass, of mass m. It operates in the plane; the scene may include a locally finite number of static obstacles. Each obstacle is bounded by a simple closed curve of arbitrary shape and of finite length, such that a straight line will cross it in only a finite number of points. Obstacles do not touch each other; if they do, they are considered one obstacle. The total number of obstacles in the scene need not be finite.
The robot's sensors provide it with information about its surroundings within the sensing range (radius of vision), a disc of radius rυ centered at its current location Ci. The sensor can assess the distance to the nearest obstacle in any direction within the sensing range. The robot input information at moment ti includes its current velocity vector Vi, coordinates of point Ci and of the target point T, and possibly few other points of interest that will be discussed later.
The task is to move, collision-free, from point S (start) to point T (target) (see Figure 4.1). The robot's control means include two components (p, q) of the acceleration vector ![]() , where m is the robot mass and f is the force applied. Though the units of (p, q) are those of acceleration, by normalizing to m = 1 we can refer to p and q as control forces, each within its fixed range |p| ≤ pmax, |q| ≤ qmax. Force p controls forward (or backward when braking) motion; its positive direction coincides with the velocity vector V. Force q is perpendicular to p, forming a right pair of vectors, and is equivalent to the steering control (rotation of vector V) (Figure 4.2). Constraints on p and q imply a constraint on the path curvature. The point mass assumption implies that the robot's rotation with respect to its “center of mass” has no effect on the system dynamics. There are no external forces acting on the robot except p and q. There is no friction; for example, values p = q = 0 and V ≠ 0 will result in a straight-line constant velocity motion.2
, where m is the robot mass and f is the force applied. Though the units of (p, q) are those of acceleration, by normalizing to m = 1 we can refer to p and q as control forces, each within its fixed range |p| ≤ pmax, |q| ≤ qmax. Force p controls forward (or backward when braking) motion; its positive direction coincides with the velocity vector V. Force q is perpendicular to p, forming a right pair of vectors, and is equivalent to the steering control (rotation of vector V) (Figure 4.2). Constraints on p and q imply a constraint on the path curvature. The point mass assumption implies that the robot's rotation with respect to its “center of mass” has no effect on the system dynamics. There are no external forces acting on the robot except p and q. There is no friction; for example, values p = q = 0 and V ≠ 0 will result in a straight-line constant velocity motion.2
Robot motion is controlled in steps i, i = 0, 1, 2,…. Each step takes time δt = ti+1 − ti = const. The step's length depends on the robot's velocity within the step. Steps i and i + 1 start at times ti and ti+1, respectively; C0 = S. While moving toward location Ci+1, the robot computes necessary controls for step i + 1 using the current sensory data, and it executes them at Ci+1. The finite time necessary within one step for acquiring sensory data, calculating the controls, and executing the step must fit into the step cycle (more details on this can be found in Ref. 96). We define two coordinate systems (follow Figure 4.2):
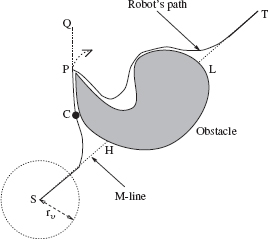
Figure 4.1 An example of a conflict between the performance of a kinematic algorithm (e.g., VisBug-21, the solid line path) and the effects of dynamics (the dotted piece of trajectory at P).
Figure 4.2 The path coordinate frame (t, n) is used in the analysis of dynamic effects of robot motion. The world frame (x, y), with its origin at the start point S, is used in the obstacle detection and path planning analysis.
- The world coordinate frame, (x, y), fixed at point S.
- The path coordinate frame, (t, n), which describes the motion of point mass at any moment τ ∈ [ti, ti+1) within step i. The frame's origin is attached to the robot; axis t is aligned with the current velocity vector V; axis n is normal to t; that is, when V = 0, the frame is undefined. One may note that together with axis b = t × n, the triple (t, n, b) forms the known Frenet trihedron, with the plane of t and n being the osculating plane [97].
4.2.2 Sketching the Approach
Some terms and definitions here are the same as in Chapter 3; material in Section 3.1 can be used for more rigorous definitions. Define M-line (Main line) as the straight-line segment (S, T) (Figure 4.1). The M-line is the robot's desired path. When, while moving along the M-line, the robot senses an obstacle crossing the M-line, the crossing point on the obstacle boundary is called a hit point, H. The corresponding M-line point “on the other side” of the obstacle is a leave point, L.
The planning procedure is to be executed at each step of the robot's path. Any provable maze-searching algorithm can be used for the kinematic part of the algorithm that we are about to build, as long as it allows distant sensing. For specificity only, we use here the VisBug algorithm (see Section 3.6; either VisBug-21 or VisBug-22 will do). VisBug algorithms alternate between these two operations (see Figure 4.1):
- Walk from point S toward point T along the M-line until, at some point C, you detect an obstacle crossing the M-line, say at point H.
- Using sensing data, define the farthest visible intermediate target Ti on the obstacle boundary and on a convergent path; make a step toward Ti; iterate Step 2 until you detect the M-line; go to Step 1.
To this process we add a control procedure for handling dynamics. It is clear already that from time to time dynamics will prevent the robot from carefully following an obstacle boundary. For example, in Figure 4.1, while trying to pass the obstacle from the left, under a VisBug procedure the robot would make a sharp turn at point P. Such motion is not possible in a system with dynamics.
At times the current intermediate target Ti may go out of the robot's sight, because of the robot inertia or because of occluding obstacles. In such cases the robot will be designating temporary intermediate targets and use them until it can spot the point Ti again. The final algorithm will also include mechanisms for checking the target reachability and for local path optimization.
Safety Considerations. Dynamics affects safety. Given the uncertainty beyond the distance rυ from the robot (or even closer to it in case of occluding obstacles), a guaranteed stopping path is the only way to ensure collision-free motion. Unless this last resort path is available, new obstacles may appear in the sensing range at the next step, and collision may be imminent. A stopping path implies a safe direction of motion and a safe velocity value. We choose the stopping path as a straight-line segment along the step's velocity vector. A candidate for the next step is “approved” by the algorithm only if its execution would guarantee a stopping path. In this sense our planning procedure is based on a one-step analysis.3
As one will see, the procedure for a detour around a suddenly appearing obstacle operates in a similar fashion. We emphasize that the stopping path does not mean stopping. While moving along, at every step the robot just makes sure that if a stop is suddenly necessary, there is always a guarantee for it.
Allowing for a straight-line stopping path with the stop at the sensing range boundary implies the following relationship between the velocity V, mass m, and controls u = (p, q):
where d is the distance from the current position C to the stop point. So, for example, an increase in the radius of vision rυ would allow the robot to raise the maximum velocity, by the virtue of providing more information farther along the path. Some control ramifications of this relationship will be analyzed in Section 4.2.3.
Convergence. Because of the effect of dynamics, the convergence mechanism borrowed from a kinematic algorithm—here VisBug—needs some modification. VisBug assumes that the intermediate target point is either on the obstacle boundary or on the M-line and is visible. However, the robot's inertia may cause it to move so that the intermediate target Ti will become invisible, either because it goes outside the sensing range rυ (as after point P, Figure 4.1) or due to occluding obstacles (as in Figure 4.6). The danger of this is that the robot may lose from its sight point Ti—and the path convergence with it. One possible solution is to keep the velocity low enough to avoid such overshoots—a high price in efficiency to pay. The solution we choose is to keep the velocity high and, if the intermediate target Ti does go out of sight, modify the motion locally until Ti is found again (Section 4.2.6).
4.2.3 Velocity Constraints. Minimum Time Braking
By substituting pmax for p and rυ for d into (4.1), one obtains the maximum velocity, Vmax. Since the maximum distance for which sensing information is available is rυ, the sensing range boundary, an emergency stop should be planned for that distance. We will show that moving with the maximum speed—certainly a desired feature—actually guarantees a minimum-time arrival at the sensing range boundary. The suggested braking procedure, developed fully in Section 4.2.4, makes use of an optimization scheme that is sketched briefly in Section 4.2.4.
Velocity Constraints. It is easy to see (follow an example in Figure 4.3) that in order to guarantee a safe stopping path, under discrete control the maximum velocity must be less than Vmax. This velocity, called permitted maximum velocity, Vp max, can be found from the following condition: If V = Vp max at point C2 (and thus also at C1), we can guarantee the stop at the sensing range boundary (point B1, Figure 4.3). Recall that velocity V is generated at C1 by the control force p. Let |C1C2| = δx; then
![]()
Since we require VB1 = 0, then t = Vp max/pmax. For the segment |C2B1| = rυ − δx, we have
![]()
From these equations, the expression for the maximum permitted velocity Vp max can be obtained:
![]()
As expected, Vpmax < Vmax and converges to Vmax with δt → 0.
Figure 4.3 With the sensing radius equal to rυ, obstacle O1 is not visible from point C1. Because of the discrete control, velocity V1 commanded at C1 will be constant during the step interval (C1, C2). Then, if V1 = Vmax at C1, then also V2 = Vmax, and the robot will not be able to stop at B1, causing collision with obstacle O1. The permitted velocity thus must be Vp max < Vmax.
4.2.4 Optimal Straight-Line Motion
We now sketch the optimization scheme that will later be used in the development of the braking procedure. Consider a dynamic system, a moving body whose behavior is described by a second-order differential equation ![]() , where || p(t) || ≤ pmax and p(t) is a scalar control function. Assume that the system moves along a straight line. By introducing state variables x and V, the system equations can be rewritten as
, where || p(t) || ≤ pmax and p(t) is a scalar control function. Assume that the system moves along a straight line. By introducing state variables x and V, the system equations can be rewritten as ![]() and
and ![]() . It is convenient to analyze the system behavior in the phase space (V, x).
. It is convenient to analyze the system behavior in the phase space (V, x).
The goal of control is to move the system from its initial position (x(t0), V(t0)) to its final position (x(tf), V(tf)). For convenience, choose x(tf) = 0. We are interested in an optimal control strategy that would execute the motion in minimum time tf, arriving at x(tf) with zero velocity, V(tf) = 0. This optimal solution can be obtained in closed form; it depends upon the above/below relation of the initial position with respect to two parabolas that define the switch curves in the phase plane (V, x):
This simple result in optimal control (see, e.g., Ref. 98) is summarized in the control law that follows, and it is used in the next section in the development of the braking procedure for emergency stopping. The procedure will guarantee robot safety while allowing it to cruise with the maximum velocity (see Figure 4.4):
Figure 4.4 Depending on whether the initial position (V0, x0) in the phase space (V, x) is above or below the switch curves, there are two cases to consider. The optimal solution corresponds to moving first from point (V0, x0) to the switching point (Vs, xs) and then along the switch line to the origin.
Control Law: If in the phase space the initial position (V0, x0) is above the switch curve (4.2), first move along the parabola defined by control ![]() toward curve (4.2), and then with control
toward curve (4.2), and then with control ![]() move along the curve to the origin. If point (V0, x0) is below the switch curve, move first with control
move along the curve to the origin. If point (V0, x0) is below the switch curve, move first with control ![]() toward the switch curve (4.3), and then move with control
toward the switch curve (4.3), and then move with control ![]() along the curve to the origin.
along the curve to the origin.
The Braking Procedure. We now turn to the calculation of time it will take the robot to stop when it moves along the stopping path. It follows from the argument above that if at the moment when the robot decides to stop its velocity is V = Vpmax, then it will need to apply maximum braking all the way until the stop. This will define uniquely the time to stop. But, if V < Vp max, then there are a variety of braking strategies and hence of different times to stop.
Consider again the example in Figure 4.3; assume that at point C2, V2 < Vp max. What is the optimal braking strategy, the one that guarantees safety while bringing the robot in minimum time to a stop at the sensing range boundary? While this strategy is not necessarily the one we would want to implement, it is of interest because it defines the limit velocity profile the robot can maintain for safe braking. The answer is given by the solution of an optimization problem for a single-degree-of-freedom system. It follows from the Control Law above that the optimal solution corresponds to at most two curves, I and II, in the phase space (V, x) (Figure 4.5a) and to at most one control switch, from ![]() on line I to
on line I to ![]() on line II, given by (4.2) and (4.3). For example, if braking starts with the initial values x = −rυ and 0 ≤ V0 < Vmax, the system will first move, with control
on line II, given by (4.2) and (4.3). For example, if braking starts with the initial values x = −rυ and 0 ≤ V0 < Vmax, the system will first move, with control ![]() , along parabola I to parabola II (Figure 4.5a),
, along parabola I to parabola II (Figure 4.5a),
Figure 4.5 (a) Optimal braking strategy requires at most one switch of control. (b) The corresponding time-velocity relation.
![]()
and then, with control ![]() , toward the origin, along parabola II,
, toward the origin, along parabola II,
![]()
The optimal time tb of braking is a function of the initial velocity V0, radius of vision rυ, and the control limit pmax,
Function tb(V0) has a minimum at ![]() which is exactly the upper bound on the velocity given by (4.1); it is decreasing on the interval V0 ∈ [0, Vmax] and increasing when V0 > Vmax (see Figure 4.5b). For the interval V0 ∈ [0, Vmax], which is of interest to us, the above analysis leads to a somewhat counterintuitive conclusion:
which is exactly the upper bound on the velocity given by (4.1); it is decreasing on the interval V0 ∈ [0, Vmax] and increasing when V0 > Vmax (see Figure 4.5b). For the interval V0 ∈ [0, Vmax], which is of interest to us, the above analysis leads to a somewhat counterintuitive conclusion:
Proposition 1. For the initial velocity V0 in the range V0 ∈ [0, Vmax], the time necessary for stopping at the boundary of the sensing range is a monotonically decreasing function of V0, with its minimum at V0 = Vmax.
Notice that this result (see also Figure 4.5) leaves a comfortable margin of safety: Even if at the moment when the robot sees an obstacle on its way it moves with the maximum velocity, it can still stop safely before it reaches the obstacle. If the robot's velocity is below the maximum, it has more control options for braking, including even one of speeding up before actual braking. Assume, for example, that we want the robot to stop in minimum time at the sensing range boundary (the origin in Figure 4.5a); consider two initial positions: ![]() and
and ![]() . Then, according to Proposition 1, in case (i) this time is bigger than in case (ii). Note that because of the discrete control it is the permitted maximum velocity, Vp max, that is to be substituted into (4.4) to obtain the minimum time. (More details on the braking procedure can be found in Ref. 99).
. Then, according to Proposition 1, in case (i) this time is bigger than in case (ii). Note that because of the discrete control it is the permitted maximum velocity, Vp max, that is to be substituted into (4.4) to obtain the minimum time. (More details on the braking procedure can be found in Ref. 99).
4.2.5 Dynamics and Collision Avoidance
The analysis in this section consists of two parts. First we incorporate the control constraints into the model of our mobile robot and develop a transformation from the moving path coordinate frame to the world frame (see Section 4.2.1). Then the Maximum Turn Strategy is produced, an incremental decision-making mechanism that determines forces p and q at each step.
Transformation from Path Frame to World Frame. The remainder of this section refers to the time interval [ti, ti+1), and so index i can be dropped. Let ![]() be the robot's position in the world frame, and let θ be the (slope) angle between the velocity vector
be the robot's position in the world frame, and let θ be the (slope) angle between the velocity vector ![]() and x axis of the world frame (see Figure 4.2). The planning process involves computation of controls u = (p, q), which for every step defines the velocity vector and eventually the path, x = (x, y), as a function of time. The normalized equations of motion are
and x axis of the world frame (see Figure 4.2). The planning process involves computation of controls u = (p, q), which for every step defines the velocity vector and eventually the path, x = (x, y), as a function of time. The normalized equations of motion are
![]()
The angle θ between vector V and x axis of the world frame is found as

To find the transformation from path frame to the world frame (x, y), present the velocity in the path frame as V = Vt. Angle θ is defined as the angle between t and the positive direction of x axis. Given that control forces p and q act along the t and n directions, respectively, the equations of motion with respect to the path frame are
![]()
Since the control forces are constant over time interval [ti, ti+1), within this interval the solution for V(t) and θ(t) becomes
where θ0 and V0 are constants of integration and are equal to the values of θ(ti) and V(ti), respectively. By parameterizing the path by the value and direction of the velocity vector, the path can be mapped onto the world frame using the vector integral equation
Here r(t) = (x(t), y(t)) and V = (V · cos(θ), V · sin(θ)) are the projections of vector V onto the world frame (x, y). After integrating Eq. (4.6), we obtain a set of solutions in the form
where terms A and B are

Equations (4.7) are directly defined by the control variables p and q; V(t) and θ(t) therein are given by Eq. (4.5).
In general, Eqs. (4.7) describe a spiral curve. Note two special cases: When p ≠ 0, q = 0, Eqs. (4.7) describe a straight-line motion along the vector of velocity; when p = 0 and q ≠ 0, Eqs. (4.7) produce a circle of radius ![]() centered at the point (A, B).
centered at the point (A, B).
Selection of Control Forces. We now turn to the control law that guides the selection of forces p and q at each step i, for the time interval [ti, ti+1). To ensure a reasonably fast convergence to the intermediate target Ti, those forces are chosen such as to align, as fast as possible, the direction of the robot's motion with the direction toward Ti. First, find a solution among the controls (p, q) such that
where q = +qmax if the intermediate target Ti lies in the left semiplane, and q = −qmax if Ti lies in the right semiplane with respect to the vector of velocity. That is, force p is chosen so as to keep the maximum velocity allowed by the surrounding obstacles. To this end, a discrete set of values p is tried until a step that guarantees a collision-free stopping path is found. At a minimum, the set should include values −pmax, 0, and +pmax. The greater the number of values that are tried, the closer the resulting velocity is to the maximum sought. Force q is chosen on the boundary, to produce a maximum turn in the appropriate direction. On the other hand, if because of obstacles no adequate controls in the range (4.8) can be chosen, this means that maximum braking should be applied. Then the controls are chosen from the set
where q is found from a discrete set similar to p in (4.8). Note that sets (4.8) and (4.9) always include at least one safe solution: By the algorithm design, the straight-line motion with maximum braking, (p, q) = (−pmax, 0), is always collision-free (for more detail, see Ref. 96).
4.2.6 The Algorithm
The resulting algorithm consists of three procedures:
- Main Body. This defines the motion within the time interval [ti, ti+1) toward the intermediate target Ti.
- Define Next Step. This chooses the forces p and q.
- Find Lost Target. This handles the case when the intermediate target goes out of the robot's sight.
Also used in the algorithm is a procedure called Compute Ti, from the VisBug algorithms (Section 3.6), which computes the next intermediate target Ti+1 and includes a test for target reachability. Vector Vi, is the current vector of velocity, and T is the robot's target location. The term “safe motion” below refers to the mechanism for determining the next robot's position Ci+1 such as to guarantee a stopping path (Section 4.2.2).
Main Body. The procedure is executed at each step's time interval [ti, ti+1) and makes use of two procedures, Define Next Step and Find Lost Target (see further below):
- M1: Move in the direction specified by Define Next Step, while executing Compute Ti. If Ti is visible, do the following: If Ci = T, the procedure stops; else if T is unreachable, the procedure stops; else if Ci = Ti, go to M2. Otherwise, use Find Lost Target to make Ti visible. Iterate M1.
- M2: Make a step along vector Vi while executing Compute Ti: If Ci = T, the procedure stops; else if the target is unreachable, the procedure stops; else if Ci ≠ Ti, go to M1.
Define Next Step. This procedure covers all cases of generation of a single motion step. Its part D1 corresponds to motion along the M-line; D2 corresponds to a simple turn when the directions of vectors Vi and (Ci, Ti) can be aligned in one step; D3 is invoked when the turn requires multiple steps and can be done with the maximum speed; D4 is invoked when turning must be accompanied by braking:
- D1: If vector Vi coincides with the direction toward Ti, do the following: If Ti = T, make a step toward T; else make a step toward Ti.
- D2: If vector Vi does not coincide with the direction toward Ti, do the following: If the directions of Vi+1 and (Ci, Ti) can be aligned within one step, choose this step. Else go to D3.
- D3: If a step with the maximum turn toward Ti and with maximum velocity is safe, choose it. Else go to D4.
- D4: If a step with the maximum turn toward Ti and some braking is possible, choose it. Else, choose a step along Vi, with maximum braking, p = −pmax, q = 0.
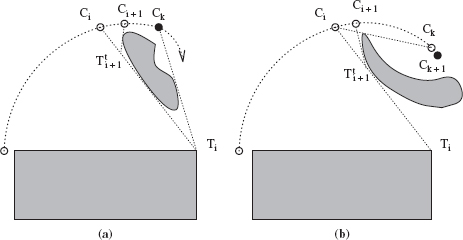
Find Lost Target. This procedure is executed when the intermediate target Ti becomes invisible. The last position Ci where Ti was visible is kept in the memory until Ti becomes visible again. A very simple fix would be this: Once Ti becomes occluded by an obstacle, in order to immediately initiate a stopping path, move back to Ci, and then move directly toward Ti. This would be quite inefficient, however. Instead, the procedure operates as follows: Once the robot loses Ti, it keeps moving ahead while defining temporary intermediate targets on the visible part of the line segment (Ci, Ti), and continuing looking for Ti. If it finds Ti, the procedure terminates, the control returns to the Main Body, and the robot moves directly toward Ti (see Figure 4.6a). Otherwise, if the whole segment (Ci, Ti) becomes invisible, the robot brakes to a stop, returns to Ci, the procedure terminates, and so on (see Figure 4.6b). Together these two pieces ensure that the intermediate target Ti will not be lost. The procedure is as follows:
- F1: If segment (Ci, Ti) is visible, define on it a temporary intermediate target
 and move toward it while looking for Ti. If the current position is at T, exit; else if Ci lies in the segment (Ci, Ti), exit. Else go to F2.
and move toward it while looking for Ti. If the current position is at T, exit; else if Ci lies in the segment (Ci, Ti), exit. Else go to F2. - F2: If segment (Ci, Ti) is invisible, initiate a stopping path and move back to Ci; exit.
Figure 4.6 Because of its inertia, immediately after its position Ci the robot temporarily “loses” the target intermediate Ti. (a) The robot keeps moving around the obstacle until it spots Ti, and then it continues toward Ti. (b) When because of an obstacle the whole segment (Ci, Ti) becomes invisible at point Ck+1, the robot stops, returns back to Ci, and then moves toward Ti along the line (Ci, Ti).
Convergence. To prove convergence of the described procedure, we need to show the following:
(i) At every step of the path the algorithm guarantees collision-free motion.
(ii) The set of intermediate targets Ti is guaranteed to lie on the convergent path.
(iii) The planning strategy guarantees that the current intermediate target will not be lost.
Together, (ii) and (iii) assure that a path to the target position T will be found if one exists. Condition (i) can be shown by induction; condition (ii) is provided by the VisBug procedure (see Section 3.6), which also includes the test for target reachability. Condition (iii) is satisfied by the procedure Find Lost Target of the Maximum Turn Strategy. The following two propositions hold:
Proposition 2. Under the Maximum Turn Strategy algorithm, assuming zero velocity, VS = 0, at the start position S, at each step of the path there exists at least one stopping path.
By design, the stopping path is a straight-line segment. Choosing the next step so as to guarantee existence of a stopping path implies two requirements: There should be at least one safe direction of motion and the value of velocity that would allow stopping within the visible area. The latter is ensured by the choice of system parameters [see Eq. (4.1) and the safety conditions, Section 4.2.2]. As to the existence of safe directions, proceed by induction: We need to show that if a safe direction exists at the start point and at an arbitrary step i, then there is a safe direction at the step (i + 1).
Since at the start point S the velocity is zero, Vs = 0, then any direction of motion at S will be a safe direction; this gives the basis of induction. The induction proceeds as follows. Under the algorithm, a candidate step is accepted for execution if only its direction guarantees a safe stop for the robot if needed. Namely, at point Ci, step i is executed only if the resulting vector Vi+1 at Ci+1 will point in a safe direction. Therefore, at step (i + 1), at the least this very direction presents a safe stopping path.
Remark: Proposition 2 will hold for VS ≠ 0 as well if the start point S is known to possess at least one stopping path originating in it.
Proposition 3. The Maximum Turn Strategy is convergent.
To see this, note that by design of the VisBug algorithm (see Section 3.6.3), each intermediate target Ti lies on a convergent path and is visible at the moment when it is generated.
That is, the only way the robot can get lost is if at the following step(s) point Ti becomes invisible due to the robot's inertia or an obstacle occlusion: This would make it impossible to generate the next intermediate target, Ti+1, as required by VisBug. However, if point Ti does become invisible, the procedure Find Lost Target is invoked, a set of temporary intermediate targets ![]() are defined, each with a guaranteed stopping path, and more steps are executed until point Ti becomes visible again (see Figure 4.6). The set
are defined, each with a guaranteed stopping path, and more steps are executed until point Ti becomes visible again (see Figure 4.6). The set ![]() is finite because of finite distances between every pair of points in it and because the set must lie within the sensing range of radius rυ. Therefore, the robot always moves toward a point which lies on a path that is convergent to the target T.
is finite because of finite distances between every pair of points in it and because the set must lie within the sensing range of radius rυ. Therefore, the robot always moves toward a point which lies on a path that is convergent to the target T.
4.2.7 Examples
Examples shown in Figures 4.7a to 4.7d demonstrate performance of the Maximum Turn Strategy in a computer simulated environment. Generated paths are shown by thicker lines. For comparison, also shown by thin lines are paths produced under the same conditions by the VisBug algorithm. Polygonal shapes are chosen for obstacles in the examples only for the convenience of generating the scene; the algorithms are oblivious to the obstacle shapes.
To understand the examples, consider a simplified version of the relationship that appears in Section 4.2.3, ![]() . In the simulations, the robot's mass m and control force fmax are kept constant; for example, an increase in sensing radius rυ would “raise” the velocity Vmax. Radius rυ is the same in Figures 4.7a and 4.7b. In the more complex scene (b), because of three additional obstacles (three small squares) the robot's path cannot curve as freely as in scene (a). Consequently, the robot moves more “cautiously,” that is, slower; the path becomes tighter and closer to the obstacles, allowing the robot to squeeze between obstacles. Accordingly, the time to complete the path is 221 units (steps) in (a) and 232 units in (b), whereas the path in (a) is longer than that in (b).
. In the simulations, the robot's mass m and control force fmax are kept constant; for example, an increase in sensing radius rυ would “raise” the velocity Vmax. Radius rυ is the same in Figures 4.7a and 4.7b. In the more complex scene (b), because of three additional obstacles (three small squares) the robot's path cannot curve as freely as in scene (a). Consequently, the robot moves more “cautiously,” that is, slower; the path becomes tighter and closer to the obstacles, allowing the robot to squeeze between obstacles. Accordingly, the time to complete the path is 221 units (steps) in (a) and 232 units in (b), whereas the path in (a) is longer than that in (b).
Figure 4.7 In each of the four examples shown, one path (indicated by the thin line) is produced by the VisBug algorithm, and the other path (a thicker line) is produced by the Maximum Turn Strategy, which takes into account the robot dynamics. The circle at point S indicates the radius of vision rυ.
Figures 4.7c and 4.7d refer to a more complex environment. The difference between these two situations is that in (d) the radius of vision rυ is 1.5 times larger than that in (c). Note that in (d) the path produced by the Maximum Turn Strategy is noticeably shorter than the path generated by the VisBug algorithm. This has happened by sheer chance: Unable to make a sharp turn (because of its inertia) at the last piece of its path, the robot “jumped out” around the corner and hence happened to be close enough to T to see it, and this eliminated a need for more obstacle following.
Note the stops along the path generated by the Maximum Turn Strategy; they are indicated by sharp turns. These might have been caused by various reasons: For example, in Figure 4.7a the robot stopped because its small sensing radius rυ was insufficient to see the obstacle far enough to initiate a smooth turn. In Figure 4.7d, the stop at point P was probably caused by the robot's temporarily losing its current intermediate target.
4.3 MINIMUM TIME STRATEGY
We will now consider the second strategy for solving the Jogger's Problem. The same model of the robot, its environment, and its control means will be used as in the Maximum Turn Strategy (see Section 4.2.1).
The general strategy will be as follows: At the given step i, the kinematic motion planning procedure chosen—we will use again VisBug algorithms— identifies an intermediate target point, Ti, which is the farthest visible point on a convergent path. Normally, though not always, Ti is defined at the boundary of the sensing range rυ. Then a single step that lies on a time-optimal trajectory to Ti is calculated and executed; the robot moves from its current position Ci to the next position Ci+1, and the process repeats.
Similar to the Maximum Turn Strategy, the fact that no information is available beyond the robot's sensing range dictates a number of requirements. There must be an emergency stopping path, and it must lie inside the current sensing area. Since parts of the sensing range may be occupied or occluded by obstacles, the stopping path must lie in its visible part. Next, the robot needs a guarantee of stopping at the intermediate target Ti, even if it does not intend to do so. That is, each step is to be planned as the first step of a trajectory which, given the robot's current position, velocity, and control constraints, would bring it to a halt at Ti (though, again, this will be happening only rarely).
The step-planning task is formulated as an optimization problem. It is the optimization criterion and procedure that will make this algorithm quite different from the Maximum Turn Strategy. At each step, a canonical solution is found which, if no obstacles are present, would bring the robot from its current position Ci to its current intermediate target Ti with zero velocity and in minimum time. If the canonical path happens to be infeasible because it crosses an obstacle, a collision-free near-canonical solution path is found. We will show that in this case only a small number of path options need be considered, at least one of which is guaranteed to be collision-free.
By making use of the L∞-norm within the duration of a single step, we decouple the two-dimensional problem into two one-dimensional control problems and reduce the task to the bang-bang control strategy. This results in an extremely fast procedure for finding the time-optimal subpath within the sensing range. The procedure is easily implementable in real time. Since only the first step of this subpath is actually executed—the following step will be calculated when new sensor information appears after this (first) step is executed—this decreases the error due to the control decoupling. Then the process repeats. One special case will have to be analyzed and incorporated into the procedure—the case when the intermediate target goes out of the robot's sight either because of the robot inertia or because of occluding obstacles.
4.3.1 The Model
To a large extent the model that we will use in this section is similar to the model used by the Maximum Turn Strategy above. There are also some differences. For convenience we hence give a complete model description here.
As before, the scene is two-dimensional physical space ![]() it may include a finite set of locally finite static obstacles
it may include a finite set of locally finite static obstacles ![]() . Each obstacle
. Each obstacle ![]() is a simple closed curve of arbitrary shape and of finite length, such that a straight line will cross it in only a finite number of points. Obstacles do not touch each other; if they do, they are considered one obstacle.
is a simple closed curve of arbitrary shape and of finite length, such that a straight line will cross it in only a finite number of points. Obstacles do not touch each other; if they do, they are considered one obstacle.
The robot is a point mass, of mass m. Its vision sensor allows it to detect any obstacles and the distance to them within its sensing range (radius of vision)—a disk D(Ci, rυ) of radius rυ centered at its current location Ci. At moment ti, the robot's input information includes its current velocity vector Vi and coordinates of Ci and of target location T.
The robot's means to control its motion are two components of the acceleration vector u = f/m = (p, q), where m is the robot mass and f the force applied. Controls u come from a set u(·) ∈ U of measurable, piecewise continuous bounded functions in ℜ2, U = {u(·) = (p(·), q(·))/p ∈ [−pmax, pmax], q ∈ [−qmax, qmax]}. By taking mass m = 1, we can refer to components p and q as control forces, each within a fixed range |p| ≤ pmax, |q| ≤ qmax; pmax, qmax > 0. Force p controls the forward (or backward when braking) motion; its positive direction coincides with the robot's velocity vector V. Force q, the steering control, is perpendicular to p, forming a right pair of vectors (Figure 4.8). There is no friction: For example, given velocity V, the control values p = q = 0 will result in a constant-velocity straight-line motion along the vector V.
Without loss of generality, assume that no external forces except p and q act on the system. Note that with this assumption our model and approach can still handle other external forces and constraints using, for example, the technique suggested in Ref. 95, whereby various dynamic constraints such as curvature, engine force, sliding, and velocity appear in the inequality describing the limitations on the components of acceleration. The set of such inequalities defines a convex region of the ![]() space. In our case the control forces act within the intersection of the box [−pmax, pmax] × [−qmax, qmax], with the half-planes defined by those inequalities.
space. In our case the control forces act within the intersection of the box [−pmax, pmax] × [−qmax, qmax], with the half-planes defined by those inequalities.
The task is to move in ![]() from point S (start) to point T (target) (see Figure 4.1). The control of robot motion is done in steps i, i = 0, 1, 2,… Each step i takes time δt = ti+1 − ti = const; the path length within time interval δt depends on the robot velocity Vi. Steps i and i + 1 start at times tt and ti+1, respectively; C0 = S. Control forces u(·) = (p, q) ∈ U are constant within the step.
from point S (start) to point T (target) (see Figure 4.1). The control of robot motion is done in steps i, i = 0, 1, 2,… Each step i takes time δt = ti+1 − ti = const; the path length within time interval δt depends on the robot velocity Vi. Steps i and i + 1 start at times tt and ti+1, respectively; C0 = S. Control forces u(·) = (p, q) ∈ U are constant within the step.
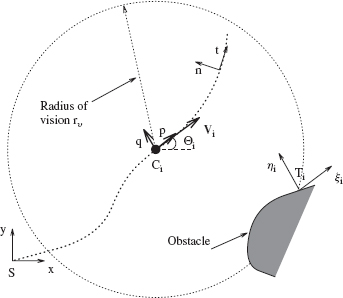
We define three coordinate systems (follow Figure 4.8):
- The world frame, (x, y), is fixed at point S.
- The primary path frame, (t, n), is a moving (inertial) coordinate frame. Its origin is attached to the robot; axis t is aligned with the current velocity vector V, axis n is normal to t. Together with axis b, which is a cross product b = t × n, the triple (t, n, b) forms the Frenet trihedron, with the plane of t and n forming the osculating plane [97].
- The secondary path frame, (ξi, ηi), is a coordinate frame that is fixed during the time interval of step i. The frame's origin is at the intermediate target Ti; axis ξi is aligned with the velocity vector Vi at time ti, and axis ηi is normal to ξi.
For convenience we combine the requirements and constraints that affect the control strategy into a set, called Ω. A solution (a path, a step, or a set of control values) is said to be Ω-acceptable if, given the current position Ci and velocity Vi,
(i) it satisfies the constraints |p| ≤ pmax, |q| ≤ qmax on the control forces,
(ii) it guarantees a stopping path,
(iii) it results in a collision-free motion.
4.3.2 Sketching the Approach
The algorithm that we will now present is executed at each step of the robot path. The procedure combines the convergence mechanism of a kinematic sensor-based motion planning algorithm with a control mechanism for handling dynamics, resulting in a single operation. As in the previous section, during the step time interval i the robot will maintain within its sensing range an intermediate target point Ti, usually on an obstacle boundary or on the desired path. At its current position Ci the robot will plan and execute its next step toward Ti. Then at Ci+1 it will analyze new sensory data and define a new intermediate target Ti+1, and so on. At times the current Ti may go out of the robot's sight because of its inertia or due to occluding obstacles. In such cases the robot will rely on temporary intermediate targets until it can locate point Ti again.
The Kinematic Part. In principle, any maze-searching procedure can be utilized here, so long as it allows an extension to distant sensing. For the sake of specificity, we use here a VisBug algorithm (see Section 3.6; either VisBug-21 or VisBug-22 will do). Below, M-line (Main line) is the straight-line connecting points S and T; it is the robot's desired path. When, while moving along the M-line, the robot encounters an obstacle, the M-line, the intersection point between M-line and the obstacle boundary is called a hit point, denoted as H. The corresponding complementary intersection point between the M-line and the obstacle “on the other side” of the obstacle is a leave point, denoted L. Roughly, the algorithm revolves around two steps (see Figure 4.1):
- Walk from S toward T along the M-line until detect an obstacle crossing the M-line, say at point H. Go to Step 2.
- Define a farthest visible intermediate target Ti on the obstacle boundary in the direction of motion; make a step toward Ti. Iterate Step 2 until detect M-line. Go to Step 1.
The actual algorithm will include additional mechanisms, such as a finite-time target reachability test and local path optimization. In the example shown in Figure 4.1, note that if the robot walked under a kinematic algorithm, at point P it would make a sharp turn (recall that the algorithm assumes holonomic motion). In our case, however, such motion is not possible because of the robot inertia, and so the actual motion beyond point P would be something closer to the dotted path.
The Effect of Dynamics. Dynamics affects three algorithmic issues: safety considerations, step planning, and convergence. Consider those separately.
Safety Considerations. Safety considerations refer to collision-free motion. The robot is not supposed to hit obstacles. Safety considerations appear in a number of ways. Since at the robot's current position no information about the scene is available beyond the distance rυ from it, guaranteeing collision-free motion means guaranteeing at any moment at least one “last resort” stopping path. Otherwise in the following steps new obstacles may appear in the sensing range, and collision will be imminent no matter what control is used. This dictates a certain relationship between the velocity V, mass m, radius rυ, and controls u = (p, q). Under a straight-line motion, the range of safe velocities must satisfy
where d is the distance from the robot to the stop point. That is, if the robot moves with the maximum velocity, the stop point of the stopping path must be no further than rυ from the current position C. In practice, Eq. (4.10) can be interpreted in a number of ways. Note that the maximum velocity is proportional to the acceleration due to control, which is in turn directly proportional to the force applied and inversely proportional to the robot mass m. For example, if mass m is made larger and other parameters stay the same, the maximum velocity will decrease. Conversely, if the limits on (p, q) increase (say, due to more powerful motors), the maximum velocity will increase as well. Or, an increase in the radius rυ (say, due to better sensors) will allow the robot to increase its maximum velocity, by the virtue of utilizing more information about the environment.
Consider the example in Figure 4.1. When approaching point P along its path, the robot will see it at distance rυ and will designate it as its next intermediate target Ti. Along this path segment, point Ti happens to stay at P because no further point on the obstacle boundary will be visible until the robot arrives at P. Though there may be an obstacle right around the corner P, the robot needs not to slow down since at any point of this segment there is a possibility of a stopping path ending somewhere around point Q. That is, in order to proceed with maximum velocity, the availability of a stopping path has to be ascertained at every step i. Our stopping path will be a straight-line path along the corresponding vector Vi. If a candidate step cannot guarantee a stopping path, it is discarded.4
Step Planning. Normally the stopping path is not used; it is only an “insurance” option. The actual step is based on the canonical solution, a path which, if fully executed, would bring the robot from Ci to Ti with zero velocity and in minimum time, assuming no obstacles. The optimization problem is set up based on Pontryagin's optimality principle. We assume that within a step time interval [ti, ti+1) the system's controls (p, q) are bounded in the L∞-norm, and apply it with respect to the secondary coordinate frame (ξi, ηi). The result is a fast computational scheme easily implementable in real time. Of course only the very first step of the canonical path is explicitly calculated and used in the actual motion. At the next step, a new solution is calculated based on the new sensory information that arrived during the previous step, and so on. With such a step-by-step execution of the optimization scheme, a good approximation of the globally time-optimal path from Ci to Ti is achieved. On the other hand, little computation is wasted on the part of the path solution that will not be utilized.
If the step suggested by the canonical solution is not feasible due to obstacles, a close approximation, called the near-canonical solution, is found that is both feasible and Ω-acceptable. For this case we show, first, that only a finite number of path options need be considered and, second, that there exists at least one path solution that is Ω-acceptable. A special case here is when the intermediate target goes out of the robot's sight either because of the robot's inertia or because of occluding obstacles.
Convergence. Once a step is physically executed, new sensing information appears and the process repeats. If an obstacle suddenly appears on the robot's intended path, a detour is arranged, which may or may not require the robot to stop. The detour procedure is tied to the issue of convergence, and it is built similar to the case of normal motion. Because of the effect of dynamics, the convergence mechanism borrowed from a kinematic algorithm—here VisBug—will need some modification. The intermediate target points Ti produced by VisBug lie either on the boundaries of obstacles or on the M-line, and they are visible from the corresponding robot's positions.
However, the robot's inertia may cause it to move so that Ti will become invisible, either because it goes outside of the sensing range rυ (as after point P, Figure 4.1) or due to occluding obstacles (as in Figure 4.11). This may endanger path convergence. A safe but inefficient solution would be to slow down or to keep the speed small at all times to avoid such overshoots. The solution chosen (Section 4.3.6) is to keep the velocity high and, if the intermediate target Ti goes out of sight, modify the motion locally until Ti is found again.
4.3.3 Dynamics and Collision Avoidance
Consider a time sequence σt = {t0, t1, t2, …, } of the starting moments of steps. Step i takes place within the interval [ti, ti+1), (ti+1 − ti) = δt. At moment ti the robot is at the position Ci, with the velocity vector Vi. Within this interval, based on the sensing data, intermediate target Ti (supplied by the kinematic planning algorithm), and vector Vi, the control system will calculate the values of control forces p and q. The forces are then applied to the robot, and the robot executes step i, finishing it at point Ci+1 at moment ti+1, with the velocity vector Vi+1. Then the process repeats.
Analysis that leads to the procedure for handling dynamics consists of three parts. First, in the remainder of this section we incorporate the control constraints into the robot's model and develop transformations between the primary path frame and world frame and between the secondary path frame and world frame. Then in Section 4.3.4 we develop the canonical solution. Finally, in Section 4.3.5 we develop the near-canonical solution, for the case when the canonical solution would result in a collision. The resulting algorithm operates incrementally; forces p and q are computed at each step. The remainder of this section refers to the time interval [ti, ti+1) and its intermediate target Ti, and so index i is often dropped.
Denote (x, y) ∈ ℜ2 the robot's position in the world frame, and denote θ the (slope) angle between the velocity vector ![]() and x axis of the world frame (Figure 4.8). The planning process involves computation of the controls u = (p, q), which for every step define the velocity vector and eventually the path, (x(t), y(t)), as a function of time. Taking mass m = 1, the equations of motion become
and x axis of the world frame (Figure 4.8). The planning process involves computation of the controls u = (p, q), which for every step define the velocity vector and eventually the path, (x(t), y(t)), as a function of time. Taking mass m = 1, the equations of motion become
Figure 4.8 The coordinate frame (x, y) is the world frame, with its origin at S; (t, n) is the primary path frame, and (ξi, ηi) is the secondary path frame for the current robot position Ci.
![]()
The angle θ between vector V = (Vx, Vy) and x axis of the world frame is found as

The transformations between the world frame and secondary path frame, from (x, y) to (ξ, η) and from (ξ, η) to (x, y), are given by
and
where
![]()
R′ is the transpose matrix of the rotation matrix between the frames (ξ, η) and (x, y), and (xT, yT) are the coordinates of the (intermediate) target in the world frame (x, y).
To define the transformations between the world frame (x, y) and the primary path frame (t, n), write the velocity in the primary path frame as V = Vt. To find the time derivative of vector V with respect to the world frame (x, y), note that the time derivative of vector t in the primary path frame (see Section 4.3.1) is not equal to zero. It can be defined as the cross product of angular velocity ![]() of the primary path frame and vector t itself:
of the primary path frame and vector t itself: ![]() , where angle θ is between the unit vector t and the positive direction of x axis. Given that the control forces p and q act along the t and n directions, respectively, the equations of motion with respect to the primary path frame are
, where angle θ is between the unit vector t and the positive direction of x axis. Given that the control forces p and q act along the t and n directions, respectively, the equations of motion with respect to the primary path frame are
![]()
Since p and q are constant over the time interval t ∈ [ti, ti+1), the solution for V(t) and θ(t) within the interval becomes
where θ0 and V0 are constants of integration and are equal to the values of θ(ti) and V(ti), respectively. By parameterizing the path by the value and direction of the velocity vector, the path can be mapped into the world frame (x, y) using the vector integral equation
Here r(t) = (x(t), y(t)), and t is a unit vector of direction V, with the projections t = (cos(θ), sin(,θ)) onto the world frame (x, y). After integrating Eq. (4.14), obtain the set of solutions
where terms A and B are

and V(t) and θ(t) are given by (4.13).
Equations (4.15) describe a spiral curve. Note two special cases: When p ≠ 0 and q = 0, Eqs. (4.15) describe a straight-line motion under the force along the vector of velocity; when p = 0 and q ≠ 0, the force acts perpendicular to the vector of velocity, and Eqs. (4.15) produce a circle of radius ![]() centered at the point (A, B).
centered at the point (A, B).
4.3.4 Canonical Solution
Given the current position Ci = (xi, yi), the intermediate target Ti, and the velocity vector ![]() , the canonical solution presents a path that, assuming no obstacles, would bring the robot from Ci to Ti with zero velocity and in minimum time. The L∞-norm assumption allows us to decouple the bounds on accelerations in ξ and η directions, and thus treat the two-dimensional problem as a set of two one-dimensional problems, one for control p and the other for control q. For details on obtaining such a solution and the proof of its sufficiency, refer to Ref. 99.
, the canonical solution presents a path that, assuming no obstacles, would bring the robot from Ci to Ti with zero velocity and in minimum time. The L∞-norm assumption allows us to decouple the bounds on accelerations in ξ and η directions, and thus treat the two-dimensional problem as a set of two one-dimensional problems, one for control p and the other for control q. For details on obtaining such a solution and the proof of its sufficiency, refer to Ref. 99.
The optimization problem is formulated based on the Pontryagin's optimality principle [100], with respect to the secondary frame (ξ, η). We seek to optimize a criterion F, which signifies time. Assume that the trajectory being sought starts at time t = 0 and ends at time t = tf (for “final”). Then, the problem at hand is
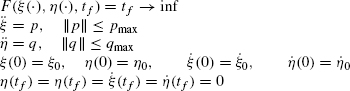
Analysis shows (see details in the Appendix in Ref. 99) that the optimal solution of each one-dimensional problem corresponds to the “bang-bang” control, with at most one switching along each of the directions ξ and η, at times ts,ξ and ts,η (“s” stands for “switch”), respectively.
The switch curves for control switchings are two connected parabolas in the phase space ![]() ,
,
and in the phase space ![]() , respectively (see Figure 4.9),
, respectively (see Figure 4.9),
The time-optimal solution is then obtained using the bang-bang strategy for ξ and η, depending on whether the starting points, ![]() and
and ![]() , are above or below their corresponding switch curves, as follows:
, are above or below their corresponding switch curves, as follows:
where α1 = −1, α2 = 1 if the starting point, ![]() s or
s or ![]() s, respectively, is above its switch curves, and α1 = 1, α2 = −1 if the starting point is below its switch curves. For example, if the initial conditions for ξ and η are as shown in Figure 4.9, then
s, respectively, is above its switch curves, and α1 = 1, α2 = −1 if the starting point is below its switch curves. For example, if the initial conditions for ξ and η are as shown in Figure 4.9, then
Figure 4.9 (a) The start position in the phase space ![]() is above the switch curves. (b) The start position in the phase space
is above the switch curves. (b) The start position in the phase space ![]() is under the switch curves.
is under the switch curves.
where the caret sign (ˆ) refers to the parameters under optimal control. The time, position, and velocity of the control switching for the ξ components are described by
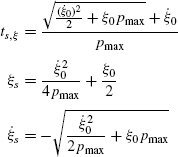
and those for the η components are described by

The number, time, and locations of switchings can be uniquely defined from the initial and final conditions. It can be shown (see Appendix in Ref. 99) that for every position of the robot in the ℜ4 ![]() the control law obtained guarantees time-optimal motion in both ξ and η directions, as long as the time interval considered is sufficiently small. Substituting this control law in the equations of motion (4.15) produces the canonical solution.
the control law obtained guarantees time-optimal motion in both ξ and η directions, as long as the time interval considered is sufficiently small. Substituting this control law in the equations of motion (4.15) produces the canonical solution.
To summarize, the procedure for obtaining the first step of the canonical solution is as follows:
- Substitute the current position/velocity
 into the equations (4.16) and (4.17) and see if the starting point is above or below the switch curves.
into the equations (4.16) and (4.17) and see if the starting point is above or below the switch curves. - Depending on the above/below information, take one of the four possible bang-bang control pairs p, q from (4.18).
- With this pair (p, q), find from (4.15) the position Ci+1 and from (4.13) the velocity Vi+1 and angle θi+1 at the end of the step. If this step to Ci+1 crosses no obstacles and if there exists a stopping path in the direction Vi+1, the step is accepted; otherwise, a near-canonical solution is sought (Section 4.3.5).
Note that though the canonical solution defines a fairly complex multistep path from Ci to Ti, only one—the very first—step of that path is calculated explicitly. The switch curves (4.16) and (4.17), as well as the position and velocity equations (4.15) and (4.13), are quite simple. The whole computation is therefore very fast.
4.3.5 Near-Canonical Solution
As discussed above, unless a step that is being considered for the next moment guarantees a stopping path along its velocity vector, it will be rejected. This step will be always the very first step of the canonical solution. If the stopping path of the candidate step happens to cross an obstacle within the distance found from (4.10), the controls are modified into a near-canonical solution that is both Ω-acceptable and reasonably close to the canonical solution. The near-canonical solution is one of the nine possible combinations of the bang-bang control pairs (k1 · pmax, k2 · qmax), where k1 and k2 are chosen from the set {− 1, 0, 1} (see Figure 4.10).
Since the canonical solution takes one of those nine control pairs, the near-canonical solution is to be chosen from the remaining eight pairs. This set is guaranteed to contain an Ω-acceptable solution: Since the current position has been chosen so as to guarantee a stopping path, this means that if everything else fails, there is always the last resort path back to the current position—for example, under control (−pmax, 0).
Figure 4.10 Near-canonical solution. Controls (p, q) are assumed to be L∞-norm bounded on the small interval of time. The choice of (p, q) is among the eight “bang-bang” solutions shown.
Furthermore, the position of the intermediate target Ti relative to vector Vi—in its left or right semiplane—suggests an ordered and thus shorter search among the control pairs. For step i, denote the nine control pairs ![]() , j = 0, 1, 2, … , 8, as shown in Figure 4.10. If, for example, the canonical solution is
, j = 0, 1, 2, … , 8, as shown in Figure 4.10. If, for example, the canonical solution is ![]() , then the near-canonical solution will be the first Ω-acceptable control pair uj = (p, q) from the sequence (u3, u1, u4, u0, u8, u5, u7, u6). Note that u5 is always Ω-acceptable.
, then the near-canonical solution will be the first Ω-acceptable control pair uj = (p, q) from the sequence (u3, u1, u4, u0, u8, u5, u7, u6). Note that u5 is always Ω-acceptable.
4.3.6 The Algorithm
The complete motion planning algorithm is executed at every step of the path, and it generates motion by computing canonical or near-canonical solutions at each step. It includes four procedures:
(i) The Main Body procedure monitors the general control of motion toward the intermediate target Ti. In turn, Main Body makes use of three procedures:
(ii) Procedure Define Next Step chooses the controls (p, q) for the next step.
(iii) Procedure Find Lost Target deals with the special case when the intermediate target Ti goes out of the robot's sight.
(iv) Main Body also uses the procedure called Compute Ti, taken directly from the kinematic algorithm (for example, VisBug-21 or VisBug-22, Section 3.6), which computes the next intermediate target Ti+1 so as to guarantee the global convergence, and also performs the test for target reachability.
As before, S is the starting point, T—the robot target position; at step i, Ci is the robot's current position, vector Vi—the current velocity vector. Initially, i = 0, Ci = Ti = S.
Procedure Main Body. At each step i:
- If Ci = T, stop.
- Find Ti from Compute Ti.
- If T is found unreachable, stop.
- If Ti is visible, find Ci+1 from Define Next Step; make a step toward Ci+1; iterate; else,
- Use Find Lost Target to produce Ti visible; iterate.
Procedure Define Next Step. This procedure consists of two steps:
S1: Find the canonical solution (the switch curves and controls (p, q)) using Eqs. (4.16), (4.17), and (4.18). If it is Ω-acceptable, exit; else go to S2.
S2: Find the near-canonical solution as in Section 4.3.5; exit.
Procedure Find Lost Target. This procedure is executed when Ti becomes invisible. The last position Ci where Ti was visible is then stored until Ti becomes visible again. Various heuristics can be used here as long as convergence is preserved. One simple strategy would be to come to a halt using a stopping path, then come back to Ci with zero velocity, and then move directly toward Ti. This may add stops that could be avoided. The procedure chosen below is somewhat smarter in that the robot does not stop unnecessarily: If the robot loses Ti, it keeps moving ahead while defining temporary intermediate targets ![]() on the visible part of the line segment (Ci, Ti) and continues looking for Ti. If it locates Ti, it turns directly toward it without stopping (Figure 4.11a). Otherwise, if the whole segment (Ci, Ti) becomes invisible, the robot brakes to a stop, returns to Ci with zero velocity, and then moves directly toward Ti (Figure 4.11b). Find Lost Target operates as follows:
on the visible part of the line segment (Ci, Ti) and continues looking for Ti. If it locates Ti, it turns directly toward it without stopping (Figure 4.11a). Otherwise, if the whole segment (Ci, Ti) becomes invisible, the robot brakes to a stop, returns to Ci with zero velocity, and then moves directly toward Ti (Figure 4.11b). Find Lost Target operates as follows:
S1: While at Ck, k > i, find on the segment (Ci, Ti) the visible point closest to Ti; denote it ![]() . If there is no such point [i.e., the whole segment (Ci, Ti) is not visible], go to S2. Else, using Define Next Step, compute and execute the next step using
. If there is no such point [i.e., the whole segment (Ci, Ti) is not visible], go to S2. Else, using Define Next Step, compute and execute the next step using ![]() as the temporary intermediate target; iterate.
as the temporary intermediate target; iterate.
S2: Initiate a stopping path, then go back to Ci; exit.
Figure 4.11 In these examples, because of the system inertia the robot temporarily “loses” the intermediate target point Ti. (a) The robot keeps moving forward until at Ck it sees Ti. (b) At Ck the robot initiates a stopping path, stops at Ck+1, returns back to Ci, and moves toward Ti along the line (Ci, Ti).
4.3.7 Convergence. Computational Complexity
Convergence. The collision-free motion along the path is guaranteed by the design of the canonical and near-canonical solutions. To prove convergence, we need to show that the algorithm will find a path to the target position T if one exists, or will infer in finite time that T is not reachable if true. This is guaranteed by the convergence properties of the kinematic algorithm (Section 3.6). The following two statements, Claim 1 and Claim 2, hold:
Claim 1. Under the Minimum Time Strategy, assuming zero velocity VS = 0 at the starting position S, at each step of the path there exists at least one stopping path.
To see this, recall that according to our model the stopping path lies along a straight line. Guaranteeing a stopping path implies two requirements: a safe direction and the velocity value that will allow a stop within the visible area. Because the latter is ensured by the choice of the system parameters in (4.10), we focus now on the existence of safe directions. Proceed by induction: We have to show that if a safe direction exists at the start point and on an arbitrary step i, then there is a safe direction on the step (i + 1).
Since at the start point S the velocity is zero, any direction of motion at S will be a safe direction. This gives the basis of induction. The induction step is as follows. Under the algorithm, a candidate step is accepted for execution only if its direction guarantees a safe stop for the robot if needed. Namely, at point Ci, step i is executed only if the resulting vector Vi+1 at Ci+1 will point in a safe direction. Therefore, at step (i + 1), at the least this very direction can be used for a stopping path.
Remark: Claim 1 will hold for VS ≠ 0 as well if there exists at least one stopping path originating at the start point S.
In practical terms, this is a reasonable condition. If for some reason the robot did not start at S and was passing through it on the fly—which is already strange enough—it is hard to imagine that point S happened to be so bad that it could not even provide a stopping path.
Claim 2. The Minimum Time Strategy guarantees convergence.
To see this, note that at each step i at its current position Ci, the robot uses its sensing to generate the next intermediate target point Ti. That point Ti is known to lie on a convergent path of the kinematic algorithm (Section 3.6.3). At the moment when Ti is generated, it is visible. Hence, the only way that the robot can get lost is if at the next step Ci+1 point Ti becomes invisible due to the robot inertia or obstacle occlusion: This would make it impossible to generate the intermediate target Ti+1 as required by the kinematic algorithm. But, if indeed point Ti becomes invisible, the Find Lost Target procedure is invoked and a set of temporary intermediate targets ![]() and associated steps are executed until point Ti becomes visible again (see Figure 4.11a). Thus the robot always moves toward a point that lies on a convergent path and itself converges to the target T.
and associated steps are executed until point Ti becomes visible again (see Figure 4.11a). Thus the robot always moves toward a point that lies on a convergent path and itself converges to the target T.
Computational Complexity. As with other on-line sensor-based algorithms, it would not be very informative to try to assess the algorithm complexity the way it is usually done for algorithms with complete information, as a function of the number of vertices of approximated obstacles (see Chapter 1). As one reason, algorithms with complete information deal with one-time computation, whereas in sensor-based algorithms the important complexity measure is the amount of computations at each step; the total computation time is simply a linear function of the path length.
As shown in Section 4.3.4, though the canonical solution found by the algorithm at each path step is the solution of a fairly complex time-optimal problem, its computational cost is remarkably low, thanks to the (optimal) bang-bang control. This computation includes (a) substituting the initial conditions ![]() into the equations for parabolas [Eqs. (4.16) and (4.17)] to see if the start point is above or below the corresponding parabola and (b) simply taking the corresponding control pair
into the equations for parabolas [Eqs. (4.16) and (4.17)] to see if the start point is above or below the corresponding parabola and (b) simply taking the corresponding control pair ![]() from the four choices in (4.18). The parabola equations themselves are found beforehand, only once. The near-canonical solution, when needed, is similar and as fast. Note that a single-step computation is of constant time: Though the canonical solution represents the whole multistep trajectory within the sensing range of radius rυ, the computation time is independent of the value rυ and of the length of path within the sensing range.
from the four choices in (4.18). The parabola equations themselves are found beforehand, only once. The near-canonical solution, when needed, is similar and as fast. Note that a single-step computation is of constant time: Though the canonical solution represents the whole multistep trajectory within the sensing range of radius rυ, the computation time is independent of the value rυ and of the length of path within the sensing range.
Figure 4.12 Examples of performance of the Minimum Time Strategy. Parts (a) and (b) differ in that more obstacles are added in (b). Parts (c) and (d) relate to the same scenes, respectively, and have a larger radius of vision rυ. The radius of vision in (f) is significantly larger than that in (e). Note the stopping points along the paths.
4.3.8 Examples
The performance of Minimum Time Strategy algorithm is illustrated in Figure 4.12. The examples shown are computer simulations. The robot mass m and constraints on control parameters p and q are the same for all examples: pmax = qmax, pmax/m = 1. The generated paths are shown in thicker lines. For the purpose of comparison, also shown (in a thin line) are paths produced under the same conditions by a kinematic algorithm VisBug.
The radius of vision rυ is the same in both Figures 4.12a and 4.12b. The difference is in the environment: In Figure 4.12b there are additional obstacles; that is, the robot suddenly uncovers them at a close distance when turning around a corner. Note that in Figure 4.12b the path becomes tighter and shorter, though it takes longer: Measured in the number of steps, the path in Figure 4.12a takes 242 steps, and the path in Figure 4.12b takes 278 steps. One can say the robot becomes more cautious in Figure 4.12b.
A similar pair of examples shown in Figures 4.12c and 4.12d illustrates the effect of the radius of vision rυ : Here it is twice as big as the radius of vision in Figures 4.12a and 4.12b. The times to execute the path here are 214 and 244 steps, respectively, shorter than in the corresponding examples in Figures 4.12a and 4.12b. The examples thus demonstrate that better sensing (larger rυ) results in shorter time to complete the task: More crowded space results in longer time, though possibly in shorter paths.
Note that in some points the algorithm found it necessary to make use of the stopping path; those points are usually easy to recognize from the sharp turns in the path. For example, in Figure 4.12a the robot came to a halt at points A and D, and in Figure 4.12b it stopped at points A–F. The algorithm's performance in a more complicated environment is shown in Figures 4.12e and 4.12f. In Figure 4.12f the radius of vision rυ is significantly larger than that in Figure 4.12e. Note again that richer input information provided by a larger sensing range is likely to translate into shorter paths.
1Though comparisons between algorithms belonging to the two paradigms are difficult, one comparison seems to apply here. Using the L∞-norm will result, both in Ref. 84 and in the strategy described here, in a less efficient use of control resources and a “less optimal” time of path execution. Since planning with complete information is a one-time computation, this loss in efficiency is likely to be significant, due to a large deviation over the whole path of the robot's moving reference system from the absolute (world) system. In contrast, in the sensor-based approaches the decoupling of controls occurs again and again, at every step of the motion: The reference system is fixed only for the duration of one step, and so the resulting loss in efficiency should be less.
2If needed, other external forces and constraints can be handled within this model, using for example the technique described in Ref. 95.
3A deeper multistep analysis can in principle produce locally shorter paths. It would not add to safety, however, and is not likely to justify the steep rise in computational expenses.
4A deeper, multistep analysis would be hardly justifiable here because of high computational costs, though occasionally it could produce locally shorter paths.
Sensing, Intelligence, Motion, by Vladimir J. Lumelsky
Copyright © 2006 John Wiley & Sons, Inc.