12
Security Schemes for Smart Grid Communications over Public Networks
In this chapter, we focus on security schemes for smart grid communications over public networks that utility companies subscribe to. Public networks in the smart grid are distinguished from private networks by their independence from utilities. Our proposed security schemes can be applied by utilities even without full control of the communications network to add extra protection on top of existing security provided by network service providers.
12.1 Overview of the Proposed Security Schemes
12.1.1 Background and Motivation
With the introduction of cloud computing, some data must be transmitted through public networks (e.g. the Internet) in smart grid communications [181, 189, 190]. Although public cloud service providers have certain security mechanisms within the cloud, data exchange over the Internet still needs extra protection. We propose to apply identity‐based (ID‐based) security schemes [183–185] to secure data transmission over the Internet. With the proposed security schemes, utility companies can have more security control. Moreover, the communication infrastructure in the smart grid can better handle large numbers of participants.
The foundation of an ID‐based security scheme is public‐key cryptography. Instead of generating keys randomly, an ID‐based security scheme utilizes the unique ID of each participant. By doing so, key management might be more convenient, since some of the keys can be computed locally or even ahead of time. Furthermore, privacy and authentication can still be provided to the participants. In the smart grid information and communication networks (ICT) framework, each component has a unique ID that can be applied to ID‐based security schemes. Specifically, the proposed ID‐based security scheme utilizes public key cryptography where the public key is computed mainly based on the ID of each participant together with an expiration indicator ![]() . Public keys can be computed locally by any legitimate user in the domain. As a result, public keys and related domain secrets can be refreshed easily after each session. Key management is simplified by adopting the proposed ID‐based security scheme. With carefully chosen bilinear pairing operation and other system parameters, ID‐based security schemes can perform efficiently in smart grid communication systems.
. Public keys can be computed locally by any legitimate user in the domain. As a result, public keys and related domain secrets can be refreshed easily after each session. Key management is simplified by adopting the proposed ID‐based security scheme. With carefully chosen bilinear pairing operation and other system parameters, ID‐based security schemes can perform efficiently in smart grid communication systems.
Despite its simplicity, the proposed ID‐based based security scheme can provide security services such as confidentiality, data integrity, and non‐repudiation to the smart grid communications network. In this chapter, the proposed ID‐based security scheme is designed to achieve digital signature and encryption simultaneously; thus the proposed scheme is named ID‐based signcryption (IBSC). The IBSC scheme can be reduced to an ID‐based digital signature for those cases that do not require confidentiality. In order to enhance performance, the proposed IBSC is also modified for session key distribution instead of direct message encryption. In addition, the ID‐based schemes are also applied to achieve delegation of signing rights. With this feature, a utility control center may hand over its data control authority to another (or a few other) control center temporarily during routine maintenance, system failure, etc.
In our proposed ID‐based security, we adopt ![]() instead of
instead of ![]() for public key generation, where
for public key generation, where ![]() is the expiration time of the current session. Once a session expires, all participants will update the corresponding secrets and parameters accordingly. When a participant leaves the system domain, secrets bared by this participant need to be revoked. By adopting
is the expiration time of the current session. Once a session expires, all participants will update the corresponding secrets and parameters accordingly. When a participant leaves the system domain, secrets bared by this participant need to be revoked. By adopting ![]() , if the public key generator (PKG) stops issuing secret keys to the participant that left, key revocation can be done automatically at the beginning of the next session. New messages will not be disclosed to old keys.
, if the public key generator (PKG) stops issuing secret keys to the participant that left, key revocation can be done automatically at the beginning of the next session. New messages will not be disclosed to old keys.
12.1.2 Applications of the Proposed Security Schemes in the Smart Grid
The proposed ID‐based security schemes can be applied to a variety of applications in the smart grid communication infrastructure. For communications between a utility's local control centers and a cloud control center, the proposed ID‐based security schemes may function as follows:
- Encipherment and digital signature. The proposed security schemes can be applied directly to provide both confidentiality and non‐repudiation. For instance, preprocessed metering data sent from local control centers to a cloud control center is encrypted and signed to provide confidentiality and non‐repudiation. Information generated by big data analytics is also encrypted and signed before being sent from the cloud to local control centers.
- Session key distribution. If symmetric ciphers are preferred in some applications in the smart grid communication infrastructure, the proposed identity‐based scheme can be applied to achieve secure session key distribution.
- Signing rights delegation from a local control center to another one. If local control center
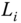 is subject to routine maintenance, it may delegate signing rights to another local control center (e.g.
is subject to routine maintenance, it may delegate signing rights to another local control center (e.g.  ). As shown in Figure 12.1, the private key generator (PKG) controlled by a utility has the authority to delegate signing rights from
). As shown in Figure 12.1, the private key generator (PKG) controlled by a utility has the authority to delegate signing rights from  to
to  . Alternatively,
. Alternatively,  can delegate signing rights to
can delegate signing rights to  locally without involving another entity for more efficient operation.
locally without involving another entity for more efficient operation.

Figure 12.1 Signing rights delegation from 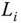 to
to 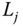 .
. - Signing rights delegation from one local control center to a group of others. The PKG can assign a group of local control centers as a group proxy to sign for
 , as illustrated in Figure 12.2. In this case, no other local control center will take full responsibility for
, as illustrated in Figure 12.2. In this case, no other local control center will take full responsibility for 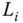 .
.
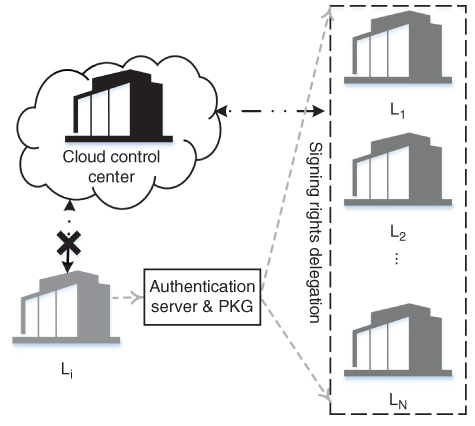
Figure 12.2 Signing rights delegation from  to a group of
to a group of  s.
s.
12.2 Proposed ID‐Based Scheme
The core of the proposed solution is an IBSC scheme, which performs the functions of both digital signature and encryption simultaneously. The scheme can be further applied to achieve digital signature only or key distribution.
12.2.1 Preliminaries
The proposed ID‐based security scheme is based on a bilinear map. Let ![]() and
and ![]() be groups of prime order
be groups of prime order ![]() . Let
. Let ![]() be a generator of
be a generator of ![]() . Let
. Let ![]() . We say that
. We say that ![]() are bilinear map groups if
are bilinear map groups if ![]() has the properties as follows:
has the properties as follows:
- Bilinearity.
 for all
for all  and all
and all  .
. - Nondegeneracy. For any
 ,
, 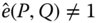 for all
for all 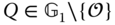 (indicated as
(indicated as  hereafter).
hereafter). - Computability. There is a polynomial time algorithm for computing
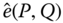 for all
for all 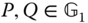 .
.
12.2.2 Identity‐Based Signcryption
The proposed IBSC scheme comprises five algorithms: Setup, Keygen, Signcryption, Decryption, and Verification. Without loss of generality, the algorithms are described using the case where ![]() (
(![]() ) sends message
) sends message ![]() to
to ![]() (
(![]() ).
).
12.2.2.1 Setup
Setup is the algorithm used to initialize a domain's public parameters and set the public/private keys of the authentication server (AS). For simplicity, the AS and PKG are considered interchangeably in the discussion. In practice, they shall be deployed and maintained separately. In Setup, the PKG chooses groups ![]() of prime order
of prime order ![]() , a generator
, a generator ![]() of
of ![]() , a randomly chosen master key
, a randomly chosen master key ![]() , and a domain secret
, and a domain secret ![]() . The PKG also chooses three cryptographic hash functions as follows:
. The PKG also chooses three cryptographic hash functions as follows:

The domain public parameters are
The public/private keys of the AS are ![]() and
and ![]() respectively.
respectively.
12.2.2.2 Keygen
Keygen is the algorithm used to generate public and private keys for each entity in the system. For a given string ![]() and a expiration time stamp
and a expiration time stamp ![]() , the algorithm builds a public/private key pair
, the algorithm builds a public/private key pair ![]() /
/![]() as follows:
as follows:
- Public key:
 .
. - Private key:
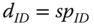 .
.
For example, the keys for ![]() are
are ![]() and
and ![]() . Note that
. Note that ![]() is converted into
is converted into ![]() and is concatenated to
and is concatenated to ![]() in the illustration. Other processes can be taken for the same purpose; for example,
in the illustration. Other processes can be taken for the same purpose; for example, ![]() can also be XORed to
can also be XORed to ![]() .
.
12.2.2.3 Signcryption
Keygen is the algorithm used to encrypt and sign (signcrypt) a message. To signcrypt a message ![]() , sender
, sender ![]()
- randomly picks
 and computes
and computes

- computes
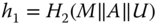 and computes
and computes

- computes
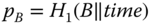 and
and  and then computes
and then computes
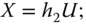
- computes
 and encrypts the message
and encrypts the message

- finally outputs a 4‐tuple
 .
.
In the 4‐tuple, the cipher text is ![]() and the digital signature is
and the digital signature is ![]() .
.
12.2.2.4 Decryption
Decryption is the algorithm used to decrypt a cipher text ![]() . Upon receiving
. Upon receiving ![]() , receiver
, receiver ![]() decrypts
decrypts ![]() in the following steps:
in the following steps:
- computes
 ;
; - decrypts
 .
.
12.2.2.5 Verification
Verification is the algorithm used to validate a digital signature ![]() . Note that the original message
. Note that the original message ![]() must be recovered before verification. A digital signature is verified by
must be recovered before verification. A digital signature is verified by ![]() in the following steps:
in the following steps:
- computes
 , and
, and 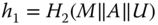 ;
; - verifies if
 .
.
From the illustration we can see that sender ![]() encrypts the message with
encrypts the message with ![]() so that confidentiality is provided. Sender
so that confidentiality is provided. Sender ![]() also signs the message with
also signs the message with ![]() so that non‐repudiation is provided. Data integrity is also provided with hash functions.
so that non‐repudiation is provided. Data integrity is also provided with hash functions.
12.2.3 Consistency of the Proposed IBSC Scheme
We then verify the consistency of the proposed IBSC scheme, in particular, the algorithms Decryption and Verification. The original message ![]() can be recovered with algorithm Decryption if and only if
can be recovered with algorithm Decryption if and only if ![]() . The consistency can be proved as follows:
. The consistency can be proved as follows:
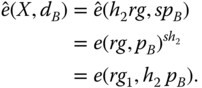
Therefore

The consistency of algorithm Verification is proved as follows:
12.2.4 Identity‐Based Signature
As discussed earlier, not all messages need encryption in smart grid communications. Nonetheless, data integrity and non‐repudiation are still required for most messages. To simplify the computation of each node, the IBSC scheme may be reduced to an identity‐based signature (IBS) scheme for the purpose of digital signature only. The IBS scheme comprises four algorithms, Setup, Keygen, Signature, and Verification. The algorithms Setup and Keygen are the same as the ones in IBSC. The algorithms Signature and Verification are described in the following sections. For consistency, assume ![]() sends
sends ![]() to
to ![]() in the discussion.
in the discussion.
12.2.4.1 Signature
Signature is the algorithm in IBS used to sign a message by sender ![]() . For a given message
. For a given message ![]() , sender
, sender ![]() signs it in the following steps:
signs it in the following steps:
- randomly picks
 and computes
and computes

- computes
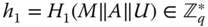 and computes
and computes
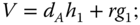
- finally outputs
 .
.
12.2.4.2 Verification
Verification is the algorithm on the receiver side used to validate a digital signature. The receiver ![]() verifies a digital signature
verifies a digital signature ![]() in the following steps:
in the following steps:
- computes
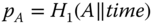 and
and 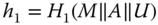 ;
; - verifies if
 .
.
This completes the description of the IBS scheme. The consistency has been is proven by Eq. (12.3).
12.2.5 Key Distribution and Symmetrical Cryptography
Although encryption is achieved in the IBSC scheme, some may still prefer symmetric ciphers for data encryption. Because the proposed identity‐based schemes are based on bilinear pairing (over elliptic curves) with large numbers, they are considerably slower compared to well‐established symmetric ciphers (e.g. advanced encryption standard). Therefore, the IBSC can be modified for session key distribution with symmetric ciphers (e.g. ![]() ) for the actual data encryption. In the modified IBSC, the algorithms Setup and Keygen are unchanged and generate domain public parameters. The algorithm Signcryption is modified to encrypt a message
) for the actual data encryption. In the modified IBSC, the algorithms Setup and Keygen are unchanged and generate domain public parameters. The algorithm Signcryption is modified to encrypt a message ![]() with a secret key
with a secret key ![]() as follows:
as follows:
- Sender
 randomly picks
randomly picks  and sets
and sets
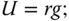
- computes
 and computes
and computes

- computes
 and
and 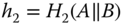 , and computes
, and computes

- computes
 and encrypts the message
and encrypts the message

- encrypts
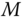 as
as 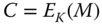 ;
; - finally outputs a 5‐tuple
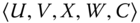 .
.
The algorithm provides a digital signature in the same way that the original IBSC does. The consistency of the modified IBSC follows the original scheme.
12.3 Single Proxy Signing Rights Delegation
In some cases, the signing right of a specific local control center can be delegated to another local control center. A certificate is provided by the local control center itself or the PKG for signing right delegation.
12.3.1 Certificate Distribution by the Local Control Center
Let ![]() be the certificate of signing right delegated by
be the certificate of signing right delegated by ![]() to
to ![]() . A simple example of such a certificate could be
. A simple example of such a certificate could be ![]() , where
, where ![]() is the expiration time of
is the expiration time of ![]() . A certificate can be valid for one message or for all messages before expiration of the certificate. The local control center
. A certificate can be valid for one message or for all messages before expiration of the certificate. The local control center ![]() delegates
delegates ![]() for a message
for a message ![]() in the following steps:
in the following steps:
 randomly picks
randomly picks  and computes
and computes

- computes
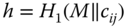 and computes
and computes
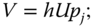
- sets
 .
.
Signing rights delegation is a 4‐tuple ![]() . Once
. Once ![]() receives the
receives the ![]() , it verifies
, it verifies ![]() if
if ![]() . The consistency is shown in the following:
. The consistency is shown in the following:
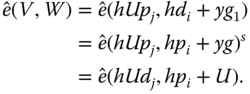
12.3.2 Signing Rights Delegation by the PKG
Alternatively, the PKG is able to distribute a certificate ![]() to
to ![]() in the following steps:
in the following steps:
- The PKG randomly picks
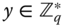 and computes
and computes
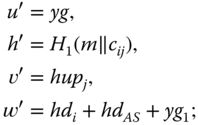
- it finally outputs a 5‐tuple
 .
.
The delegation ![]() is verified by
is verified by ![]() if
if ![]() . The consistency is shown in the following:
. The consistency is shown in the following:
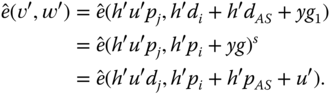
12.3.3 Single Proxy Signature
With certificate ![]() ,
, ![]() is ready to sign message
is ready to sign message ![]() on behalf of
on behalf of ![]() in the following steps:
in the following steps:
 randomly picks
randomly picks  and computes
and computes

- it finally outputs a 5‐tuple
 .
.
The proxy signature is ![]() (note that
(note that ![]() ,
, ![]() , and
, and ![]() are from
are from ![]() ). A receiver verifies
). A receiver verifies ![]() by checking if the equation holds as follows:
by checking if the equation holds as follows:
The consistency is shown in the following,
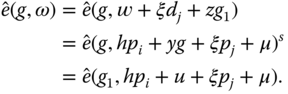
12.4 Group Proxy Signing Rights Delegation
The group proxy signing right of a local control center ![]() is delegated by the PKG to a chosen group of local control centers (e.g.
is delegated by the PKG to a chosen group of local control centers (e.g. ![]() for some
for some ![]() ). Without loss of generality, assume a total number
). Without loss of generality, assume a total number ![]() local control centers are chosen as a group in the discussion.
local control centers are chosen as a group in the discussion.
12.4.1 Certificate Distribution
For each ![]() in the group, the PKG generates a partial signing right certificate
in the group, the PKG generates a partial signing right certificate ![]() and
and
- randomly picks
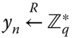 and computes
and computes

- and finally outputs a 5‐tuple
 .
.
Once ![]() receives the
receives the ![]() , it verifies the certificate by checking if
, it verifies the certificate by checking if ![]() .
.
12.4.2 Partial Signature
With ![]() ,
, ![]() can generate a partial signature for message
can generate a partial signature for message ![]() in the following steps:
in the following steps:
 randomly picks
randomly picks 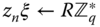 and computes
and computes
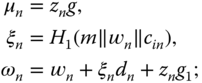
- finally outputs a 5‐tuple
 .
.
12.4.3 Group Signature
After all the proxies have generated partial signatures, one of the local control centers is chosen as the gateway (e.g. ![]() ) and generates a group signature in the following steps:
) and generates a group signature in the following steps:
 computes
computes

- finally outputs
 .
.
A receiver verifies the group signature ![]() by checking if the equation holds as follows:
by checking if the equation holds as follows:

The consistency can be verified such that

12.5 Security Analysis of the Proposed Schemes
12.5.1 Assumptions for Security Analysis
The security of the IBSC and IBS schemes is based on the following computational problems [184, 185, 188]:
- Computational Diffie‐Hellman (CDH) problem. Given
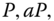 and
and 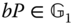 , for all
, for all 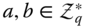 compute
compute  in polynomial time.
in polynomial time. - Bilinear Diffie‐Hellman (BDH) problem. Given
 and
and 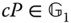 , for all
, for all 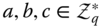 compute
compute  in polynomial time.
in polynomial time.
Without loss of generality, time stamp ![]() is considered part of the identity
is considered part of the identity ![]() in the analysis later. To make the illustration clearer, the proposed IBSC scheme is separated into an identity‐based encryption scheme and identity‐based signature for security analysis. Moreover, all random values are picked uniformly unless otherwise specified.
in the analysis later. To make the illustration clearer, the proposed IBSC scheme is separated into an identity‐based encryption scheme and identity‐based signature for security analysis. Moreover, all random values are picked uniformly unless otherwise specified.
12.5.2 Identity‐Based Encryption Security
12.5.2.1 Security Model
Definition 1 Semantic security for identity‐based encryption (IBE) schemes [188]. If no probabilistic polynomial time adversary has a nonnegligible advantage in this game:
- The challenger runs the setup algorithm to generate the system's parameters and sends them to the adversary.
- The adversary
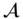 performs a series of queries:
performs a series of queries:
- Key extraction queries.
 produces an identity ID and receives the private key
produces an identity ID and receives the private key 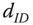 .
. - Challenge. After a polynomial number of queries,
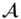 outputs two equal‐length plaintexts
outputs two equal‐length plaintexts  and
and 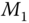 and a public key ID on which it wishes to be challenged (ID has not appeared in private key queries). The challenger picks a random bit
and a public key ID on which it wishes to be challenged (ID has not appeared in private key queries). The challenger picks a random bit  and encrypts
and encrypts 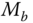 according to the IBE scheme.
according to the IBE scheme. - More key extraction queries.
 issues more key extraction queries. The challenger responds as before.
issues more key extraction queries. The challenger responds as before.
- Key extraction queries.
Finally, the adversary ![]() outputs a guess
outputs a guess ![]() ,
, ![]() wins the game if
wins the game if ![]() .
.
12.5.2.2 Security Analysis
12.5.3 Identity‐Based Signature Security
12.5.3.1 Security Models
Definition 2 Strongly existentially unforgeable identity‐based signature scheme under chosen‐message attacks [184]. If no probabilistic polynomial time adversary has a nonnegligible advantage in this game:
- The challenger runs the setup algorithm to generate the system's parameters and sends them to the adversary.
- The adversary
 performs a series of queries:
performs a series of queries:
- Key extraction queries.
 produces an identity
produces an identity 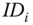 and receives the private key
and receives the private key 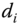 .
. - Signature queries
 produces a message
produces a message  and an identity
and an identity 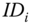 and receives a signature on
and receives a signature on  that was generated by the signature oracle using the private key corresponding to the identity
that was generated by the signature oracle using the private key corresponding to the identity  (i.e.
(i.e.  ).
). - After a polynomial number of queries,
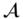 produces a tuple
produces a tuple  made of an identity
made of an identity 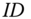 , whose corresponding private key was never asked during stage 2, and a message signature pair
, whose corresponding private key was never asked during stage 2, and a message signature pair 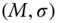 such that
such that  was not returned by the signature oracle on the input
was not returned by the signature oracle on the input  during stage 2 for the identity
during stage 2 for the identity  .
.
- Key extraction queries.
![]() wins the game if the forged signature can be verified when the verification algorithms run on the tuple
wins the game if the forged signature can be verified when the verification algorithms run on the tuple ![]() . The forger's advantage is defined to be its probability of producing a forgery taken over the number of coin‐flipping of the challenger and
. The forger's advantage is defined to be its probability of producing a forgery taken over the number of coin‐flipping of the challenger and ![]() .
.
12.5.3.2 Security Analysis
12.6 Performance Analysis of the Proposed Schemes
In this section, we evaluate the performance of the proposed schemes.
12.6.1 Computational Complexity of the Proposed Schemes
Performance of the proposed schemes is based on the number of operations and the efficiency of each type of operations. Table 12.1 lists the number of operations of each algorithm in the proposed security scheme. Among them, ![]() indicates standard multiplication in
indicates standard multiplication in ![]() . Since addition in
. Since addition in ![]() and XOR are simple and efficient operations, they are not listed in the table.
and XOR are simple and efficient operations, they are not listed in the table.
Table 12.1 Computational complexity.
| # of | # of | # of | # of | # of | |
| Signcrypt | 1 | 5 | 1 | 2 | 1 |
| Decrypt | 1 | 0 | 0 | 0 | 1 |
| Sign | 0 | 3 | 1 | 0 | 0 |
| Verify | 3 | 1 | 1 | 1 | 0 |
Hash functions can be computed efficiently in general. In practice, ![]() and
and ![]() are easy to find. However, it is hard to build
are easy to find. However, it is hard to build ![]() . In the analysis, we relax
. In the analysis, we relax ![]() into two steps as follows:
into two steps as follows:
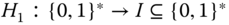 ;
;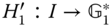 .
.
In step 1, ![]() is a finite set, and
is a finite set, and ![]() is an encoding function which is computable. Note that after the relaxation, the public key for a given
is an encoding function which is computable. Note that after the relaxation, the public key for a given ![]() and
and ![]() is calculated as
is calculated as ![]() . In the proposed IBSC scheme, public keys can be computed at the beginning of each session and cached for the entire session. Therefore, the relaxation of
. In the proposed IBSC scheme, public keys can be computed at the beginning of each session and cached for the entire session. Therefore, the relaxation of ![]() does not introduce more computational cost in reality. Because of that, performance of the IBSC and IBS schemes will be considered efficient if bilinear pairing
does not introduce more computational cost in reality. Because of that, performance of the IBSC and IBS schemes will be considered efficient if bilinear pairing ![]() and multiplication in
and multiplication in ![]() can be computed efficiently. Since the Weil pairing can be performed efficiently using Miller's algorithm [191], the bilinear map
can be computed efficiently. Since the Weil pairing can be performed efficiently using Miller's algorithm [191], the bilinear map ![]() can be performed efficiently as well.
can be performed efficiently as well.
12.6.2 Choosing Bilinear Paring Functions
To analyze the performance of the IBSC scheme, we apply two bilinear pairing functions, modified Weil pairing and Tate pairing, over supersingular elliptic curve ![]() .
.
We first construct ![]() . Let
. Let ![]() be a prime number such that
be a prime number such that ![]() and
and ![]() for some prime
for some prime ![]() and positive integer
and positive integer ![]() . Then
. Then ![]() is the subgroup of order
is the subgroup of order ![]() of
of ![]() . The CDH problem is hard in the group
. The CDH problem is hard in the group ![]() [188, 192]. However, it is worth mentioning that the decisional Diffie‐Hellman (DDH) problem is an easy one for bilinear map
[188, 192]. However, it is worth mentioning that the decisional Diffie‐Hellman (DDH) problem is an easy one for bilinear map ![]() . This is because with given
. This is because with given ![]() ,
, ![]() , we can easily check if
, we can easily check if ![]() by comparing
by comparing ![]() with
with ![]() .
.
The Weil pairing ![]() has the properties of bilinearity and computability; however, it does not have nondegeneracy. Therefore, we adopt a modified Weil pairing
has the properties of bilinearity and computability; however, it does not have nondegeneracy. Therefore, we adopt a modified Weil pairing ![]() such that
such that ![]() , where
, where ![]() is an automorphism on the group of points of supersingular elliptic curve
is an automorphism on the group of points of supersingular elliptic curve ![]() , that is,
, that is, ![]() , where
, where ![]() is a primitive cube root of unity in
is a primitive cube root of unity in ![]() . Thus,
. Thus, 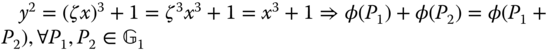 . The bilinear map
. The bilinear map ![]() is calculated as a Weil pairing with an additional standard multiplication on the curve
is calculated as a Weil pairing with an additional standard multiplication on the curve ![]() . According to [188],
. According to [188], ![]() is believed to satisfy the BDH problem. However, computing the discrete logarithm in
is believed to satisfy the BDH problem. However, computing the discrete logarithm in ![]() is sufficient for computing the discrete logarithm in
is sufficient for computing the discrete logarithm in ![]() . Therefore, in order to make it sufficiently hard in practice,
. Therefore, in order to make it sufficiently hard in practice, ![]() needs to be at least 512 bits long.
needs to be at least 512 bits long.
12.6.3 Numerical Results
We evaluate the proposed identity‐based schemes with modified Weil pairing ![]() using Mathematica 10.0 on a computer equipped with an Intel Core i5‐2400
using Mathematica 10.0 on a computer equipped with an Intel Core i5‐2400 ![]() GHz and 12 GB RAM. We first show the computational cost of each operation. Since
GHz and 12 GB RAM. We first show the computational cost of each operation. Since ![]() ,
, ![]() , and
, and ![]() do not have much difference in computational time and the added encoding function
do not have much difference in computational time and the added encoding function ![]() is more efficient than
is more efficient than ![]() , the hash functions are excluded from the performance analysis.
, the hash functions are excluded from the performance analysis.
Table 12.2 Computational time for each operation.
| Bilinear pairing | Standard multiplication | ||
| 7.44 ms | 13.25 ms | 6.43 ms | 12.29 ms |
First, we evaluate the computational time for the bilinear pairing ![]() . Two sets of evaluation are given, that is, for
. Two sets of evaluation are given, that is, for ![]() bits and
bits and ![]() bits. Each evaluation is the average value from
bits. Each evaluation is the average value from ![]() calculations. With
calculations. With ![]() bits, one
bits, one ![]() takes about 7.44 ms. With
takes about 7.44 ms. With ![]() bits, one
bits, one ![]() takes about 13.25 ms. We then evaluate the computational time of standard multiplication over
takes about 13.25 ms. We then evaluate the computational time of standard multiplication over ![]() (i.e.
(i.e. ![]() ). The computational time of
). The computational time of ![]() mainly depends on the size of
mainly depends on the size of ![]() (assuming
(assuming ![]() bits). The computational time of each evaluation is averaged from
bits). The computational time of each evaluation is averaged from ![]() calculations. With
calculations. With ![]() bits, a standard multiplication operation takes about
bits, a standard multiplication operation takes about ![]() ms. Note that in the proposed IBSC,
ms. Note that in the proposed IBSC, ![]() is the output of some hash functions; therefore,
is the output of some hash functions; therefore, ![]() usually is 256 bits or 512 bits, where the computation is efficient. The evaluation results are summarized in Table 12.2.
usually is 256 bits or 512 bits, where the computation is efficient. The evaluation results are summarized in Table 12.2.
Table 12.3 Computational time of each algorithm.
| Signcrypt | 39.59 ms | 68.89 ms | 45.4 ms | 74.7 ms |
| Decrypt | 7.44 ms | 7.44 ms | 13.25 ms | 13.25 ms |
| Sign | 19.29 ms | 36.87 ms | 19.29 ms | 36.87 ms |
| Verify | 28.75 ms | 34.61 ms | 46.18 ms | 52.04 ms |
Based on the evaluations we have for each operation, we then show the total operational time for each algorithm. In practice, public keys are computed once and cached for the entire session. The computational time of each algorithm is listed in Table 12.3 ( where “b” stands for “bits”). It is shown that the proposed IBSC performs efficiently for delay‐tolerant and even near real‐time data transmission, for example, metering data transmission. However, for real‐time monitoring data, such as PMU data, the identity‐based schemes alone may not be a good solution. Without sufficient computational resources, faster security protocols and schemes are recommended, for instance, traditional symmetric ciphers. The proposed IBSC can be applied for initial authentication and key distribution of the chosen symmetric ciphers.
12.7 Conclusion
In this chapter, we proposed an ID‐based signcryption security scheme for smart grid communications over public networks. The proposed IBSC scheme performs simultaneously the functions of encryption and digital signature. Therefore, confidentiality, non‐repudiation, and data integrity are provided in a single calculation. The proposed IBSC scheme was also reduced to a ID‐based digital signature scheme if confidentiality is not required for some messages. To further enhance the performance, symmetric ciphers were introduced to the IBSC. In addition, delegation of signing rights from one local control center to another (or a few) local control center was achieved by the proposed identity‐based schemes. The security of the proposed IBSC was studied. The numerical results showed that the proposed IBSC scheme is able to perform efficiently with security guarantee in the cyber‐physical system of the smart grid.

