123
en,
L
V
F
= mω
V
r
2
+
mr
2
ω
V
=
3
mω
V
r
2
.
2 2
Because L
V
F
= L
IV
F
, then:
3
mω
V
r
2
= mω
IV
r
2
cos α +
1
,
2 2
and from here
ω
V
=
ω
IV
(2 cos α + 1))
. (6.4)
3
Using Carnot’s theorem we will verify the obtained expression for the angular velocity of the cylinder (for the case
when an ideally inelastic support is applied to the system of particles):
T
IV
– T
V
= T
*
.
e kinetic energy of the cylinder prior of its impact with the inclined plane:
T
IV
=
1
mv
C
IV
+
1
C
ω
IV
=
1
mω
IV
r
2
+
1
∙
mr
2
ω
IV
=
1
∙
3mr
2
ω
IV
=
1
F
ω
IV
.
2
2
2
2
2
2
2
2
e kinetic energy of the cylinder after the impact with the inclined plane:
T
V
=
1
mv
C
V
+
1
C
ω
V
2
=
1
mω
V
2
r2 +
1
∙
mr
2
ω
V
2
=
1
∙
3mr
2
ω
V
2
=
1
F
ω
V
2
.
2
2
2
2
2
2
2
2
C
E
v
CIV
ω
IV
V
K
F
ε
ω
V
s
F
s
F
v
CIV
IV
90°
90°
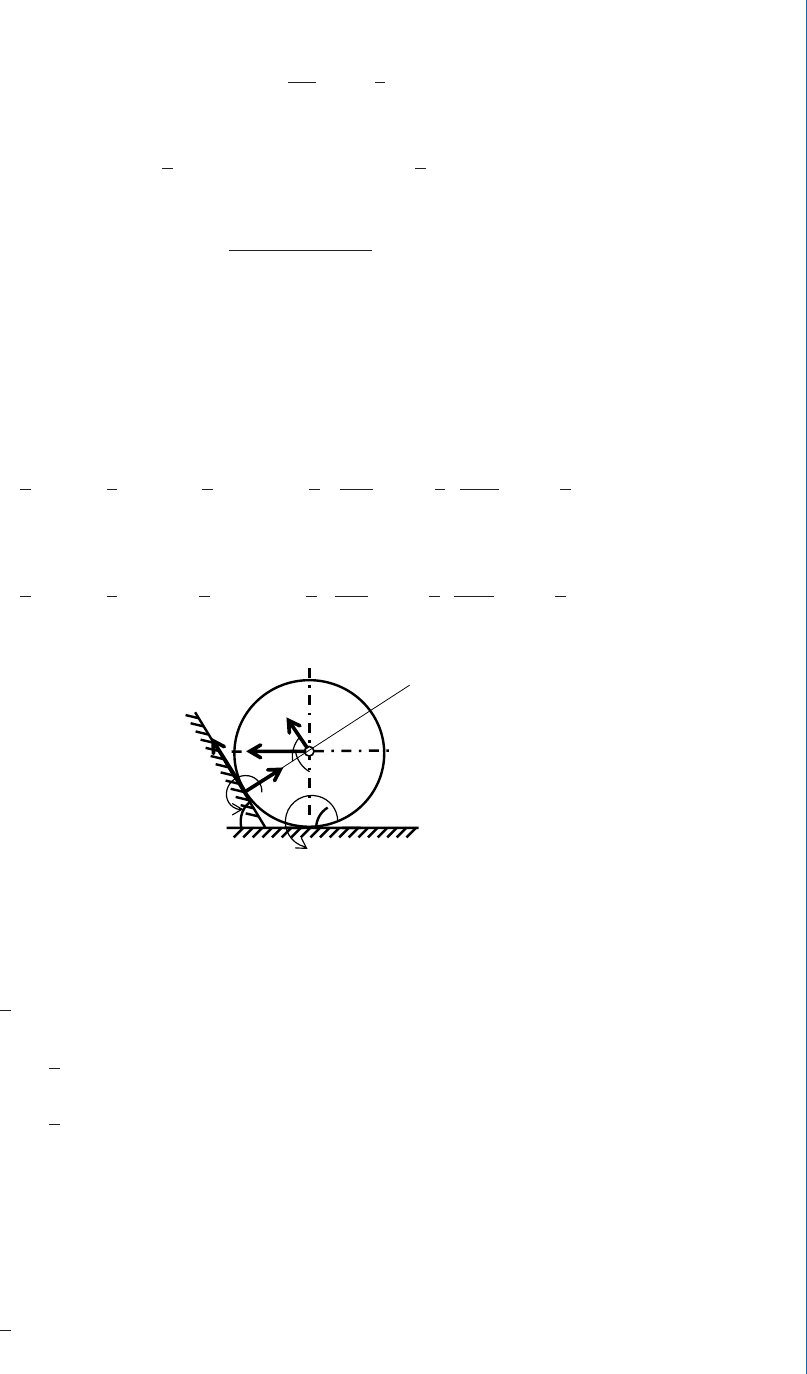
Figure 6.36.
e kinetic energy of the cylinder corresponding to its lost velocities ∆v
⃗
i
IV
= v
⃗
i
IV
– v
⃗
i
V
(Figure 6.37):
T
*
=
1
m
i
(v
⃗
i
IV
– v
⃗
i
V
)
2
2
=
1
m
i
v
⃗
i
IV
v
⃗
i
IV
– 2v
⃗
i
IV
v
⃗
i
V
+ v
⃗
i
V
v
⃗
i
V
2
=
1
m
i
v
i
IV
– 2v
i
V
cos φi + v
i
V
.
2
Here:
v
i
IV
= ω
IV
EMi – is the velocity of the particle M
i
before the impact;
v
i
V
= ω
V
EMi – is the velocity of the particle M
i
after the impact.
en,
T
*
=
1
m
i
ω
i
IV
(EM
i
)
2
2
2
2 2
2
2 2 2 2 2
6.3 SOLUTION

124 6. TOPIC AK-6
–
1
2m
i
ω
IV
EM
i
ω
V
FM
i
cos φ
i
2
+
1
2m
i
ω
V
2
(FM
i
)
2
2
=
1
ω
IV
m
i
(EM
i
)
2
2
–
1
ω
IV
ω
V
2m
i
EM
i
FM
i
cos φ
i
+
1
ω
V
2
m
i
(FM
i
)
2
.
2
From the triangle ∆M
i
EF:
(EF)
2
= (FM
i
)
2
+ (EM
i
)
2
– 2FM
i
EM
i
cos φ
i
.
erefore,
–2m
i
EM
i
FM
i
cos φ
i
= m
i
[(EF)
2
– (FM
i
)
2
– (EM
i
)
2
]
= m
i
(EF)
2
– m
i
(FM
i
)
2
– m
i
(EM
i
)
2
= (EF)
2
m
i
–
F
– E.
en,
T* =
1
ω
IV
m
i
(EM
i
)
2
+
1
ω
IV
ω
I
[m(EF)
2
–
F
–
E
]
2
2
+
1
ω
V
2
m
i
(FM
i
)
2
2
=
1
E
ω
IV
+
1
mω
IV
ω
V
(EF)
2
–
1
F
ω
IV
ω
V
–
1
E
ω
IV
ω
V
+
1
F
ω
V
2
.
2
2
2
2
2
However,
F
=
E
=
F(E)
.
From triangle ∆CEF:
EF = 2r sin
α
.
2
erefore,
T* =
1
E
ω
IV
+
1
mω
IV
ω
V
4r
2
sin
2
α
–
F(E)
mω
IV
ω
V
+
1
F
ω
V
2
.
2
2
2
2
Hence,
1
E
ω
IV
–
1
F
ω
V
2
=
1
E
ω
IV
+ 2mω
IV
ω
V
4r
2
sin
2
α
–
F(E)
ω
IV
ω
V
+
1
F
ω
V
2
,
2
2
2
2
2
or
–
F
ω
V
2
= 2mω
IV
ω
V
r
2
sin
2
α
–
F(E)
ω
IV
ω
V
,
2
e.g.,
–
3
mr
2
ω
V
2
= 2mω
IV
ω
V
r
2
sin
2
α
–
3
mr
2
ω
IV
ω
V
.
2
2
2
From here:
2
2
2
2
2 2

125
ω
V
=
ω
IV
-4sin
2
α
+ 3
=
ω
IV
[–2(1 – cos α) + 3]
3
3
or
ω
V
=
ω
IV
2cos
α
+ 1
.
3
C
E
ω
IV
V
K
F
ω
V
IV
90°
90°
Δv
i
v
iIV
v
iV
γ
i
Figure 6.37.
Next, we apply the kinetic energy work principle for the mechanical system, which corresponds to the rolling of the
cylinder along the inclined plane from the position V to the position VI at the distance s (Figure 6.38):
T
VI
– T
V
=A
i
E
.
Because T
VI
= 0,
–
mv
CV
+
J
C
ω
V
2
= Gs sin α
2 2
or
–
mω
V
2
r
2
–
mr
2
ω
V
2
= – mgs sin α,
2 2
e.g.,
3
ω
V
2
r
2
= gs sin α.
4
From here:
ω
V
=
2
gs sin α
. (6.5)
4 3
From Equations (6.2)–(6.4) we can nd:
ω
II
=
9ω
V
2
+
4gh
.
(2 cos α + 1)
2
3r
2
Considering Equation (6.5):
ω
II
=
2
3gs
sin α
+
gh
.
4
(2 cos α + 1)
2
3
us, according to Equation (6.1), the velocity of the platform:
v =
3r
2
∙
2
3gs
sin α
+
gh
2(r – h) r
(2 cos α + 1)
2
2
2
2
6.3 SOLUTION
2

126 6. TOPIC AK-6
=
3 ∙ 0.5
3 ∙ 9.81 ∙ 0.1 ∙ 0.866
+
4 ∙ 9.81 ∙ 0.1
= 3.68
m
.
0.5 – 0.1 (2 ∙ 0.5 + 1)
2
3 s
C
G
VI
K
F
s
ω
V
v
CV
V
N
C
Figure 6.38.
To nd the impact impulse on the cylinder from the step, we will apply the linear momentum impulse principle for
the mechanical system during the impact in algebraic form on x and y axes (Figure 6.32):
mv
C
II
x
– mv
C
I
x
= S
i
x
,
mv
C
II
y
– mv
C
I
y
= S
i
x
,
or
–mv
C
II
cos β – (–mv
C
I
) = S
D
x
,
mv
C
II
sin β = S
D
y
.
From here:
S
D
x
= mv
C
I
– mv
C
II
cos β = mv – mω
II
r
r – h
= mv 1 –
2(r – h)
2
= 500 ∙ 3.68 1 –
2(0.5 – 0.1)
2
= 1,055 N ∙ s,
r
3r
2
3· 0.5
2
S
D
y
= mv
C
II
sin β = mωII r√1 – cos
2
β =
2(r – h)mv
1 –
(r – h)
2
=
2(0.5 – 0.1)500 ∙ 3.68
∙ 0.6 = 589 N ∙ s.
3r
r
2
3∙0.5
Then, the impact impulse on the cylinder from the step:
S
D
= S
D
x
+ S
D
y
= √1,055
2
+ 589
2
= 1,208 N ∙ s.
To nd the impact impulse on the cylinder from the inclined plane, we will apply the linear momentum impulse
principle for the mechanical system during the impact in algebraic form on ξ and η axes (Figure 6.36):
mv
C
V
ξ
– mv
C
IV
ξ
= S
i
ξ
,
mv
C
V
η
– mv
C
IV
η
= S
i
η
,
or
–(–mv
C
IV
) sin α = S
F
ξ
,
E
E
2 2
E
E

127
mv
C
V
– mv
C
IV
cos α = S
F
η
.
From here:
S
F
ξ
= mv
C
IV
sin α = mω
IV
r sin α = m
3ω
V
r sin α,
2 cos α + 1
S
F
η
= mv
C
V
– mv
C
IV
cos α = mω
V
r – mω
IV
r cos α = mω
V
r – m
3ω
V
r cos α.
2 cos α + 1
Using the equation (6.5) we will nd:
S
F
ξ
=
6m
gs sin α
sin α =
6 ∙ 500
9.81 ∙ 0.1 ∙ 0.866
∙ 0.866 = 691 N ∙ s,
2 cos α +1
2 · 0.5 +1
S
F
η
= 2m
gs sin α
1 –
3 cos α
= 2 ∙ 500
9.81 ∙ 0.1 ∙ 0.866
1 –
3 ∙ 0.5
=133 N ∙ s.
3 2 cos α + 1 3 2 · 0.5 + 1
e impact impulse on the cylinder from the inclined plane:
S
F
= S
F
ξ
+ S
F
η
= √691
2
+ 133
2
= 704 N ∙ s.
3 3
6.3 SOLUTION
2 2
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
