1
Fundamentals
The hardest part of any statistical work is getting started. And one of the hardest things about getting started is choosing the right kind of statistical analysis. The choice depends on the nature of your data and on the particular question you are trying to answer. The truth is that there is no substitute for experience: the way to know what to do is to have done it properly lots of times before.
The key is to understand what kind of response variable you have got, and to know the nature of your explanatory variables. The response variable is the thing you are working on: it is the variable whose variation you are attempting to understand. This is the variable that goes on the y axis of the graph (the ordinate). The explanatory variable goes on the x axis of the graph (the abscissa); you are interested in the extent to which variation in the response variable is associated with variation in the explanatory variable. A continuous measurement is a variable like height or weight that can take any real numbered value. A categorical variable is a factor with two or more levels: sex is a factor with two levels (male and female), and rainbow might be a factor with seven levels (red, orange, yellow, green, blue, indigo, violet).
It is essential, therefore, that you know:
- which of your variables is the response variable?
- which are the explanatory variables?
- are the explanatory variables continuous or categorical, or a mixture of both?
- what kind of response variable have you got – is it a continuous measurement, a count, a proportion, a time-at-death, or a category?
These simple keys will then lead you to the appropriate statistical method:
- The explanatory variables (pick one of the rows):
(a) All explanatory variables continuous Regression (b) All explanatory variables categorical Analysis of variance (ANOVA) (c) Some explanatory variables continuous some categorical Analysis of covariance (ANCOVA) - The response variable (pick one of the rows):
(a) Continuous Regression, ANOVA or ANCOVA (b) Proportion Logistic regression (c) Count Log linear models (d) Binary Binary logistic analysis (e) Time at death Survival analysis
There is a small core of key ideas that need to be understood from the outset. We cover these here before getting into any detail about different kinds of statistical model.
Everything Varies
If you measure the same thing twice you will get two different answers. If you measure the same thing on different occasions you will get different answers because the thing will have aged. If you measure different individuals, they will differ for both genetic and environmental reasons (nature and nurture). Heterogeneity is universal: spatial heterogeneity means that places always differ, and temporal heterogeneity means that times always differ.
Because everything varies, finding that things vary is simply not interesting. We need a way of discriminating between variation that is scientifically interesting, and variation that just reflects background heterogeneity. That is why you need statistics. It is what this whole book is about.
The key concept is the amount of variation that we would expect to occur by chance alone, when nothing scientifically interesting was going on. If we measure bigger differences than we would expect by chance, we say that the result is statistically significant. If we measure no more variation than we might reasonably expect to occur by chance alone, then we say that our result is not statistically significant. It is important to understand that this is not to say that the result is not important. Non-significant differences in human life span between two drug treatments may be massively important (especially if you are the patient involved). Non-significant is not the same as ‘not different’. The lack of significance may be due simply to the fact that our replication is too low.
On the other hand, when nothing really is going on, then we want to know this. It makes life much simpler if we can be reasonably sure that there is no relationship between y and x. Some students think that ‘the only good result is a significant result’. They feel that their study has somehow failed if it shows that ‘A has no significant effect on B’. This is an understandable failing of human nature, but it is not good science. The point is that we want to know the truth, one way or the other. We should try not to care too much about the way things turn out. This is not an amoral stance, it just happens to be the way that science works best. Of course, it is hopelessly idealistic to pretend that this is the way that scientists really behave. Scientists often want passionately that a particular experimental result will turn out to be statistically significant, so that they can get a Nature paper and get promoted. But that does not make it right.
Significance
What do we mean when we say that a result is significant? The normal dictionary definitions of significant are ‘having or conveying a meaning’ or ‘expressive; suggesting or implying deeper or unstated meaning’. But in statistics we mean something very specific indeed. We mean that ‘a result was unlikely to have occurred by chance’. In particular, we mean ‘unlikely to have occurred by chance if the null hypothesis was true’. So there are two elements to it: we need to be clear about what we mean by ‘unlikely’, and also what exactly we mean by the ‘null hypothesis’. Statisticians have an agreed convention about what constitutes ‘unlikely’. They say that an event is unlikely if it occurs less than 5% of the time. In general, the null hypothesis says that ‘nothing is happening’ and the alternative says that ‘something is happening’.
Good and Bad Hypotheses
Karl Popper was the first to point out that a good hypothesis was one that was capable of rejection. He argued that a good hypothesis is a falsifiable hypothesis. Consider the following two assertions:
- there are vultures in the local park
- there are no vultures in the local park
Both involve the same essential idea, but one is refutable and the other is not. Ask yourself how you would refute option A. You go out into the park and you look for vultures. But you do not see any. Of course, this does not mean that there are none. They could have seen you coming, and hidden behind you. No matter how long or how hard you look, you cannot refute the hypothesis. All you can say is ‘I went out and I didn't see any vultures’. One of the most important scientific notions is that absence of evidence is not evidence of absence.
Option B is fundamentally different. You reject hypothesis B the first time you see a vulture in the park. Until the time that you do see your first vulture in the park, you work on the assumption that the hypothesis is true. But if you see a vulture, the hypothesis is clearly false, so you reject it.
Null Hypotheses
The null hypothesis says ‘nothing is happening’. For instance, when we are comparing two sample means, the null hypothesis is that the means of the two populations are the same. Of course, the two sample means are not identical, because everything varies. Again, when working with a graph of y against x in a regression study, the null hypothesis is that the slope of the relationship is zero (i.e. y is not a function of x, or y is independent of x). The essential point is that the null hypothesis is falsifiable. We reject the null hypothesis when our data show that the null hypothesis is sufficiently unlikely.
p Values
Here we encounter a much-misunderstood topic. The p value is not the probability that the null hypothesis is true, although you will often hear people saying this. In fact, p values are calculated on the assumption that the null hypothesis is true. It is correct to say that p values have to do with the plausibility of the null hypothesis, but in a rather subtle way.
As you will see later, we typically base our hypothesis testing on what are known as test statistics: you may have heard of some of these already (Student's t, Fisher's F and Pearson's chi-squared, for instance): p values are about the size of the test statistic. In particular, a p value is an estimate of the probability that a value of the test statistic, or a value more extreme than this, could have occurred by chance when the null hypothesis is true. Big values of the test statistic indicate that the null hypothesis is unlikely to be true. For sufficiently large values of the test statistic, we reject the null hypothesis and accept the alternative hypothesis.
Note also that saying ‘we do not reject the null hypothesis’ and ‘the null hypothesis is true’ are two quite different things. For instance, we may have failed to reject a false null hypothesis because our sample size was too low, or because our measurement error was too large. Thus, p values are interesting, but they do not tell the whole story: effect sizes and sample sizes are equally important in drawing conclusions. The modern practice is to state the p value rather than just to say ‘we reject the null hypothesis’. That way, the reader can form their own judgement about the effect size and its associated uncertainty.
Interpretation
It should be clear by this point that we can make two kinds of mistakes in the interpretation of our statistical models:
- we can reject the null hypothesis when it is true
- we can accept the null hypothesis when it is false
These are referred to as Type I and Type II errors, respectively. Supposing we knew the true state of affairs (which, of course, we seldom do). Then in tabular form:
| Null hypothesis | Actual situation | |
| True | False | |
| Accept | Correct decision | Type II |
| Reject | Type I | Correct decision |
Model Choice
There are a great many models that we could fit to our data, and selecting which model to use involves considerable skill and experience. All models are wrong, but some models are better than others. Model choice is one of the most frequently ignored of the big issues involved in learning statistics.
In the past, elementary statistics was taught as a series of recipes that you followed without the need for any thought. This caused two big problems. People who were taught this way never realized that model choice is a really big deal (‘I'm only trying to do a t test’). And they never understood that assumptions need to be checked (‘all I need is the p value’).
Throughout this book you are encouraged to learn the key assumptions. In order of importance, these are
- random sampling
- constant variance
- normal errors
- independent errors
- additive effects
Crucially, because these assumptions are often not met with the kinds of data that we encounter in practice, we need to know what to do about it. There are some things that it is much more difficult to do anything about (e.g. non-random sampling) than others (e.g. non-additive effects).
The book also encourages users to understand that in most cases there are literally hundreds of possible models, and that choosing the best model is an essential part of the process of statistical analysis. Which explanatory variables to include in your model, what transformation to apply to each variable, whether to include interaction terms: all of these are key issues that you need to resolve.
The issues are at their simplest with designed manipulative experiments in which there was thorough randomization and good levels of replication. The issues are most difficult with observational studies where there are large numbers of (possibly correlated) explanatory variables, little or no randomization and small numbers of data points. Much of your data is likely to come from the second category.
Statistical Modelling
The object is to determine the values of the parameters in a specific model that lead to the best fit of the model to the data. The data are sacrosanct, and they tell us what actually happened under a given set of circumstances. It is a common mistake to say ‘the data were fitted to the model’ as if the data were something flexible, and we had a clear picture of the structure of the model. On the contrary, what we are looking for is the minimal adequate model to describe the data. The model is fitted to data, not the other way around. The best model is the model that produces the least unexplained variation (the minimal residual deviance), subject to the constraint that the parameters in the model should all be statistically significant.
You have to specify the model. It embodies your mechanistic understanding of the factors involved, and of the way that they are related to the response variable. We want the model to be minimal because of the principle of parsimony, and adequate because there is no point in retaining an inadequate model that does not describe a significant fraction of the variation in the data. It is very important to understand that there is not one model; this is one of the common implicit errors involved in traditional regression and ANOVA, where the same models are used, often uncritically, over and over again. In most circumstances, there will be a large number of different, more or less plausible models that might be fitted to any given set of data. Part of the job of data analysis is to determine which, if any, of the possible models are adequate, and then, out of the set of adequate models, which is the minimal adequate model. In some cases there may be no single best model and a set of different models may all describe the data equally well (or equally poorly if the variability is great).
Maximum Likelihood
What, exactly, do we mean when we say that the parameter values should afford the ‘best fit of the model to the data’? The convention we adopt is that our techniques should lead to unbiased, variance minimizing estimators. We define ‘best’ in terms of maximum likelihood. This notion is likely to be unfamiliar, so it is worth investing some time to get a feel for it. This is how it works:
- given the data
- and given our choice of model
- what values of the parameters of that model
- make the observed data most likely?
Let us take a simple example from linear regression where the model we want to fit is y = a + bx and we want the best possible estimates of the two parameters (the intercept a and the slope b) from the data in our scatterplot.
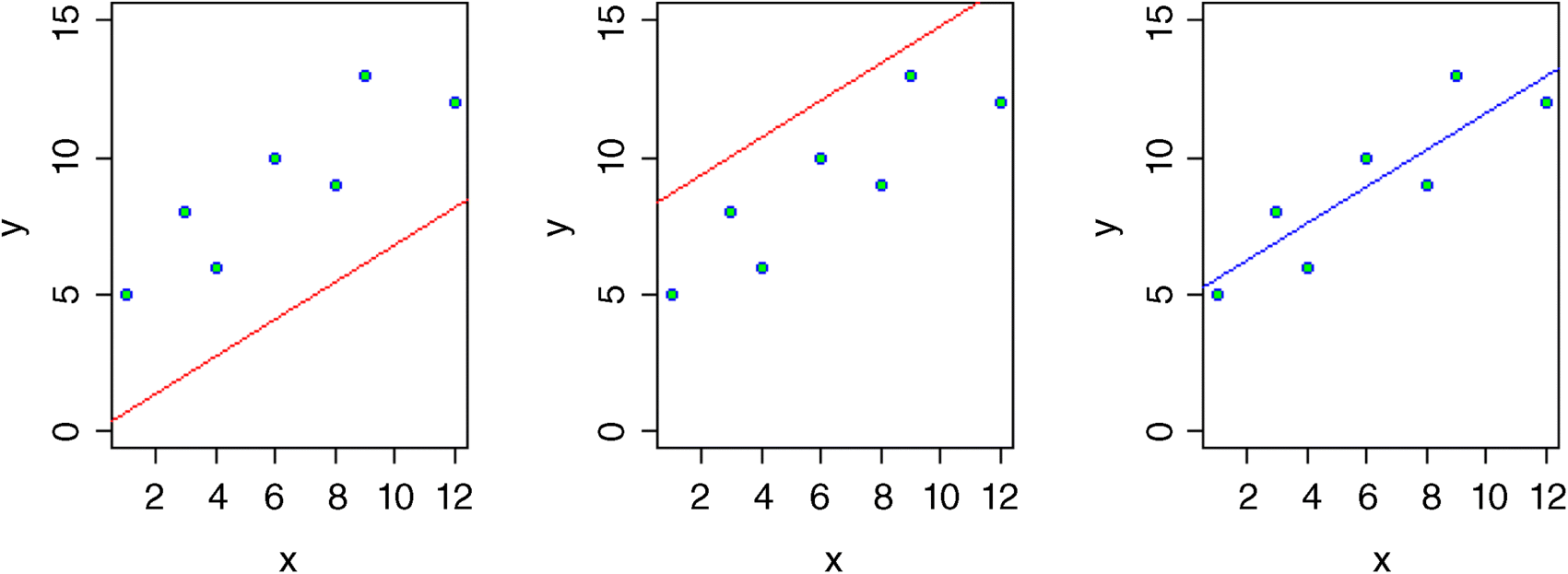
If the intercept were 0 (left-hand graph, above), would the data be likely? The answer of course, is no. If the intercept were 8 (centre graph) would the data be likely? Again, the answer is obviously no. The maximum likelihood estimate of the intercept is shown in the right-hand graph (its value turns out to be 4.827). Note that the point at which the graph cuts the y axis is not the intercept when (as here) you let R decide where to put the axes.
We could have a similar debate about the slope. Suppose we knew that the intercept was 4.827, then would the data be likely if the graph had a slope of 1.5 (left-hand graph, below)?
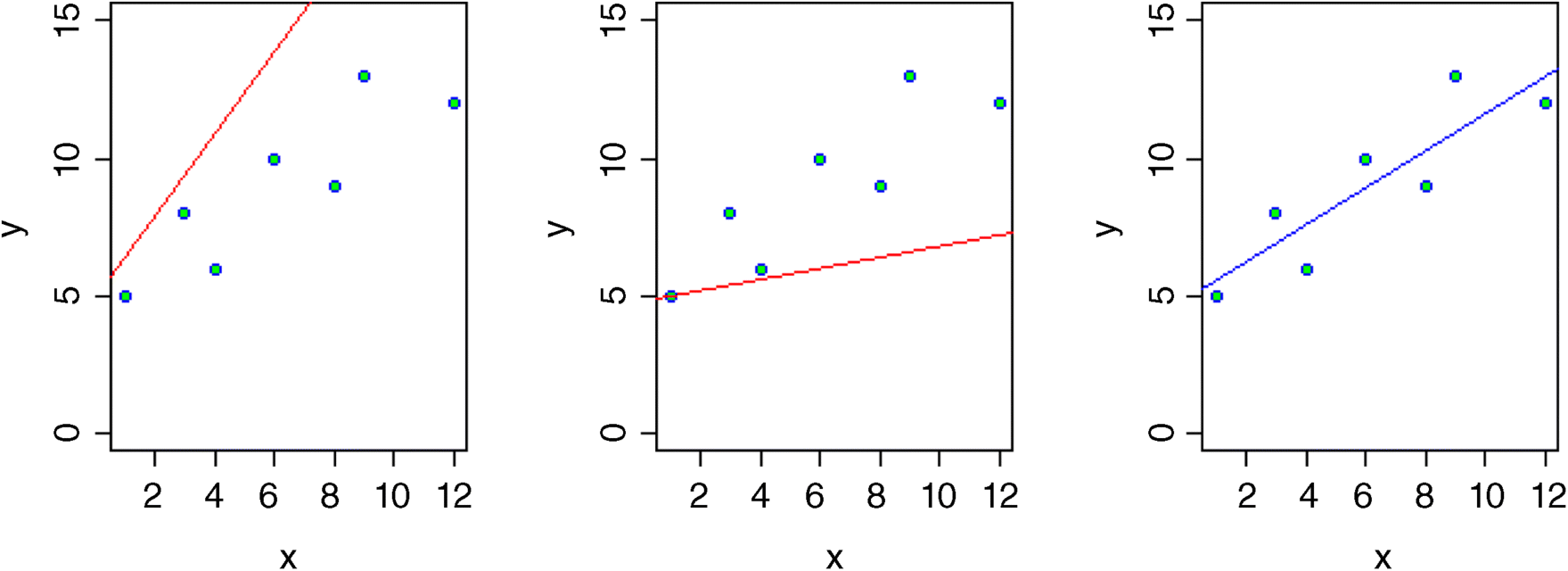
The answer, of course, is no. What about a slope of 0.2 (centre graph)? Again, the data are not at all likely if the graph has such a gentle slope. The maximum likelihood of the data given the model is obtained with a slope of 0.679 (right-hand graph).
This is not how the procedure is carried out in practice, but it makes the point that we judge the model on the basis how likely the data would be if the model were correct. When we do the analysis in earnest, both parameters are estimated simultaneously.
Experimental Design
There are only two key concepts:
- replication
- randomization
You replicate to increase reliability. You randomize to reduce bias. If you replicate thoroughly and randomize properly, you will not go far wrong.
There are a number of other issues whose mastery will increase the likelihood that you analyse your data the right way rather than the wrong way:
- the principle of parsimony
- the power of a statistical test
- controls
- spotting pseudoreplication and knowing what to do about it
- the difference between experimental and observational data (non-orthogonality)
It does not matter very much if you cannot do your own advanced statistical analysis. If your experiment is properly designed, you will often be able to find somebody to help you with the stats. But if your experiment is not properly designed, or not thoroughly randomized, or lacking adequate controls, then no matter how good you are at stats, some (or possibly even all) of your experimental effort will have been wasted. No amount of high-powered statistical analysis can turn a bad experiment into a good one. R is good, but not that good.
The Principle of Parsimony (Occam's Razor)
One of the most important themes running through this book concerns model simplification. The principle of parsimony is attributed to the fourteenth-century English nominalist philosopher William of Occam who insisted that, given a set of equally good explanations for a given phenomenon, then the correct explanation is the simplest explanation. It is called Occam's razor because he ‘shaved’ his explanations down to the bare minimum. In statistical modelling, the principle of parsimony means that:
- models should have as few parameters as possible
- linear models should be preferred to non-linear models
- experiments relying on few assumptions should be preferred to those relying on many
- models should be pared down until they are minimal adequate
- simple explanations should be preferred to complex explanations
The process of model simplification is an integral part of statistical analysis in R. In general, a variable is retained in the model only if it causes a significant increase in deviance when it is removed from the current model. Seek simplicity, then distrust it.
In our zeal for model simplification, we must be careful not to throw the baby out with the bathwater. Einstein made a characteristically subtle modification to Occam's razor. He said: ‘A model should be as simple as possible. But no simpler.’
Observation, Theory and Experiment
There is no doubt that the best way to solve scientific problems is through a thoughtful blend of observation, theory and experiment. In most real situations, however, there are constraints on what can be done, and on the way things can be done, which mean that one or more of the trilogy has to be sacrificed. There are lots of cases, for example, where it is ethically or logistically impossible to carry out manipulative experiments. In these cases it is doubly important to ensure that the statistical analysis leads to conclusions that are as critical and as unambiguous as possible.
Controls
No controls, no conclusions.
Replication: It's the ns that Justify the Means
The requirement for replication arises because if we do the same thing to different individuals we are likely to get different responses. The causes of this heterogeneity in response are many and varied (genotype, age, sex, condition, history, substrate, microclimate, and so on). The object of replication is to increase the reliability of parameter estimates, and to allow us to quantify the variability that is found within the same treatment. To qualify as replicates, the repeated measurements:
- must be independent
- must not form part of a time series (data collected from the same place on successive occasions are not independent)
- must not be grouped together in one place (aggregating the replicates means that they are not spatially independent)
- must be measured at an appropriate spatial scale
- ideally, one replicate from each treatment ought to be grouped together into a block, and all treatments repeated in many different blocks.
- repeated measures (e.g. from the same individual or the same spatial location) are not replicates (this is probably the commonest cause of pseudoreplication in statistical work)
How Many Replicates?
The usual answer is ‘as many as you can afford’. An alternative answer is 30. A very useful rule of thumb is this: a sample of 30 or more is a big sample, but a sample of less than 30 is a small sample. The rule doesn't always work, of course: 30 would be derisively small as a sample in an opinion poll, for instance. In other circumstances, it might be impossibly expensive to repeat an experiment as many as 30 times. Nevertheless, it is a rule of great practical utility, if only for giving you pause as you design your experiment with 300 replicates that perhaps this might really be a bit over the top. Or when you think you could get away with just five replicates this time.
There are ways of working out the replication necessary for testing a given hypothesis (these are explained below). Sometimes we know little or nothing about the variance of the response variable when we are planning an experiment. Experience is important. So are pilot studies. These should give an indication of the variance between initial units before the experimental treatments are applied, and also of the approximate magnitude of the responses to experimental treatment that are likely to occur. Sometimes it may be necessary to reduce the scope and complexity of the experiment, and to concentrate the inevitably limited resources of manpower and money on obtaining an unambiguous answer to a simpler question. It is immensely irritating to spend three years on a grand experiment, only to find at the end of it that the response is only significant at p = 0.08. A reduction in the number of treatments might well have allowed an increase in replication to the point where the same result would have been unambiguously significant.
Power
The power of a test is the probability of rejecting the null hypothesis when it is false. It has to do with Type II errors: ![]() is the probability of accepting the null hypothesis when it is false. In an ideal world, we would obviously make
is the probability of accepting the null hypothesis when it is false. In an ideal world, we would obviously make ![]() as small as possible. But there is a snag. The smaller we make the probability of committing a Type II error, the greater we make the probability of committing a Type I error, and rejecting the null hypothesis when, in fact, it is correct. A compromise is called for. Most statisticians work with
as small as possible. But there is a snag. The smaller we make the probability of committing a Type II error, the greater we make the probability of committing a Type I error, and rejecting the null hypothesis when, in fact, it is correct. A compromise is called for. Most statisticians work with ![]() and
and ![]() . Now the power of a test is defined as
. Now the power of a test is defined as ![]() under the standard assumptions. This is used to calculate the sample sizes necessary to detect a specified difference when the error variance is known (or can be guessed at).
under the standard assumptions. This is used to calculate the sample sizes necessary to detect a specified difference when the error variance is known (or can be guessed at).
Let's think about the issues involved with power analysis in the context of a Student's t-test to compare two sample means. As explained on p. 91, the test statistic is t = difference/(the standard error of the difference) and we can rearrange the formula to obtain n, the sample size necessary in order that that a given difference, d, is statistically significant:
You can see that the larger the variance s2, and the smaller the size of the difference, the bigger the sample we shall need. The value of the test statistic t depends on our decisions about Type I and Type II error rates (conventionally 0.05 and 0.2). For sample sizes of order 30, the t values associated with these probabilities are 1.96 and 0.84 respectively: these add to 2.80, and the square of 2.80 is 7.84. To the nearest whole number, the constants in the numerator evaluate to 2 × 8 = 16. So as a good rule of thumb, the sample size you need in each treatment is given by
We simply need to work out 16 times the sample variance (obtained from the literature or from a small pilot experiment) and divide by the square of the difference that we want to be able to detect. So suppose that our current cereal yield is 10 t/ha with a standard deviation of sd = 2.8 t/ha (giving s2 = 7.84) and we want to be able to say that a yield increase (delta) of 2 t/ha is significant at 95% with power = 80%, then we shall need to have 16 × 7.84/4 = 31.36 replicates in each treatment. The built in R function
power.t.test(delta=2,sd=2.8,power=0.8)also gives n = 32 replicates per treatment on rounding-up.
Randomization
Randomization is something that everybody says they do, but hardly anybody does properly. Take a simple example. How do I select one tree from a forest of trees, on which to measure photosynthetic rates? I want to select the tree at random in order to avoid bias. For instance, I might be tempted to work on a tree that had accessible foliage near to the ground, or a tree that was close to the lab. Or a tree that looked healthy. Or a tree that had nice insect-free leaves. And so on. I leave it to you to list the biases that would be involved in estimating photosynthesis on any of those trees.
One common way of selecting a ‘random’ tree is to take a map of the forest and select a random pair of coordinates (say 157 m east of the reference point, and 228 m north). Then pace out these coordinates and, having arrived at that particular spot in the forest, select the nearest tree to those coordinates. But is this really a randomly selected tree?
If it were randomly selected, then it would have exactly the same chance of being selected as every other tree in the forest. Let us think about this. Look at the figure below, which shows a map of the distribution of trees on the ground. Even if they were originally planted out in regular rows, accidents, tree-falls, and heterogeneity in the substrate would soon lead to an aggregated spatial distribution of trees. Now ask yourself how many different random points would lead to the selection of a given tree. Start with tree (a). This will be selected by any points falling in the large shaded area.
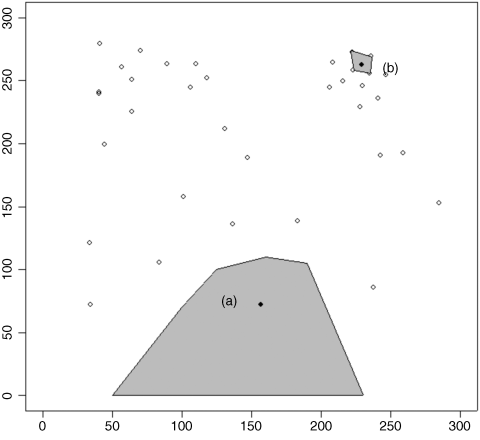
Now consider tree (b). It will only be selected if the random point falls within the tiny area surrounding that tree. Tree (a) has a much greater chance of being selected than tree (b), and so the nearest tree to a random point is not a randomly selected tree. In a spatially heterogeneous woodland, isolated trees and trees on the edges of clumps will always have a higher probability of being picked than trees in the centre of clumps.
The answer is that to select a tree at random, every single tree in the forest must be numbered (all 24 683 of them, or whatever), and then a random number between 1 and 24 683 must be drawn out of a hat. There is no alternative. Anything less than that is not randomization.
Now ask yourself how often this is done in practice, and you will see what I mean when I say that randomization is a classic example of ‘Do as I say, and not do as I do’. As an example of how important proper randomization can be, consider the following experiment that was designed to test the toxicity of five contact insecticides by exposing batches of flour beetles to the chemical on filter papers in Petri dishes. The animals walk about and pick up the poison on their feet. The Tribolium culture jar was inverted, flour and all, into a large tray, and beetles were collected as they emerged from the flour. The animals were allocated to the five chemicals in sequence; three replicate Petri dishes were treated with the first chemical, and 10 beetles were placed in each Petri dish. Do you see the source of bias in this procedure?
It is entirely plausible that flour beetles differ in their activity levels (sex differences, differences in body weight, age, etc.). The most active beetles might emerge first from the pile of flour. These beetles all end up in the treatment with the first insecticide. By the time we come to finding beetles for the last replicate of the fifth pesticide, we may be grubbing round in the centre of the pile, looking for the last remaining Tribolium. This matters, because the amount of pesticide picked by the beetles up will depend upon their activity levels. The more active the beetles, the more chemical they pick up on their feet, and the more likely they are to die. Thus, the failure to randomize will bias the result in favour of the first insecticide because this treatment received the most active beetles.
What we should have done is this. If we think that insect activity level is important in our experiment, then we should take this into account at the design stage. We might decide to have three levels of activity: active, average and sluggish. We fill the first five Petri dishes with 10 each of the active insects that emerge first from the pile. The next 50 insects we find go 10-at-a-time into five Petri dishes that are labelled average. Finally, we put last 50 insects to emerge into a set of five Petri dishes labelled sluggish. This procedure has created three blocks based on activity levels: we do not know precisely why the insects differed in their activity levels, but we think it might be important. Activity level is called a random effect: it is a factor with three levels. Next comes the randomization. We put the names of the five insecticides into a hat, shuffle them up, and draw them out one-at-a-time at random. The first Petri dish containing active beetles receives the insecticide that is first out of the hat, and so on until all five active Petri dishes have been allocated their own different pesticide. Then the five labels go back in the hat and are reshuffled. The procedure is repeated to allocate insecticide treatment at random to the five average activity Petri dishes. Finally, we put the labels back in the hat and draw the insecticide treatment for the five Petri dishes containing sluggish insects.
But why go to all this trouble? The answer is very important, and you should read it again and again until you understand it. The insects differ and the insecticides differ. But the Petri dishes may differ, too, especially if we store them in slightly different circumstances (e.g. near to the door of the controlled temperature cabinet or away at the back of the cabinet). The point is that there will be a total amount of variation in time to death across all the insects in the whole experiment (all 3 × 5 × 10 = 150 of them). We want to partition this variation into that which can be explained by differences between the insecticides and that which cannot.
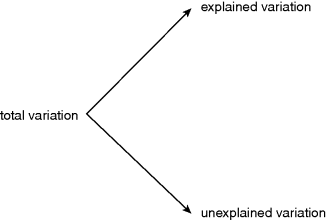
If the amount of variation explained by differences between the insecticide treatments is large, then we conclude that the insecticides are significantly different from one another in their effects on mean age at death. We make this judgement on the basis of a comparison between the explained variation SSA and the unexplained variation SSE. If the unexplained variation is large, it is going to be very difficult to conclude anything about our fixed effect (insecticide in this case).
The great advantage of blocking is that it reduces the size of the unexplained variation. In our example, if activity level had a big effect on age at death (block variation), then the unexplained variation SSE would be much smaller than would have been the case if we had ignored activity and the significance of our fixed effect will be correspondingly higher:
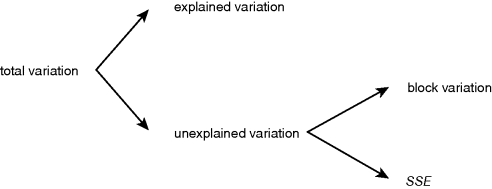
The idea of good experimental design is to make SSE as small as possible, and blocking is the most effective way to bring this about.
R is very useful during the randomization stage because it has a function called sample which can shuffle the factor levels into a random sequence. Put the names of the five insecticides into a vector like this:
treatments <- c("aloprin","vitex","formixin","panto","allclear")Then use sample to shuffle them for the active insects in dishes 1 to 5:
sample(treatments)[1] "formixin" "panto" "vitex" "aloprin" "allclear"then for the insects with average activity levels in dishes 6 to 10:
sample(treatments)[1] "formixin" "allclear" "aloprin" "panto" "vitex" then finally for the sluggish ones in dishes 11 to 15:
sample(treatments)[1] "panto" "aloprin" "allclear" "vitex" "formixin"The recent trend towards ‘haphazard’ sampling is a cop-out. What it means is that ‘I admit that I didn't randomize, but you have to take my word for it that this did not introduce any important biases’. You can draw your own conclusions.
Strong Inference
One of the most powerful means available to demonstrate the accuracy of an idea is an experimental confirmation of a prediction made by a carefully formulated hypothesis. There are two essential steps to the protocol of strong inference (Platt, 1964):
- formulate a clear hypothesis
- devise an acceptable test
Neither one is much good without the other. For example, the hypothesis should not lead to predictions that are likely to occur by other extrinsic means. Similarly, the test should demonstrate unequivocally whether the hypothesis is true or false.
A great many scientific experiments appear to be carried out with no particular hypothesis in mind at all, but simply to see what happens. While this approach may be commendable in the early stages of a study, such experiments tend to be weak as an end in themselves, because there will be such a large number of equally plausible explanations for the results. Without contemplation there will be no testable predictions; without testable predictions there will be no experimental ingenuity; without experimental ingenuity there is likely to be inadequate control; in short, equivocal interpretation. The results could be due to myriad plausible causes. Nature has no stake in being understood by scientists. We need to work at it. Without replication, randomization and good controls we shall make little progress.
Weak Inference
The phrase ‘weak inference’ is used (often disparagingly) to describe the interpretation of observational studies and the analysis of so-called ‘natural experiments’. It is silly to be disparaging about these data, because they are often the only data that we have. The aim of good statistical analysis is to obtain the maximum information from a given set of data, bearing the limitations of the data firmly in mind.
Natural experiments arise when an event (often assumed to be an unusual event, but frequently without much justification of what constitutes unusualness) occurs that is like an experimental treatment (a hurricane blows down half of a forest block; a landslide creates a bare substrate; a stock market crash produces lots of suddenly poor people, etc.). ‘The requirement of adequate knowledge of initial conditions has important implications for the validity of many natural experiments. Inasmuch as the “experiments” are recognized only when they are completed, or in progress at the earliest, it is impossible to be certain of the conditions that existed before such an “experiment” began. It then becomes necessary to make assumptions about these conditions, and any conclusions reached on the basis of natural experiments are thereby weakened to the point of being hypotheses, and they should be stated as such’ (Hairston, 1989).
How Long to Go On?
Ideally, the duration of an experiment should be determined in advance, lest one falls prey to one of the twin temptations:
- to stop the experiment as soon as a pleasing result is obtained
- to keep going with the experiment until the ‘right’ result is achieved (the ‘Gregor Mendel effect’)
In practice, most experiments probably run for too short a period, because of the idiosyncrasies of scientific funding. This short-term work is particularly dangerous in medicine and the environmental sciences, because the kind of short-term dynamics exhibited after pulse experiments may be entirely different from the long-term dynamics of the same system. Only by long-term experiments of both the pulse and the press kind will the full range of dynamics be understood. The other great advantage of long-term experiments is that a wide range of patterns (e.g. ‘kinds of years’) is experienced.
Pseudoreplication
Pseudoreplication occurs when you analyse the data as if you had more degrees of freedom than you really have. There are two kinds of pseudoreplication:
- temporal pseudoreplication, involving repeated measurements from the same individual
- spatial pseudoreplication, involving several measurements taken from the same vicinity
Pseudoreplication is a problem because one of the most important assumptions of standard statistical analysis is independence of errors. Repeated measures through time on the same individual will have non-independent errors because peculiarities of the individual will be reflected in all of the measurements made on it (the repeated measures will be temporally correlated with one another). Samples taken from the same vicinity will have non-independent errors because peculiarities of the location will be common to all the samples (e.g. yields will all be high in a good patch and all be low in a bad patch).
Pseudoreplication is generally quite easy to spot. The question to ask is this. How many degrees of freedom for error does the experiment really have? If a field experiment appears to have lots of degrees of freedom, it is probably pseudoreplicated. Take an example from pest control of insects on plants. There are 20 plots, 10 sprayed and 10 unsprayed. Within each plot there are 50 plants. Each plant is measured five times during the growing season. Now this experiment generates 20 × 50 × 5 = 5000 numbers. There are two spraying treatments, so there must be 1 degree of freedom for spraying and 4998 degrees of freedom for error. Or must there? Count up the replicates in this experiment. Repeated measurements on the same plants (the five sampling occasions) are certainly not replicates. The 50 individual plants within each quadrat are not replicates either. The reason for this is that conditions within each quadrat are quite likely to be unique, and so all 50 plants will experience more or less the same unique set of conditions, irrespective of the spraying treatment they receive. In fact, there are 10 replicates in this experiment. There are 10 sprayed plots and 10 unsprayed plots, and each plot will yield only one independent datum to the response variable (the proportion of leaf area consumed by insects, for example). Thus, there are 9 degrees of freedom within each treatment, and 2 × 9 = 18 degrees of freedom for error in the experiment as a whole. It is not difficult to find examples of pseudoreplication on this scale in the literature (Hurlbert, 1984). The problem is that it leads to the reporting of masses of spuriously significant results (with 4998 degrees of freedom for error, it is almost impossible not to have significant differences). The first skill to be acquired by the budding experimenter is the ability to plan an experiment that is properly replicated.
There are various things that you can do when your data are pseudoreplicated:
- average away the pseudoreplication and carry out your statistical analysis on the means
- carry out separate analyses for each time period
- use more advanced statistical techniques such as time series analysis or mixed effects models
Initial Conditions
Many otherwise excellent scientific experiments are spoiled by a lack of information about initial conditions. How can we know if something has changed if we do not know what it was like to begin with? It is often implicitly assumed that all the experimental units were alike at the beginning of the experiment, but this needs to be demonstrated rather than taken on faith. One of the most important uses of data on initial conditions is as a check on the efficiency of randomization. For example, you should be able to run your statistical analysis to demonstrate that the individual organisms were not significantly different in mean size at the beginning of a growth experiment. Without measurements of initial size, it is always possible to attribute the end result to differences in initial conditions. Another reason for measuring initial conditions is that the information can often be used to improve the resolution of the final analysis through analysis of covariance (see Chapter 9).
Orthogonal Designs and Non-Orthogonal Observational Data
The data in this book fall into two distinct categories. In the case of planned experiments, all of the treatment combinations are equally represented and, barring accidents, there will be no missing values. Such experiments are said to be orthogonal. In the case of observational studies, however, we have no control over the number of individuals for which we have data, or over the combinations of circumstances that are observed. Many of the explanatory variables are likely to be correlated with one another, as well as with the response variable. Missing treatment combinations will be commonplace, and such data are said to be non-orthogonal. This makes an important difference to our statistical modelling because, in orthogonal designs, the variability that is attributed to a given factor is constant, and does not depend upon the order in which that factor is removed from the model. In contrast, with non-orthogonal data, we find that the variability attributable to a given factor does depend upon the order in which the factor is removed from the model. We must be careful, therefore, to judge the significance of factors in non-orthogonal studies, when they are removed from the maximal model (i.e. from the model including all the other factors and interactions with which they might be confounded). Remember, for non-orthogonal data, order matters.
Aliasing
This topic causes concern because it manifests itself as one or more rows of NA appearing unexpectedly in the output of your model. Aliasing occurs when there is no information on which to base an estimate of a parameter value. Intrinsic aliasing occurs when it is due to the structure of the model. Extrinsic aliasing occurs when it is due to the nature of the data. Parameters can be aliased for one of two reasons:
- there are no data in the dataframe from which to estimate the parameter (e.g. missing values, partial designs or correlation amongst the explanatory variables)
- the model is structured in such a way that the parameter value cannot be estimated (e.g. over-specified models with more parameters than necessary)
If we had a factor with four levels (say none, light, medium and heavy use) then we could estimate four means from the data, one for each factor level. But the model looks like this:
where the xi are dummy variables having the value 0 or 1 for each factor level (see p. 158), the ![]() are the effect sizes and μ is the overall mean. Clearly there is no point in having five parameters in the model if we can estimate only four independent terms from the data. One of the parameters must be intrinsically aliased. This topic is explained in detail in Chapter 11.
are the effect sizes and μ is the overall mean. Clearly there is no point in having five parameters in the model if we can estimate only four independent terms from the data. One of the parameters must be intrinsically aliased. This topic is explained in detail in Chapter 11.
In a multiple regression analysis, if one of the continuous explanatory variables is perfectly correlated with another variable that has already been fitted to the data (perhaps because it is a constant multiple of the first variable), then the second term is aliased and adds nothing to the descriptive power of the model. Suppose that x2 = 0.5x1; then fitting a model with x1 + x2 will lead to x2 being intrinsically aliased and given a parameter estimate of NA.
If all of the values of a particular explanatory variable are set to zero for a given level of a particular factor, then that level is said to have been intentionally aliased. This sort of aliasing is a useful programming trick during model simplification in ANCOVA when we wish a covariate to be fitted to some levels of a factor but not to others.
Finally, suppose that in a factorial experiment, all of the animals receiving level 2 of diet (factor A) and level 3 of temperature (factor B) have died accidentally as a result of attack by a fungal pathogen. This particular combination of diet and temperature contributes no data to the response variable, so the interaction term A(2):B(3) cannot be estimated. It is extrinsically aliased, and its parameter estimate is set to NA.
Multiple Comparisons
The thorny issue of multiple comparisons arises because when we do more than one test we are likely to find ‘false positives’ at an inflated rate (i.e. by rejecting a true null hypothesis more often than indicated by the value of ![]() ). The old fashioned approach was to use Bonferroni's correction; in looking up a value for Student's t, you divide your
). The old fashioned approach was to use Bonferroni's correction; in looking up a value for Student's t, you divide your ![]() value by the number of comparisons you have done. If the result is still significant then all is well, but it often will not be. Bonferroni's correction is very harsh and will often throw out the baby with the bathwater. An old-fashioned alternative was to use Duncan's multiple range tests (you may have seen these in old stats books, where lower-case letters were written at the head of each bar in a barplot: bars with different letters were significantly different, while bars with the same letter were not significantly different. The modern approach is to use contrasts wherever possible, and where it is essential to do multiple comparisons, then to use the wonderfully named Tukey's honestly significant differences (see ?TukeyHSD).
value by the number of comparisons you have done. If the result is still significant then all is well, but it often will not be. Bonferroni's correction is very harsh and will often throw out the baby with the bathwater. An old-fashioned alternative was to use Duncan's multiple range tests (you may have seen these in old stats books, where lower-case letters were written at the head of each bar in a barplot: bars with different letters were significantly different, while bars with the same letter were not significantly different. The modern approach is to use contrasts wherever possible, and where it is essential to do multiple comparisons, then to use the wonderfully named Tukey's honestly significant differences (see ?TukeyHSD).
Summary of Statistical Models in R
Models are fitted to data (not the other way round), using one of the following model-fitting functions:
- lm: fits a linear model assuming normal errors and constant variance; generally this is used for regression analysis using continuous explanatory variables. The default output is summary.lm
- aov: an alternative to lm with summary.aov as the default output. Typically used only when there are complex error terms to be estimated (e.g. in split-plot designs where different treatments are applied to plots of different sizes)
- glm: fits generalized linear models to data using categorical or continuous explanatory variables, by specifying one of a family of error structures (e.g. Poisson for count data or binomial for proportion data) and a particular link function
- gam: fits generalized additive models to data with one of a family of error structures (e.g. Poisson for count data or binomial for proportion data) in which the continuous explanatory variables can (optionally) be fitted as arbitrary smoothed functions using non-parametric smoothers rather than specific parametric functions.
- lmer: fits linear mixed effects models with specified mixtures of fixed effects and random effects and allows for the specification of correlation structure amongst the explanatory variables and autocorrelation of the response variable (e.g. time series effects with repeated measures). The older lme is an alternative
- nls: fits a non-linear regression model via least squares, estimating the parameters of a specified non-linear function
- nlme: fits a specified non-linear function in a mixed effects model where the parameters of the non-linear function are assumed to be random effects; allows for the specification of correlation structure amongst the explanatory variables and autocorrelation of the response variable (e.g. time series effects with repeated measures).
- loess: fits a local regression model with one or more continuous explanatory variables using non-parametric techniques to produce a smoothed model surface
- rpart: fits a regression tree model using binary recursive partitioning whereby the data are successively split along coordinate axes of the explanatory variables so that at any node, the split is chosen that maximally distinguishes the response variable in the left and the right branches. With a categorical response variable, the tree is called a classification tree, and the model used for classification assumes that the response variable follows a multinomial distribution
For most of these models, a range of generic functions can be used to obtain information about the model. The most important and most frequently used are
| summary | produces parameter estimates and standard errors from lm, and ANOVA tables from aov; this will often determine your choice between lm and aov. For either lm or aov you can choose summary.aov or summary.lm to get the alternative form of output (an ANOVA table or a table of parameter estimates and standard errors; see p. 158) |
| plot | produces diagnostic plots for model checking, including residuals against fitted values, influence tests, etc. |
| anova | a useful function for comparing two or more different models and producing ANOVA tables (and alternative to AIC) |
| update | used to modify the last model fit; it saves both typing effort and computing time |
Other useful generics include:
| coef | the coefficients (estimated parameters) from the model |
| fitted | the fitted values, predicted by the model for the values of the explanatory variables that appear in the data frame |
| resid | the residuals (the differences between measured and predicted values of y) |
| predict | uses information from the fitted model to produce smooth functions for plotting a curve through the scatterplot of your data. The trick is to realize that you need to provide values for all of the explanatory variables that are in the model (both continuous and categorical) as a list, and that the vectors of explanatory variables must all be exactly the same length (see p. 248 for a worked example). You can back-transform automatically using the option type="response". |
Organizing Your Work
There are three things that you really must keep for each separate R session:
- the dataframe, stored in a comma-delimited (.csv) or a tab-delimited (.txt) file
- the script, stored in a text file (.txt)
- the results obtained during this session (tables, graphs, model objects, etc.) stored in a PDF so that you can retain the graphics along with model outputs
To make sure you remember which data files and results go with which scripts, it is good practice to save the script, results and data files in the same, sensibly named folder.
Once the data are checked and edited, you are not likely ever to want to alter the data file. On the other hand, you are likely to want to keep a separate script for each working session of R. One of the great advantages of using scripts is that you can copy (potentially large) sections of code from previous successful sessions and save yourself a huge amount of typing (and wheel reinvention).
There are two sensible ways of working and you should choose the one that suits you best. The first is to write all of your code in a script editor, save it regularly, and pepper it liberally with comments (use the hatch symbol to start each comment):
# this is a commentWhen you make mistakes, cut them out of the script, taking care not to delete important bits of code accidentally.
The alternative is to save the script of the whole session just before you finish. This is stored in what R calls the history file. At the end of the session, type
history(Inf)and R will open a script window called ‘R History’ containing a full transcript of all the commands (both right and wrong) that you entered during that session. Copy all the material to a text file, edit out the mistakes (again, making sure that you do not remove any essential lines of code), add the necessary comments, then save the text file as your script for the session in its customized directory along with the data file and the results (the output of tables, models and graphics).
Whichever method you use, the saved script is a permanent record of what you did (with comments pointing out exactly why you did it). You are likely to copy and paste the code into R on future occasions when you want to do similar analyses, and you want the code to work seamlessly (which it will not do if you have unintentionally removed key lines of code).
It is a bad idea to create your scripts in a word processor because several of the symbols you will use may not be readable within R. Double quotes is a classic example of this; your word processor will have “ (open quotes) and ” (close quotes) but R will read only " (simple quotes). However, you might want to save the results from your R sessions in a word processor because this can include graphs as well as input and output in the same document.
Housekeeping within R
The simplest way to work is to start a new R session for each separate activity. The advantage of working this way is that things from one session do not get mixed up with things from another session.
The classic thing to go wrong is that you get two different objects with the same name, and you do not know which is which. For instance, a variable called x from one analysis may contain 30 numbers and a different variable called x from another analysis might have 50 numbers in it. At least, in that case, you can test the length of the object to see which one it is (if it is of length 50 then it must be the x variable from the second analysis). Worse problems arise when the two different variables called x are both the same length. Then you really do not know where you are.
If you insist on doing several things during the same R session, then it pays to be really well organized. In this book we attach dataframes, so that you can refer to your variables by name without reference to the name of the dataframe from which they come (experts generally do not use attach). The disadvantage of using attach is that you might have several dataframes attached that contain exactly the same variable name. R will warn you of this by writing
The following object is masked from first.frame:temp, windwhen you attach a dataframe containing variables that are already attached from a different dataframe. The message means that when you attached a new dataframe, it contained two variables, called temp and wind respectively, that were already attached from a previous dataframe called first.frame. This state of affairs is confusing and unsatisfactory. The way to avoid it is to make sure that you detach all unnecessary dataframes before attaching a new dataframe. Here is the problem situation in full:
first.frame <- read.csv("c:\temp\test.pollute.csv")second.frame <- read.csv("c:\temp\ozone.data.csv")attach(first.frame)attach(second.frame)The following object is masked from first.frame:temp, wind
Here is how to avoid the problem
first.frame <- read.csv("c:\temp\test.pollute.csv")second.frame <- read.csv("c:\temp\ozone.data.csv")attach(first.frame)
. . . this is where you work on the information from first.frame. Then when you are finished . . .
detach(first.frame)attach(second.frame)
No warning message is printed because temp and rain are no longer duplicate variable names.
The other big problem arises when you create variables during a session by allocation (this typically involves calculation or the use of data-generating functions within R to produce random numbers, for instance, or sequences). So if in the first session you wanted x to be ![]() then you would put:
then you would put:
x <- sqrt(2)Now, in a later session you use x for the axis of a graph, and give it the sequence of values 0 to 10:
x <- 0:10If the fact that you had done this slipped your mind, then you might later use x thinking that is was the single number ![]() . But R knows it to be the vector of 11 numbers 0 to 10, and this could have seriously bad consequences. The way to avoid problems like this is to remove all the variables you have calculated before you start on another project during the same session of R. The function for this is rm (or remove)
. But R knows it to be the vector of 11 numbers 0 to 10, and this could have seriously bad consequences. The way to avoid problems like this is to remove all the variables you have calculated before you start on another project during the same session of R. The function for this is rm (or remove)
rm(x)If you ask for a variable to be removed that does not exist, then R will warn you of this fact:
rm(y,z)Warning messages:1: In rm(y, z) : object 'y' not found2: In rm(y, z) : object 'z' not found
We are now in a position to start using R in earnest. The first thing to learn is how to structure a dataframe and how to read a dataframe into R. It is immensely irritating that this first step often turns out to be so difficult for beginners to get right. Once the data are into R, the rest is plain sailing.
References
- Hairston, N.G. (1989) Ecological Experiments: Purpose, Design and Execution, Cambridge University Press, Cambridge.
- Hurlbert, S.H. (1984) Pseudoreplication and the design of ecological field experiments. Ecological Monographs, 54, 187–211.
- Platt, J.R. (1964) Strong inference. Science, 146, 347–353.
Further Reading
- Atkinson, A.C. (1985) Plots, Transformations, and Regression, Clarendon Press, Oxford.
- Box, G.E.P., Hunter, W.G. and Hunter, J.S. (1978) Statistics for Experimenters: An Introduction to Design, Data Analysis and Model Building, John Wiley & Sons, New York.
- Chambers, J.M., Cleveland, W.S., Kleiner, B. and Tukey, P.A. (1983) Graphical Methods for Data Analysis, Wadsworth, Belmont, CA.
- Winer, B.J., Brown, D.R. and Michels, K.M. (1991) Statistical Principles in Experimental Design, McGraw-Hill, New York.
