The motivation for domain interactions is that decisions made locally in one domain can have impacts on system-level requirements and other domain-specific requirements. For example, heat dissipation is typically not thought of as a constraint that is impacted by the choice of a software algorithm. Unfortunately, software execution can dramatically impact heat dissipation through its interaction with the CPU it runs on, and indirectly through interfaces to other system components. Other examples include impacts of local power consumption on system-level power constraints, impacts of component function on system security, and impacts of electromagnetic interference among chips on a board. In each case, local decisions impact the overall system.
Rosetta defines an interaction as a collection of mechanisms for describing how information flows between modeling domains. Each interaction defines three kinds of information transfer. Translators define how information is transformed as it flows through a parameter shared by two facets. Translators handle both information translation and coordination of the communication process. Functors define transformations of facets from one domain to another. Because facets are simply Rosetta values, these transformations take the form of functions whose domain and range include facet types. Algebra combinators, or simply combinators, define mechanisms for combining two facets to produce a new facet. Combinators are like functors, except that the domain of a combinator must include two facets that will be composed into a single facet.
Projection functions, functors, and combinators are the Rosetta constructs used to define interactions. Projection functions transform a facet into another form, such as a calculated value. They are used to project values from one domain to another. Functors are specialized projection functions that transform a facet into a new facet in a potentially different domain. They are used to move models between domains to facilitate composition, analysis, and reuse. Finally, combinators take multiple facets and transform them into new facets. They are used specifically for facet composition and frequently involve product and sum operations.
Projection functions, functors, and combinators all treat Rosetta specification elements as data. They must examine the structure of facets and in most cases generate new facets. To facilitate this, Rosetta provides the special-purpose constructors, observers, and templates to observe and construct Rosetta abstract syntax elements (described in Chapter 12). Projection functions, functors, and combinators all examine the structure of a facet using observers and create new facet abstract syntax elements using constructors and template expressions. Thus, the same syntactic and semantic structures used for domain specification are used for facet manipulation.
A projection function moves information from one domain to another. All projection functions transform a source facet and a destination facet into a collection of terms in the domain of the destination facet. Effectively, the projection function moves information from the source domain into the destination domain specific to the two facets involved. Specifically, the signature of a projection function has the following form:
P(S::DS,D::DD)::term_list;
where P names the projection function. Here S is the source facet from domain DS and D is the destination facet from domain DD; both must be facets, but the associated parameter type may be a subtype of the general facet type. A projection function is in all ways a traditional Rosetta function and is defined using the same techniques. What distinguishes a project function is the presence of a facet type in the argument list.
Example 15.1. A Projection Function
The transform_terms projection function takes a facet from the static domain and transforms its terms into terms appropriate for use in the state_based domain by asserting that each is true in any state. The helper function transform_term takes a single term and asserts that it is true for all states using a universal quantifier and the ticked expression at:
transform_term(x::term)::term is << term forall(st::state |'x' 'at(st)) >>
The transform_terms projection function uses the transform_term function to transform its collection of terms into terms for the state_based domain:
transform_terms(F::static)::set(term) is image(transform_term,terms(F));
While a projection function usually moves information from one facet to another, a morphism is a function that generates an entirely new facet. In addition to generating new terms, a morphism is responsible for generating parameter lists, variable sets, and export lists, and for selecting a domain for the new facet. Where a projection function moves information from one facet to another, a morphism generates one facet from another.
A functor is a special morphism that can operate on any facet in a domain. While morphisms may be specific to a particular facet, a functor maps every facet from one type into a facet from another. In essence, a functor generalizes a collection of morphisms to operate over a collection of facets. Functors are heavily used when moving specifications up and down the domain semi-lattice as well as when moving them between arbitrary domains.
One definition mechanism for morphisms is to define functions that construct new facets using template expressions. Using this approach, a traditional function is written that fills in a template expression, much like a constructed type to generate the new facet. The template expression would have the following form:
<< complete_facet_declaration facet 'name' 'signature' is 'exports' 'declarations' begin 'terms' end facet 'name' >>
where name, signature, exports, declarations, and terms are replaced by functions that generate the new abstract syntax or will be processed as a part of the template expression.
The second mechanism for constructing a new facet calls the facet constructor directly. The previous facet can be defined directly as:
make_complete_facet_declaration(name,signature,exports,declarations,terms)
The result is exactly the same AST structure as is generated by the template. The template example uses the template expression to take advantage of concrete syntax, with the advantage being a definition that is frequently easier to read. The function example uses the facet constructor to avoid the template expression completely, preferring to construct each AST structure. The choice is purely stylistic. When most of the elements of a construct are generated with functions, using the constructor is most appropriate. Otherwise, the template approach is preferred.
Example 15.2. Functor for Moving static Facets into the state_based Domain
The gamma functor defined below uses the translate_terms function to translate a static facet into a state_based facet. The template for creating facets is instantiated for this specific case. Declarations and exports remain the same in the new facet. Terms are generated from the original terms using the previously defined translator function. Finally, a new name and signature must be defined for the new facet.
gamma(F::static)::state_based is let new_name :: facet_name be mangle(name(F)); new_sig :: facet_signature be convert_sig(signature(F)) in << complete_facet_declaration facet 'new_name' 'new_sig' is 'exports(F)' 'declarations(F)' begin 'translate_terms(F)' end facet 'new_name' >> end let;
The utility functions mangle and convert_sig are defined to create a new facet name and a new signature, replacing static with state_based as the facet type. Their complete definitions are omitted for brevity.
A combinator is a functor that takes two facets and transforms them into a third facet. The purpose of any combinator is to compose specifications for analysis or further refinement. Combinators are defined much like morphisms, with the exception that they take two facet arguments. Like morphisms, combinators can be defined using template expressions and direct calls to facet constructor functions. Using sums and products of facets provides a third mechanism in addition to templates and constructors.
The primary use for combinator is to provide a capability for composing and refining or abstracting two facets in a single step. For example, a combinator could be used to take a power consumption specification and a functional specification for a digital component and generate a single simulation model that examines both. This can be done by using one or more functors and a facet product, but these operations are so common in Rosetta specifications that using the combinator to encapsulate the operations into a functor can simplify and improve the specification.
Example 15.3. Combinator for Composing discrete_time Specifications into Simulatable Models
A simple example of a combinator is the concretization combinator that composes two discrete_time facets into a single discrete event simulation (des) facet. The operation simply uses the concretization function, gamma, from the interaction between discrete_time and des to move each model to the des domain. Then a product operation composes them into a single model:
gammaC(x::discrete_time y::discrete_time)::des ; is discrete_time_des.gamma(x) * discrete_time_des.gamma(y);
The effect of this combinator is to compose two discrete_time models into a single simulatable model. This combinator is useful for composing requirements models and functional models to determine if requirements are met by an implementation.
Rosetta interactions are less monolithic “things” than they are collections of information that define moving information between domains. Interactions are defined using a syntactic form that packages the various mechanisms for domain interaction. As such, each interaction defines translators, functors, and combinators between two domains. The syntax for defining an interaction is as follows:
interaction name(parameters) between D1 and D2 [[ as D3 ]] is [[ export exportList | all ]]; localDecls begin begin translators [[ translatorDecls ]] end translators; begin functors [[ functorDecls ]] end functors begin combinators [[ combinatorDecls ]] end combinators; end interaction name;
In this definition, D1 and D2 are the source domains for models. The optional D3 value is the common supertype of D1 and D2 for forming products and sums using the * and + operation. The default value for D3 is the greatest common supertype of D1 and D2. It is possible that D1 = D2 in situations where translators must lift values from included facets into facets of the same type. Functors may also be written in such interactions, but the identity functor will suffice in most cases. Parameters defined for an interaction are of kind design similar to package parameters. Interaction parameters are used like generics to configure a general-purpose interaction for a specific use. However, interaction parameters are rarely used in practice.
All items defined an interaction’s translators, functors, and combinators blocks are implicitly exported, the only exception being locally defined items appearing in the declarative region of each block. Such declarations must be constants and cannot be exported. Items declared in the interaction’s declarative region are exported. The similarity between interaction definitions and package definitions is not accidental: both encapsulate related definitions. Where declarations in packages may be related for any number of reasons, declarations in interactions always define information flow between their associated domains.
name(parameters) from x:: Tsrc in Dsrc to Tdest in Ddest [[ is expression]] [[ where expression]];
Dsrc is the source domain and Ddest is the destination domain; both must be either D1 or D2 defined in the interaction header. Tsrc and Tdest are the source and destination types; they will frequently be the same. The x parameter is for use in the translator definition, and expression is an expression of type Tdest that transforms x into a new value defined in Ddest. The value of an translator is not a function value, but defines a transformation to perform on parameters as a tick operator.
The is and where classes behave as they would in traditional function definitions. Both can be excluded to define a variable translator or translator signature. Thus, the signature of a translator can be defined without providing additional details.
name(parameters) from x:: Dsrc to Ddest [[ is expression]] [[ where expression]];
Functor definition is nearly identical to translator definition, except that the x parameter is a facet of type Dsrc rather than a value defined in that domain. The functor is in all ways a function, with syntactic sugar added to the definition to enhance readability and to help correct functor definition.
name(parameters) from x::Dsrc1 and y::Dsrc2 to Ddest [[ is expression]] [[ where expression]];
Combinator definition is nearly identical to functor definition, except the x and y parameters represent facets from the two source domains rather than from a single source domain. The combinator is in all ways a function, with syntactic sugar added to the definition to enhance readability and to correct combinator specification.
It should be noted that functors and combinators can be defined outside the structure of an interaction definition. They are simply functions that operate on language elements rather than on traditional data. It is perfectly reasonable to have a function with the signature:
morph(f::state_based)::finite_state;
<* (f::state_based)::finite_state *>
All operations on functions apply equally to functors and combinators, including currying and composition. Because translators are not traditional functions, such operations cannot be legally applied to them. For the same reason, translators are not easily defined outside the scope of an interaction. They can be defined as a part of functors and combinators as well as with clauses in domain definitions.
It is unwieldy to specify interaction elements whenever they are used in a specification. This is particularly true of translators that can clutter interfaces and reduce readability. Thus, the use clause defines default interactions for a given specification. An interaction is specified in a use clause in the same manner as a package is. The interaction is named and parameters are specified when required:
use name(p0, p1,..., pn);
The use clause identifies specific interaction definitions in the same manner as for packages, using the dot notation to identify the library where the interaction exists:
use p0. p1...name(v0, v1,..., vn);
where pk are package or library names and vk are values for interaction parameters.
A specific element of an interaction can be used by identifying it in the use clause:
use p0. p1...name(v0, v1,..., vn). n;
where n is the name of a functor, translator, or combinator function defined in the interaction.
When an interaction is used by a package, the export clause defined in the interaction controls visibility in the same manner as for a package. The only distinction is that for translators, the translator domains are used to select a translator when none is explicitly defined. Specifically, if a facet Fsrc:: Dsrc is included in a facet Fdest:: Ddest and translators are not specified for parameters of Fsrc, the domains Dsrc and Ddest select the translator. If a single translator is visible that translates from Dsrc to Ddest, then that translator is used. If multiple translators are visible, then the user must disambiguate in the specifications.
Default interactions are specified by use clauses at the package level. If a use clause appears prior to a package definition and references an interaction, then the interaction becomes the default for all facets, packages, domains, and components defined in the package. The default is overridden by using a specific interaction in conjunction with definitions in the package. Defaults for all declarations are defined at the outermost working package level.
Translators are applied to facet parameters when one facet instantiates another using the attribute notation. The translator decorates the actual parameter. The specific notation is:
label: name(p't,...);
where name is the instantiated facet name, p is an actual parameter instantiating the associated formal parameter, and t is the translator function used to move information from the included facet domain to the including facet domain. It is possible for t to have parameters, but all parameters must be specified when the translator is used.
Whether the formal parameter associated with p is an input or output parameter, instantiating it with p’t asserts that the application of t to p must result in a value compatible with constraints on the formal parameter.
Functors are simply functions whose domain and range include facets. Thus, functor application is function application. Specifically:
name(p0,p1,...,F)
evaluates to the application of functor name to a facet F. The facet is a required parameter. Other specified parameters, p0,..., pk, precede the facet parameter in the argument list. This is done to allow currying to specialize functors.
Combinators are also functions whose domain and range include facets. The only distinction from functors is that the combinator must include two facets. Like functor application, combinator application is identical to function application. Specifically:
name(p0,p1,...,F1,F2)
elaborates to the application of the combinator name to facets F1 and F2. The facets are required parameters. Other specified parameters, p0,..., pk, precede the facets parameters in the parameter list. Again, this is done to allow currying to specialize combinators.
Two types of interactions exist in the base Rosetta system. Semi-lattice interactions are defined between interconnected domains in the domain semi-lattice. They define the abstraction and concretization functions alpha and gamma that allow moving a specification in the semi-lattice. In addition, semi-lattice interactions are created whenever a new domain is added.
Ad hoc interactions are defined by hand when an interaction between domains is desired. These interactions provide mechanisms for moving directly between domains when it is more natural to be moving up and down the semi-lattice. User-defined ad hoc interactions may also define interactions between domains when default interactions do not suffice.
Whenever a domain is included in the domain semi-lattice, an interaction exists between it and its supertype and subtypes. The interaction between a domain and its supertype is given the name alpha and represents an abstraction of the domain into its supertype. Specifically, alpha(f) moves f from its current domain to its immediate supertype domain. The interaction between a domain and its subtypes is given the name gamma and represents a concretization of the domain into one of its subtypes. Specifically, gamma(f) moves f from its current domain to one of its subtypes, as determined by ascription or context.
Instances of both alpha and gamma are calculated from the extension that refines a domain into its subtype. In Chapter 12, the where clause is defined in domains to specify how a facet in a domain is elaborated. Specifically, given f::D, the where clauses define how D is extended with elements from f to define a facet. Because a domain extends its supertype like a facet extends its type, the where clauses also define the instance of gamma needed to concretize a specification, moving it from its type to one of its subtypes.
The inverse of the transformation defined by with clauses defines the instance of alpha used to abstract a specification, moving it from its type to its supertype. If a specification is concretized using gamma and abstracted using the related alpha, the result is the original facet in the abstract domain:
alpha(gamma(f)) == f
Unfortunately, the same relationship does not hold when abstracting a specification. If the original specification uses items defined in the concrete domain, those definitions will be lost in the abstraction and cannot be regenerated. When applying gamma, we know exactly what information is added to a specification. When defining a specification in the concrete domain, we cannot make the same claim. A specific case of this occurs when applying alpha and gamma to move between discrete_time and infinite_state. If specific time values are used in a discrete_time specification, such as:
x@(t+1) = f(x)
there is no way to preserve the time value in the infinite_state specification. The information is necessarily lost. However, if the discrete_time specification uses next rather than a specific time reference, applying alpha results in a specification than can be concretized:
x@next(t) = f(x)
The next function exists in infinite_state, but simply at a more abstract level.
The implication is that while gamma can always be applied to make a specification more concrete, alpha is restricted. Specifically, if a specification uses items defined in the concrete domain, alpha may not produce the desired abstraction. If specification reuse composition is a goal, such relationships must be taken into consideration.
Ad hoc interactions exist between many domains that are not related by a subtype relationship. For example, moving between the frequency and continuous_ time domains or the finite_state and discrete_time domains requires information beyond that defined by semi-lattice extensions. Unlike those generated automatically by adding domains to the semi-lattice, ad hoc interactions are always written by hand.
Example 15.4. Using alpha and gamma for Moving within the Semi-lattice
Using alpha and gamma interactions to move between domains has great utility when composing specifications. For example, in activity-based power modeling, power consumption is defined over state change. When a system’s state changes, power consumption is estimated based on the type of state change. Thus, it makes good sense to define power models in the state_based domain:
facet power [Ti,To::type] (x:: input Ti; y:: output To; leakage:: design real; change:: design real)::state_based is export p; p::real; begin p' = p + leakage + if event(y) then change else 0 end if; end facet power;
As a system specification involving the power facet is refined, the specifics of state may change substantially. Ideally, the power model should be refined along with the system model by default. Thus, if we write a model in the discrete_time domain, then we could refine the power model to exist in the discrete_time domain:
power_dt[Ti,To::type](x:: input Ti; z:: output To; l,c:: design real) :: state_based is gamma(gamma(power(x,z,l,c)));
Similarly, alpha can move a specification up in the domain semi-lattice. Looking at power aware modeling again, it may be more desirable to abstract the system model to the state_based domain for evaluation. In the same manner that power moved down, system can move up:
system_sb(x:: input bit; z:: output bit) :: state_based is alpha(alpha(system(x,z)));
An excellent example of an ad hoc interaction occurs between the continuous_time and frequency domains. Mathematically, this interaction defines the Fourier transform and inverse Fourier transform moving between frequency and time. This interaction is predefined; named fourier_transform, it defines fourier and inverse_fourier morphisms. The signature of this interaction has the following form:
interaction fourier() between continuous_time and frequency is export all; begin begin translators end translators; begin functors fourier() from continuous_time to frequency; inverse_fourier() from frequency to continuous_time; end functors; begin combinators end combinators; end interaction fourier;
Only functors are defined in this interaction, allowing a user to specify the Fourier and inverse Fourier equivalents of a facet. However, it is not possible to interconnect or compose continuous_time and frequency domains using pre-existing functions. Specifiers are of course allowed to write their own translators and combinators if desired.
Although an interaction between state_based and static domains is generated automatically by the semi-lattice construction, defining the interaction by hand provides useful insight. The ad hoc definition in Figure 15.1 defines the translators, functors, and combinators necessary to combine state_based and static facets.
Example 15.1. An interaction defining the relationship between the state_based and domains.
interaction static_state_based() between static and state_based is export all; begin begin translators alphaT[T::type]() from x::T in state_based to T in static is if is_tick_operation(x) then operand(x) else x end if; gammaT[T::type]() from x::T in static to T in state_based is << tick_operation 'x' 'at(s) >> end translators; begin functors alpha() from state_based to static; gamma() from static to state_based; end functors begin combinators alphaC() from x::state_based and y::static to static is alpha(x) + y; gammaC() from x::static and y::state_based to state_based is gamma(x) + y; end combinators; end interaction static_state_based;
Two translators facilitate moving information through parameters between domains. The alphaT translator moves information from state_based to static while gammaT moves information from static to state_based. Moving from static to state_based adds the ’at(s) notation, to add dereferencing to the static parameter. Moving from state_based to static simply replicates the actual parameter.
Two combinators compose specifications by moving one to a higher or lower abstraction level. The alphaC combinator moves its state_based argument into the static domain and performs composition. Conversely, the gammaC combinator moves its static argument into the state_based domain and performs composition.
Finally, the two functors alpha and gamma move specifications between domains. Specifically, alpha moves a specification from the more concrete domain, state_based, to the more abstract domain, static. The functor gamma performs the inverse, moving specifications from static to state_based. The details of these functors are omitted, as they will be generated automatically by the construction of the semi-lattice.
A common mechanism for defining new interactions is to compose elements from existing interactions. Because functors and combinators are simply functions, it is easy to define new interactions by composing interaction elements using function composition. Figure 15.2 defines such an interaction between finite_state and discrete_time domains. Such an interaction would be useful when taking a finite state machine and moving to discrete time for simulation or integration with a larger system.
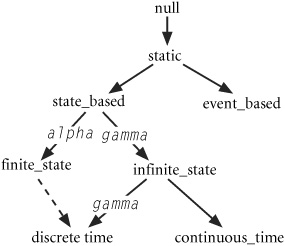
Figure 15.2. The domain semi-lattice before and after creation of a finite_state to discrete_time interaction.
Moving between finite_state and discrete_time is a simple matter of applying multiple alpha and gamma functors. Defining the interaction simply institutionalizes the interaction and increases readability. Each functor and combinator is defined by composing existing functions using the function composition operator.
The finite_state_discrete_time interaction defines two functors and three combinators (Figure 15.3). The functors are defined by composing alpha and gamma functions from interactions defining paths between domains in the semi-lattice. Both functors move a specification from one domain to the other defined in the interaction.
Example 15.3. Interaction between finite_state and discrete_time, constructed by composing interaction components.
use state_based_finite_state(), state_based_infinite_state(), infinite_state_discrete_time(); interaction finite_state_discrete_time() between finite_state and discrete_time is begin begin translators end translators; begin functors finite_state_to_discrete_time() from finite_state to discrete_time is infinite_state_discrete_time.gamma. state_based_infinite_state.gamma. state_based_finite_state.alpha; discrete_time_to_finite_state() from discrete_time to finite_state is state_based_finite_state.gamma. state_based_infinite_state.alpha. infinite_state_discrete_time.alpha; end functors; begin combinators finite_stateC() from x::finite_state and y::discrete_time to finite_state is x * discrete_time_to_finite_state(y); discrete_timeC() from x::finite_state and y::discrete_time to discrete_time is finite_state_to_discrete_time(x) * y; state_basedC() from x::finite_state and y::discrete_time to state_based is state_based_finite_state.alpha(x) * (state_based_infinite_state.alpha . infinite_state_discrete_time)(y) end combinators; end interaction finite_state_discrete_time;
The first two combinators are similar to the functors in that they define moving one specification to the other’s domain and performing a facet product. The functors defined in the interaction are used to define the combinator. The third combinator is more interesting, as it moves both specifications into the state_based domain and performs composition there. In effect, both specifications are moved to a common abstract domain and are composed. This combinator might be used to perform analysis or to lift results from a concrete specification into a more abstract context.
