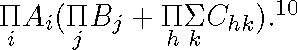Chapter Four

The Löwenheim Normal Form

4.1 THE LÖWENHEIM NORMAL FORM OF AN EQUATION

4.1.1 As I stated at the beginning of the previous chapter, the first part of Löwenheim's proof consists in showing that every equation is equivalent to an equation that has a certain normal form. Löwenheim considers an equation to be in normal form if it has the form , where F is a quantifierfree formula, represents a possibly empty string of existential quantifiers (either type Σ or ) and II represents a possibly empty string of universal quantifiers (as a special case, F = 0 is in normal form).

Löwenheim assumes in “Über Möglichkeiten” that all equations are in the form A = 0;¹ and so what he actually proves is that every equation in this form can be reduced to another equivalent equation in normal form. Since both the initial equation and its equivalent in normal form are made equal to zero, what is to be proved, expressed in our terms, is that for every formula A there exists a formula such that

(1) is in prenex form and every existential quantifier (either type or ) precedes every universal quantifier; and

(2) A and are logically equivalent.

4.1.2 Löwenheim's procedure for reducing a given formula to a logically equivalent formula in normal form has two stages. First, he transforms the original formula into a logically equivalent one in which the quantifiers are partially grouped in such a way that no existential quantifier occurs in the scope of a universal quantifier. Then, ifthe resulting formula is not yet in prenex form, he obtains a prenex formula logically equivalent to it.

I will quote the extracts in which Löwenheim describes the two transformations separately, and I will present a brief summary immediately after each in order to clarify the general structure of the argument. I will give a detailed analysis in the subsequent section.

4.1.3 Löwenheim describes the first transformation as follows:

For the proof we think of the equation as brought into zero form. We prove first that every first-order equation can be brought into a certain normal form, which is given on page ... under (3) [[IIF = 0]]. First we try to see to it that no II or Σ ever occurs under a (simple or multiple) II. If we assume that a productand contains at least one II or Σ, we can distinguish four cases:

1. The productand is a · product. We can eliminate such a product by using the formula

(In particular, e.g., we have )

2. The productand is a II product (say, where the Aik are functions of relative coefficients). Then II can be extricated from the productand by means of the formula

3. The productand is a + sum, hence something like, say,

A + B + C + ... not ad inf.

Here we distinguish two subcases:

(a) One or several of the A, B,... are (· or II) products. This case can be reduced to Case 1 or Case 2 by means of what we may call “adding out” with the help of the formula a + bc = (a + b)(a + c).²

(b) None of the A, B,... is a product. Indeed, a + sum cannot be one if the A, B,... are really the last summands into which the productand can be decomposed without the use of Σ. Therefore each of the A, B,... is either a (negated or unnegated) relative coefficient or a Σ. If all of these summands are relative coefficients, we have already reached our goal; but if, for example,

then the productand can be written in the form

which reduces this case to Case 4.

4. The productand is a Σ sum. Then our task consists in transforming the into a , that is, in multiplying out the product. This is done by means of the formula

[...]

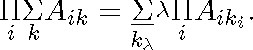
In case a multiple Σ is preceded by a multiple II our formula must be generalized as follows:

By means of the procedure described in Cases 1–4 every Σ and II can be removed from the productand step by step.⁴ In this process it may very well happen that the transformation given in Case 4 must be applied several times in succession, and we still want to indicate how this is done:

(“Über Möglichkeiten,” pp. 450–452 (235–236))

Löwenheim's purpose is to prove that every formula is logically equivalent to another that does not have a quantifier in the scope of a universal quantifier. To understand how to avoid a universal quantifier occurring in the scope of another, we need the distinction between simple and multiple quantifier that we explained in subsection 2.5.2 of chapter 2. For example, in

there is a quantifier in the scope of another one, but not in the logically equivalent formulas

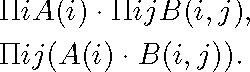
The first of these has two quantifiers, one simple and one multiple, and the second has a single multiple quantifier. In this way, these two formulas are logically equivalent to the first and, stated in Löwenheim's terms, have no quantifier in the scope of another quantifier.

Löwenheim calls the scope of a universal quantifier the productand.⁵ For example, IIjA(i,j) is not a productand of IIijA(i,j), because a multiple quantifier is considered as a single quantifier, but it is a productand of IIiIIjA(i,j)). The productands of a formula are the scopes of its universal quantifiers. Thus, A(i) and B(i,j) are productands (but not factors) of IIiA(i) · IIijB(i,j).

According to Löwenheim, cases 1–4 describe a procedure that allows the elimination of quantifiers from any productand in a finite number of steps. These cases correspond to four possible forms of the productand.⁶ Observe that the productand cannot be a relativecoefficient (since he is supposing that it has at least one quantifier), or a negated complex formula, because he is assuming without any warning that negation symbols are distributed in such a way that they affect only relative coefficients.⁷

Once Löwenheim has shown how to eliminate the quantifiers occurring in any productand, he considers that he has solved the problem of finding a formula without quantifiers in the scope of a universal quantifier logically equivalent to any given formula. He does not explain how to find the formula, but this is a trivial matter. If A is any formula, we can obtain a formula logically equivalent to A without quantifiers in the scope of a universal quantifier in this way: if IIi is the first quantifier on the left that has another quantifier in its scope P, then we replace the subformula IIiP of A by a logically equivalent formula in which no quantifier occurs in the scope of IIi; if some universal quantifier of the resulting formula has a quantifier in its scope, we proceed as in the case of A; if not, has the required properties and therefore, we are done. This is the end of the first stage.

4.1.4 All that remains now in order to obtain the normal form is to reduce the formula resulting from the previous transformation to a logically equivalent formula in prenex form. Löwenheim explains how to do so, as follows:

After the productands have all been freed from Σ and II, it remains only to remove all parentheses that do not immediately follow a Σ or II and to multiply out the products of the Σ. This is done by means of the formula

and similarly in the case of multiple sums.

In exactly the same way a can also be multiplied by another, or by a Σ, and likewise for multiple sums.The final result is an equation of the form

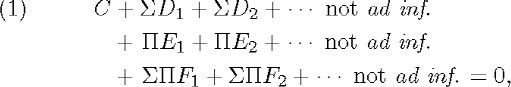
where the sums and products will in general be multiple ones and the C, Dv, Ev, and Fv are identical functions of relative coefficients without or II. In our example of page ::: we obtain, bymeans of the transformations sketched,

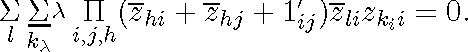
Now in (1), to begin with, we can see to it that exactly the same summation indices occur under each of the Σ by merely adding any missing ones (since ). To the terms without Σ we can simply add a Σ (since ).Thereupon we can combine all Σ into a single Σ (since )). We obtain an equation of the following form:

or, added out according to the formula

ΣII(F0 + F1 + F2 + ··· not ad inf.) = 0,

or, for short,

(“Über Möglichkeiten,” p. 453 (237))

In the following section I will comment on the elimination of the parentheses that do not immediately follow or II. For the moment it is enough to observe that the result of applying all the transformations mentioned so far (including the elimination of the parentheses) mustbe a disjunction of formulas in normal form, that is, a formula of the form

where C, D1,..., Dn, E1,..., Em, F1,..., Fr are formulas without quantifiers and the existential quantifiers may be of the type .

Assuming that we have obtained a formula of this form, all that remains, stated informally, is to move all the inner quantifiers in the appropriate order to the front of the formula. According to Löwenheim, the only equations required to perform this task (the only ones he mentions explicitly) are

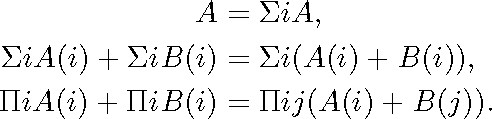
Interestingly, Löwenheim does not say which equations should be applied in the case of the quantifier .

In these equations certain evident restrictions are assumed: that the variable i does not occur in A, that the variable j does not occur either in A(i) or in B(i); and that B(j) is the substitution of i by j in B(i). Neither Schröder nor Löwenheim mention these details, but in practice their application of the equalities is always correct. To make my commentary rather more fluid, and bearing in mind the fact that the restrictions are obvious, I take the liberty of omitting them from what follows.

4.2 COMMENTS ON LÖWENHEIM'S METHOD

4.2.1 First stage

4.2.1.1 I will start by analyzing subcase (a) in the third case of the process of elimination of the quantifiers from the scope of a II. As we have seen, Löwenheim says that if some ) is a product of type · or of type II, A₀ + ... + A_n can be reduced to a formula of the form A · B or the form IIkA(k) by means of what he calls adding out (Ausaddieren) with the help of

It is plain that Löwenheim should have distinguished between the two kinds of products, but this detail is of little importance. I will explain first the meaning of Ausaddieren.

At various points in the proof, Löwenheim uses the terms ausaddieren and ausmultiplizieren, in either noun or verb form. Literally, these terms refer to performing the sums and the products in question. They can be translated by to add out and to multiply out, respectively, but neither the literal meaning nor the translation helps us to understand what Löwenheim means because, for example, it is not clear in what way performing the sums in question in A₀ + ... + A_n helps us to obtain a formula of the form IIkA(k). Therefore, for the moment we are best advised to ignore the literal meaning of the terms and to analyze the contexts in which Löwenheim uses them.

Except in the case we are considering, Löwenheim always mentions the equation that allows us to perform the transformation. According to him, we perform an Ausaddieren when we apply

from left to right, and an Ausmultiplizieren when we apply

from left to right. In addition, when he introduces the formula

he states: “our task consists in transforming the IIΣ into a ΣII, that is, in multiplying out the product” (this is done by means of the said formula) (“Über Möglichkeiten,” p. 451 (236)).

The equation (4.3) clarifies all we need to know to proceed in the case we are considering, but the meaning of these terms becomes clearer if we observe the two cases of Ausmultiplizieren. Löwenheim uses this term to refer not to a particular equation, but to a certain type of transformation that is performed by applying different equations according to the particular cases. From the algebraic perspective — the appropriate perspective in these cases — what the last two equations have in common is that in both we go from multiplying sums to adding products (understanding both Σ and + as sums, and both II and · as products). Generalizing, we can say that ausmultiplizieren consists in transforming a product of sums into an equivalent sum of products. For its part, ausaddieren consists in transforming a sum of products into a product of sums. As can be seen, the truth value of the formula that results from performing an Ausaddieren (or an Ausmultiplizieren) is calculated by performing first the sums (or the products). This is the idea that the name suggests.

According to this interpretation, each time we apply the equation (4.1) we are carrying out an Ausaddieren. Löwenheim's explanation of how to perform the reduction suggests that he is reserving these names for the transformations in which quantifiers intervene,⁸ but there is no way of establishing this, and in any case it is of no great importance. Leaving this question aside, we should note that when Löwenheim talks of applying (4.1) he should be understood as referring to a type of transformation as well. In present-day terminology, this transformation consists in going from a disjunction of conjunctions to a conjunction of disjunctions. Strictly speaking, this step may require not only the application of (4.1), but also the application of the commutative property of the disjunction.

Translating Ausaddieren as “distributing the sum” and Ausmultiplizieren as “distributing the product” is less literal, but it gives a better idea of the nature of the transformations and remains close to the algebraic spirit. In fact, it would be in agreement with Schröder's terminology, which does not coincide exactly with Löwenheim's. According to Schröder, ausmultiplizieren consists in applying the equation

(in the sense I have just explained). For example, going from the formula

to the formula

is to multiply out (ausmultiplizieren) polynomials (Vorlesungen I, pp. 284 and 292). Schröder does not give a specific name to the transformation consisting in the application of equation (4.1) (which he comments on together with the previous one). To my knowledge, Schröder does not use the term ausaddieren. He calls equations (4.2) and (4.3) “distributive laws” because he considers them to be generalizations of (4.1) and (4.4), respectively.

Almost all the transformations that Löwenheim refers to are thus clarified. I believe that, with certain inaccuracies typical of his times, Löwenheim gives all the information necessary for performing the reduction of this case to the previous ones. The only criticism thatcould be made is that the two types of product are treated together. In all likelihood, Löwenheim's reason for joining them is that in the logic of relatives this reduction (whatever name it is given) is seen as the transition from sums to products. If we incorporate all the above clarifications and distinguish the two types of product, the result is the following:

(a₁) if some Am is a product of type ·, the sum is reduced to a product of the same type by means of (4.1) (and the commutative property of the sum); and

(a₂) if no Am is a product of type · but some Am is a product of type II, the sum is reduced to a product of the same type by means of (4.2).

As can be seen, (4.2) does not suffice to reduce the disjunction to a generalization, but Löwenheim is aware of this. The point is that his procedure for moving the quantifiers of a formula is different from the one we use today. I will return to this issue in subsection 4.3.4.

4.2.1.2 After explaining the meaning of the equation

Löwenheim generalizes it to the case of multiple quantifiers in this way:

He notes in addition that, in the process of eliminating the quantifiers from the scope of a II, it may be necessary to apply (4.5) repeatedly, and he shows how to do so as follows:

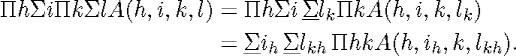
The first point to observe in Löwenheim's example is that he applies not only (4.5), but the equation

It is easy to check that this equation is logically valid.⁹ The proof is essentially the same as the proof of (4.5) and also depends on the axiom of choice.

Second, there is nothing in the way that the existential quantifiers are eliminated from the scope of a II that necessitates a successive application of (4.5) (or of (4.5) and (4.6), as we have just seen).

Löwenheim's generalization of (4.5) is enough for his purposes. In fact, the following equation, which is simpler, suffices:

Löwenheim generalizes equation (4.5) due to the distinction between simple and multiple quantifiers. From his point of view, (4.7)is not, strictly speaking, applicable to the case of a multiple existential quantifier like, for example, . If this distinction is not made, the application of (4.7) a finite number of times suffices to eliminate the existential quantifiers from the scope of the universal quantifiers. Indeed, this is how we would proceed today.

Only when a occurs in the scope of a II is it necessary to apply (4.6), but if the existential quantifiers are eliminated from the scope of a II in the appropriate order this situation never arises. Löwenheim needs to apply (4.6) in the case of ,(h,i,k,l) because he proceeds from right to left instead of from left to right (i.e., he eliminates from the scope of IIk before eliminating i from that of IIh). Nevertheless, the order that he follows in his example is acceptable in the sense that equations (4.5) and (4.6) suffice to prove that every prenex formula is logically equivalent to a formula in normal form. The proof is by induction on the number of universal quantifiers that have in their scope an existential quantifier (). If this number is zero, the formula is already in normal form. If it is n + 1, we turn to the universal quantifier furthest to the right which has a in its scope. Applying (4.5) and (4.6) a finite number of times, we can eliminate both kinds of existential quantifiers from the scope of the II. The result is a formula that has n universal quantifiers with an existential quantifier in their scope and, by the induction hypothesis,is logically equivalent to a formula in normal form.

4.2.2 Second stage

4.2.2.1 Once we have obtained a formula with no quantifiers in the scope of a universal quantifier, all that remains is to obtain a prenex form for formulas of this kind. According to Löwenheim, the first steps to take in this direction are “to remove the parentheses that do not immediately follow a Σ or II and to multiply out the products of the Σ” by applying

I will explain what elimination of the parenthesis means with an example that will also allow us to detect some small errors in Löwenheim's argument. In this subsection I will write the formulas in the notation that Löwenheim used because now it is important that no parentheses other than those of the original notation should occur.

Let us consider the · product

¹⁰

After eliminating the quantifiers from the scope of a II, we obtain the formula

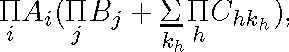
in which there occur parentheses that do not immediately follow a quantifier. To see how these parentheses are eliminated it is enough to observe that this formula fits the schema a(b + c). If we thinkin arithmetical terms, it is plain that eliminating parentheses means applying

If we apply this equation to our example, we obtain

Generalizing, the elimination of parentheses, put in our terms, consists in giving the propositional structure of the formula the disjunctive normal form. In arithmetical terms, this transformation, like (4.8), is a distribution of products. We thus reach the dual situation of what we saw in subsection 4.2.1. The fact that here Löwenheim clearly distinguishes between the elimination of parentheses and the application of (4.8) supports the idea that he only uses the verbs ausaddieren and ausmultiplizieren in the cases of quantification.

To return to the example, if, as Löwenheim says, we apply to the right-hand summand in (4.9) an equation for the analogous to (4.8) (i.e., an equation that permits to move the · to the front of a product), we obtain

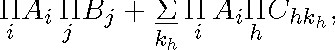
which still does not have the form that Löwenheim foresees. To obtain a disjunction of formulas in normal form we need to move the universal quantifiers to the front of the products where they occur.

It is surprising that Löwenheim should forget this step, because previously he has distributed the universal quantifiers in the conjunction, and if we want to obtain a formula which has all the quantifiers at the beginning at some point we will have to retrace our steps. In addition, this transformation is necessary even in his own example. According to him, the result of applying all the transformations mentioned so far to

is

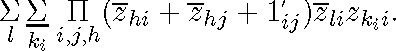
Evidently, Löwenheim did not follow his method to obtain the normal form of (4.10); if he had, the result would have been

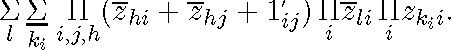
To see why, we first observe that

is the only productand in (4.10) in which a Σ occurs. If we follow Löwenheim's method for eliminating the quantifiers occurring in any productand, we will obtain

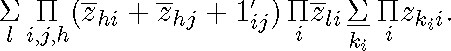
(Recall that Löwenheim removes the vacuously quantified variables, as his own example shows: .)Now, the result of “multiplying out the products of the Σ” is

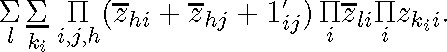
There is still another difficulty that precludes obtaining the disjunction of formulas in normal form. Let us suppose, for example, that the formula we wish to transform is

After eliminating the existential quantifier from the scope of the II, we obtain

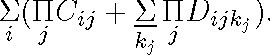
According to Löwenheim, we should now obtain a disjunction of formulas in normal form by eliminating the parentheses and moving the existential quantifiers to the front of the conjunction. It is clear, however, that these transformations cannot be applied to this formula (the parentheses immediately follow Σ). In order to obtain a disjunction of the form mentioned by Löwenheim, we must either obtain a prenex form of the above formula or apply

It does not matter which strategy we adopt, because in either case we will need to apply some equivalence that Löwenheim does not mention in this context. I suppose that in this case he would follow the first strategy, since the next step consists precisely in obtaining the prenex form of the whole disjunction of formulas in normal form.

4.2.2.2 After obtaining a sum of formulas in normal form, Löwenheim says that it only remains to move all the inner quantifiers in the appropriate order to the front of the formula. To move the quantifiers, he uses the equivalences

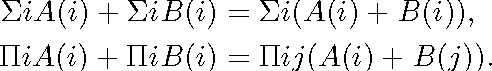
Obviously, these equations can only be applied when the same quantifier occurs in both members of the sum. Löwenheim is aware of this detail and notices that it will always be possible to apply the first of the two above equations, since we can add the quantifiers that are required by applying the equivalence A = ΣiA (where i does not occur in A). Löwenheim forgets to mention the equivalence A = IIiA, which is what allows us to add the required universal quantifiers. Moreover, if the quantifiers are not in the appropriate order, as for example in , we will have to re-order them.

The disadvantage of using these equivalences to move quantifiers is that on occasion it is necessary to introduce universal quantifiers which have to be removed at the end of the process to avoid the final formula having vacuously quantified variables. Let us consider, for example, the formula IIiA(i)+B, and let us suppose that i and j do not occur in B. To move the quantifier following Löwenheim's procedure, we first have to add the quantifier that is lacking: IIiA(i)+IIiB; now, if we apply the corresponding equation, we obtain IIij(A(i) + B), in which the variable j is quantified vacuously.

Finally, I will make a short comment on the laws that are used to move the , or, put in the terms of the logic of relatives, on how to add and multiply the . On this point, Löwenheim only says that they are multiplied in the same way as the Σ. It is understandable that he gives no more explanations because, as I said in subsection 3.3.4 of chapter 3, he thinks of as a multiple quantifier, and with multiple quantifiers we operate essentially in the same way as with simple quantifiers. It is difficult to know how Löwenheim would have formulated the equations for the case of the ; possibly, like this:

Perhaps he would have written i instead of , but both options pose essentially the same problems when the equivalences are applied in combination with the others. Let us consider, for example, the formula

If we move ki and then apply the equivalence (4.2), we obtain

which is misleading, because it is not clear whether the terms generated by kj are bounded or not by k_i. The difficulty is essentially the same if we write ¸ instead of k_i.

It seems to me that Löwenheim would move the guided more by his comprehension of the meaning of the symbols than by the literal application of any equation. In any case, most of the problems related to the laws needed to move the disappear if in the starting formula we introduce the alphabetical changes required to ensure that no variable is quantified more than once and no variable is both free and quantified.

4.3 CONCLUSIONS

4.3.1 Löwenheim aims to prove that every formula is logically equivalent to a formula in normal form and to offer a procedure for obtaining the normal form of any given formula.¹¹ I will start by highlighting certain characteristics of the procedure that Löwenheim follows, and will then make an evaluation of it.

One of the most striking features of the way in which Löwenheim obtains the normal form is that, in general terms, the order in which he proceeds is the opposite of the one we follow today. First he moves the existential quantifiers in front of the universal ones, and then obtains the prenex form. This way of obtaining the normal form introduces numerous, totally unnecessary complications, one of which is the toing and froing of universal quantifiers whose scope is a conjunction in which one or more quantifiers occur. It may be that in the first part of the process these quantifiers have to be distributed in the conjunction (thus undoing something that has already been presented to us as done) and later the reverse step has to be taken (something which, it appears, Löwenheim forgets to do).

The most unfortunate consequence of the order that Löwenheim follows is that the prenex form is not obtained inside a standard first-order language, because the formula that results from changing theorder of the quantifiers will in general contain quantified fleeing indices. Thus, in order to obtain the prenex form we need equivalences that tell us how to deal with these expressions and how to resolve the syntactic difficulties that they present. This is not a particular problem for Löwenheim, since he considers as a normal multiple quantifier. He therefore thinks that, for , essentially the same equivalences are valid as for Σ, and, in addition, that the syntactic aspects merit little or no attention inside the logic of relatives.

Leaving aside considerations of the elegance of the method for obtaining the normal form (a secondary issue when one is breaking new ground), the only criticism that in my opinion can be justifiably leveled at Löwenheim is that he is not particularly careful (even considering the standards of rigor of his times). The first stage of his procedure is essentially correct and shows, as I said in chapter 2, a valuable intuition on the recursive structure of a formal language. I do not mean that Löwenheim understands it well, and indeed certain details in his presentation show that he does not. Nonetheless, he deserves credit, because what he achieves is substantially more than one might expect, considering that he has no precise definition of a formula. Obtaining the prenex form (the second stage) presents more problems, but it would be unfair to criticize him for this. In the first place, his exposition contains the main steps for obtaining the prenex form (and there is no doubt that he knew how to do it in practice). Second, in Löwenheim's time the general understanding of the recursive structure of a formal language was not sufficient for him to accurately foresee the logical form of the formula resulting from the application of a recursive procedure to any formula. It is hardly surprising that Löwenheim overlooked some of the equivalences needed to obtain a disjunction of formulas in normal form.

In summary, perhaps it cannot be said strictly that Löwenheim manages to provide a procedure for obtaining the normal form of any formula. What we can say is that his recursive procedure for eliminating the quantifiers from a productand is basically correct and that, considering the two stages together, his exposition contains the basic indications for obtaining the normal form of any formula. Unfortunately, this part of Löwenheim's proof has passed completely unnoticed. ¹² Indeed, there are reasons for thinking that it has not been understood, or at least has not been studied. This is possibly the onlyexplanation for the fact that van Heijenoort's unfortunate comments on the productands are preserved in the successive editions of From Frege, the fact that the two evident errata that I have mentioned are not pointed out, and above all the surprising fact that no scholar has made even a passing reference to the way in which Löwenheim obtains the normal form.

4.3.2 Löwenheim does not speak of the equivalence of the initial equation and the resulting equation in normal form, and it is natural that he should not do so. All the steps that constitute the process of obtaining the normal form consist in replacing subformulas of the initial formula by others that are “equal” (or, more accurately, logically equivalent). In this way, the equivalence of the two formulas is considered to be obvious, assuming that the equations used in the process are logically valid. Indeed, this is the form in which this type of proof is frequently presented today.

We should also make a comment on the equations that Löwenheim uses. He always takes their validity for granted, and does not attempt to prove any of them. This is evident and would not be worth mentioning were it not for the fact that his clarifications of equation (4.5), which allows us to put the existential quantifiers in front of the universals, have been misinterpreted. Van Heijenoort states:

Since the formula [[IIiA(i, ki)]] is again of finite length, Löwenheim has taken, according to Skolem, a detour through the transfinite. During this detour an argument that justifies the equivalence (I), or (II), in the case of the finite domain is—unwarrantedly—extended to the case of an infinite domain. (From Frege, p. 230)

(I) is equation (4.5), and (II) is its version in terms of Skolem functions. It is doubtful whether Skolem's words have the meaning that van Heijenoort attributes to them, but I am not going to consider that issue here. As far as the proof of (4.5) is concerned, van Heijenoort most probably takes the expansions that Löwenheim uses to clarify the meaning of the equation as an informal proof of it. But, as I argued in the previous chapter, Löwenheim does not use expansions with the intention of proving something. His purpose is to show intuitively that the equations hold. Löwenheim presents examples, but does not offer an argument. Van Heijenoort's criticism could be leveled at Schröder, but not at Löwenheim.

4.3.3 To conclude this chapter, I will schematize and reconstruct

Löwenheim's argument. The purpose of Löwenheim is to prove the following theorem:

Theorem 4.1 Every sentence of a first-order language is logically equivalent to a sentence in normal form.

If F is any sentence, the theorem can be proved by obtaining a prenex formula logically equivalent to F and then applying the equation (4.7) in order to eliminate the existential quantifiers of the scope of the universal ones. As we have seen, Löwenheim's proof is different. His argument can be split into four parts (although the second one is only implicit); each one of them can be read as the proof of a lemma. The theorem is a trivial consequence of those lemmas.

To simplify the exposition, I will say that a formula F is partially normalized if

(1) no existential quantifier of F occurs in the scope of a universal one; and

(2) if IIh occurs in the scope of IIi, both IIh and IIi belong to the same string of universal quantifiers.

For example, the formula IIi(A·IIhB) is not partially normalized, but if no quantifier occurs in A or in B, both IIih(A·B) and IIiA·IIihB are partially normalized.

Lemma 4.2 Every sentence of the form IIi₁...i_nP can be reduced to a partially normalized logically equivalent sentence F.

I will now reproduce Löwenheim's proof of this lemma in order to make its recursive structure evident. I will introduce the clarifications explained so far. The proof is by recursion on the degree of IIi₁...i_nP, that is, on the number of logical symbols of P. Löwenheim cannot fully grasp the recursive structure, but he has an intuitive idea of how it might work.

If no quantifier occurs in P, we are done. Let us assume that P contains at least one quantifier. Since the negation symbols affect only relative coefficients, only four cases are distinguished:

(1) If P is a product of the form A · B, the universal quantifiers of IIi₁...i_nP can be distributed by using the equation

(2) If P is a product of the form IIkA, we apply

where the formula on the right is of degree less than the one on the left.

(3) If P is a sum such as A₀ + ... + A_n, where for each m ≤ n, Am is not a sum, then three subcases are distinguished:

(a) Some A_m is a product of type ·. This case is reduced to (1) by transforming the sum into a product of type · with the help of (4.1) (and the commutative property of the sum).

(b) No A_m is a product of type · but some A_m is a product of type II. This case is reduced to (2) by transforming the sum into a II product by means of (4.2) (and the required introductions).

(c) No is a product (of type · or II), but some A_m is a sum of the form . This case is reduced to (4) by means of

Löwenheim also mentions the possibility that all the Am are negated or unnegated relative coefficients. This case cannot be so if in the productand (A₁ +...+A_n, in this case) a quantifier occurs (as he assumes at the beginning). Nevertheless, his remark shows that he is thinking of a step-by-step reduction, that is, of a recursive procedure.

(4) If P is an existential formula such as , we apply:

thus getting a formula of lower degree. This concludes the proof.

Lemma 4.3 Every sentence is logically equivalent to a partially normalized sentence.

This lemma is implicitly regarded by Löwenheim as an immediate consequence of the previous one, and together they constitute what at the beginning of this chapter I called “the first stage” of Löwenheim's argument.

Lemma 4.4 Every partially normalized sentence is logically equivalent to a sum of sentences in normal form.

In my opinion, the fragment of Löwenheim's proof corresponding to this lemma is the weakest part of his argument. He seems to think that the formula resulting from introducing the changes mentioned so far in a given sentence will be a Boolean combination of partially normalized formulas. If this were true, we could just say that Löwenheim forgets to move the universal quantifiers of a conjunction to the front, but unfortunately we do not obtain the Boolean combination described. I think this mistake is comprehensible, since the only way to ensure that the formula resulting from a series of transformations has a determinate form is to carry out a rigorous proof by recursion, and Löwenheim does not have this resource at his disposal.

To prove this lemma and the next one, we need to move the quantifiers of type . As mentioned in subsection 4.2.4, this task poses no problem if in the starting formula we have introduced the alphabetical changes required to ensure that no variable is quantified more than once and no variable is both free and quantified.

Lemma 4.5 Every sum of sentences in normal form is logically equivalent to a sentence in normal form.

This lemma is trivial and Löwenheim's proof of it is correct.

¹As we know, this does not imply any loss of generality. The proposition

(which I formulate in the style of the theory of relatives) guarantees that every equation is equivalent to another of the form A = 0:

²[[The translation in From Frege (p. 236) is different:

This case can be reduced to Case 1 or Case 2 by means of the formula a + bc = (a + b)(a + c), that is, by what we may call “adding out.”]]

³[[The equation that should appear is this one:

This erratum has passed unnoticed in the English version included in From Frege.]]

⁴[[Here, the English version of From Frege uses the term “factor” in place of “productand.” This is an erratum, since Löwenheim says Produktand, not Faktor, and the translator retains this distinction throughout the translation. As we will see, Produktand and Faktor are two distinct notions.]]

⁵Schröder refers to the productand as “general factor” (Vorlesungen III, p. 37).

⁶In the version in From Frege, the understanding of this idea is obscured considerably by a comment inserted by the editor. At the beginning of section in which the normal form is obtained (p. 235) we read:

If we assume that a productand contains at least one II or one Σ [[which may be · or +, respectively, as a special case]], we can distinguish four cases.

Van Heijenoort makes no reference to the procedure for obtaining the normal form in his introduction to Löwenheim's paper, and so there is no additional clarification of this comment.

As I have just said, Löwenheim is explaining how to eliminate the quantifiers from a productand and, therefore, assumes that it contains a quantifier, because if this is not the case there is nothing to solve. Löwenheim's statement should be understood literally, and not as van Heijenoort interprets it, because the problem is not whether · or + occur in the productand. In order to show how to eliminate the quantifiers it is necessary to distinguish four cases (depending on the form of the productand), but this is a different question.

⁷Observe also that Löwenheim does not consider the case of the productand being of the form A B, which means that, as I said in chapter 2, he does not include among the basic symbols of the language of the logic of relatives.

⁸The English translation in From Frege suggests the opposite (see note 2 in this chapter).

⁹The coincidence in the subindices should not hide the fact that lk₁...k_nh are lk₁...k_n completely different fleeing indices. If we look at the fleeing indices from the functional viewpoint, this last equation would be

,

where f is an n-place function symbol and g an (n + 1)-place function symbol.

¹⁰According to Schröder's rules for the use of parentheses (Vorlesungen III, p.73), is an abbreviation of

If it were a conjunction, the use of parentheses would be obligatory: . Löwenheim writes both without parentheses, and it is the variables that delimit the scopes. For example, should be considered as a conjunction and

as a formula of the form .

¹¹Löwenheim's method for obtaining a formula in normal form logically equivalent to any given formula A does not determine a unique formula, because, for example, the alphabetical changes required on occasion are not determined. Whenever I speak of the normal form of a formula A, I refer to any formula obtained applying Löwenheim's method to A.

¹²The proof included in the first stage of Löwenheim's procedure for obtaining the normal form may be the first, or one of the first, proofs by recursion in the history of logic, and for that reason I feel that this detail is important.